���185�@�T�̂�����
�T�̂�������y���ق����珇�ɕ��ׂ�ƁA�`�C�a�C�b�C�c�C�d�ł��B
���̂T�̕��ς̏d���́A�R�S�D�Sg�@�ł����B
�܂��A���̂����R�̂������I�Ƃ��A����[1]����[4]�̂��Ƃ��킩��܂����B
�@[1]�@�ł��y���g�����̂Ƃ��A���ς̏d���͂Q�Ug�@�ł����B
�@[2]�@�Q�ԖڂɌy���g�����̂Ƃ��A���ς̏d���́A�Q�Vg�@�ł����B
�@[3]�@�ł��d���g�����̂Ƃ��A���ς̏d���͂S�Tg�@�ł����B
�@[4]�@�R�Ԗڂɏd���g�����̂Ƃ��A���ς̏d���͂R�Wg�@�ł����B
���̖₢�ɓ����Ă��������B
�i�P�j�b�C�c�C�d�̏d�������ꂼ�ꓚ���Ă��������B
�i�Q�j�`�C�a�̏d�������ꂼ�ꓚ���Ă��������B
���̏o�T
��l�̎Z���p�Y��
�͐���
���R������
�t�F���X���w�@���w�Z(2006�N)
��
�`�������ɂ��Љ�܂��`
�E����1
�i�y���l�|���Fhaya�j
���F A=14g, B=23g, C=41g, D=44g, E=50g
�y�������z
�ŏ���4�̏�������
�@�`�{�a�{�b�{�c�{�d���R�S�D�S�~�T���P�V�Q�@�@�@�s1�t
�@�`�{�a�{�b���Q�U�~�R���V�W�@�@�@�@�@�@�@�@�@�@�@�s2�t
�@�`�{�a�{�c���Q�V�~�R���W�P�@�@�@�@�@�@�@�@�@�@�@�s3�t
�@�b�{�c�{�d���S�T�~�R���P�R�T�@�@�@�@�@�@�@�@�@�@�s4�t
�s1�t�́s2�t�Ɓs3�t���
�@�`�{�a�{�Q�b�{�c�{�d���V�W�{�P�R�T���Q�P�R
�@�P�V�Q�{�b���Q�P�R
�@�b���S�P
��̎���
�@�`�{�a���R�V�@�@�@�@�@�@�@�s5�t
�@�`�{�a�{�c���W�P�@�@�@�@�s6�t
�@�S�P�{�c�{�d���P�R�T�@�@�s7�t
�s5�t�Ɓs6�t���A
�@�R�V�{�c���W�P
�@�c���W�P�|�R�V���S�S
����Ɓs7�t����A
�@�S�P�{�S�S�{�d���P�R�T
�@�d���P�R�T�|�S�P�|�S�S���T�O
�`�Ƃa�̒l�ɂ��Ăł����A
3�Ԗڂɏd���g�������a,�b,�d�ƍl����Ɩ����Ȃ��v�Z�ł���
�@�`�{�a���R�V�@
�@�a�{�S�P�{�T�O���R�W�~�R���P�P�S
���A
�@�a���Q�R
�@�`���P�S
�E����2
�i�y���l�|���F�Y���j
�y�z
�i�P�j
�܂���ӂ��s1�t�`�s4�t�����藧�B
ABCDE=172�@�c�s1�t
ABC=78�@�c�s2�t
ABD=81�@�c�s3�t
CDE=135�@�c�s4�t
�s2�t+�s4�t-�s1�t���C=41�@�c�s5�t
�s2�t-�s5�t���AB=37�@�c�s6�t
�s3�t-�s6�t���D=44�@�c�s7�t
�s4�t-�s5�t-�s7�t���E=50
��(C,D,E)=(41,44,50)�@�c�i�����j
�i�Q�j
�R�Ԗڂɏd���g��ADE��BCE�̂ǂ��炩�ł���B
ADE=114�̂Ƃ��A�i�P�j���A=20�A�s6�t���B=17�i�����A��B�ƂȂ��ӂɔ�����j
BCE=114�̂Ƃ��A�i�P�j���B=23�A�s6�t���A=14
��(A,B)=(14,23)�@�c�i�����j
�E����3
�i�y���l�|���F�]�ʔ����j
�`�A�a�A�b�A�c�A�d�̂��ꂼ��̂�����̏d����a�Ab�Ac�Ad�Ae�Ƃ��āA�^��������B
�d���̏���Fa��b��c��d��e
�d���̍��v�Fa�{b�{c�{d�{e���P�V�Q
�m�P�n���Aa�{b�{c���V�W
�m�Q�n���Aa�{b�{d���W�P
�m�R�n���Ac�{d�{e���P�R�T
�m�S�n���Aa�{d�{e���P�P�S�A�܂��́Ab�{c�{e���P�P�S
�i��Ԗڂɏd���g�����́A���{���{���ł��邪�A�O�Ԗڂ͏�L�̓�ʂ肪�l������j
�i1�j�b�A�c�A�d�̏d��
�^���m�P�n�{�^���m�R�n���Aa�{b�{�Qc�{d�{e���Q�P�R�@�������A
a�{b�{c�{d�{e���P�V�Q�Ƃ̔�r����A�����S�P�ƂȂ�B
�@�@�������S�P
�^���m�Q�n�|�^���m�P�n���A���|�����R
�@�@���������{�R���S�S
�^���m�R�n���A�����P�R�T�|���|��
�@�@�������T�O
�i�Q�j�`�A�a�̏d��
a�{d�{e���P�P�S�̏ꍇ�F
�@�@a���P�P�S�|d�|e���Q�O
�@�^���m�P�n���Ab=�V�W-a�|c���P�V
�@�����ŁAa��b�Ȃ̂ŁA�^�������Ȃ��B
b�{c�{e���P�P�S�̏ꍇ�F
�@�@b=�P�P�S-c-e=�Q�R
�@�^���m�P�n���Aa=�V�W-b�|c���P�S
�@�����ŁAa��b�@�Ȃ̂ŁA�^�������B
�@�@��a=�P�S�Ab=�Q�R
�E����4
�i�y���l�|���F�I���W�j
��������@
[�O]�@�`�{�a�{�b�{�c�{�d���P�V�Q
[�P]�@�`�{�a�{�b���V�W
[�Q]�@�`�{�a�{�c���W�P
[�R]�@�b�{�c�{�d���P�R�T
[�S]�@�i�A�j�`�{�c�{�d���P�P�S�@�@�܂��́@�i�C�j�a�{�b�{�d���P�P�S
[�P]�{[�R]�|[�O]���@�b���S�P�@�@�@���ꂩ��[�P]���@�`�{�a���R�V�@��[�Q]���
�c���S�S�@�@[�R]�́@�S�P�{�S�S�{�d���P�R�T�@
�@�]���ā@�d���T�O
�@�����Łi�A�j���������Ƃ���Ɓ@�`�{�S�S�{�T�O���P�P�S�@�]���Ă`-���Q�O�C�a���P�V
�ƂȂ薵���@��@�`���a�@
�@�����Łi�C�j���������Ƃ���Ɓ@�a�{�S�P�{�T�O���P�P�S�@�]���Ăa-���Q�R�C�`���P�S
�ƂȂ�B
�@���@�i�P�j�b���S�Pg�@�C�c���S�Sg�@�C�d���T�Og �i�Q�j�`���P�Sg �C�a-���Q�Rg
�E����5
�i�y���l�|���F�܁[��������Ƃ��j
�i�P�j
�`�{�a�{�b�@�@�@�@�@���@�V�W�@�E�E�E�E�s1�t
�`�{�a�@�@ �{�c�@�@ ���@�W�P�@�E�E�E�E�s2�t
�@�@�@�@ �b�{�c�{�d���P�R�T�@�E�E�E�E�s3�t
�`�{�a�{�b�{�c�{�d���P�V�Q�@�E�E�E�E�s4�t
�s3�t�Ɓs4�t����
�@�`�{�a���R�V�@�@�@�@�@�@�@�@ �E�E�E�E�s5�t
�s1�t�Ɓs5�t����
�@�b���S�P
�s2�t�Ɓs5�t����
�@�c���S�S
�s3�t���
�@�d���T�O
���@�@�b���S�P���@�c���S�S���@�d���T�O��
�i�Q�j
�u�R�Ԗڂɏd���g�����̂Ƃ����ς̏d���͂R�Wg�v�Ȃ̂ŁA�s6�t���s7�t�̂ǂ��炩����������B
�@�`�@�@�@�@�@�@�c�{�d���P�P�S�@�E�E�E�E�s6�t
�@�@�@�a�{�b�@�@ �{�d���P�P�S�@�E�E�E�E�s7�t
�@�s6�t�̏ꍇ�@�`���Q�O�@�a���P�V�@�ƂȂ� �@�`���a�@�����Ȃ�
�@�s7�t�̏ꍇ�@�`���P�S�@�a���Q�R
���@�@�`���P�S���@�a���Q�R��
�E����6
�i�y���l�|���F�l�c�@�����j
�i�P�j
�`�`�d�̏d�������ꂼ�ꂁ�C���C���C���C���i���j�Ƃ���D[�R]�܂ł̏�������C
�@�@�O���������������������c�c�c�s1�t
�@�@���{���{���{���{�����R�S.�S�~�T���P�V�Q�c�c�c�s2�t
�@�@���{���{�����Q�U�~�R���V�W�c�c�c�s3�t
�@�@���{���{�����Q�V�~�R���W�P�c�c�c�s4�t
�@�@���{���{�����S�T�~�R���P�R�T�c�c�c�s5�t
�s2�t�|�s3�t����C
�@�@���{�����X�S�c�c�c�s6�t
�s5�t�|�s6�t����C
�@�@�����S�P�c�c�c�s7�t
�s2�t�|�s4�t����C
�@�@���{�����X�P�c�c�c�s8�t
�s8�t�|�s7�t����C
�@�@�����T�O�c�c�c�s9�t
�s9�t�|�s6�t����C
�@�@�����S�S�c�c�c�s10�t
�����́s1�t�����D
�̂ɂb�C�c�C�d�̏d���͂��ꂼ��S�P���C�S�S���C�T�O���ƂȂ�D
�i�Q�j
�s4�t�|�s10�t����C
�@�@���{�����R�V�c�c�c�s11�t
[�S]�̂R�Ԗڂɏd���g�������l����̂��ʓ|�Ȃ̂ŁCVBSCRIPT�ŋ��߂��D
'185.vbs
dim w(10)
c=41:d=44:e=50
k=1/4
for a=0 to 37/2 step k
b=37-a
w(1)=a+b+c
w(2)=a+b+d
w(3)=a+b+e
w(4)=a+c+d
w(5)=a+c+e
w(6)=a+d+e
w(7)=b+c+d
w(8)=b+c+e
w(9)=b+d+e
w(10)=c+d+e
for j=1 to 9
for jj=j+1 to 10
if w(j)>w(jj) then
w(0)=w(j)
w(j)=w(jj)
w(jj)=w(0)
end if
next
next
if w(8)=38*3 then
msgbox a&","&b&","&c&","&d&","&e
end if
next
���̃v���O�����ɂ��C�`�C�a�̏d���͂��ꂼ��P�S���C�Q�R���ƂȂ�D
�E����7
�i�y���l�|���F�}�V���j
�܂��A�ł��y���g�ƍł��d���g����
�@�@A+B+C=26*3
�@�@C+D+E=45*3
�Ƃ������Ƃ�������B
����ɍ��v�̕��ς�34.4�Ȃ̂ŁA
�@�@A+B+C+D+E=34.4*5
�ł���B�����̂��Ƃ���AC=41, A+B=37, D+E=94�Ƃ������Ƃ�������B
����2�ԖڂɌy���g���l����B���̑g�́AA, B, D�ł���B
�@�@A+B+D=27*3
A+B=37����D=44�ƕ�����B�����D+E=94�������̂ŁAE=50�ł���B�ȏォ��
�@�@(1) C 41g, D 44g, E 50g
���ɂR�Ԗڂɏd���g�ݍ��킹���l����B(2�Ԗڂɏd���g��E,D,B)
���Ƃ��čl������g�́A(E,D,A) or (E,C,B)��2�g�ł���B
(E,D,A)�̏ꍇ�AA=20, B=17�ƂȂ��Ă��܂��A��蕶�̏���(A��B)�ɓ��Ă͂܂�Ȃ�
(E,C,B)�̏ꍇ�AA=14, B=23�ƂȂ�B
�ȏォ��
�@�@(2) A 14g, B 23g
�y�ߒ��z
�܂��AA����E�܂ł̑g�ݍ��킹�ĉ��O�����ɂȂ邩�}�����Ă��ꂩ���������l���Ă����܂����B
����͓��ɂЂ�������ꍇ�����������ł͂Ȃ������̂ŁA����Ȃ蓚���ɂ��ǂ蒅���܂����B
�܂��A(1),(2)�ƕ����邱�Ƃ��q���g�ɂȂ����Ǝv���܂��B
�E����8
�i�y���l�|���F���Y���j
�s1�t�`�a�b�c�d���R�S�D�S�~�T���P�V�Q
�s2�t�`�a�b�@�@���Q�U�@�@�~�R���@�V�W
�s3�t�@�@�@�c�d���P�V�Q�|�V�W���@�X�S
�s4�t�`�a�@�c�@���Q�V�@�@�~�R���@�W�P
�s5�t�@�@�b�@�d���P�V�Q�|�W�P���@�X�P
�s6�t�@�@�b�c�d���S�T�@�@�~�R ���P�R�T
�s3�t�Ɓs6�t���@�b���S�P��
�s5�t���@�@�@ �d���T�O��
�s3�t���@�@�@ �c���S�S��
�܂�A
�`�a�{�S�P�{�S�S�{�T�O���P�V�Q
�`�{�a���R�V
�P�Ԗڂɏd���̂́A�b�c�d���P�R�T
�Q�Ԗڂɏd���̂́A�a�c�d
�R�Ԗڂɏd���̂�
�`�{�c�S�S�{�d�T�O���P�P�S�@�@���̏ꍇ�A�`���Q�O�@�@�a���P�V�@�@�s��
��
�a�{�b�S�P�{�c�S�S���P�P�S�@�@���̏ꍇ�@�a���Q�X�@���@�`���W�@�@�@�n�j
��
�a�{�b�S�P�{�d�T�O���P�P�S�@�@���̏ꍇ�A�a���Q�R�@���@�`���P�S�@�@�n�j
�`�a�b�c�d���@�W�^�Q�X�^�S�P�^�S�S�^�T�O�̎��́A
�P�Ԗڂɏd���̂��A�b�c�d���P�R�T
�Q�Ԗڂɏd���̂��A�a�c�d���P�Q�R
�R�Ԗڂɏd���̂��A�a�b�d���P�Q�O
�S�Ԗڂɏd���̂��A�a�b�c���P�P�S
�`�a�b�c�d���A�P�S�^�Q�R�^�S�P�^�S�S�^�T�O�̏ꍇ�́@
�P�Ԗڂɏd���̂��A�b�c�d���P�R�T
�Q�Ԗڂɏd���̂��A�a�c�d���P�P�V
�R�Ԗڂɏd���̂��A�a�b�d���P�P�S�@�ŏ����ɍ���
�܂�
�`���P�S���A�a���Q�R��
�E����9
�i�y���l�|���F������͑����j
�T�̑��ʂ́@34.4�~5=172�@����āAA+B+C+D+E=172
[1]�̏�������AA+B+C=26�~3=78�@����ā@D+E=172-78=94
[2]�̏�������AA+B+D=27�~3=81�@����ā@C+E=172-81=91
[3]�̏�������AC+D+E=45�~3=135�@����ā@C=135-94=41�AD=135-91=44
�@�@���������āAE=135-41-44=50
[4]�̏����̂R�Ԗڂɏd���ꍇ�́AA�AD�AE�܂��́AB�AC�AE�̑g�ݍ��킹�ł���B
�@�@�O�҂����肷��ƁA��������AA+D+E=38�~3=114�@����ā@A=114-44-50=20�AB=78-20-41=17
����́AA��B���d���Ȃ�A�s�K�B
�@�@��҂����肷��ƁA��������AB+C+E=38�~3=114�@����ā@B=114-41-50=23�AA=78-23-41=14
�i�P�j�̓����́A41, 44, 50
�i�Q�j�̓����́A14, 23
�E����10
�i�y���l�|���F�̂�����j
�@�@A+B+C+D+E=172
�ł��y���g�����́iA,B,C)������
�@�@A+B+C=78
2�ԖڂɌy���g�����́iA,B,D)������
�@�@A+B+D=81
�ł��d���g������(C,D,E)������
�@�@C+D+E=135
�ȏ��� C=41 D=44 E=50 A+B=37
3�Ԗڂɏd���g������(A,D,E)��(B,C,E)�̂����ꂩ�ł���
A+D+E=114 �Ƃ����A=20 B=17 �ƂȂ艼��ɔ�����
����� B+C+E=114 A=14 B=23
�E����11
�i�y���l�|���F���q�̗Y�L�j
�T�̂�������y���ق����珇�ɕ��ׂ�ƁA�`�C�a�C�b�C�c�C�d�ł��B
���̂T�̏d���̍��v��172g
�@[1]�@�ł��y���g�����`�C�a�C�b�̂Ƃ��A�d���̍��v��78g
�@[2]�@�Q�ԖڂɌy���g�����`�C�a�C�c�̂Ƃ��A�d���̍��v��81g
�@[3]�@�ł��d���g�����b�C�c�C�d�̂Ƃ��A�d���̍��v��135g
����āA���v�|[1]�@���c�C�d�̍��v��94g�@....�@[4]�@
�@[2]�|[1]���@�b�Ƃc�̍���3g�@....�@[5]�@
�@[3]�|[4]���@�b��41g�@....�@[6]�@
�@[3]��[5]��[6]���@�c��44g�@�d��50g�i135-44-41�j
�@���v�|[3]���@�`�Ƃa�̍��v��37g
���āA�@�R�Ԗڂɏd���g�����͉����H
���̂Ƃ��A�d���̍��v��114g�@�ł����B
�ł��d���g�������b�C�c�C�d
�Q�Ԗڂɏd���g�������a�C�c�C�d
���āA�R�Ԗڂɏd���g�����́A
�@�@[��]�@�a�C�c�C�d�̂a���`�ɕς����@�`�C�c�C�d
�@�@[��]�@�a�C�c�C�d�̂c���b�ɕς����@�a�C�b�C�d
�̂����ꂩ�̂͂��B���ꂼ��̏d������
�@�@[��]�@�`�{44�{50��114
�@�@[��]�@�a�{41�{50��114
�Ȃ̂ŁA
�@�@[��]�@�`��20�@�ƂȂ�@�a��17g
�@�@[��]�@�a��23�@�ƂȂ�@�`��14g
�������`���a�Ȃ̂�[��]�͕s�K�B
����Ă`�C�a�C�b�C�c�C�d�͏���14�A23�A41�A44�A50�ig�j
�E����12
�i�y���l�|���FTeki�j
(1) �b���S�P�C�c���S�S�C�d���T�O
(2) �`���P�S�C�a���Q�R
����@��
(1) �T�̕��ς��R�S�D�S���Ȃ̂ŁA�T�̏d���̍��v�͂P�V�Q���B
�����P�ƂR����A�`�{�a�{�b�{�b�{�c�{�d���V�W�{�P�R�T���Q�P�R���B
����āA�b���S�P���B
�����Q����A�`�{�a�{�c���W�P���A�܂��A�`�{�a���R�V���B
����āA�c���S�S���B
����Ə����R����A�d���P�R�T�|�S�S�|�S�P���T�O���B
(2) �����S�̏ꍇ���������܂��B
�T �R�Ԗڂɏd���̂��A�`�{�c�{�d�̂Ƃ��A
�@�@�`���R�W�~�R�|�S�S�|�T�O���Q�O��
�ł����A���̂Ƃ��A�a���P�V���ƂȂ�s�K�B
�U �R�Ԗڂɏd���̂��A�a�{�b�{�c�̂Ƃ��A
�@�@�a���R�W�~�R�|�S�P�|�S�S���Q�X���B
���̂Ƃ��A�`���W���ƂȂ�܂����A���ꂾ�ƁA�R�Ԗڂɏd���̂��a�{�b�{�c
�łȂ��A�a�{�b�{�d���P�Q�O���̎��ƂȂ�A�s�K�B
�V �R�Ԗڂɏd���̂��A�a�{�b�{�d�̂Ƃ��A
�@�@�a���R�W�~�R�|�S�P�|�T�O���Q�R���B
���̂Ƃ��A�`���P�S���B
����͑�ӂ����܂��B
�E����13
�i�y���l�|���F�܂߁j
�܂��͂��߂ɁA2�ԖڂɌy���g�ݍ��킹�A3�Ԗڂɏd���g�ݍ��킹�ɂ��čl�@����B
�ł��y���g�ݍ��킹���iA�CB�CC�j�ł��邱�Ƃ͎����B
2�ԖڂɌy���g�ݍ��킹�́A���̒��̂ǂꂩ���A���ɏd��D�ɒu�����������́B
���̍ہA���ʂ��ł��邾���������Ȃ�悤�ɂ������̂ŁA
A��B��C���AD-A��D-B��D-C�ł��邩��A���̒��ōł����ʂ����������̂�C��D�ɒu�����������́B
�]���āA2�ԖڂɌy���g�ݍ��킹�́iA�CB�CD�j�ł���B
����3�Ԗڂɏd���g�ݍ��킹�B
�y���g�ݍ��킹�Ɠ��l�ɍl���āA2�Ԗڂɏd���g�ݍ��킹�́iB�CD�CE�j�ł���B
3�Ԗڂɏd���g�ݍ��킹�́A���̒��̂ǂꂩ���AA�܂���C�ɒu�����������́B
���̍ہA���ʂ��ł��邾���������Ȃ�悤�ɂ������̂ŁA
B��A�ɁAD��C�ɒu�����������̂����ƂȂ�B
�]���āA3�Ԗڂɏd���g�ݍ��킹�́iA�CD�CE�j�܂��́iB�CC�CE�j�ł���B
�ȏ�̍l�@�ƍ��킹�A�^����ꂽ�����𐔎������Ă����B
�y������A�AB�AC�AD�AE�@���@A��B��C��D��E�@�s1�t
���ϒl��34.4�@���@A+B+C+D+E=34.4�~5��172�@�s2�t
�ł��y���g�ݍ��킹�̕��ϒl��26�@���@A+B+C=26�~3=78�@�s3�t
2�ԖڂɌy���g�ݍ��킹�̕��ϒl��27�@���@A+B+D=27�~3=81�@�s4�t
�ł��d���g�ݍ��킹�̕��ϒl��45�@���@C+D+E=45�~3=135�@�s5�t
3�Ԗڂɏd���g�ݍ��킹�̕��ϒl��38�@���@A+D+E=38�~3=114�@�s6�t�@�܂��́@B+C+E=114�@�s7�t
�s3�t�Ɓs5�t��ӁX������
�@�@A+B+2C+D+E=213�@�s8�t
�s2�t�Ɓs8�t��ӁX������
�@�@C=41�@�s9�t
�s3�t�Ɓs4�t��ӁX������
�@�@C-D=-3�@�s10�t
�s9�t�Ɓs10�t���
�@�@D=44�@�s11�t
�s5�t�Ɓs9�t�Ɓs11�t���
�@�@E=50�@�s12�t
�s6�t�A�s11�t�A�s12�t���
�@�@A=20�@�s13�t
�s3�t�Ɓs9�t�Ɓs13�t���
�@�@B=17�@�s14�t
�ł��邪�A�s13�t�Ɓs14�t�ł́s1�t���s�����B
����A�s7�t�Ɓs9�t�Ɓs12�t����́A
�@�@B=23�@�s15�t
�s3�t�Ɓs9�t�Ɓs15�t���
�@�@A=14�@�s16�t
�ƂȂ�A�s1�t�������B
�ȏ���iA�CB�CC�CD�CE�j���i14�C23�C41�C44�C50�j
�E����14
�i�y���l�|���FSOU�j
���m�肷�����
| 5�̕��� | a | +b | +c | +d | +e | = 34.4*5 | = 172 | �s1�t |
| ����[1] | a | +b | +c | = 26*3 | = 78 | �s2�t | ||
| ����[2] | a | +b | +d | = 27*3 | = 81 | �s3�t | ||
| ����[3] | c | +d | +e | = 45*3 | = 135 | �s4�t |
���m�肷�����
| ����[4-1] | b | +c | +e | = 38*3 | = 114 | �s5�t | ||
| ����[4-2] | a | +d | +e | = 38*3 | = 114 | �s6�t |
��������������������
�s5�t�𗘗p��(a,b,c,d,e)=(14,23,41,44,50)�s7�t
�s6�t�𗘗p��(a,b,c,d,e)=(20,17,41,44,50)�s8�t
�s8�t��a��b�̑召���t�ɂȂ�̂ŁA
�s7�t�݂̂������B
�E����15
�i�y���l�|���F�X���[�N�}���j
(1) A+B+C =78
(2) A+B +D =81
(3) C+D+E=135
(4) A +D+E=114...3�ԖڂɎv���P�[�X�͂��� or B+C+E
(5) B+C +E=108
(6) A+B+C+D+E=172
C=(1)+(3)-(6)=78+135-172=41
D=(2)+(3)-(6)=81+135-172=44
E=(4)+(5)-(6)=114+108-172=50
A=(1)+(4)-(6)=78+114-172=30
B=(2)+(5)-(6)=81+108-172=17
���̉��ƁA
A��B�̏����ɍ���Ȃ��̂ŁA�s�K...
�����...
(4) B+C +E=114
(5) A +D+E=108
�Ƃ���Ȃ�..
A=78+108-172=14
B=81+114-172=23
�Ɩ��������Ă킯�ł��� ^^
�E����16
�i�y���l�|���FT_Tatekawa�j
A + B + C + D + E = 172
[1] A + B + C = 26 x 3 = 78
[2] A + B + D = 27 x 3 = 81
[3] C + D + E = 45 x 3 = 135
(1)
[1][3] ���
A + B + 2 x C + D + E = 78 + 135 = 213
�����
C = 213 - 172 = 41
[1][2] ���
D - C = 3
������
D = 41 + 3 = 44
[3] ���
E = 135 - 41 - 44 = 50
(2)
2�Ԗڂɏd���g�ݍ��킹��
B + D + E
�ł���D���̂������1��u�����������̂�3�Ԗڂɏd���g�ݍ��킹�ł���D
3�Ԗڂɏd���g�ݍ��킹 [4] ��
A + D + E
B + C + E
�̉\��������D
(i) A + D + E �̏ꍇ
�@A + D + E = 38 x 3 = 114
�@�Ȃ̂�
�@A = 114 - 50 - 44 = 20
�@[1] ���
�@B = 78 - 41 - 20 = 17
�@�ƂȂ� A �� B �Ȃ̂ŕs�K�D
(ii) B + C + E �̏ꍇ
�@B + C + E = 114
�@�Ȃ̂�
�@B = 114 - 50 - 41 = 23
�@[1] ���
�@A = 78 - 41 - 23 = 14
�@�ƂȂ�D
�@A + D + E = 108�CB + C + D = 108 ������ B + C + E �͂������d���̂ŁA���������D
�����(ii)�̂ݏ��������CA = 14, B = 23 �ł���D
�E����17
�i�y���l�|���F��ӂ����̂炢��������j
���T�̂����肩��R��g�ݍ��킹��ꍇ�̐��͎��̂P�O�ʂ�ł��B
�@�@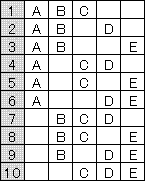
�������y�����ɐ������Ă݂܂��B
�E��Ԍy���̂́A
�@�@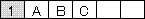
�E���Ɍy���̂́A
�@�@
�E���̃��x���́A
�@B���d���Ȃ�ꍇ��D���d���Ȃ�ꍇ�Ȃ̂ŁA�4����3��̏ꍇ�ł��B
�i���̂ǂ��炪�d�����͕�����܂���j
�@�@
�E�����x���́A�4���A��D���d���Ȃ�ꍇ�A���邢�͢3���B���d���Ȃ�ꍇ�ł��B
�4���D���d���Ȃ�ꍇ�Ƣ3���B���d���Ȃ�ꍇ�͓������ʂɂȂ�܂��B
(�7��Ƣ5��̂ǂ��炪�d�����͕�����܂���)
�@�@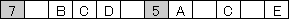
�E�����x���́A�7���D���d���Ȃ�ꍇ�A���邢�͢5���A��C���d���Ȃ�ꍇ�ł��B
�7���D���d���Ȃ�ꍇ�Ƣ5���A���d���Ȃ�ꍇ�͓������ʂɂȂ�܂��B
(�8��Ƣ6��̂ǂ��炪�d�����͕�����܂���)
�@�@
�E���́A�8���C���d���Ȃ�ꍇ���6���A���d���Ȃ�ꍇ�ł��B���̂Q�͓������ʂɂȂ�܂��B
�@�@
�E��ԏd���̂́A
�@�@
�i�P�j�ȏォ������������Ă܂��B
�@�@[0]���̂T�̕��ς̏d���́A�R�S�D�Sg�@�ł����B
�@�@[1]�@�ł��y���g�����̂Ƃ��A���ς̏d���͂Q�Ug�@�ł����B
�@�@[2]�@�Q�ԖڂɌy���g�����̂Ƃ��A���ς̏d���́A�Q�Vg�@�ł����B
�@�@[3]�@�ł��d���g�����̂Ƃ��A���ς̏d���͂S�Tg�@�ł����B
���A
�@�@A �{�@B �{�@C �{�@D �{�@E ���@34.4�~5��172����s1�t
�@�@A �{�@B �{�@C �@ ���@26�~3��78����s2�t
�@�@A �{�@B�@�{D��27�~3��81����s3�t
�@�@C �{ D �{ E �� 45�~3��135����s4�t
�s1�t�|�s4�t���A
�@�@A �{ B ��37����s5�t
�s2�t�|�s5�t�A�s3�t�|�s5�t���A
�@�@C �� 41 ����s6�t
�@�@D �� 44 ����s7�t
�s1�t�|�s5�t�|�s6�t�|�s7�t���A
�@�@E��50
�i�Q�j���ɁA
�@�@[4]�@�R�Ԗڂɏd���g�����̂Ƃ��A���ς̏d���͂R�Wg�@�ł����B
�ɊY������̂́A�8����6��̏ꍇ�ł��B
�E�8��̂Ƃ��A
�@�@B �{ C �{ E �� 38�~3��114
�@�@A �{ B �� 37
���
�@�@B��114�|41�|50��23
�@�@A��37�|23��14
�E�6��̂Ƃ��A
�@�@A�{D�{E��38�~3��114
�@�@A�{B��37
�@���
�@�@A��114�|44�|50��23
�@�@B��37�|23��14
�ƂȂ�܂����AA��B�ł͂Ȃ��̂ŁA�Y�����܂���B
�E����18
�i�y���l�|���F�O�p��K�j
(1)
5 �̂�����̏d���� A�CB�CC�CD�CE (A��B��C��D��E) �Ƃ���ƁC
5 �̏d���̕��ς��� A�{B�{C�{D�{E��172�@�c�s1�t
����[1]���@�@�@�@�@�@�@A�{B�{C��78�@�c�s2�t
����[3]���@�@�@�@�@�@�@C�{D�{E��135�@�c�s3�t
�s2�t�{�s3�t�|�s1�t ���@C��41 g�@�c�s4�t
�s2�t�s4�t���@�@�@�@�@�@�@A�{B��37�@�c�s5�t
�s3�t�s4�t���@�@�@�@�@�@�@D�{E��94�@�c�s6�t
����[2]���@�@�@�@�@�@�@A�{B�{D��81�@�c�s7�t
�s5�t�s6�t�s7�t���@�@�@�@�@D��44 g�CE��50 g�@�c�s8�t
(2)
3 �Ԗڂɏd��������̑g�ݍ��킹�́C(B�CC�CE) �� (A�CD�CE) ���l�����C
(i) B�{C��A�{D �̂Ƃ� 3 �Ԗڂ� (A�CD�CE) �ŁC����[4]��� A�{D�{E��114�@�c�s9�t
�s5�t�s6�t�s7�t��� A��20�CB��17 �ƂȂ邪�C����� A��B �������s�K�B
(ii) A�{D��B�{C �̂Ƃ� 3 �Ԗڂ� (B�CC�CE) �ŁC����[4]��� B�{C�{E��114�@�c�s10�t
�s4�t�s5�t�s8�t�s10�t��� B��23 g�CA��14 g �ŁC����͑�ӂ����B
�E����19
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
�����@�`���P�S�@�a���Q�R�@�b���S�P�@�c���S4�@�d���T�O�@�ł��B
�`�D�a�D�b�D�c�D�d
����
�s1�t�@�`�{�a�{�b�{�c�{�d���R�S�D�S�~�T���P�V�Q
�s2�t�@�`�{�a�{�b���Q�U�~�R���V�W
�s3�t�@�b�{�c�{�d���S�T�~�R���P�R�T
�@�@�`�{�a���P�V�Q�|�P�R�T���R�V
�s4�t�@�`�{�a�{�c���Q�V�~�R���W�P
�O�Ԗڂɏd���g�����͎��̒ʂ�ł��B
�s5�t�@�`�{�c�{�d���R�W�~�R���P�P�S
���́s6�t�@�a�{�b�{�d���R�W�~�R���P�P�S
�s7�t�@�a�{�b���P�V�Q�|�P�P�S���T�W
���́s8�t�`�{�c���P�V�Q�|�P�P�S���T�W
��L�������ɂ`�A�a�A�b�A�c�A�d�����߂܂��B
�@�b���s2�t�{�s3�t�\�s1�t���i�`�{�a�{�b�j�{�i�b�{�c�{�d�j�|�i�`�{�a�{�b�{�c�{�d�j��
�V�W�{�P�R�T�|�P�V�Q���S�P�E�E�E�E�s9�t
�@�c���s3�t�{�s4�t�|�s1�t���i�b�{�c�{�d�j�{�i�`�{�a�{�c�j�\�i�`�{�a�{�b�{�c�{�d�j��
�P�R�T�{�W�P�|�P�V�Q���S�S�E�E�E�E�s10�t
�s9�t�Ɓs10�t���s3�t�ɑ������
�@�d���P�R�T�|�S�P�|�S�S���T�O�E�E�E�E�s11�t
�s7�t�ɂb���S�P��������
�@�a���T�W�|�S�P���P�V
�s8�t�ɂc���S�S��������
�@�`���T�W�|�S�S���P�S
�a���P�V�Ƃ���Ƃ`���R�V�|�P�V���Q�O
���ꂾ�Ƃ`���a�ɖ�������̂�
�`���P�S�Ƃ��Ăa���R�V�|�P�S���Q�R�ƂȂ�
����ł��ׂĂ̏����ɍ��������ƂɂȂ�܂��B
�E����20
�i�y���l�|���F�q����1128�j
�R�̂������I�Ƃ����̑g�ݍ��킹���T�b�R=10�ʂ�ƂȂ�܂��B
��ӂ�������A����������Ɓi�P�ʂ͂��j���̂悤�ɂȂ�܂�
�`���a���b���c���d�@�@�@�@�@�@�@�@�E�E�E�s1�t
�`+�a+�b+�c+�d��34.4�~5��172�@�@ �E�E�E�s2�t
�R�̂�����̑g�ݍ��킹�̊W���@�ɏ]���ĕ\���Ǝ��̂悤�ɂȂ�܂�
�@�@�`+�a+�b���`+�a+�c���`+�a+�d
�@�@�`+�b+�c���`+�b+�d���`+�c+�d
�@�@�a+�b+�c���a+�b+�d���a+�c+�d���b+�c+�d
�@�@�`+�a+�b��26�~3��78�@�@�@�@�@�@�@�E�E�E�s3�t�@[1](�s1�t���玩��)
�@�@�`+�a+�c��27�~3��81�@�@�@�@�@�@�@�E�E�E�s4�t�@[2](�s1�t���玩��)
�@�@�b+�c+�d��45�~3��135�@�@�@�@�@�@ �E�E�E�s5�t�@[3](�s1�t���玩��)
�����łR�Ԗڂɏd���g�ݍ��킹�͂`+�c+�d�Ƃa+�b+�d�̂ǂ��炩�ɂȂ�܂���
�@�@�`+�c+�d��38�~3��114���^�Ȃ�
�@�@�a+�b+�d��38�~3��114�@���U
�ȏ�܂���
�s2�t�s3�t�s5�t����b���S�P
�s3�t����`�{�a��78-41��37
�s4�t����c��81-37��44
�s5�t����d��135-44-41��50
�`+�c+�d��114�Ȃ�`��20�A�a��17
�s1�t ����U
�����
�a+�b+�d��114�Ȃ�a��23�A�`��14
���^
�@�@�`���P�S
�@�@�a���Q�R
�@�@�b���S�P
�@�@�c���S�S
�@�@�d���T�O
�R�����g
�^����ꂽ���������Ă����K�v������܂��B���ɁA
�@�@���� [4]�@�R�Ԗڂɏd���g�����̂Ƃ��A���ς̏d���͂R�Wg�@�ł����B
�ɂ��ẮA�ꍇ�������K�v�ɂȂ�܂��B
 top
top