問題184　５枚のカード

２，３，４，５，６の数が書かれたカードが１枚ずつ、合計５枚ある。これらのカードを無作為に横１列に並べたとき、どのｉ＝１，２，３，４，５に対しても左からｉ番目のカードに書かれた数がｉ以上となる確率を求めてください。

問題の出典

数学オリンピック
日本評論社
第18回日本数学オリンピック予選(2008年)

解答

～到着順にご紹介します～

解答・その1

（ペンネ－ム：haya）

答： 13.333…%

【解き方】
許されるカードの組合せは下の16通り、
　　23456
　　23465
　　23546
　　23645
　　24356
　　24365
　　25346
　　26345
　　32456
　　32465
　　32546
　　32645
　　42356
　　42365
　　52346
　　62345
従って確率は、
　　16/5! = 16/120 = 13.333・・・
となる。

解答・その2

（ペンネ－ム：迷子の雄猫）

解答184　５枚のカード
２，３，４，５，６の数が書かれたカードを以下「２」「３」「４」「５」「６」と記述する。
どのｉ＝１，２，３，４，５に対しても左からｉ番目のカードに書かれた数がｉ以上となるのだから、まず、場所が5箇所。
「２」は1番目か2番目。確率は2÷5。
残りの場所が4箇所。「３」は1番目から3番目。そのうち1箇所に「２」が置かれているので確率は(3-1)÷4。
残りの場所が3箇所。「４」は1番目から4番目。そのうち2箇所に「２」「３」が置かれているので確率は(4-2)÷3。
「５」「６」はどこに置いても条件を満たすから、求める確率は
　　(2÷5)×((3-1)÷4)×((4-2)÷3)=(2÷5÷3)=2/15

解答・その3

（ペンネ－ム：スモークマン）

全体の順序の数の和と実際の数の並びの和の差=5は常に保たれているので...
5=1+1+1+1+1...1
　=2+1+1+1...4!/3!=4
　=2+2+1...3!/2!=3
　=2+3...2!　　　　　　←たとえば...20300=32645, 30020=42365 に対応してる...
　=3+1+1...3!/2!=3
　=4+1...2!　　　　　　←40001=52346, 14000=26345
　=5...1

けっきょく...
1+4+3+2+3+2+1=16
16=2⁴ だから...一般に...2^n-1 になるんだろうか？
6=1+1+1+1+1+1...1
　=2+1+1+1+1...5!/4!=5
　=2+2+1+1...4!/2!2!=6
　=2+2+2...1
　=3+1+1+1...4!/3!=4
　=3+2+1...3!
　=3+3...1
　=4+1+1...3!/2!
　=4+2...2!
　=5+1...2!
　=6...1
合計=1+5+6+1+4+6+1+3+2+2+1=32=2⁵ になってる!!
なぜなのかはわからない...^^;...?
オイラーさんの整数分割ってのがあったはず...調べてみようかなぁ...??

確率は、
16/5!=16/120=2/15

解答・その4

（ペンネ－ム：浜田　明巳）

エクセルのマクロで解きました．答は２／１５です．データの掃き出しもするようにしています．

Option Explicit
Dim a(5) As Integer
Sub Macro1()
    Cells(1, 1).Value = 0
    Cells(1, 2).Value = 0
    Dim g As Integer
    Call saiki(1)
    g = GCD(Cells(1, 1).Value, Cells(1, 2).Value)
    Cells(1, 1).Value = Cells(1, 1).Value / g
    Cells(1, 2).Value = Cells(1, 2).Value / g
    Range("A1").Select
End Sub
Sub saiki(ByVal n As Integer)
    Dim dame As Integer
    Dim j As Integer
    a(n) = 2
    While a(n) <= 6
      If onaji(n) = 0 Then
        If n < 5 - 1 Then
          Call saiki(n + 1)
        Else
          a(5) = 6
          For j = 1 To 5 - 1
            a(5) = a(5) + (j + 1) - a(j)
          Next j
          dame = 0
          j = 1
          While dame = 0 And j <= 5
            If a(j) >= j Then
              j = j + 1
            Else
              dame = 1
            End If
          Wend
          Cells(1, 2).Value = Cells(1, 2).Value + 1
          If dame = 0 Then
            Cells(1, 1).Value = Cells(1, 1).Value + 1
            For j = 1 To 5
              Cells(Cells(1, 1).Value, j + 2).Value = a(j)
            Next j
            Range("C" & Cells(1, 1).Value).Select
          Else
            For j = 1 To 5
              If a(j) < j Then
                Cells(Cells(1, 2).Value - Cells(1, 1).Value, j + 7).Value = Str(a(j)) + "xxx"
              Else
                Cells(Cells(1, 2).Value - Cells(1, 1).Value, j + 7).Value = a(j)
              End If
            Next j
          End If
        End If
      End If
      a(n) = a(n) + 1
    Wend
End Sub
Private Function onaji(ByVal n As Integer) As Integer
    Dim j As Integer
    onaji = 0
    j = 1
    While onaji = 0 And j < n
      If a(j) = a(n) Then
        onaji = 1
      Else
        j = j + 1
      End If
    Wend
End Function
Private Function GCD(ByVal x As Integer, ByVal y As Integer) As Integer
    If y = 0 Then
      GCD = x
    Else
      GCD = GCD(y, x Mod y)
    End If
End Function

解答・その5

（ペンネ－ム：次郎長）

5枚を並べたとき、
（ｉ=5のとき）一番右端は、5もしくは6ならＯＫ。 (2,3,4,5,6)の5枚のうち2枚がＯＫ・・・・・・・・・・・・・2/5
（ｉ=4のとき）右から2番目は、4,5,6のどれか。
右端の1枚（5か6）が取られているので残り(2,3,4,5)もしくは(2,3,4,6)の4枚のうち
(4,5)もしくは（5,6）の2枚がOK・・・・・・・・・・・・・・2/4
（ｉ=3のとき）右から3番目は、3,4,5,6のどれか。ｉ=4とｉ=5で2枚とられるので
同様に考えて残り3枚のうち2枚がＯＫ・・・・・・・・・・・2/3
（ｉ=2のとき）左から2番目は、カードが2-6のどれでもＯＫ
（ｉ=1のとき）一番左は、カードがどれでもＯＫ
つまり2/5*2/4*2/3=2/15

解答・その6

（ペンネ－ム：転位反応）

i=1,2,3,4,5に対して、以下のような箱を設定して、題意を満たすようにカードを入れることを考える。

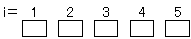
まず、２のカードは、i=1,または2の箱に入れることができて、２通りの方法がある。
次に、３のカードは、i=1,2,または3の箱に入れられるが、i=1,または2の箱には既に２のカードが入っているので、３のカードを入れることができる箱の組み合わせは２通りである。
さらに、４のカードは、i=1,2,3,4の箱に入れられるが、i=1,2,3のうち、２つの箱には既に２,３のカードが入っているので、４のカードを入れることができる箱の組み合わせも２通りである。
同様に、５のカード、６のカードを入れることができる箱の組み合わせは２通りである。
∴題意を満たすカードの並べ方は、２^４＝１６通り
一方、すべてのカードの並べ方は、５×４×３×２×１＝１２０通りなので
∴求める確率は、１６／１２０＝２／１５

解答・その7

（ペンネ－ム：のっこん）

横一列に並べた時、一番左の位置をA、右へ順にB、C、D、Eとする
　　 ABCDE
2が位置することができるのはAとB
3が　　　　　　　〃　　　　　　　 AとBとC
4が　　　　　　　〃　　　　　　　 AとBとCとD
5と6はどこにでも位置することができる

[1]2がA、3がB、4がCの時　　　（5がD、6がE）または（その逆）の2通り
[2]　〃　　　〃　 4がDの時　　　（5がC、6がE）または（その逆）の2通り
[3]　〃　 3がC、4がBの時　　　　同様に2通り
[4]　〃　　〃　　 4がDの時　　　　　　　〃
[5]2がB、3がA、4がCの時　　　（5がD、6がE）または（その逆）の2通り
[6]　〃　　　〃　 4がDの時　　　（5がC、6がE）または（その逆）の2通り
[7]　〃　 3がC、4がAの時　　　　同様に2通り
[8]　〃　　〃　　4がDの時　　　　　　　　〃

よって求める確率＝2・8/5！＝2/15
合計4枚の時は2、3、4、5のうち4と5がフリーになるから、確率は2・4/4！
合計3枚の時は2、3、4のうち3と4がフリーになるから、確率は2・2/3！
　　・・・・・・・・・・・・・・・・・・・
合計n枚の時の確率は、　2^n-1/n！　になると思います

（別解）似たようなもんですが・・・
x-y座標上の次の19個の格子点をマークする
（1、2）（2、2）
（1、3）（2、3）（3、3）
（1、4）（2、4）（3、4）（4、4）
（1、5）（2、5）（3、5）（4、5）（5、5）
（1、6）（2、6）（3、6）（4、6）（5、6）

このグラフ（？）を
2が左から1番目と2番目にしか存在しないこと
3が左から1番目と2番目と3番目にしか存在しないこと
4が左から1番目と2番目と3番目と4番目にしか存在しないこと
5と6は1番目から5番目のどこにでも存在しうることを示すものと考える
2について（1,2）を選んだ時
　3については（2、3）か（3、3）を選んで線で結ぶことになり・・・　
　結局　2・2・2・1＝8通り
2について（2、2）を選んだ時
　3については（1、3）か（3、3）を選んで線で結ぶことになり・・・
　結局　2・2・2・1＝8通り
あわせて16通り

解答・その8

（ペンネ－ム：アーベルト）

次の操作に影響しないよう大きい方から選んでいく
p5は2/5
p4は4枚になっているから2/4
p3は3枚になっているから2/3
p2=p1=1
よって2/5*2/4*2/3*1*1=2/15

解答・その9

（ペンネ－ム：kazz）

確率 = 条件を満たす場合の数 / 全ての場合の数を用いて求める。
5枚のカードの並べ方は全部で　5! = 120通り。
条件『どのi=1,2,3,4,5に対しても左からi番目のカードに書かれた数がi以上となる』については、右から条件を満たすような数字の並べ方を考えればよい。

一番右(i=5)・・・条件(5以上)を満たすカードは5,6の2枚。
よって一番右の並べ方は2通り。
右から2番目(i=4)・・・条件(4以上)を満たすカードは4,5,6の3枚。
うち1枚は先に並べてしまうので、それまでの並べ方それぞれに対して2通り。
右から3番目(i=3)・・・条件(3以上)を満たすカードは3,4,5,6の4通り。
うち2枚は先に並べてしまうので、それまでの並べ方それぞれに対して2通り。
同様にして右から4番目(i=2)も2通り。
一番左(i=1)は4枚目と同時に決まり、当然1以上なので1通り。
したがって条件を満たすカードの並べ方は　2×2×2×2×1=16通り。
よって確率は　16/120 = 2/15　(約13.3%)

樹形図にするとこんな感じ。

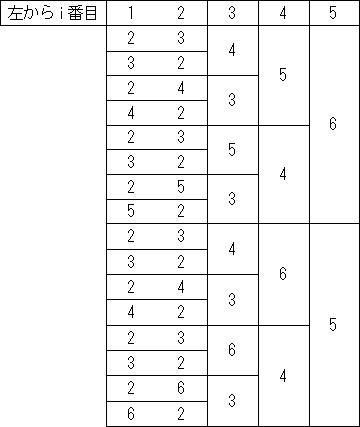
面白そうだったので、少し一般化してみる。
k枚のカード(2,3,・・・,k+1)を並べるとき、条件を満たすように並べられる確率は　2^k-1 / k !　。
→では、k枚のカード(3,4,・・・,k+2)だったら？
一番右がk,k+1,k+2の3通りなので、　3^k-1 / k !　かと思ったが、ずっと3通りではなく
枚数が減ると最後のほうは　・・・、3通り、2通り、1通りとなる。よって　(3^k-2×2 !) / k !　(k≧2)。
→そして、k枚のカード(1+j,・・・,k+j)を考えると、確率は　( (j+1) ^k-j× j ! ) / k !　(k-j≧0)。
k-j＜0、つまり最小の数(j+1)が枚数(k)を越えたらどんな並べ方でも条件を満たすので確率は1。

Excelで計算してみた。(濃い色から確率100%→10%以上→1%以上→1%未満)

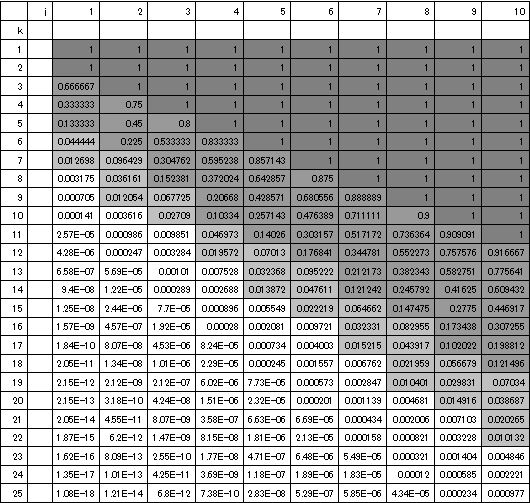
解答・その10

（ペンネ－ム：ちょろんは太太）

５番目のカードは、５または６。２通り
４番目のカードは、４、５、６のうち、５番目のカードで使われたものを除くので、２通り
３番目のカードは、３、４、５、６のうち、４番目のカードまでに使われた２枚を除くので、２通り。
２番目のカードは、２，３、４、５、６のうち、３番目のカードまでに使われた３枚を除くので、２通り。
１番目のカードは、５番目から２番目のカードで使われなかった残りの１枚。１通り
よって条件を満たす場合は、2×2×2×2×1=16
５枚のカードを無作為に並べた場合の総数は、1×2×3×4×5=120

よって、求める確率は、2/15

解答・その11

（ペンネ－ム：T_Tatekawa）

1) 1番目が6
条件を満たす並びは (6, 2, 3, 4, 5) しかない．
2) 1番目が5
条件を満たす並びは (5, 2, 3, 4, 6) しかない．
3) 1番目が4
最初の3つの並びが (4, 2, 3) でなければ条件を満たさない．
この場合，全体の並びとして 2 通りが条件を満たす．
4) 1番目が3
最初の2つの並びは (3, 2) でなければならない．
また，最後は 5 か 6 でなければならない．
3番目の数字と4番目の数字の入れ替わり，5番目の数字の選択の通りを考えると，全体の並びとして 2*2=4 通りが条件を満たす．
5) 1番目が2
2番目の数字が5か6だとすると，3番目以降は1), 2)と同じ．
2番目の数字が4だとすると，
最初の3つの並びが (2, 4, 3) でなければ条件を満たさない．
これは 3) の場合と同様で，全体の並びとして 2 通りが条件を満たす．
2番目の数字が3だとすると，4) と同様の考え方で4通りが条件を満たす．
条件を満たす並べ方は
　　1+1+2+4 + (1+1+2+4) = 16 通り
一方で，5枚のカードを横1列に並べる並べ方は
　　5! = 120通り
よって，条件を満たす確率は
　　16/120=2/15

解答・その12

（ペンネ－ム：まめ）

まず、５桁の数字をアトランダムに並べる並べ方は、
　　５！＝１２０通り。
次に、左からi番目の数字がi以上である確率を考える。
制約は右の桁ほど厳しくなるので、右から考えていく。

i＝５で題意を満たすのは、５か６のみ。
従って１２０×２÷５＝４８通りある。

この中からi＝４でも題意を満たすのは、４か、i＝５で残った方のみ。
従って４８×２÷４＝２４通り。

さらにi＝３でも題意を満たすのは、３か、i＝５、４で残った数字のみ。
従って２４×２÷３＝１６通り。

i＝２、１は制約がない。
以上より、１６÷１２０＝２／１５

今回の出題意図の考察ですが、場合分けは、制約条件が多いところから絞り込む、というポイントでしょうか。この問題を左の桁から解くと、場合分けが複雑になります。
実際にやってみます。
i＝１と２はどんな数字でもOKなので、i＝３から考えて、
　　３－４－５
　　３－４－６
　　３－５－６
　　３－６－５
　　４－５－６
　　４－６－５
　　５－４－６
　　６－４－５
以上の８通りそれぞれにi＝１、２の２！＝２通りがあるので、
８×２＝１６通り。
一応求められますが、抜け漏れがありそうで不安です。

解答・その13

（ペンネ－ム：浦岡）

左から
１番目には、２ｏｒ３ｏｒ４ｏｒ５ｏｒ６のカード
２番目には、２ｏｒ３ｏｒ４ｏｒ５ｏｒ６のカード
３番目には、３ｏｒ４ｏｒ５ｏｒ６のカード
４番目には、４ｏｒ５ｏｒ６のカード
５番目には、５ｏｒ６のカード
が並ぶことになる。このとき、右側から順に確率を考えていくと場合分けは不要である。
∴（求める確率）　=　２/５　×　２/４　×　２/３　×　２/２　×　１/１　=　２/１５　…（答）

解答・その14

（ペンネ－ム：まーりんａｎｄさとりん）

次の条件を同時に満足する並べ方を考えばよい。
　左から５番目：５か６
　左から４番目：４か５か６
　左から３番目：３か４か５か６
　左から２番目：２か３か４か５か６（左から３，４，５番目が決まれば残りなんでもよい）
　左から１番目：２か３か４か５か６（同上）

　４－２＼
  ２－４－３
　２－３＼  ＼
　３－２－４－５－６　　　　
　２－３－５－４／
　３－２／　／　
　２－５－３　
　５－２／

　４－２＼
　２－４－３
　２－３＼　＼
　３－２－４－６－５　　　　
　２－３－６－４／
　３－２／　／　
　２－６－３　
　６－２／

以上、１６通りが条件を満たす。
よって確率は１６／５！＝２／１５

解答・その15

（ペンネ－ム：Ryu1128）

先ず、カードを無作為に横一列に並べたときの場合の数は
　　₅Ｐ₅＝5！・・・[1]
次にどのｉ＝１，２，３，４，５に対しても左からｉ番目のカードに書かれた数がｉ以上となる場合を考えてみます。
右端に注目するとｉ=5でありここに入るのは5か6の2枚です。
次にｉ＝4では4,5,6
しかし5か6のいずれかが使われているので選択肢は2
同様に
ｉ＝3・・・3,4,5,6
4,5,6のうち2個が使われているので選択肢は2
ｉ＝2・・・2,3,4,5,6
3,4,5,6のうち3個が使われているので選択肢は2
ｉ＝1・・・2,3,4,5,6
2,3,4,5,6のうち4個が使われているので選択肢は1
よってｉ番目のカードに書かれた数がｉ以上となる場合の数は
　　2⁴・・・・[2]
よってｉ以上となる確率は[2]/[1]で
　　2⁴/5！＝2/15・・・・回答

解答・その16

（ペンネ－ム：夜ふかしのつらいおじさん）

カードが n 枚あるとき、条件を満たす場合の数をf（n）とします。
f（１）＝１は明らかです。

f（２）＝２です。

１番目に｛２｝をおくと、２番目に｛３｝をおくことになります。
何番目を表す数とおく数からそれぞれ１を引いて考えると１番目に｛２｝をおくことと同じになります。
このときの場合の数はf（１）と同じです。
１番目に｛３｝をおくと、２番目に｛２｝をおくしかありません。
つまりf（２）＝f（１）＋１です。

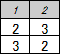
f（３）について考えます。

１番目に｛２｝をおくと、２・３番目に｛３，４｝をおくことになります。
何番目かを表す数とおく数からそれぞれ１を引いて考えると１・２番目に｛２，３｝をおくことと同じになります。
このときの場合の数はf（２）と同じです。
１番目に｛３｝をおくと、２番目には｛２｝をおくしかありません。
残り３番目に｛４｝をおくことになります。
何番目かを表す数とおく数からそれぞれ２を引いて考えると１番目に｛２｝をおくことと同じになります。
このときの場合の数はf（１）と同じです。
１番目に｛４｝をおくと、２・３番目に｛２，３｝をおくしかありません。

つまりf（３）＝f（２）＋f（１）＋１です。

このように考えると次のようになります。
　　f（n）＝f（n－１）＋f（n－２）＋f（n－３）＋・・・＋f（１）＋１

さて、f（１）＝１、f（２）＝２、f（３）＝４、f（４）＝８、f（５）＝１６、・・・です。
つまりf（n）＝２^n-1 です。

よって２，３，・・・，n＋１の数が書かれたカードを無作為に横１列に並べたとき、どのｉ＝１，２，・・・，nに対しても左からｉ番目のカードに書かれた数がｉ以上となる確率p（n）は、

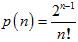
n＝５のときは、p（５）＝２⁴／５!＝２／１５（＝０．１３３・・・）です。

解答・その17

（ペンネ－ム：杖のおじさん）

答え　　確率は２/１５です
右端のカードから考えます。
[1]右端の５番目で条件に合う数字は５か６です。その確率は５分の２となります
[2]右橋から２番目で条件に合う数字は４と５と６（ただし、右側で使った数字１つを除く。その確率は４分の２となります。
[3]右橋から３番目で条件に合う数字は３と４か５か６（ただし、右側で使った数字２つを除く。その確率は３分の２となります。
右端から４番目と５番目はどの数字でも条件に合います。
上記により確率を求めます。
従って、この問題の確率は次の通りとなります。
答え　　2/5×2/4×2/3=2/15　です。

解答・その18

（ペンネ－ム：オヤジ）

５枚のカードを、横１列に並べる総数は、　５！＝１２０（通り）です。
条件を満たす並びは、
　６２３４５，５２３４６，４２３５６，４２３６５，３２４５６，３２４６５，
　３２５４６，３２６４５，２３４５６，２３４６５，２３５４６，２３６４５，
　２４３５６，２４３６５，２５３４６，２６３４５　の１６（通り）
従って　求める確率は、　１６／１２０＝　２／１５
　　　　　　　∴　２／１５

解答・その19

（ペンネ－ム：三角定規）

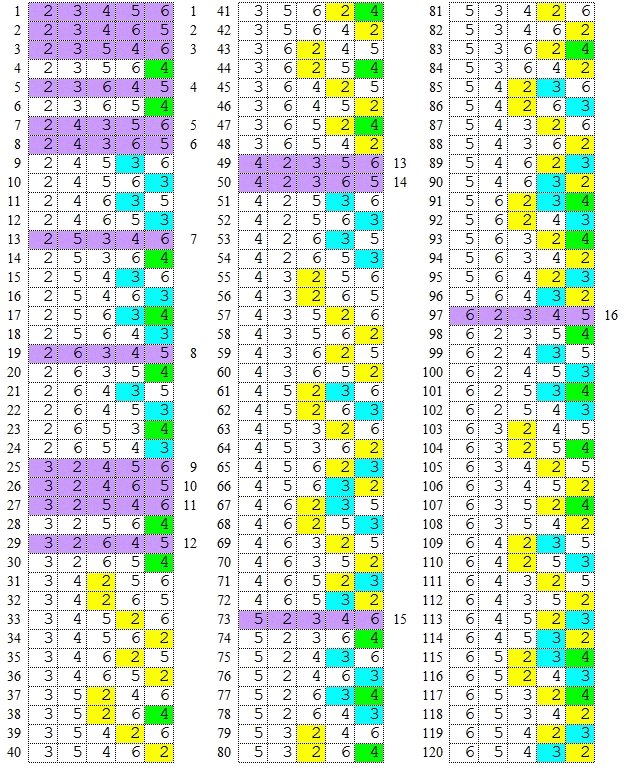
5個の数 2,3,4,5,6 を並べ替えてできる 5!＝120 個の順列は図の通りで，そのうち題意を満たすものは，藤色に着色した16個。
よって求める確率は，16/120＝2/15 (＝0.13…)　…[答]

確率は、起こり得るすべての場合の数と、条件を満たす場合の数を求めて、その比を考えます。
一般的に、起こりうるすべての場合の数を求めるのは、比較的簡単です。
与えられた条件を満たす場合の数を求めるのが大変なわけですが、この場合、カードの左から並べていく方法と、右から並べていく方法がありますが、どうやら右から並べていった方が、シンプルに考えられそうですね。

Challenge!