問題182 ケーキ屋さんの問題
あるケーキ屋さんで、1個300円 (原価150円) のケーキを作って販売しています。 過去100日間での販売個数の実績は次の表のとおりでした。
| 1日の販売個数 | 90 | 100 | 110 | 120 | 130 |
|---|---|---|---|---|---|
| 日数 (過去100日のうち) | 20 | 40 | 20 | 10 | 10 |
すなわち、1日で90個のケーキが売れたのは過去100日のうち20日、
100個のケーキが売れたのは (過去100日のうち) 40日、
110個売れたのは (過去100日のうち) 20日、
120個売れたのは (過去100日のうち) 10日、
130個売れたのは (過去100日のうち) 10日でした。
今後もこの割合で売れると予測しています。
このとき、利益が最も多くなるのは、
1日何個のケーキを作ればよいでしょうか。
ただし、ケーキは10個単位で販売するとします。
(選択肢)
1.90個 2.100個 3.110個 4.120個 5.130個
問題の出典
解答
〜到着順にご紹介します〜
解答・その1
(ペンネ−ム:スモークマン)
売り上げを10x とすると...
x は9以上になるはず...
たとえば...x=10 のとき...
9個しか売れなかったら...(10-9)=1個分はチャラになる...^^;
つまり...9-(10-9)=8個分の売り上げ...
x=10...のとき...
(9-(10-9))*2+10*(4+2+1+1)=16+80=96
x=11...
(9-(11-9))*2+(10-(11-10))*4+11*(2+1+1)=14+36+44=94
x=12...
(9-(12-9))*2+(10-(12-10))*4+(11-(12-11))*2+12*(1+1)=12+32+20+24=88
x=13...
(9-(13-9))*2+(10-(13-10))*4+(11-(13-11))*2+(12-(13-12))+13=10+28+18+11+13=80
ちなみに...
x=9...
9*(2+4+2+1+1)=90
予想通り...100個のときの売り上げが最大♪
もっと簡単にできるのかしら...?
解答・その2
(ペンネ−ム:haya)
答:2.100個 です。
【解き方】
ケーキの作成個数を増やせば、ある個数までは売り上げ増となるが、
作り過ぎによる売れ残りが収益を下げる。
一日にケーキが売れる個数の確率は下のTable1の如し。
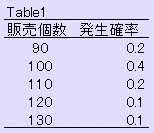
この確率でのケーキの作成個数と損益の期待値の式はTable2の如し。

上の結果はTable3となる。
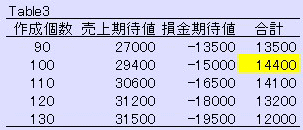
期待値が一番大きくなるのは2.の100個作成のケースで、この時の儲けは \14,400 となる。
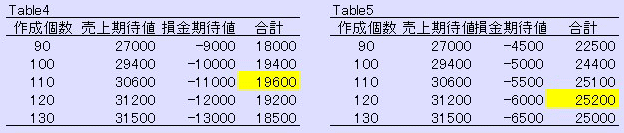
PS: 原価が高過ぎで、余り実的でないというのが実感です。 原価を \100 にするとTable4、\50 ではTable5 となります。現実にはこちらでしょう。
解答・その3
(ペンネ−ム:オヤジ)
100日間の販売した利益を考える。
(1)1日90個作った場合
生産コスト
90個×150円×100日=135万円
売り上げ
90個×300円×100日=270万円
利益
270万円−135万円=135万円
(2)1日100個作った場合
生産コスト
100個×150円×100日=150万円
売り上げ
100個×300円×80日=240万円
90個×300円×20日= 54万円
従って
240万円+54万円=294万円
利益
294万円−150万円=144万円
(3)1日110個作った場合
生産コスト
110個×150円×100日=165万円
売り上げ
110個×300円×40日=132万円
100個×300円×40日=120万円
90個×300円×20日= 54万円
従って
132万円+120万円+54万円=306万円
利益
306万円−165万円=141万円
(4)1日120個作った場合
生産コスト
120個×150円×100日=180万円
売り上げ
120個×300円×20日= 72万円
110個×300円×20日= 66万円
100個×300円×40日=120万円
90個×300円×20日= 54万円
従って
72万円+66万円+120万円+54万円=312万円
利益
312万円−180万円=132万円
(5)1日130個作った場合
生産コスト
130個×150円×100日=195万円
売り上げ
130個×300円×10日= 39万円
120個×300円×10日= 36万円
110個×300円×20日= 66万円
100個×300円×40日=120万円
90個×300円×20日= 54万円
従って
39万円+36万円+66万円+120万円+54万円=315万円
利益
315万円−195万円=120万円
従って (1)〜(5)より
∴ 100個
解答・その4
(ペンネ−ム:のっこん)
便宜上、100日間を10日間に縮めて考える
すなわち、10日のうち2日は90個
4日は100個
2日は110個
1日は120個
1日は130個 売れたことにする
売値300円、原価150円だから
1個売れると150円もうけ、1個売れ残ると150円損をする
つまり、a個売れると150a円もうけ
b個売れ残ると150b円損をする
利益は150a-150b=150(a-b)で計算される
従って(a-b)の大小を比較すればよい
(1)1日に90個作った時
売れ残る日はないからb=0、a=90・10=900
a-b=900
(2)1日に100個作った時
10個売れ残る日が2回あるからb=20、a=100・10-20=980
a-b=960
(3)1日に110個作った時
10個売れ残る日が4回、20個売れ残る日が2回あるから
b=80、a=110・10-80=1020
a-b=940
(4)1日に120個作った時
10個売れ残る日が2回、20個売れ残る日が4回、30個売れ残る日が2回あるから
b=160、a=120・10-160=1040
a-b=880
(5)1日に130個作った時
10個売れ残る日が1回、20個売れ残る日が2回、30個売れ残る日が4回、
40個売れ残る日が2回あるから b=250、a=130・10-250=1050
a-b=800
(a-b)は1日に100個作った時に最大となるから 利益を最も多くするには1日に100個のケーキを作ればよい
※1日平均では105個売れるから、1日100個でも110個でも同じかと思いましたが、違うんですねえ〜
解答・その5
(ペンネ−ム:転位反応)
(1)販売利益は150円/個、売れ残りによる損失は150円/個である。
(2)1日当たりの平均販売個数は、105個である。
90×0.2+100×0.4+110×0.2+120×0.1+130×0.1 =105
(1)(2)より、できるだけ売れ残り個数を少なくして、販売個数を増やすことが利益の最大化につながるので、
1日当たりの平均販売個数である105個に近い、100個、または、110個が解の候補として考えられる。
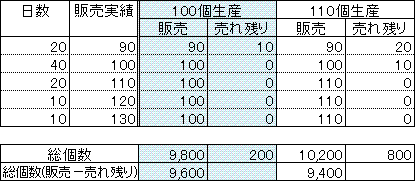
ケーキ1個当たりの販売利益と損失の絶対値は等しいので、総販売個数から総売れ残り個数を差し引いた数
をもとに利益最大のケースを選択できる。
検証の結果は以下の通り。
よって、選択肢2の100個が求める解である。
解答・その6
(ペンネ−ム:ちょろんは太太)
ケーキを x個作ったときの利益の期待値 y を考える。
x<90の場合、すべての日ですべて販売されるので、
y=300×x-150×x=150×x

期待値 y は、x=100で、増加から減少に転じる。
(答え) 2.100個
解答・その7
(ペンネ−ム:迷子の雄猫)
ある日の売り上げは(販売個数 と 製造個数 の小さいほう)×300円
製造原価は(製造個数)×150円
利益は(売り上げ−製造原価)
計算すると以下の表のようになる。
| 売り上げ/製造 | 90 | 100 | 110 | 120 | 130 |
|---|---|---|---|---|---|
| 90 | 13,500 | 12,000 | 10,500 | 9,000 | 7,500 |
| 100 | 13,500 | 15,000 | 13,500 | 12,000 | 10,500 |
| 110 | 13,500 | 15,000 | 16,500 | 15,000 | 13,500 |
| 120 | 13,500 | 15,000 | 16,500 | 18,000 | 16,500 |
| 130 | 13,500 | 15,000 | 16,500 | 18,000 | 19,500 |
それぞれに過去の販売実績(日数)を加味して・・・
| 製造個数 | 90 | 100 | 110 | 120 | 130 | |
|---|---|---|---|---|---|---|
| 販売個数 | 日数 | |||||
| 90 | 20 | 270,000 | 240,000 | 210,000 | 180,000 | 150,000 |
| 100 | 40 | 540,000 | 600,000 | 540,000 | 480,000 | 420,000 |
| 110 | 20 | 270,000 | 300,000 | 330,000 | 300,000 | 270,000 |
| 120 | 10 | 135,000 | 150,000 | 165,000 | 180,000 | 165,000 |
| 130 | 10 | 135,000 | 150,000 | 165,000 | 180,000 | 195,000 |
| 利益合計 | 1,350,000 | 1,440,000 | 1,410,000 | 1,320,000 | 1,200,000 | |
よって、数学の問題として考えると
最も利益が大きくなるのは毎日100個作ったときの1,440,000円である。
が、現実問題として考えるなら毎日110個は作るべきだろう。
100日のうち40日、70人ものお客を逃すのは痛いと思うからである。
100日で30,000円の利益が減少するが、一日あたりでは300円で、ケーキ1個分にしかならない。
あまったケーキは近くの施設に寄付しちゃえば社会貢献にもなるし、
買いに来て売切れていたお客のうち一部は二度と来なくなるだろうから、次
の100日で売れた実績が90個:100個:110個:120個:130個=30:40:20:10:0
になるリスクもあるし。
解答・その8
(ペンネ−ム:浜田 明巳)
製造個数で場合分けする.
i). 90個の場合,利益は,
90×300×(20+40+20+10+10)/100−90×150
=27000−13500=13500(円)
ii). 100個の場合,利益は,
90×300×20/100+100×300×(40+20+10+10)/100−100×150
=5400+24000−15000=14400(円)
iii). 110個の場合,利益は,
90×300×20/100+100×300×40/100+110×300×(20+10+10)/100−110×150
=5400+12000+13200−16500=14100(円)
iv). 120個の場合,利益は,
90×300×20/100+100×300×40/100+110×300×20/100+120×300×(10+10)/100−120×150
=5400+12000+6600+7200−18000=13200(円)
v). 130個の場合,利益は,
90×300×20/100+100×300×40/100+110×300×20/100+120×300×10/100+130×300×10/100−130×150
=5400+12000+6600+3600+3900−19500=12000(円)
故に最大の利益を上げるには,100個製造すればよい.選択肢は2である.
エクセルのマクロでは,次の通り.
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Dim j As Integer
Dim jj As Integer
Cells(1, 1).Value = "個数"
Cells(1, 2).Value = "利益"
For j = 1 To 5
Cells(j + 1, 1).Value = kosuu(j)
Cells(j + 1, 2).Value = 0
For jj = 1 To 5
Cells(j + 1, 2).Value = Cells(j + 1, 2).Value + (kosuu(Application.Min(j, jj)) * 300 - kosuu(j) * 150) * nissuu(jj) / 100
Next jj
Next j
Cells(7, 1).Value = "最大値"
Cells(7, 2).Value = "=MAX(B2:B6)"
For j = 2 To 6
If Cells(j, 2).Value = Cells(7, 2).Value Then
Range("B" & j).Select
End If
Next j
End Sub
Private Function kosuu(ByVal n As Integer) As Long
Select Case n
Case 1
kosuu = 90
Case 2
kosuu = 100
Case 3
kosuu = 110
Case 4
kosuu = 120
Case Else
kosuu = 130
End Select
End Function
Private Function nissuu(ByVal n As Integer) As Integer
Select Case n
Case 1
nissuu = 20
Case 2
nissuu = 40
Case 3
nissuu = 20
Case 4
nissuu = 10
Case Else
nissuu = 10
End Select
End Function
解答・その9
(ペンネ−ム:T_Tatekawa)
100日間の利益で比較する.売ると利益が150円,売れ残ると損失が150円.
まず1日90個作る時の利益は,
90*(20+40+20+10+10)*150=1,350,000円
1日100個作る事にすると,80日は完売し,20日は10個売れ残る.
すると利益は
(100-90)*150*80 - 150*20*10 = 90,000円
増える.
1日110個作る事にすると,売れる個数は 40*10=400 個増えるが, 売れ残りが 60*10=600 個増えるので損失が増える.
1日120個作ると,売れる個数はさらに 20*10=200 個増えるが,売れ残りが 800個増える.
1日130個作ると,売れる個数が100個増え,売れ残りが 900個増える.
よって,利益がもっとも多くなるのは1日100個作るとき.
解答・その10
(ペンネ−ム:次郎長)
毎日90個作ったときは、原価150*90*100=135万
売上は300*90*100=270万 利益135万
毎日100個作ったときは、原価150*100*100=150万
売上は300*100*80+300*90*20=294万 利益144万
毎日110個作ったときは、原価150*110*100=165万
売上は300*110*40+300*100*40+300*90*20=306万 利益141万
毎日120個作ったときは、同様に 利益132万
毎日130個作ったときは、同様に 利益120万
となり、「毎日100個作ったときの利益が最大」となります。
解答・その11
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
答え 100個作った時が一番利益があります。
○ 一日90個作った場合の販売個数と利益
90×100=9000個
売上金 9000個×300円=2700000円
原 価 90個×100日×150円=1350000円
90個作る時の利 益 1350000円
○ 一日100個作った場合の販売個数と利益
90×20+100×80=9800個
売上金 9800×300円=2940000円
原 価 100個×100日×150円=1500000円
100個作る時の利 益 1440000円
○ 一日110個作った場合の販売個数と利益
90×20+100×40+110×40=10200個
売上金 10200個×300円=3060000円
原 価 110個×100日×150円=1650000円
110個作る時の利 益 1410000円
○ 一日120個作った場合の販売個数と利益
90×20+100×40+110×20+120×20=10400個
売上金 10400個×300円=3120000円
原 価120個×100日×150円=1800000円
120個作る時の利 益 1320000円
○ 一日130個作った場合の販売個数と利益
90×20+100×40+110×20+120×10+130×10=10500個
売上金 10500個×300円=3150000円
原 価 130個×100日×150円=1950000円
130個作る時の利 益 1200000円
従って一日100個を作った時が一番利益があります。
解答・その12
(ペンネ−ム:まめ)
1日90個生産時は、生産した分全てが毎日売り切れるので、
製造原価=90×100×150=135万円=利益
1日100個生産時は、
製造原価=100×100×150=150万円
90個売れる日が20日、100個売れる日が80日あるので、
売り上げ=(90×20+100×80)×300=294万円
よって、
利益=294‐150=144万円
以下同様に、
110個生産時
利益=141万円
120個生産時
利益=132万円
130個生産時
利益=120万円
以上より、1日100個生産した場合の利益144万円が最多となる。
答えは「2」。
解答としては以上です。
普通に、売れる個数の最頻値が答えなので、
逆に本当に正しいのか不安になってしまいます。
あえてポイントを探るとすると、
110個売れる日に100個しか作ってなくてもその100個は必ず売れる、
ということでしょうか。
ただ、ビジネスの世界では、100個しかなくて110個売れる日に変えなかった1人、
10日間で述べ20人の人が他店に流れる可能性も考慮することも必要かも。
120個や130個の日も合わせると述べ70人のお客さんを手放すことになるかも。
130個以上は売れないって予め分かっているのならば、
130個作って、売れ残りそうな日は値引きしてでも売った方が良かったりして。
解答・その13
(ペンネ−ム:Ryu1128)
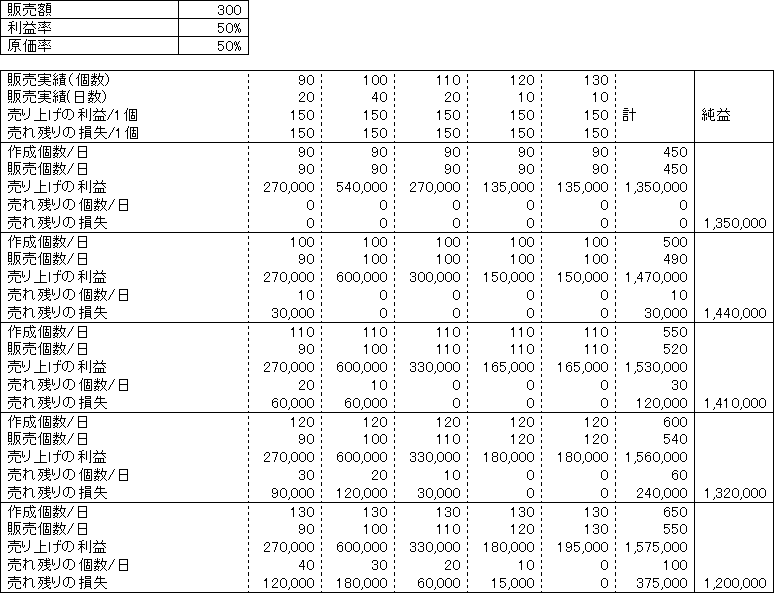
上記より100個・・・回答2
解答・その14
(ペンネ−ム:kazz)
計算を簡単にするため、原価a円、定価2a円(実際はa=150)とします。
- 1個当たりの利益は2a-a=a円なので、作ったケーキがすべて売れれば
(見込みの利益)=(作った個数)×a 円 ・・・(1)
となります。 - しかし、実際には1日の販売個数以上作ることがあるので、多く作りすぎた分は売れ残りとなり、損失が生じます。
もともと売れると見込んだ2a円が0円となるので
(損失)=(売れ残りの数)×2a 円 ・・・(2)
となります。 -
実際の利益は(1)-(2)で求めることができます。
それぞれの損失を求めます。
90個/日→0 円
100個/日→(10×20)×2a=400a 円
110個/日→(20×20+10×40)×2a=1600a 円
120個/日→(30×20+20×40+10×20)×2a=3200a 円
130個/日→(40×20+30×40+20×20+10×10)×2a=5000a 円
よって、それぞれの実際の利益を計算すると、
90個/日→90×100×a-0=9000a 円
100個/日→100×100×a-400a=9600a 円
110個/日→110×100×a-1600a=9400a 円
120個/日→120×100×a-3200a=8800a 円
130個/日→130×100×a-5000a=8000a 円
したがって、*100個/日*のとき利益が最大になります。
解答・その15
(ペンネ−ム:夜ふかしのつらいおじさん)
次のようにそれぞれの個数つくったときに上がる利益を比べると、1日に100個作るときが利益の最大です。
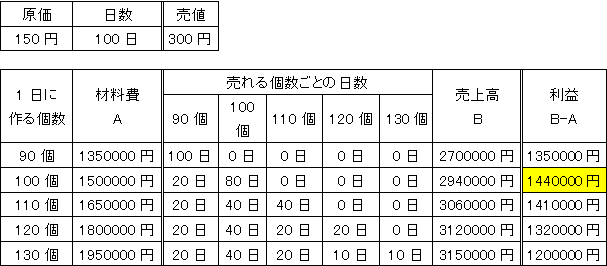
解答・その16
(ペンネ−ム:三角定規)
例えばケーキを 110 個作った場合,販売実績によれば,90 個売れる可能性が 20%,
100 個売れる可能性が 40%,110 個すべて売れる可能性が 40%だから,販売見込みは
90×0.2+100×0.4+110×0.4=102 個
である。
同様にして,90 個〜130 個すべての場合について,販売見込と利益は表のようになるから,利益が最も多くなるのは,
2.100 個 … [答]
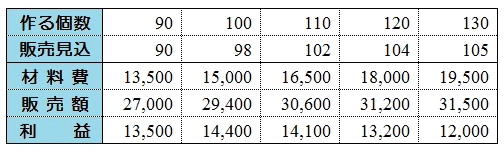
コメント
ケーキが売れれば利益が出るが、売れ残れば原価分だけ損をします。 販売実績に基づいて、シミュレーションをすることになり、 そうすると、毎日100個販売するケースが最も利益が大きいことがわかります。 この問題えは、シンプルにモデル化されていますが、 実際の場面では、もっと複雑な要因や、販売戦略が関係するのでしょうね!
 top
top