問題181　２０１２年の問題

2012人の男子と2012人の女子が集まってプレゼント交換をする。男子は花束を、女子はチョコレートを１つずつプレゼントとして用意する。全員で円形に並んで内側を向き、１回合図があるごとに同時にプレゼントを右隣の人に渡す。男子はチョコレートを、女子は花束を受け取ったらその時点で円から抜けることにする。
このとき、全員が円から抜けるまでに必要な合図の回数は最大で何回でしょうか。

問題の出典

ジュニア数学オリンピック　2003-2008
数学オリンピック財団　編
第６回日本ジュニア数学オリンピック

解答

～到着順にご紹介します～

解答・その1

（ペンネ－ム：杖のおじさん）

答え　　２０１２回です。
最大の合図の回数になるように並ぶには下の図のようになります。

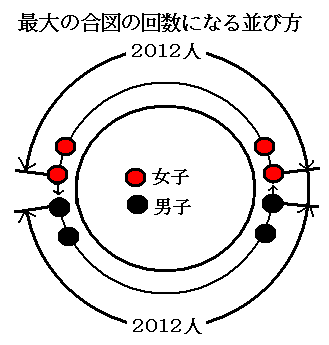
男子と女子が円の半分を境にして囲むように並びます。１回の合図で右隣りにプレゼントを渡しますので左側の男子から渡された女子１一人と左側の女子から渡された男子一人が抜けて行く事になります。従って、全員が抜けるのは２０１２回となります。

解答・その2

（ペンネ－ム：迷子の雄猫）

答えは2012回です。
円形に男女が並んでいるのだから、男子の右側に女子が並んでいる位置が必ずあるはずである。よって合図ごとに必ず最低でも一人の女子が抜ける。
また、2012人の男子と2012人の女子が全員で円形に並んで、男子は女子の、女子は男子のプレゼントを受け取ったらその時点で円から抜けるのだから、必ず男女同数が円から抜けることになる。
なぜなら、まず、初期状態が男女同数でプレゼントも男女同数である。円に残っている男子は男子の、女子は女子のプレゼントを持っているはずである。円から抜けた男子は女子の、女子は男子のプレゼントを持っているはずである。
合図の後で円に残っている男女が同数ではなかった、仮に男子のほうが多いと仮定すると
　円に残っている男子＞円に残っている女子
　円から抜けた女子＞円から抜けた男子
が成り立ち、円に残っている男子の持っている男子のプレゼント＞円に残っている女子の持っている女子のプレゼント円から抜けた女子の持っている男子のプレゼント＞円から抜けた男子の持っている女子のプレゼントが成り立つので、全体では
　男子のプレゼント＞女子のプレゼント
が成立してしまう。これは矛盾。
よって、合図ごとに最低一組の男女が抜けるので、合図の必要回数は最大でも2012回。
円の左半分が男子だけ、右半分が女子だけという風に並ぶと、男子の右側に女子が並んでいるのも女子の右側に男子が並んでいるのも１箇所だけであるので、合図ごとに男女各１人しか円から抜けないので、この場合には合図が2012回必要となる。
Ｑ．Ｅ．Ｄ．

解答・その3

（ペンネ－ム：スモークマン）

男女が隣り合うポイントが一番少ないときを考えれば交換されることが一番少ないので...
つまり...２カ所の場合...(2012人同士の塊で円状に並ぶ...個人的には両手に花状態がいいなぁ...^^)...
このとき１回の合図で２交換され...2人が駆け落ちできる ^^
けっきょく...2012*2/2=2012 回の合図が必要♪...真ん中に座りたくない...^^;

解答・その4

（ペンネ－ム：haya）

答：最大の回数は 2012 です。

【解き方】
人の環の一部で同性者が続く部分を「区間」と呼ぶと、
　1.. 区間は必ず偶数個発生する（一人でも1区間として）
　2.. 区間の中ではプレゼント交換成功による人の抜けは発生しない
　3.. 抜けは区間の境界で起こる
1.より区間の数は 2n とでき、2.、3.より、その時抜ける人数は 2n となる。

上を自明として、男女が一人ずつ互い違いに並べば、これは n=2012 相当で、一回の合図で全員が円を抜けることができる。
逆にこの抜ける効率を最低にするには、n=1 とすべきで、男女を別々に連続して並べること。
こうすれば1回の合図で男女各1名、都合2名だけが抜ける。
合図の回数を t として、全員が抜けるには、
　　2012*2 - 2t = 0
　　t = 2012
よって、最大の回数は 2012 となる。

解答・その5

（ペンネ－ム：T_Tatekawa）

簡単のため，まず男女4人ずつが並んでいる場合を考える．
男子をM，女子をWと表す．
交互に並んでいれば1回の合図で全員が抜けるが，男子，女子それぞれが固まっていると，合図では男女の入れ替わりのところしか抜けない．
円を開いて書いて行くと，

　　0: MMMMWWWW
　　1:  MMM WWW
　　2:   MM  WW
　　3:    M   W

で，4回目で全員が抜ける．
この考えを男子2012人，女子2012人の場合に拡張すると，全員が円から抜けるまでに必要な合図の回数は最大で 2012回．

解答・その6

（ペンネ－ム：転位反応）

問題に示された合図の回数を最大にするには、一回の合図で円から離脱する人数を最少にすれば良く、そのためには、隣に異性が並ぶような並び方を最少にすれば良い。
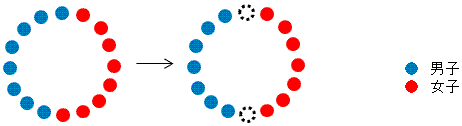
例えば、男子８人、女子８人のケースを例に示すと、下図の並び方が最少になって、一回目の合図で円から離脱する人数は、男子１人、女子１人の計２人である。
２回目の合図でも、男女、各１人が離脱し、以降、全員が離脱するまで同じことの繰り返しとなる。
よって、男女、各２０１２人の場合でも本質的に同じなので、最大の回数は２０１２回になる。

解答・その7

（ペンネ－ム：オヤジ）

出来るだけ同性から、プレゼントを受け取った方が良いから。
男子2012人と女子2012人の２つのグループの固まりの4024人の円を作れば良い。
１回の合図で男子2012人の左端の男子が、女子2012人の右端の女子からチョコレートを受け取り、女子2012人の左端の女子が、男子2012人の右端の男子から花束を受け取り、男子女子各一人の合計２人が円を抜ける。
以下同様に１回の合図で男子女子各一人の合計２人が円を抜ける。
従って、全員が円から抜けるまでに必要な合図の回数は４０２４÷２＝２０１２
　　　∴　２０１２回

解答・その8

（ペンネ－ム：のっこん）

（男女が隣り合っている個所の数）＝（円から抜ける人の数）である
だから例えば男女が交互に並んだ時は、1回の合図で全員が円から抜ける
合図の回数を多くするには、男女が隣り合っている個所をなるべく少なくすればよい
隣り合っている個所が0箇所あるいは1箇所ということはあり得ないから
隣り合っている個所の最小は2箇所である
この時は1回の合図で2人が円から抜ける
隣り合っている個所が2箇所というのは次のような場合である

　　　　　　　　　　　　　　　M1
　　　　　　　　　　　F2012　　　M2
　　　　　　　　　F2011　　　　　　　M3
　　　　　　　　　・・・　　　　　　　　・・・
　　　　　　　　　　F3　　　　　　　M2011　　　　　　　　
　　　　　　　　　　　　 F2　　　M2012
　　　　　　　　　　　　　　　F1

この時は1回目の合図でM2012とF2012の2人が抜け
2人が抜けた後も
男女が隣り合っている個所は相変わらず2個所だから
2回目の合図でM2011とF2011の2人が抜け
　　　・・・・・・・・・・・
1回の合図ごとに2人が抜けていくから
必要な合図の回数の最大は 2012×2÷2=2012（回）

解答・その9

（ペンネ－ム：浜田　明巳）

　ｎ人の男子とｎ人の女子が集まってプレゼント交換するとする．
i). ｎ＝１のとき，
　　男１
　　↓↑
　　女１
　故に１回の合図で終わる．

ii). ｎ＝２のとき，
　　男２←男１　　　男２
　　↓　　　↑　⇒　↓↑
　　女１→女２　　　女２

　　女１←男１
　　↓　　　↑
　　男２→女２
　故に最大２回の合図で終わる．

iii). ｎ＝３のとき，
　　男３←男２←男１　　　男３←男２　　　男３
　　↓　　　　　　↑　⇒　↓　　　↑　⇒　↓↑
　　女１→女２←女３　　　女２→女３　　　女３

　　女１←男２←男１　　　男２
　　↓　　　　　　↑　⇒　↓↑
　　男３→女２→女３　　　女３

　　男２←女１←男１
　　↓　　　　　　↑
　　女２→男３→女３
　故に最大３回の合図で終わる．

　どのように並んだとしても，少なくとも１人の男子の右に女子が，少なくとも１人の女子の右に男子が座っている．したがって１回の合図で少なくとも男女１人ずつ抜ける．つまりｎ人の場合，最大でｎ回の合図で全員抜ける．上例と同様に，男子ｎ人，女子ｎ人がそれぞれまとまって並べば，ｎ回の合図で終わるので，ｎ回の場合が確かに存在し，並び方はこの場合に限る．
　ｎ＝２０１２のとき，最大２０１２回の合図で終わる．このときの並び方は男２０１２人，女２０１２人がまとまって座る．

解答・その10

（ペンネ－ム：次郎長）

答え　2012回

男女男女の順に座っている場合は、1回で全員が抜けることが出来ますが、
男子2012人、女子2012人が向かい合った形で輪になれば、
1回の合図で抜けることが出来るのは男女共に左端の一人のみ。
1回の合図で男女各2011人が残る。
2回の合図で男女各2010人が残る。
・
・
2011回の合図で男女各1人が残り、
2012回目の合図で、最後の2人が抜ける。
つまり、2012回

解答・その11

（ペンネ－ム：夜ふかしのつらいおじさん）

花束が一番長く受け渡しされる場合を考えます。
その花束は女子に渡った途端、円から抜けてしまいます。
そこでなるべくながく男子に続けて渡される場合を考えれば良いことになります。
その花束の右側に2011人の男子がいれば2011回は受け渡しが続きます。
その時点ではもう男子はいないので最後の女子に渡ってその花束は円から消えてしまいます。
合図の回数は2012回です。

解答・その12

（ペンネ－ム：まめ）

考えるまでもなく答えは2012回、なんですけど・・・。
一応それなりに問題の意図からして、それが唯一解であることを示す必要があるのかなぁ・・・。

最大の回数を考えればよいから、まずは1回の操作でできるだけ数が減らないパターンを考えて輪を作ってみる。つまり、男子の右隣に男子、女子の右隣に女子と並べることを考えると、 2012人の男子、2012人の女子が連続して並ぶパターンとなる。このパターンでは当然、1回目の交換で各1人の男女が抜け、次に各2011人の連続した男女の輪となる。以下この操作が2011回繰り返されるから、この場合、2012回で男女がいなくなる。

次に、1回の操作で抜ける男子、女子の最低人数を考える。ある交換の際にM人の男子からm人、F人の女子からf人抜けたとする。この交換で減ったチョコレートはm個であり、このm個が女子に渡ったことで女子がf人減った訳であるから、m＝f。
必ず男女は同じ数ずつ減ることが分かるから、ある交換の後に残る男女の数も等しい。つまり男子だけ、女子だけが残ることはありえない

結局、どの交換の後でも必ず男子、女子が同数混じった輪になっている。仮にX人の男子、女子がそれぞれ連続した輪になったとしても、 X番目の男子の右隣には女子がいるし、X番目の女子の右隣には男子がいる。そのような男子、女子は次の交換で必ず抜け、その1組が唯一の最低値と言える。

よって各2012人の男女から最大でかかる交換の回数は、毎回1組ずつ抜ける場合であり、2012回。

解答・その13

（ペンネ－ム：三角定規）

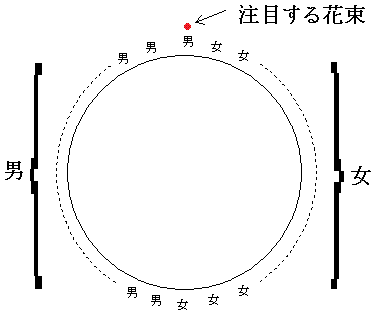
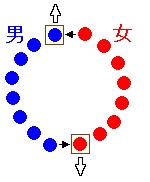
合図の回数が最大になるのは，１回に抜ける数が最小＝男女が隣り合っている箇所が最小の場合で，それは添付図のように，男女が完全に別々に分かれてしまった場合である。
この場合，１回の合図で円から抜けることができるのは男女が隣り合っている２ヶ所の２人のみで，この２人が抜けた後，隣り合う男女はまた２組である。
複数の男女が円形に並ぶ場合隣り合う男女は最低２ヶ所だから，合図の最大数は上のように男女が完全に分かれる場合で，それは
　2012×2／2＝2012 回　…［答］

解答の公開が遅くなってしまい、申し訳ありませんでした。

2012人の男子と2012人の女子が円形に並んでいると、必ず男女が隣り合う箇所が少なくとも２か所存在します。一つは男子の右隣に女子、もう一つは女子の右隣に男子です。したがって、合図があると、少なくとも男子一人、女子一人が円から抜けることになります。また、円から抜ける男女の数は同数です。つまり円に残る男女の数も同数です。以下、同じことが繰り返されますから、最大2012回の合図で、必ず全員が円から抜けることになります。
実際、男子が2012人連続し、女子が2012人連続して並び、円を作るような場合を考えれば、2012回の合図が必要となりますので、2012回が最大となります。

Challenge!