問題179　平均の問題

０以上１００００以下の整数の中で、１０進法で表記したときに１が現れないようなものすべての平均を求めよ。

問題の出典

数学オリンピック
日本評論社
第20回日本数学オリンピック予選(2010年)

解答

～到着順にご紹介します～

解答・その1

（ペンネ－ム：浦岡）

便宜上、題意のような整数を「００００、０００２、０００３、…、０００９、００２０、００２２、…、９９９９」という風に０を補い、すべて４桁にして扱う。
つぎに、これらが全部でｍ個であるとすると、千、百、十、一のそれぞれの位に「０、２、３、…、９」がｍ/９回の同回数で現れることから
　（合計） = １０００（０+２+３+…+９）ｍ/９ + １００（０+２+３+…+９）ｍ/９ + １０（０+２+３+…+９）ｍ/９
　　　　　　　　　+（０+２+３+…+９）ｍ/９
　　　　　 = １１１１×４４ｍ/９
　　　　　 = ４８８８４ｍ/９
∴（平均） = ４８８８４ｍ/９ ÷ ｍ = *４８８８４/９* …（答）

解答・その2

（ペンネ－ム：T_Tatekawa）

0以上9以下の場合，1以外の数の平均を取る．
　　44/9
0以上99以下の場合，1を含まない整数の数は
　　100- 10*2 + 1 = 81個
十の位と一の位を分けて考える．
十の位，一の位それぞれで平均を取る．
どちらも，1以外の数が9個ずつ現れるので，
0以上99以下の整数で1が現れないもの全ての平均は
　　(44 * 10 * 9 + 44 * 9)/81 = 484/9
同様に考えて，0以上9999以下で1を含まない整数の数は
　　9*9*9*9=6561個
四桁それぞれについて，現れる数を考える．1以外の数が
　　9*9*9=729個
現れる．0以上9999以下で1が現れない整数の合計は
　　(44 * 1000 + 44 * 100 + 44 * 10 + 44 * 1) * 729=48884*729
10000は1が現れるので除外．よって平均は
　　48884*729/6561= 48884/9

解答・その3

（ペンネ－ム：夜ふかしのつらいおじさん）

1を使わないので、{0,2,3,4,5,6,7,8,9}の9個の数字を使ってできる数を考えます。
0を含めて、10000未満のそのような数は、4桁を考えればよいので、　　9×9×9×9＝9⁴＝6561個
です。そのような数の合計を位ごとに考えます。
　　0＋2＋3＋4＋5＋6＋7＋8＋9＝44
です。一の位に{0,2,3,4,5,6,7,8,9}は、周期的に6561÷9＝729回現れます。
1つの数字が十の位は9個、百の位は9²個、千の位は9³個、続けて現れます。
現れ方は異なっても{0,2,3,4,5,6,7,8,9}の合計の現れる総数は同じです。よって、
　　一の位は、44×729＝32076
　　十の位は、10×44×729＝320760
　　百の位は、100×44×729＝3207600
　　千の位は、1000×44×729＝32076000
合計は、(1＋10＋100＋1000)×44×729＝1111×44×729＝35636436
ゆえに平均は、35636436÷6561＝5431.5555････（＝5431+5/9 ＝48884/9）

解答・その4

（ペンネ－ム：のっこん）

10000は1が現れているので除外して考える
1を除く0から9までの和は44
0から9999までの和は49995000

0以上9999以下の整数において
1が現れないのは
○○○○においてどの○も
1を除く0から9までの時
よってその個数は9⁴＝6561

○○○○において1が4個あるのは1111の時
○○○○において1が3個あるのは
　(1)111○において○が1を除く0から9の時
　(2)11○1において　　　　　〃
　(3)1○11において　　　　　〃
　(4)○111において　　　　　〃
　(1)、(2)、(3)、(4)ともそれぞれ9通りあるから
　２.に該当するすべての数の和は
　1000（3・9＋44）＋100（3・9＋44）＋10（3・9＋44）＋3・9＋44＝71・1111＝78881
○○○○において1が2個あるのは
　(1)11○○において○が1を除く0から9の時
　(2)1○1○において　　　　　〃
　(3)1○○1において　　　　　〃
　(4)○11○において　　　　　〃
　(5)○1○1において　　　　　〃
　(6)○○11において　　　　　〃
　(1)、(2)、(3)、(4)、(5)、(6)ともそれぞれ9²＝81通りあるから
　３.に該当するすべての数の和は
　1000（3・81＋3・9・44）＋100（3・81＋3・9・44）＋10（3・81＋3・9・44）＋3・81＋3・9・44＝1431・1111＝1589841
○○○○において1が1個あるのは
　(1)1○○○において○が1を除く0から9の時
　(2)○1○○において　　　　　〃
　(3)○○1○において　　　　　〃
　(4)○○○1において　　　　　〃
　(1)、(2)、(3)、(4)ともそれぞれ9³＝729通りあるから
　４.に該当するすべての数の和は
　1000（729＋3・81・44）＋100（729＋3・81・44）＋10（729＋3・81・44）＋729＋3・81・44＝11421・1111＝12688731

1が現れるすべての数の和は
1111＋78881＋1589841＋12688731＝14358564

1が現れないすべての数の和は
49995000－14358564＝35636436

よって 1が現れないすべての数の平均＝35636436/6561＝48884/9＝5431.5555・・・

解答・その5

（ペンネ－ム：マシャ）

各桁に0, 2, 3,～9までが入る全ての組み合わせを考えればいいので,その平均は44/9になります.
桁は1000, 100, 10, 1があるので, 全体の平均は
　　44/9*1111=48884/9≒5431.56
です.

解答・その6

（ペンネ－ム：haya）

答： 5431.555… = 35636436 / 6561

【解き方】
逆に桁に1を含む整数について考える。　 4桁の整数の4桁目(先頭桁)を見ると、1は全て含まれるから1000個。　 2～9の数字については、1を全く含まない整数は排除されるから数が減る。 3桁全て1を含まない組合せは、
　　1000-9³ = 1000 - 729 = 271
より、各271個。　これは10000未満のその他の位の数字の出現頻度についても同様である。つまり、10000以下の整数の各桁の数字の出現頻度は下図となる。

上の表を計算して、桁に少なくとも1個1を含む整数の総和は

一方、全体の総和は、　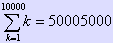　　より、求める1を含まない整数の総和は、
　　50005000-14368564=35636436
その個数は、4桁とも1を含まない組合せだから、
　　9⁴ = 6561
通り。よって求める解は、
　　5431.555… = 35636436 / 6561
となる。

解答・その7

（ペンネ－ム：浜田　明巳）

２０１０年数学オリンピック予選の問題２からですね．
総和の１の位の数は，
　　０＋２＋３＋４＋５＋６＋７＋８＋９＝４４
の和となっている．
他の３桁を考えると，この数の９^３倍．
同様に他の桁も
　　４４×９^３
となっているので，総和は，
　　４４×９^３×(１０００＋１００＋１０＋１)＝４４×９^３×１１１１
この数の総数は，
　　９^４
故に平均は，
　　４４×９^３×１１１１／９^４＝４４×１１１１／９＝４８８８４／９
エクセルのマクロでは，以下の通り．

Option Explicit
Sub Macro1()
    Sheets("Sheet1").Select
    Cells(1, 1).Value = 0
    Cells(1, 2).Value = 0
    Dim a As Integer
    Dim b As Integer
    Dim c As Integer
    Dim d As Integer
    Dim g As Long
    For a = 0 To 9
      If a <> 1 Then
        For b = 0 To 9
          If b <> 1 Then
            For c = 0 To 9
              If c <> 1 Then
                For d = 0 To 9
                  If d <> 1 Then
                    Cells(1, 1).Value = Cells(1, 1).Value + (a * 1000 + b * 100 + c * 10 + d)
                    Cells(1, 2).Value = Cells(1, 2).Value + 1
                    Cells(Cells(1, 2).Value, 4).Value = a
                    Cells(Cells(1, 2).Value, 5).Value = b
                    Cells(Cells(1, 2).Value, 6).Value = c
                    Cells(Cells(1, 2).Value, 7).Value = d
                    Range("D" & Cells(1, 2).Value).Select
                  End If
                Next d
              End If
            Next c
          End If
        Next b
      End If
    Next a
    g = GCM(Cells(1, 1).Value, Cells(1, 2).Value)
    Cells(2, 1).Value = Cells(1, 1).Value / g
    Cells(2, 2).Value = Cells(1, 2).Value / g
    Range("A2").Select
End Sub
Private Function GCM(ByVal a As Long, ByVal b As Long) As Long
    If b = 0 Then
      GCM = a
    Else
      GCM = GCM(b, a Mod b)
    End If
End Function

解答・その8

（ペンネ－ム：スモークマン）

k+1桁目の数字の和はそれぞれ ( 0+2+3+4+5+6+7+8+9=44 ) ...44*10^k
また、0～9999までの数は、9進法の数と考えれば 9⁴個...
(ちなみに 10進法なら...10⁴ 個)
つまり、その桁以外の数は 9³個ということだから...
　　 44*9³*(10³+10²+10+1)/9⁴
　　=44*1111/9
　　(=5431.55556) ＞ 5000

解答・その9

（ペンネ－ム：ちょろんは太太）

０以上、１００００以下で、１を含まない整数は、一の位、十の位、百の位、千の位が、０、２，３，４，５，６，７，８，９　の９個の整数で作られるもの。
総数は、9⁴ 個である。次に、合計を求める。
特定の数 m （ 0, 2, 3, ・・・）について考える。
この数が、ある位にあらわれる回数は、それ以外の３つの位の数の組み合わせ 9³ 回である。
それぞれの位について考慮すれば、m が合計に寄与する分は、m×(1+10+100+1000)×9³
すべての m について考えると、合計は、(0+2+3+4+5+6+7+8+9)×(1+10+100+1000)×9³
よって、平均は、

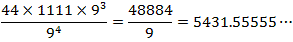
これで思ったのですが、
　　99までの和　45 x 110
　　999までの和　45 x 11100
　　9999までの和　45 x 1111000
　　99999までの和　45 x 111110000
　　999999までの和　45 x 11111100000
になるんですね、当たり前かと思いますが・・・

解答・その10

（ペンネ－ム：まめ）

平均なので、個数と総和をそれぞれ求めればよい。
尚、0～10000までとなっているが、10000は明らかに含まれないので、0～9999までの個数と総和を求める。

まずは個数から求める。
1が使えない、即ち0と2～9まで9種類の数字しか使えない世界。
よって9進数で表した0～8888までの数字の個数と同義。

0～8888までの個数は、9進数で表して10000個。
9進数の10000は10進数で 9⁴（＝6561）
従って、0～10000まで、1が現れない数字の個数は9⁴個。

次に総和。
まず1桁目では、0と2～9までの和が何セットあるかを考えればよい。
1を除く0～9までの和は、
　　(0＋9)×10÷2－1＝44
　　0～10まではこれが1セット、
　　0～100までは、9セットあるし、
　　0～1000となると9×9セットあるし、
　　0～10000となると9×9×9セットあるから、全部で
　　44×9³である。

このセットの数は2桁目、3桁目、4桁目でも同じ。
従って総和は
　　(44×10³＋44×10²＋44×10¹＋44×10⁰)×9³

よって、平均は
　　(44×10³＋44×10²＋44×10¹＋44×10⁰)×9³÷9⁴
　＝(44×10³＋44×10²＋44×10¹＋44×10⁰)÷9
　＝44÷9×1111

（答）9分の48884　または　5431と9分の5　あるいは　5431.5(・)　
　　　　(・)は小数第1位以降、5が循環することを表す
それにしてもこんな問題、小学生が解けるのでしょうか？

考察
たぶん、0～10ⁿまでの中でa,b,c・・・が現れない数字の総平均は、一般解として
　　S×(10⁰＋10¹＋10²＋・・・＋10^n-1)÷p
と書けるのかな。
　　S＝45－a－b－c－・・・，p＝10－現れない数字の数。
（例）0～100000まで、1、3、5、8が現れない数字の総平均は
　　S＝2＋4＋6＋7＋9＝28、
　p＝6ということで、
　　28×11111÷6＝51851.3(・)

解答・その11

（ペンネ－ム：迷子の雄猫）

まず10,000は1を含むので除外する。
残りの整数は4桁で表記できるので、先頭に0を補って4桁の固定長で表記する。
(つまり0001,0002,0003, .... ,0100,0101, .... , 9999)
さらにその中で1を含む数字を除外すると、各桁が0,2,3,4,5,6,7,8,9のいずれかで出来ている数字のみが残る。
残った数字は各桁が0,2,3,4,5,6,7,8,9のいずれも同じ頻度で（つまり同じ回数ずつ）出現する。
よって、1の位だけみるとその平均値は44/9になる。
10,100,1000の位も同様なので、平均は1111×(44/9)=48884/9

解答・その12

（ペンネ－ム：杖のおじさん）

答え　　４８８８４/９

各位で１が含まない数字の合計は
１の位（２＋９）×８÷２＝４４・・・(1)
１０の位（２＋９）×８÷２×１０＝４４０・・・(2)
１００の位（２＋９）×８÷２×１００＝４４００・・・(3)
１０００の位（２＋９）×８÷２×１０００＝４４０００・・・(4)
(1)＋(2)＋(3)＋(4)＝４８８８４になります。従って平均は次の通りです。
４８８８４/９となります。

解答・その13

（ペンネ－ム：転位反応）

０～１００００のうち、１を含まない整数は最大４桁であるから、それをＡＢＣＤとする。Ａ、Ｂ、Ｃ、Ｄは、それぞれ０、２、３、・・・、８、９の数なので、全ての組合せは９^４通りあり、９９９９、９９９８、・・・・、３、２　の総和を単純に加算して求めるのは容易ではない。
そこで、Ａ＝９の場合について具体的に考えてみると、４桁の整数は９ＡＢＣと表現でき、Ｂ、Ｃ、Ｄについての全ての組合せは９^３通りである。つまり、９９９９、９９９８、・・・　のように、９０００を含む数字が９^３個存在することになる。
同様にして、Ｂ＝９の場合、４桁の整数はＡ９ＣＤと表現でき、Ａ、Ｃ、Ｄについての全ての組合せは９３通りである。つまり、９００を含む数字も９^３個存在することになる。
よって、９９９９＝９０００＋９００＋９０＋９のように分解して加算すれば良い。
総和＝９０００×９^３＋９００×９^３＋９０×９^３＋９×９^３
　　　　＋８０００×９^３＋８００×９^３＋８０×９^３＋８×９^３
　　　　＋・・・・・・
　　　　＋２０００×９^３＋２００×９^３＋２０×９^３＋２×９^３
　　　＝（２＋３＋・・・＋９）×１０００×９^３＋（２＋３＋・・・＋９）×１００×９^３
　　　　＋（２＋３＋・・・＋９）×１０×９^３＋（２＋３＋・・・＋９）×９^３
　　　＝４４×１０００×９^３＋４４×１００×９^３＋４４×１０×９^３＋４４×９^３
　　　＝１１１１×４４×９^３
よって、平均値＝１１１１×４４×９^３／９^４
　　　　　　　　　＝１１１１×４４／９
　　　　　　　　　＝４８８８４／９

解答・その14

（ペンネ－ム：もげぴ）

４桁の整数００００～９９９９までについて考えます。
（設題は０から「１００００」までの整数についてですが，１００００は「１」が使用されているのでこの時点で除外します。また，「１」等の１桁の数は，便宜上「０００１」と表記するものとして検討します。）
４桁の整数○○○○のうち，１が現れないもの全てが対象なので，「０，２，３，４，５，６，７，８，９」の９つの整数を組み合わせてできる４桁の整数を考えます。このような整数の個数は，９×９×９×９＝６５６１個です。
次に，このような整数の全ての和を求めます。１の位には，０及び２から９までの９種類の数が，９×９×９＝７２９個ずつあるはずなので，１の位の数の合計は，
　　（０＋２＋３・・・＋８＋９）×７２９＝４４×７２９
となります。１０の位の数の合計，１００の位の数の合計，１０００の位の数の合計も，４４×７２９となります。したがって，このような４桁の整数の和は，
　　　４４×７２９＋１０×４４×７２９＋１００×４４×７２９＋１０００×４４×７２９
　　＝（１＋１０＋１００＋１０００）×４４×７２９
　　＝１１１１×４４×７２９
です。したがって平均を出すと，
　　　１１１１×４４×７２９／６５６１＝４８８８４／９＝となります。

解答・その15

（ペンネ－ム：SOU）

I) 10000はいらないので0～9999 までの数で1を含む数の総和を求める。
　(1) 1の個数が4つの時
　　1111 = 101x11 のみ
　(2) 1の個数が3つの時
　　111X,11X1,1X11,X111　　の4パターンがある。
　　各々のパターンにおいて、X の部分に入る値は0,2～9 の9通りある。
　　そこで1 の部分とX の部分を分けて考える。
　　ｲ) 1110,1101,1011,111 が各々9個
　　　　→ (1110+1101+1011+111)x9 = 3333x9 = 101x11x3³
　　ﾛ) (2+3+…+9)+(20+30+…+90)+(200+…+900)+(2000+…+9000) = 101x11²x2²
　(3) 1の個数が2つの時
　　ﾊ) 1が2つと0が2つの組み合わせ 1100,1010,…,111 の個数は0の入る場所が2箇所なので各々9x9個
　　　　→ (1100+1010+…+11)x9x9 = 3333x9x9 = 101x11x3⁵
　　ﾆ) ((2+3+…+9)x9+(20+30+…+90)x9+(200+…+900)x9+(2000+…+9000)x9)x3 = 101x11²x2²x3³
　(4) 1の個数が１つの時
　　ﾎ) 1111*9*9*9 = 101x11x3⁶
　　ﾍ) 1111*44*3*9*9 = 101x11²x2²x3⁵

II) 1を含まない数の和
　　ﾄ) 全体 = 0+1+2+…+9999 = 101x11x5⁴x3²x2³
　　ﾁ) 1を含む数の和 = 359x101x11x3²x2²
　　ﾘ) 1を含まない数の和 = ﾄ) - ﾁ) = 101x11x3²x2²(5⁴x2-359) = 101x11²x3⁶x2²

III) 1を含まない数の個数を求め、ﾘ) を割る
　I) の(1)～(4) と同じ分け方で考えると、1を含まない数の個数は
　　10000 - (1 + 9x4 + 9x9x6 + 9x9x9x4) = 3⁸

従って平均は
　　　101x(11x2/3)²

解答・その16

（ペンネ－ム：エルドス）

１０進ＢＡＳＩＣによる解答

CLEAR
FOR I= 0 TO 10000
   FOR K=0 TO 4
      IF MOD(INT(I/10^K),10)=1 THEN GOTO 100
   NEXT K
   LET S=S+I
   LET J=J+1
100 NEXT I
    PRINT "S=";S,"J=";J,"S/J=";S/J
 END

出力結果
１が現れないものの和S= 35636436　、個数J= 6561　、平均S/J= 5431.55555555556

解答・その17

（ペンネ－ム：三角定規）

各位の数が1ではない0以上10000未満の数の総和は

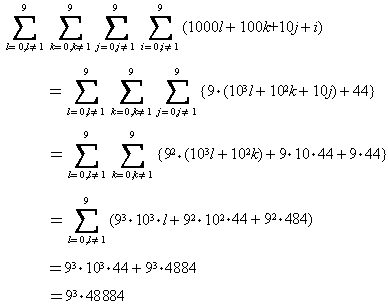
このような数は，各位の数がが0～9，≠1で9通り，計9⁴ 個あるから，平均は

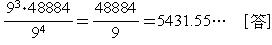
＜別解＞
題意を満たす数の各位には 0，2，～，9 が均等に現れるから，

数の平均＝各位の数の平均の（桁の重みをつけた）和

＝(44/9)×1111
＝48884/9
＝5431.55…　…［答］

解答・その18

（ペンネ－ム：オヤジ）

１を使用しないので｛０，2，３，４，５，６，７，８，９｝の９個の数字しか用いない。
従って　０～１００００の数字のうち、１を含まないのは　９^４＝６５６１個
０～１００００の数字のうち、１を含まない数の和は、
　　　４４×１１１１×７２９＝３５，６３６，４３６
よって求める平均は，
　　　４４×１１１１×９^３÷９^４＝４８８８４／９
　　　∴　４８８８４／９

解答・その19

（ペンネ－ム：Part Marty）

まず、１が現れない数字は各桁9個しか数字が使えないので、9*9*9*9個である。
１が現れない数字の合計は、
一の桁が0,2,3,4,5,6,7,8,9が個々に9*9*9個あるので0,2,3,4,5,6,7,8,9合計(2+9)*8/2*9*9*9=44*9*9*9
十の桁が0,2,3,4,5,6,7,8,9が個々に9*9*9個あるので00,20,30,40,50,60,70,80,90合計(2+9)*8/2*10*9*9*9=440*9*9*9
百の桁が0,2,3,4,5,6,7,8,9が個々に9*9*9個あるので合計(2+9)*8/2*100*9*9*9=4400*9*9*9
千の桁が0,2,3,4,5,6,7,8,9が個々に9*9*9個あるので合計(2+9)*8/2*1000*9*9*9=4400*9*9*9
よって合計は44*9*9*9*(1+10+100+1000)
従って平均は44*9*9*9*(1+10+100+1000)/(9*9*9*9)=1111*44/9=48884/9

下記の様にmaximaで確認しました。48884/9となりました。

kill(all);
nnn:0$nn:0$for a:0 thru 9 do
    for b:0 thru 9 do        
　　　for c:0 thru 9 do            
　　　　for d:0 thru 9 do                
　　　　　if a#1 or b#1 or c#1 or d#1 then 
 [nnn:nnn+a*1000+b*100+c*10+d,nn:nn+1]
$nn;nnn;nnn/nn;

どの桁にも「１が現れないようなもの」を考えるには、最初から「１」という数字がないと思えばいいのでしょうか。
残りの９個の数字は、偏ることなく対称性をもって出現します。
従って１桁目の平均が、
　　（０＋２＋３＋・・・＋９）/９＝４４/９
これがすべての桁で起こっていると考えればよいわけです。
　　（１０００＋１００＋１０＋１）（４４/９）＝４８８８４/９となります。
数の平均を考える時に、その数に注目するのではなく、桁ごとに考えるというアイディアですね。

Challenge!