Challenge!

問題178　最小公倍数の問題
Weekend Mathematics／問題／問題178　最小公倍数の問題

問題178　最小公倍数の問題

４つの相異なる１桁の正の整数がある。 これらの最小公倍数として考えられる最大の値を求めてください。

問題の出典

数学オリンピック
日本評論社
第18回日本数学オリンピック予選(2008年)

解答

～到着順にご紹介します～

解答・その1

（ペンネ－ム：スモークマン）

明らかではあるが...
互いに素な一桁の数を分類するとしたの４種類になるので...
　　2, 22=4, 23=8
　　3, 32=9
　　5
　　7

それぞれの組から最大数を選べばいい!!
つまり...
　　23*32*5*7=2520
のはず...

解答・その2

（ペンネ－ム：オヤジ）

最小公倍数（Ｌ．Ｃ．Ｍ）を、考えるとき、

  1. 互いに素な方が数の積の方が大きくなる。

  2. 大きな数の方が、積が大きくなる可能性がある。

  3. １桁の素数は、｛２，３，５，７｝である。

従って,　 １桁の最小公倍数で最大となるのは、９と８と７と５の積

∵　（Ⅰ）６は、９と８の最小公倍数７２の約数
　　（Ⅱ）９＝３２，　８＝２３　，７：素数　，５：素数　，４数は互いに素

従って　１桁の４数の正の整数の最小公倍数が最大となるのは，
　　∴　９×８×７×５＝２５２０

解答・その3

（ペンネ－ム：haya）

答： 2520

【解き方】
積が最大となる4つの相異なる１桁の正の整数の組合せは 9, 8, 7, 6 であるが、素因数分解すると、

　　

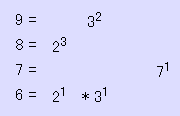
であることより、最小公倍数は単純な積とならず、
　　9 * 8 * 7 = 504
となる。　6 を次に大きな数 5 で代用すると、

　　

より、求める解、
　　9 * 8 * 7 * 5 = 2520
を得る。

*　 4数の最小公倍数を求めるサブルーチンを作って総当たりのチェックをしてから投稿しました。 堅固に作ったので2桁にも使える筈、ところが1桁は直ぐに答えが出るのに、2桁は沈黙が続いたのでびっくり。
　　89403930 = 99 * 98 * 97 * 95
と出て、1桁の場合同様「繰り上がり当選」でした。　 最小公倍数は急激に数字が大きくなるのでプログラムは3桁以上には使えないことが分かりましたので、
　　9・・・9, 9・・・8, 9・・・7, 9・・・6, 9・・・5
を直接素因数分解して眺めると、少なくとも5桁までは同じパターンですね。 9・・・6 から2と3の約数が出るので当然か。

解答・その4

（ペンネ－ム：浦岡）

９、８、７のどの２つも互いに素であることから、
９、８、７、６の最小公倍数（９・８・７＝５０４）と ９、８、７、５の最小公倍数（９・８・７・５＝２５２０）を吟味すれば十分である。
ゆえに、９・８・７・５＝*２５２０* …（答）

解答・その5

（ペンネ－ム：のっこん）

　　9＝32
　　8＝23
　　7＝71
　　6＝2・3
　　5＝51
　　　・・・

9、8を選べば6の因数としての2と3はそこに吸収されてしまう
よって最大の値は　5・7・8・9＝2520

解答・その6

（ペンネ－ム：転位反応）

題意を満たすには、お互いに素であって、かつ、 できるだけ大きな１桁の自然数を選べば良いので
９、８、７、５　の四つとなる。
よって、求める最小公倍数は、
　　９×８×７×５＝２５２０

解答・その7

（ペンネ－ム：atsuhiro）

まず最小公倍数の性質から
　　(４数の最小公倍数)≦(４数の積）・・・(1) は明らか.
次に４つの相異なる１桁の正の整数の積が最も大きくなる組み合わせは 6,7,8,9であるが、この組の最大公約数7*8*9
２番目に大きくなる組み合わせは5,7,8,9であり、 この組の最小公倍数は5*7*8*9 （ ＞7*8*9 ）
(1)より最小公倍数がこれを超える組み合わせは存在せず、これが最大である。

解答・その8

（ペンネ－ム：ちょろんは太太）

１から９までの正の整数すべてを素因数分解する。
1,2,3,22,5,2･3,7,23,32
これらすべての最小公倍数は、23･32･5･7
この中から４つの整数を選んでその最小公倍数を求めると、この値以下になる。
また、この値は、４つの整数（8, 9, 5, 7）の最小公倍数にもなっている。
従って、これは求める４つの１桁の整数の最小公倍数の最大値でもある。
答え：　23･32･5･7=2520

解答・その9

（ペンネ－ム：浜田　明巳）

一般的に，大きな数を沢山使えば，その最小公倍数は大きくなる．
　　１
　　２
　　３
　　４＝２２
　　５
　　６＝２×３
　　７
　　８＝２３
　　９＝３２
であるから，４数の中に８，９を入れれば，それらより２，３の素因数数が少ない２，３，４，６を入れる必要はない．
　故に４数は，５，７，８，９となり，それらの最小公倍数は
　　２３×３２×５×７＝２５２０
である．

　これを下記のエクセルのマクロでチェックしてみると，確かにそうなっている事を確認できる．

Option Explicit

Sub Macro1()

    Dim a As Integer

    Dim b As Integer

    Dim c As Integer

    Dim d As Integer

    Dim l As Integer

    Cells(1, 1).Value = 0

    Range("A1").Select

    For a = 1 To 9 - 3

      For b = a + 1 To 9 - 2

        For c = b + 1 To 9 - 1

          For d = c + 1 To 9

            l = LCM(LCM(a, b), LCM(c, d))

            If Cells(1, 1).Value < l Then

              Cells(1, 1).Value = l

              Cells(1, 2).Value = a

              Cells(1, 3).Value = b

              Cells(1, 4).Value = c

              Cells(1, 5).Value = d

            End If

          Next d

        Next c

      Next b

    Next a

End Sub

Private Function GCM(ByVal a As Integer, ByVal b As Integer) As Integer

    If b = 0 Then

      GCM = a

    Else

      GCM = GCM(b, a Mod b)

    End If

End Function

Private Function LCM(ByVal a As Integer, ByVal b As Integer) As Integer

    LCM = a * b / GCM(a, b)

End Function

解答・その10

（ペンネ－ム：夜ふかしのつらいおじさん）

各数を素因数分解すると、
　　1=1　2=2　3=3　4=22　6=2×3
　　5=5　7=7　8=23　9=32
最小公倍数を考えるので、大きい順にみます。
9、8、7までは互いに素なので問題なくリストされます。
次の6ですが、その因数の3も2も既に9と8がもっています。
6をリストしても最小公倍数は大きくなりません。
そこで、リストしてある3つの数と素である5を加えます。
最小公倍数は、9×8×7×5＝2520

解答・その11

（ペンネ－ム：Ryu1128）

4つの数の最小公倍数は4つの数の積を、共通の因数で割れば求まります。
4つの相異なる一桁の正の整数のうち、7,8,9は互いに素（注1）
これらに対し互いに素で最大の数は5（素数なので）です
6は、8と9に共通の因数2,3を持ちますので・・。
よって最大の最小公倍数は5＊7＊8＊9＝2520・・

因みに他の組み合わせをつくり小さいほうからｎ1、ｎ2、ｎ3、ｎ4
とした場合ｎ1≦5、ｎ2≦7、ｎ3≦8、ｎ4≦9となることからも明らかです。（左式の不等号の内少なくとも1つは等号を含まない)

注1；
　　7：素数
　　8＝23
　　9＝32
互いに共通因数を持たない

2桁の数を考えてみました
　　95＝5*19
　　97＝素数
　　98＝2＊7＊7
　　99＝3＊3＊11
上記4数は互いに素です。
96は、98と因数2が共通します
従って2桁の場合の最小公倍数の最大は
　　95＊97＊98＊99＝89,403,930

解答・その12

（ペンネ－ム：マシャ）

【解答】
5*7*8*9=2520

【過程】
1から9までの数字を指数表示して考えました.
すると, 素因数が2,3,5,7の4つしかないことに気づきました.
4つの相異なる正の整数を選ぶので, この素因数の指数が最大のものを 選べば良いと考えました.
その結果上記のような解答にたどり着きました.

解答・その13

（ペンネ－ム：迷子の雄猫）

2520。
4桁の異なる1桁の整数の積は、最大で6×7×8×9であるので、最大でも3024にしかならない。
しかしこの数字は6,7,8,9の最小公倍数ではないので、6より一つ小さい5に入れ替えた
　　5×7×8×9=2520=5×7×23×32
が最大。

解答・その14

（ペンネ－ム：T_Tatekawa）

a と b が互いに素の場合，最小公倍数は ab になる．
1桁の正の整数は，4つの素数（2, 3, 5, 7）を持つ．
これら4つの素数の積は，4つの素数の最小公倍数．
ところで，1つの素数からなる1桁の合成数は
　　8=2*2*2
　　9=3*3
である．2, 3の代わりに8, 9を選ぶ．つまり
(5, 7, 8, 9) の4つの数の組み合わせを考えても，
これらは互いに素であるので，最小公倍数はこれらの積になる．
　　5*7*8*9 = 2520
が1桁の正の整数の最小公倍数として得られる最大値である．
なお，2520は1桁の正の整数全ての最小公倍数でもある．

解答・その15

（ペンネ－ム：ＡＮＤ）

9 8 7 6 5 4 3 2を素因数分解したら、以下の通りとなる。
　　32, 23, 7, 2*3, 5, 22, 3, 2
最小公倍数を構成する４つの数を考えると以下のようになり、
　　９，８，７，６ --> 23 * 33 * 7
　　９，８，７，５ --> 23 * 33 * 5 * 7
　　９，８，７，５の組合せが最大の最小公倍数となる

解答・その16

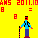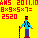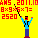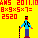（ペンネ－ム：杖のおじさん）

答え　最大値は２５２０です。
１桁の正の整数は１０以上の素数を持ちません
１，２，３，４，５，６，７，８，９、の中で１桁の因数分解した時、重複する物を除きました。
　　１→１
　　２→２×１
　　３→３×１
　　４→２×２
　　５→５×１
　　６→２×３×１
　　７→７×１
　　８→２×２×２
　　９→３×３
上記により２と３と５と７の指数を取り、それぞれの１桁が１０以上の素数を持たないようにするには次のようになります。
結果は２３×３２×５１×７１＝８×９×５×７＝２５２０です。
従って最大値は２５２０です。

解答・その17

（ペンネ－ム：三角定規）

2，3，4(=22)，5，6(=2・3)，7，8(=23)，9(=32) の中から選んだ 4 つの数の最小公倍数は，
４数の積が大きいほど，また，4 数の素因数の重複が少ないほど大きくなる。
よって，最小公倍数が最大となるのは，5，7，8(=23)，9(=32) を選んだときの 5・7・8・9＝2,520 …[答]

解答・その18

（ペンネ－ム：G3）

9×8×7×５=2520
単純に互いに素である数を大きいほうから4つとると９，８，７，５なので。

コメント

単純に大きい方から４つとればよいと考えてしまいがちですが、そうはなりません。
１桁の正の整数１つなら、もちろん９
１桁の正の整数２つなら、９と８、両者の最小公倍数は９×８＝７２です。
１桁の正の整数３つなら、９と８と７、これらの最小公倍数は、９×８×７＝５０４です。
ところが、１桁の正の整数４つの場合、９と８と７と６　というわけにはいきません。
９と８と７と６の最小公倍数は、やはり、９×８×７＝５０４です。
つまり、最小公倍数を大きくするために、６は貢献できていません。
それは、５０４＝３2×２3×７と素因数分解をしてみればわかります。
６＝２×３　ですから、６の持っている素因数は既に存在しています。

イノベーションを起こして、大きくなるためには、異質なものが必要ということでしょうか？

因みに、T_Tatekawaさんの解答にあるように、これ以上１桁の正の整数の数を増やしても、 素因数の数が増えないので、最小公倍数を大きくすることはできません。

また、hayaさん、Ryu1128さんが、 ２桁の正の整数についても言及してくださいました。

top