栤戣177丂巟暐偄偺栤戣
侾墌嬍丄10墌嬍丄100墌嬍丄1,000墌嶥傪崌傢偣偰60枃巊偭偰丄 偪傚偆偳丂10,000墌傪巟暐偆偙偲偑偱偒傞偱偟傚偆偐丅
栤戣偺弌揟
僷僘儖婥暘偱嶼悢僆儕儞僺僢僋
搶戝嶼悢尋媶夛丂曇廤
戞俀夞嶼悢僆儕儞僺僢僋丂寛彑栤戣
夝摎
乣摓拝弴偵偛徯夘偟傑偡乣
夝摎丒偦偺1
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
壜擻偩偲偡傞偲...
丂丂1000*a+100*b*10*c+d=10000
丂丂a+b+c+d=60
偑摨帪偵惉傝棫偮偼偢...but...
丂丂d=60-(a+b+c)
丂丂999*a+99*b+9*c=9940
嵍曈偼9偺攞悢
塃曈偼9偺攞悢偱側偄
偙傟偼柕弬偡傞偺偱...晄壜擻 ^^
夝摎丒偦偺2
乮儁儞僱亅儉丗塝壀乯
1墌,10墌,100墌,1000墌傪偦傟偧傟a枃,b枃,c枃,d枃(a,b,c,d伕帺慠悢)傪巊偆偲壖掕偡傞偲
戣堄傛傝丄師幃偑惉傝棫偮丅
丂丂a + 10b + 100c + 1000d = 10000 乧(1)
丂丂a + b + c + d = 60 乧(2)
(1)傛傝
丂丂(a + b + c + d) + 9(b + 11c + 111d) = 10000
丂丂60 + 9(b + 11c + 111d) = 10000 (佹(2))
丂丂9(b + 11c + 111d) = 9940
丂丂b + 11c + 111d = 9940/9 乧(仸)
偙偙偱丄(仸)偵偍偄偰
嵍曈偼帺慠悢偱偁傞偑丄塃曈偼帺慠悢偱偼側偄丅
亪戣堄偺傛偆側巟暐偄曽偼晄壜擻偱偁傞丅
夝摎丒偦偺3
乮儁儞僱亅儉丗偪傚傠傫偼懢懢乯
侾墌嬍丂i屄丄侾侽墌嬍丂j屄丄侾侽侽墌嬍丂k屄丄侾侽侽侽墌嶥丂m枃傪巊偭偨偲偡傞丅憤妟丂S 偼丄
丂丂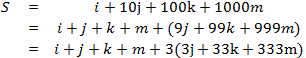
忦審偐傜丂i+j+k+m=60偩偐傜丄S 偼 昁偢3 偺攞悢偱偁傞丅
10000偼丄俁偺攞悢偱偼側偄偺偱丄偪傚偆偳60枃傪巊偭偰丄10000墌偵偡傞偙偲偼偱偒側偄丅
夝摎丒偦偺4
乮儁儞僱亅儉丗偺偭偙傫乯
1墌嬍傪a枃丄侾侽墌嬍傪b枃丄侾侽侽墌嬍傪c枃丄侾侽侽侽墌嶥傪d枃巊偭偰
乮 a,b,c,d 偼偄偢傟傕侽埲忋俇侽埲壓偺惍悢乯
偪傚偆偳侾侽侽侽侽墌傪巟暐偆偙偲偑偱偒傞傕偺偲偡傞偲
師偺(1)丄(2)偑惉傝棫偮
丂丂a+b+c+d=60 丒丒丒丒丒(1)
丂丂a+10b+100c+1000d=10000丂丒丒丒丒丒(2)
(2)亅(1)傛傝
丂丂9倐亄99們亄999倓亖9940丂丒丒丒丒丒(3)
(3)偺嵍曈偼俋偺攞悢偱偁傞偑丄塃曈偼俋偺攞悢偱側偄
偙傟偼柕弬偱偁傞
偙偺柕弬偼乽偪傚偆偳10000墌傪巟暐偆偙偲偑偱偒傞傕偺偲偟偨乿偙偲偵婲場偡傞
傛偭偰丄偪傚偆偳10000墌傪巟暐偆偙偲偼偱偒側偄
夝摎丒偦偺5
乮儁儞僱亅儉丗昹揷丂柧枻乯
侾墌嬍丆侾侽墌嬍丆侾侽侽墌嬍丆侾侽侽侽墌嶥偺屄悢丆嶥悢傪偦傟偧傟倎丆倐丆們丆倓偲偡傞偲丆忦審偐傜丆
丂丂倎亄倐亄們亄倓亖俇侽乧乧乧(1)
丂丂倎亄侾侽倐亄侾侽侽們亄侾侽侽侽倓亖侾侽侽侽侽乧乧乧(2)
(2)亅(1)偐傜丆
丂丂俋倐亄俋俋們亄俋俋俋倓亖俋俋係侽
丂丂亪俋(倐亄侾侾們亄侾侾侾倓)亖俋亊侾侾侽係亄係
嵍曈偼俋偺攞悢偱偁傝丆塃曈偼俋偺攞悢偱側偄偺偱丆柕弬偡傞丏
屘偵忦審傪枮偨偡惍悢倎乣倓偼懚嵼偟側偄丏
屘偵偪傚偆偳侾侽侽侽侽墌傪巟暐偆偙偲偼偱偒側偄丏
偲傝偁偊偢偙偺傛偆偵夝偄偨偑丆偙傟偼巹偵婜懸偝傟偰偄傞夝摎偱偼側偄偩傠偆丏偄偮傕偺傛偆偵丆僄僋僙儖偺儅僋儘偱夝偄偰傒傞丏
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Range("A1").Select
Dim x1 As Integer
Dim x10 As Integer
Dim x100 As Integer
Dim x1000 As Integer
For x1000 = 0 To Application.Min(Int(10000 / 1000), 60)
For x100 = 0 To Application.Min(Int((10000 - 1000 * x1000) / 100), 60 - x1000)
For x10 = 0 To Application.Min(Int((10000 - 1000 * x1000 - 100 * x100) / 10), 60 - x1000 - x100)
x1 = 60 - x1000 - x100 - x10
If 0 <= x1 And x1 <= 60 And 1000 * x1000 + 100 * x100 + 10 * x10 + 1 * x1 = 10000 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = x1
Cells(Cells(1, 1).Value, 3).Value = x10
Cells(Cells(1, 1).Value, 4).Value = x100
Cells(Cells(1, 1).Value, 5).Value = x1000
End If
Next x10
Next x100
Next x1000
End Sub
偙偺儅僋儘偵傛傝丆夝偼昞帵偝傟側偐偭偨偺偱丆傗偼傝巟暐偆偙偲偼偱偒側偄偲偄偆寢榑偵払偡傞丏
夝摎丒偦偺6
乮儁儞僱亅儉丗Part Marty乯
摎偊丗10,000墌傪巟暐偆偙偲偑偱偒側偄
侾墌嬍 a屄丄10墌嬍 b屄丄100墌嬍 c屄丄1,000墌嶥 d枃偲偡傞偲
a+10*b+100*c+1000*d=10000
a+b+c+d=60
a,b偵偮偄偰夝偔偲丄偄偐側傞惓偺惍悢c,d傪偲偭偰傕丄a,b偼惍悢偵側傜側偄丅
a=110*d+10*c-9400/9,b=-111*d-11*c+9940/9
a,c偵偮偄偰夝偄偰傕丄摨條
a=(100*d)/11-(10*b)/11-4000/99,c=-(111*d)/11-b/11+9940/99
a,d偵偮偄偰夝偄偰傕丄摨條
a=-(100*c)/111-(110*b)/111+50000/999,d=-(11*c)/111-b/111+9940/999
b,c偵偮偄偰夝偄偰傕丄摨條
b=10*d-(11*a)/10-400/9,c=-11*d+a/10+940/9
b,d偵偮偄偰夝偄偰傕丄摨條
b=-(10*c)/11-(111*a)/110+5000/99,d=-c/11+a/110+940/99
c,d偵偮偄偰夝偄偰傕丄摨條
c=-(11*b)/10-(111*a)/100+500/9,d=b/10+(11*a)/100+40/9
夝摎丒偦偺7
乮儁儞僱亅儉丗you乯
10,000墌傪崌寁枃悢偑掅偄弴偺昞傪埲壓偵嶌惉偡傞丅
| 丂 | 1 | 10 | 100 | 1000 | 寁 |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 10 | 10 |
| 2 | 0 | 0 | 10 | 9 | 19 |
| 3 | 0 | 10 | 9 | 9 | 28 |
| 丒丒丒 | 丂 | 丂 | 丂 | 丂 |
忋婰偺昞偺捠傝9偺攞悢+1枃偺僐僀儞偑昁梫偲側傞丅
偟偨偑偭偰丄60枃偱10,000墌偵偡傞偙偲偼丄9偺攞悢+1枃偱60枃偼 妱傝愗傟側偄偨傔偱偒側偄丅
夝摎丒偦偺8
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂侾侽侽侽侽墌傪巟暐偆偙偲偼弌棃傑偣傫
帋偟偵師偺曽朄傪偟偰傒傑偟偨丅
壓堦寘偑侽側偺偱侾墌偼嵟掅侾侽墌傪侾侽枃巊偆帠偵側傝傑偡丅
師偵侾侽墌傪巊偄擇寘栚傪侽偵偡傞偵偼俋枃巊偆帠偵側傝傑偡丅
師偵侾侽侽墌傪巊偄嶰寘栚傪侽偵偡傞偵偼俋枃傪巊偆帠偵側傝傑偡丅
偙偙偱傑偱偱俀俉枃侾侽侽侽墌偵側傝傑偡丅俁侽枃偵偡傞偨傔侾侽侽侽墌傪俀枃巊傑偡丅
崌寁偼俁侽枃俁侽侽侽墌偵側傝傑偡丅
俇侽枃偼俇侽侽侽墌偵側傝傑偡丅
偙偙偱巊偭偰偄傞庬椶偼師偺捠傝偱偡丅
侾墌仺俀侽枃丂侾侽墌仺侾俉枃丂侾侽侽墌仺侾俉枃丂侾侽侽侽墌仺係侽侽侽墌
俇侽枃巊梡偟偰崌寁俇侽侽侽墌偲側傝傑偡丅
偙偙偱晄懌妟偼侾侽侽侽侽墌乗俇侽侽侽墌亖係侽侽侽墌偱偡偺偱
巊梡偟偨俇侽枃悢傪曄偊側偄偱椉懼偟偰係侽侽侽墌偵憹傗偡偙偲偑弌棃傞偐峫偊偰傒傑偡丅
侾墌偐傜侾侽侽墌傑偱偺嬥妟傪忋埵偺嬥妟偵椉懼偡傞偲俋偲偄偆悢帤偑
侾侽侽埵丄侾侽埵丄侾埵偵弌偰偒傑偡偺偱俇侽枃偱侾侽侽侽侽墌偼巟暐偊側偄帠偵側傝傑偡丅
夝摎丒偦偺9
乮儁儞僱亅儉丗揮埵斀墳乯
亂夝朄侾亃戙悢曽掱幃傪巊偆曽朄
侾墌丄侾侽墌丄侾侽侽墌媦傃侾侽侽侽墌偺巊梡枃悢傪偦傟偧傟丄倎丄倐丄們丄倓偲偡傞偲丄
丂乮倎丄倐丄們丄倓偼丄偦傟偧傟侾埲忋偺惍悢乯
戣堄傛傝丄埲壓偺幃(1)丄(2)偑惉傝棫偮丅
丂丂倎亄倐亄們亄倓亖俇侽 丒丒丒(1)
丂丂倎亄10倐亄100們亄1000倓亖10000丂 丒丒丒(2)
幃(1)傛傝丄
丂丂倎亖俇侽亅倐亅們亅倓
幃(2)偵戙擖偟偰惍棟偡傞偲丄
丂丂俋倐+俋俋們+俋俋俋倓亖俋俋係侽
丂丂俋乮倐+侾侾們+侾侾侾倓乯亖俀亊俀亊俆亊俈亊俈侾丂丒丒丒(3)
幃(3)偺嵍曈偼栺悢偲偟偰俋傪娷傓偑丄塃曈偵偼娷傑側偄丅
亪幃(1)(2)傪摨帪偵枮偨偡惍悢倎丄倐丄們丄倓偼懚嵼偟側偄
亪戣堄傪枮偨偡巟暐偄曽朄偼晄壜擻偱偁傞
亂夝朄俀亃戙悢曽掱幃傪巊傢側偄曽朄
侾侽侽侽侽墌傪侾侽侽侽墌偲俋侽侽侽墌偵暘偗偰丄侾侽侽侽墌偼侾墌丄侾侽墌媦傃侾侽侽墌偺慻崌偣偱丄
俋侽侽侽墌偼侾侽侽侽墌傪俋枃偱巟暐偆偲偒丄峝壿媦傃巻暭偺巊梡枃悢傪嵟彮偵偟傛偆偲偡傞偲
壓昞偺働乕僗俙偲側傞丅
摨條偵偟偰働乕僗俛乣俢偵偮偄偰媮傔傞偲丄働乕僗俢偼梌審偺枃悢偱偁傞俇侽傪挻偊傞偙偲偑暘偐傞偺偱丄
埲屻丄働乕僗俙乣俠偵偮偄偰偺傒専摙偡傟偽椙偄丅
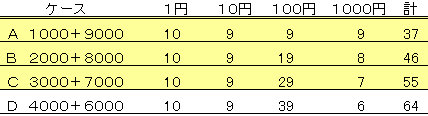
侾乯働乕僗俠偵偮偄偰丄巊梡枃悢偑師偵懡偄慻崌偣偼侾侽侽墌偺巊梡枃悢傪 侾枃尭傜偟偰丄
侾侽墌偺巊梡枃悢傪侾侽枃憹傗偡応崌偱偁傞丅丂
寢壥丄梌審偺枃悢俇侽傪挻偊偰偟傑偆偨傔丄働乕僗俠偺壜擻惈偼柍偄丅

俀乯働乕僗俛偵偮偄偰傕摨條偵丄巊梡枃悢偑師偵懡偄慻崌偣傪弴師媮傔偰惍棟偡傞偲
壓昞偺捠傝偱偁傞丅傛傝崅妟偺峝壿傪侾枃尭傜偟偰丄掅妟偺峝壿侾侽枃憹傗偡偺偱丄
崌寁偱偼俋枃憹偊傞偙偲偵側傞丅
寢壥丄梌審偺枃悢俇侽偵偼側傜側偄偨傔丄働乕僗俛偺壜擻惈偼柍偄丅
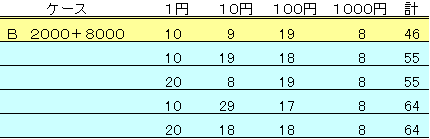
俁乯働乕僗俙偵偮偄偰傕摨條丄俋枃偢偮憹偊偰偄偭偰俇侽偵偼側傜側偄偺偱丄働乕僗俙偺壜擻惈傕柍偄丅
昞偵偼丄侾侽侽墌偺枃悢傪尭傜偟偰侾侽墌偺枃悢傪憹傗偟偨応崌傪帵偟偨丅
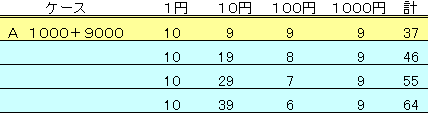
亪戣堄傪枮偨偡働乕僗偼柍偔丄巜掕偺巟暐偄曽朄偼晄壜擻偱偁傞丅
夝摎丒偦偺10
乮儁儞僱亅儉丗柪巕偺梇擫乯
晄壜擻丅
1,000墌嶥傪10枃巊偭偰丄偪傚偆偳丂10,000墌傪巟暐偆偙偲偑偱偒傞丅
偝偰偙偙偱丄1,000墌嶥傪100墌嬍偵丄100墌嬍傪10墌嬍偵丄10墌嬍傪侾墌嬍偵丄
偦傟偧傟椉懼偟偨偲偡傞丅
偳偺曽朄偱椉懼偟偰傕丄嶥乛峝壿偺枃悢偺崌寁偑9枃憹偊傞偺偱丄
10枃丄19枃丄28枃丄37枃丄46枃丄55枃丄64枃乮埲壓棯乯偱偟偐
偪傚偆偳丂10,000墌傪巟暐偆偙偲偑偱偒側偄丅
傛偭偰丄60枃巊偭偰丄偪傚偆偳丂10,000墌傪巟暐偆偙偲偼偱偒側偄丅
夝摎丒偦偺11
乮儁儞僱亅儉丗偗傫偨傫乯
摎偊丂偱偒傑偣傫丅
偪傚偆偳10,000墌巟暐偆偙偲偑偱偒傞偲偟偰丄1墌嬍丄10墌嬍丄100墌嬍丄1,000墌嶥偺枃悢傪偦傟偧傟
倎丄倐丄們丄倓偲偍偔偲
丂丂倎丄倐丄們丄倓偼慡偰惍悢
丂丂倎+倐+們+倓亖俇侽丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒(1)
丂丂倎+侾侽倐+侾侽侽們亄侾侽侽侽倓亖侾侽侽侽侽丒丒(2)
(2)亅(1)
丂丂俋倐+俋俋們+俋俋俋倓亖俋俋係侽
丂丂俋乮倐+侾侾們+侾侾侾倓乯亖俋俋係侽丒丒丒(3)
偙偙偱丄倐丄們丄倓偼惍悢偱偁傞偐傜丄倐+侾侾們侾侾侾倓傕惍悢丅丒丒丒(4)
偟偐偟丄(3)傛傝
丂丂倐+侾侾們侾侾侾倓亖俋俋係侽乛俋
偲側傝丄丂丂惍悢偲側傜側偄丅丂丂丂丂丂丂丂丂丂丂丂丒丒丒(5)
傛偭偰丄(4) (5)偑柕弬偡傞偨傔巟暐偆偙偲偑偱偒側偄丅
夝摎丒偦偺12
乮儁儞僱亅儉丗僄儖僪僗乯
俠尵岅偱慻傫偱傒傑偟偨丅60枃偱偼侾侽侽侽侽墌偵側傞偙偲偼側偄偱偡偹丅
#includemain() { int i,j,k,l,m; for (i=0;i<=60;i++){ for (j=0;j<=60;j++){ for (k=0;k<=60;k++){ l=60-(i+j+k); if (l<0) {continue;} m=i+10*j+100*k+l*1000; if (m==10000) {printf("%d%d%d%d%d",m,i,j,k,l);} } } } return 0; }
夝摎丒偦偺13
乮儁儞僱亅儉丗haya乯
摎丗 晄壜擻
亂夝偒曽亃
亸1000嶥傪4枃傑偱尭傜偡偲丄嵟戝嬥妟偱傕丄
丂丂54*100 + 1*10 + 1*1 = 9411 亙 10000
偲丄嬥妟晄懌偲側傞丅丂媡偵亸1000嶥傪10枃揔梡偡傟偽嬥妟挻夁偲側傞偙偲偐傜丄
丂丂4 亙 亸1000嶥偺枃悢 亙 10
偱偁傞丅丂偦傟偧傟偺応崌偵偮偄偰崌寁嬥妟偑亸10000偵愙嬤偡傞慻崌偣傪挷嵏偡傞偲丄
壓偺Fig.1偺擛偔丄11屄偺応崌偑偁傞偑壗傟傕挌搙亸10000偲偼側傜偢丄
崌寁嬥妟乮Sum楍乯偑亸10000傪屪偄偱偟傑偆偺偱乽晄壜擻乿偑摎偊偲側傞丅
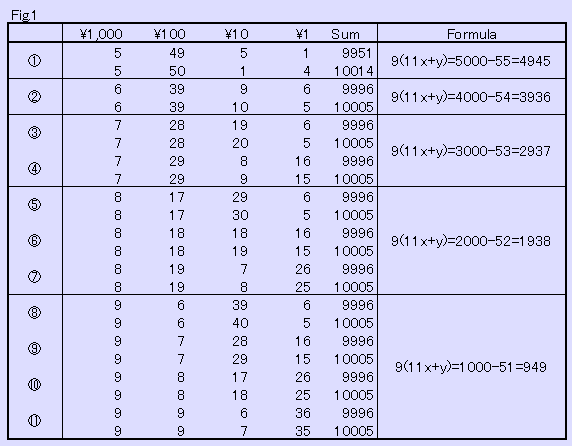
偙偺偙偲偼丄9偺攞悢偲側傜側偄偙偲偐傜傕愢柧偱偒傞丅
椺偊偽丄嘆偱偼亸1000嶥傪5枃巊偭偰偄傞偐傜丄巆傝偺亸100, 亸10, 亸1 傪偦傟偧傟
x, y, z 偲偟偰
丂丂
嵍曈偼9偺攞悢偱偁傞偑塃曈偼9偺攞悢偱偼側偄偺偱丄x, y 偵惍悢夝偼側偄
乮懠偺応崌偵偮偄偰偼Formula楍偺摉奩幃嶲徠乯丅
夝摎丒偦偺14
乮儁儞僱亅儉丗傕偘傄乯
枃悢偼偝偰偍偒丆崌寁嬥妟偑侾侽丆侽侽侽墌偱偁傞忬懺偱丆偁傞嬥庬偺枃悢傪曄偊傞偵偼丆
椺偊偽侾侽侽侽墌嶥傪侾枃尭偠偨傜侾侽侽墌嬍傪侾侽枃憹傗偡昁梫
偑偁傝乮亖憤枃悢俋枃憹壛乯丆
媡偵侾侽侽墌嬍傪侾枃憹傗偡側傜侾侽墌嬍傪侾侽枃尭傜偡偙偲偵側傞乮亖憤枃悢俋枃尭彮乯丅
偮傑傝丆偁傞嬥庬傪侾枃尭偠偨 乮傑偨偼憹傗偟偨乯応崌丆
偦偺侾侽暘偺侾偺嬥庬傪侾侽枃憹傗偡乮傑偨偼尭偢傞乯昁梫偑偁傞乮偙偺嶌嬈傪乽椉懼乿偲尵偆偙偲偵偡傞丅乯丅
椺偊偽丆侾丆侽侽侽墌嶥侾侽枃偺忬懺乮崌寁侾侽丆侽侽侽墌乯傪僗僞乕僩偵擟堄偺夞悢椉懼傪懕偗傞偙偲偱丆
崌寁妟偑侾侽丆侽侽侽枩墌偵側傞嬥庬偲枃悢偺偁
傜備傞慻傒崌傢偣偑嶌傟傞偑丆椉懼偺偨傃憤枃悢偼俋枃偢偮憹尭偡傞偨傔丆偳傟偩偗椉懼傪懕偗偰傕丆憤枃悢偑俇侽枃偵側傞偙偲偼側偄丅
夝摎丒偦偺15
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
仠1墌嬍傪 x 枃丄10墌嬍傪 y 枃丄100墌嬍傪 z 枃丄1000墌嶥傪 w 枃偲偟傑偡丅
戣堄偐傜丄丂
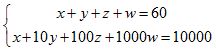
忋偺曽掱幃偐傜 丄x = 60 - y -z -w 丄 偙傟傪壓偺曽掱幃偵戙擖偡傞偲丄
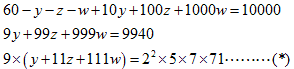
偲側傝傑偡丅
偙偺曽掱幃偺嵍曈偼9偺攞悢偱偡偑丄塃曈偼偦偆偱偼偁傝傑偣傫丅
偼惍悢側偺偱丄(*)偺曽掱幃偼夝偑偁傝傑偣傫丅
偮傑傝丄1墌嬍丄10墌嬍丄100墌嬍丄1000墌嶥偺崌寁偑60枃偱10000墌偼巟暐偊傑偣傫丅
仠(10000亅枃悢)偑9偺攞悢偱偁傞偙偲偑昁梫偱偡丅
椺偊偽64枃側傜偽丄
丂丂9亊(y + 11z + 111w) = 10000 - 64 = 9936 = 9亊1104
丂
側偺偱丄
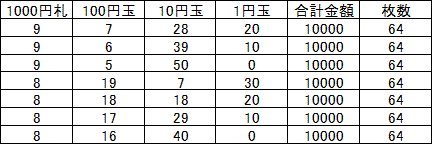
偺傛偆偵巟暐偄偑壜擻偱偡丅
夝摎丒偦偺16
乮儁儞僱亅儉丗Ryu1128乯
侾墌嬍偐傜愮墌嶥偺奺枃悢傪値1丄値2丄値3丄値4偲偟
崌寁傪俶偲偟傑偡 乮値i偼0偐惓偺惍悢偱偡)
偙偙偱偼俶亖60
偝傜偵丄崌寁嬥妟傪俽偲偟俽偼侽偱偼側偄惓偺10000墌偺攞悢偲偟傑偡
戣堄偐傜丄師偺幃偑惉傝棫偪傑偡
丂丂丂値1+10 値2+100 値3+1000 値4亖俽丂丂丂偙偙偱偼俽亖10000
丂丂丂値1+値2+値3+値4亖俶丂丂丂偙偙偱偼俶亖60
偙偙偱師偺傛偆偵偍偒傑偡乮倣i偼0偐惓偺惍悢*1偱偡)
丂丂丂倣1亖値1/10
丂丂丂倣2亖乮値1+10 値2乯/100
丂丂丂倣3亖乮値1+10 値2+100 値3乯/1000
丂丂丂倣4亖乮値1+10 値2+100 値3+1000 値4乯/10000丂丂
丟倣4亖俽/10000
丂丂丂丂丂丂偙偙偱偼倣4亖1
忋婰偐傜壓婰幃偑摫偐傟傑偡
丂丂丂侾侽倣1亖値1
丂丂丂侾侽倣2亖倣1+値2
丂丂丂侾侽倣3亖倣2+値3
丂丂丂侾侽倣4亖倣3+値4
忋婰曈乆懌偡偲丄
丂丂丂10乮倣1亄倣2亄倣3亄倣4乯
亖乮倣1+倣2+倣3乯
+乮値1+値2+値3+値4乯
丂丂丂10乮倣1亄倣2亄倣3乯亄10倣4
亖乮倣1+倣2+倣3乯+俶
丂丂丂倣1亄倣2亄倣3亖倠偲偍偔偲乮倠偼0偐惓偺惍悢乧(1)乯
丂丂丂倠亖乮俶-10倣4乯/9丒丒丒丒丒倠偺偲傝偆傞抣偺昁梫忦審
戣堄偵増偭偰俶偲倣4傪戙擖偡傞偲
丂丂丂倠亖乮60-10乯/9亖50/9乧(2)
(2)偼(1)偵斀偡傞偺偱晄壜擻丒丒丒丒丒夞摎
*1 倣i偑侽偐惓偺惍悢偱柍偗傟偽側傜側偄偺偼奺寘偑孞傝忋偑偭偰
嵟廔揑偵崌寁偑S偵側傜側偗傟偽側傜側偄帠偐傜帺柧丅
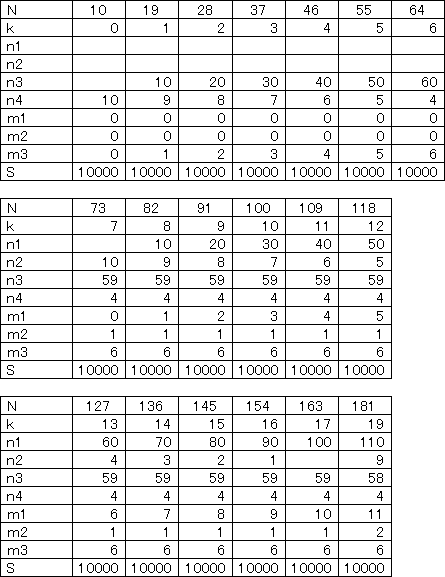
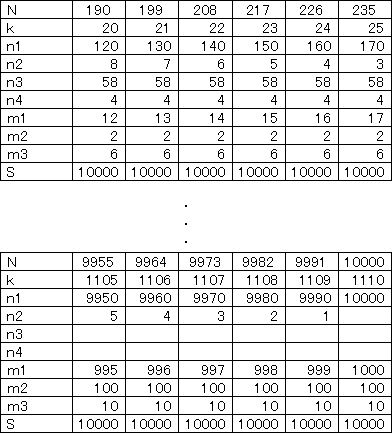
場傒偵倣4=侾偲偟偨帪偺N偱壜擻側応崌偼
丂丂丂N=10丄19丄28丄37丄46丄55丄64丒丒丒丒丄10000
偱丄N-10偑俋偱妱傝愗傟妿偮N亝S丒丒丒丒昁梫廩暘忦審
壓婰昞偱傕妋偐傔傑偟偨偑丄S偺抣偱俶偑掕傑傝丄
倠抣偵傛傝値i偑堦堄偵寛傑傞偲偄偆偺偼彮偟姶摦揑偱偟偨丅
夝摎丒偦偺17
乮儁儞僱亅儉丗俙俶俢乯
夝摎丗丂暐偊傑偣傫丅
壖偵丄1000墌嶥傪a枃丄100墌嬍傪倐枃丄10墌嬍傪們枃丄1墌嬍傪倓枃巊偆偲偡傞偲丄
忋婰傪枮偨偡偵偼丄埲壓偺2幃傪摨帪偵枮偨偡丄侽埲忋偺惍悢a,b,c,d偺慻崌偣偑
懚嵼偡傞昁梫偑偁傝傑偡丅
丂丂丂幃1) 1000a + 100b + 10c + d = 10000
丂丂丂幃2) a + b + c + d = 60
偙偙偱幃侾偐傜幃俀乯傪堷偔偲丄埲壓偺捠傝偲側傝傑偡丅
丂丂丂幃3) 999a + 99b + 9 c = 9940
偙偙偱嵍曈傪俋偱妵傝丄塃曈傪慺悢暘夝偡傞偲埲壓偺傛偆偵側傝傑偡丅
丂丂丂幃3)乫丂9*(111a + 11b + c) = 22 * 5 * 7 * 71
幃3)乫偺嵍曈偼俋偺攞悢偲側傝傑偡偑丄塃曈偼9偺攞悢偱偼偁傝傑偣傫丅
廬偭偰丄幃俁乯乫傪枮偨偡 a,b,c,d偺0埲忋偺惍悢偺慻崌偣偼懚嵼偟傑偣傫丅
屘偵丄侾墌嬍丄10墌嬍丄100墌嬍丄1,000墌嶥傪崌傢偣偰60枃巊偭偰丄偪傚偆偳丂 10,000墌傪巟暐偆偙偲偼丄偱偒側偄偲尵偊傑偡丅
夝摎丒偦偺18
乮儁儞僱亅儉丗僆儎僕乯
侾墌嬍X枃丄侾侽墌嬍Y枃丄侾侽侽墌嬍Z枃丄侾侽侽侽墌嶥W枃丄偱侾枩墌傪巟暐偍偆偲偡傞偲丅
丂丂X+侾侽Y亄侾侽侽Z亄侾丆侽侽侽W亖侾侽丆侽侽侽丂丒丒丒乮侾乯
乮侾乯傪枮偨偡巟暐偄曽朄偼丄柍悢偵偁偭偰丄椺偊偽
乷乮X丆Y丆Z丆W乯乥乮侽丆侽丆侽丆侾侽乯丆乮侽丆侽丆侾侽丆俋乯丆乮侽丆侾侽丆俋丆俋乯丆
乮侾侽丆俋丆俋丆俋乯丆乮俁侽丆侾俈丆侾俉丆俉乯丆倕倲們丒丒乸
侾侽墌嬍乣侾侽侽侽墌嶥傑偱偳傟傪侾枃乮偁傞偄偼丄侾屄乯尭傜偡偲嬥妟偑摨偠偱偁傟偽
堦寘壓偺埵偺侾墌嬍乣侾侽侽墌嬍偑侾侽屄憹偊傞偺偱丄俋偺攞悢屄憹偊傞帠偵側傞丆
俶傪丆侽埲忋偺惍悢偲偡傞偲丄侾侽丆侽侽侽墌巟暐偆偵偼丄
丂丂X+Y亄Z亄W亖侾侽亄俋俶丂丒丒丒丒乮俀乯
丂丂侾侽亄俋俶亖俇侽丂丒丒丒乮俀乯
傪枮偨偡侽埲忋偺惍悢偼丄懚嵼偟側偄丅
亪侾墌嬍丄侾侽墌嬍丄侾侽侽墌嬍丄侾侽侽侽墌傪崌傢偣偰俇侽枃巊偭偰丄 侾侽丆侽侽侽墌傪巟暐偆偙偲偼丄弌棃側偄丅丂
夝摎丒偦偺19
乮儁儞僱亅儉丗atsuhiro乯
1墌嬍丆侾侽墌嬍丆100墌嬍丆1000墌嶥傪偦傟偧傟x,y,z,w枃偲偟
丂丂x+10y+100z+1000w=10000乧(1)
丂丂x+y+z+w=60乧(2)
偲偟偰丄(1)丆(2)傪枮偨偡0埲忋偺惍悢乮x,y,z,w乯偺慻偑懚嵼偡傞偲壖掕偡傞偲
丂丂(1)乚(2)丗9y+99z+999w=9940
偼丄(嵍曈)佭0乮mod9乯 偱偁傞偑丄(塃曈)佭4 (mod9) 偱偁傞偺偱柕弬
傛偭偰偙偺傛偆側慻傒偼懚嵼偟側偄
夝摎丒偦偺20
乮儁儞僱亅儉丗T_Tatekawa乯
寢榑偼乽巟暐偆偙偲偑弌棃側偄乿偱偡丏
傑偢10,000墌傪1,000墌嶥偩偗偱暐偆帠傪峫偊傞偲丆10枃昁梫偱偡丏
1,000墌嶥1枃傪100墌嬍偵椉懼偡傞偲丆崌寁19枃偱偡丏
偮傑傝9枃憹偊傑偡丏
2寘彫偝偄偍嬥偵椉懼偡傞偲99枃憹偊傞偺偱傾僂僩偱偡丏
偦偙偱1寘彫偝偄偍嬥偵椉懼偡傞帠傪峫偊傞偲丆椉懼偡傞偨傃偵偍嬥偼
9枃偢偮憹偊傑偡丏
偮傑傝丆10,000墌傪4庬椶偺壿暭偱巟暐偍偆偲偡傞偲丆枃悢傪9偱妱偭偨偲偒偺
偁傑傝偼偄偮傕摨偠乮梋傝1乯偱偡丏
偲偙傠偱60傪9偱妱傞偲梋傝偼6偱偡丏
偙偺偨傔4庬椶偺壿暭偱10,000墌傪巟暐偆帠偼弌棃傑偣傫丏
夝摎丒偦偺21
乮儁儞僱亅儉丗嶰妏掕婯乯
侾墌嬍丆10墌嬍丆100墌嬍丆1000墌嶥偺悢傪 x丆y丆z丆u 偲偡傞偲
丂丂丂x亄 y亄 z亄 u亖60 乧(1)
丂丂丂x亄10y亄100倸亄1000u亖10,000 乧(2)
(2)亅(1)丗 9(y亄11z亄111u)亖9,940 乧(3)
(1)(2)傪枮偨偡惍悢 x丆y丆z丆u 偑偁傞偲偡傞偲丆y亄11z亄111u 偼惍悢偱丆(3)傛傝
9,940 偼 9 偺攞悢偱側偗傟偽側傜側偄偑丆9,940 偼 9 偺攞悢偱偼側偄偺偱丆(1)(2)傪枮偨偡惍悢 x丆y丆z丆u 偼懚嵼偟側偄丅
傛偭偰丆侾墌嬍丆10墌嬍丆100墌嬍丆1000墌嶥傪崌傢偣偰60枃巊偭偰 10,000墌傪巟暐偆偙偲偼 偱偒側偄丅[徹柧椆]
僐儊儞僩
侾墌嬍丄10墌嬍丄100墌嬍丄1,000墌嶥傪崌傢偣偰60枃巊偭偰丄 偪傚偆偳丂10,000墌傪巟暐偆偙偲偼丄偱偒傑偣傫丅
懡偔偺曽偑丄惓偺惍悢傪俋偱妱偭偨偲偒偺忚梋乮梋傝乯偑偁傞偐偳偆偐偵拝栚偟偰丄 晄壜擻偱偁傞偙偲傪帵偟偰偔偩偝偄傑偟偨丅惓偺惍悢傪俋偱妱偭偨偲偒偺忚梋偼丄侽偐傜俉傑偱偺偄偢傟偐偵側傝傑偡丅 偙偺忚梋偵傛偭偰丄僌儖乕僾暘偗偡傞偲丄廳暋偺側偄俋偮偺廤崌偵暘偗傜傟傑偡丅 偙傟傪丄俋偺忚梋椶偲偄偄傑偡丅堎側傞忚梋椶偵懏偟偰偄傞惍悢偼丄摉慠丄摍偟偄偼偢偼偁傝傑偣傫偹丅
忚梋椶偲偄偊偽乽梛擔乿丄
偙傟偼俈偺忚梋椶偵儔儀儖傪偮偗偨傕偺偲峫偊傞偙偲偑偱偒傑偡丅
昞寁嶼僜僼僩Excel(Windows斉)偱偼丄擔晅偼丄1900擭侾寧侾擔傪僔儕傾儖抣乽侾乿偲偟偰丄弴偵斣崋偑妱傝怳傜傟偰偄傑偡丅
場傒偵2011擭10寧侾擔偼丄乽40817乿偱偡丅偙偺悢抣傪俈偱妱傞偲忚梋偼侽偱丄搚梛擔偱偡偐傜丄
擔晅偺僔儕傾儖抣傪俈偱妱偭偨梋傝偲丄梛擔偲偺娭學偼師偺傛偆偵側偭偰偄傞偲峫偊傜傟傑偡丅
丂丂忚梋侽丒丒丒搚梛擔
丂丂忚梋侾丒丒丒擔梛擔
丂丂忚梋俀丒丒丒寧梛擔
丂丂忚梋俁丒丒丒壩梛擔
丂丂忚梋係丒丒丒悈梛擔
丂丂忚梋俆丒丒丒栘梛擔
丂丂忚梋俇丒丒丒嬥梛擔
偙傟偵傛傞偲丄婎弨抣偱偁傞1900擭侾寧侾擔偼擔梛擔丄 巹偺抋惗擔偼栘梛擔偱偟偨丅(婰壇偵側偄偗偳丅)
場傒偵丄崱擔偺擔晅偲帺暘偺抋惗擔偺擔晅偲偱丄堷偒嶼傪偡傞偲丄
惗傑傟偰偐傜壗擔惗偒偰偄傞偐偑傢偐傝傑偡丅
*丂Excel偱偺僔儕傾儖抣偺昞帵偺巇曽
丂丂椺丗乽2011/10/1乿偲擖椡偟丄僙儖偺彂幃愝掕仺昞帵宍幃偱丄乽悢抣乿偲偟傑偡丅
 top
top