栤戣176丂朹偺暘妱
挿偝倎僙儞僠偺朹傪倐僙儞僠偲們僙儞僠偵暘妱乮倐亄們亖倎乯偡傞偵偼丄
倐亊們墌偺椏嬥偑偐偐傞偲偄偆丅
崱丄値僙儞僠偺朹偐傜僗僞乕僩偟偰丄挿偝偑帺慠悢偱偁傞傛偆偵暘妱傪孞傝曉偟丄
嵟屻偵侾僙儞僠偺朹値杮傪嶌傞偲偡傞丅
偙偺偲偒丄偳偺傛偆側夁掱傪宱偰暘妱偟偰傕丄偐偐傞椏嬥偼摨偠偱偁傞偙偲傪徹柧偣傛丅
栤戣偺弌揟
僉儏乕僩側悢妛柤嶌栤戣廤
彫搰姲擵挊
夝摎
乣摓拝弴偵偛徯夘偟傑偡乣
夝摎丒偦偺1
乮儁儞僱亅儉丗haya乯


夝摎丒偦偺2
乮儁儞僱亅儉丗儅僔儍乯
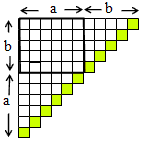
n僙儞僠偺偲偒偵偐偐傞椏嬥傪an偲偍偔丅
(柦戣)
乽an=(1/2)n(n-1)偱偁傝偐偮偳偺傛偆側夁掱傪宱偰暘妱偟偰傕丄偐偐傞椏嬥偼摨偠偱偁傞乿
偙偺柦戣傪悢妛揑婣擺朄傪梡偄偰徹柧偡傞丅
[1] n=1,2,3偺偲偒
暘妱偺夁掱偼1捠傝偺傒偱偁傞偺偱丄
丂丂a1 = 0(暘妱偡傞昁梫偑柍偄偐傜)
丂丂a2 = 1*1 = 1
丂丂a3 = 2*1 + 1*1 = 3
偲側傝柦戣偼惉傝棫偮
[2]n=4偺偲偒
暘妱偼丂4 仺 (2,2) 仺 (1,1,1,1)丂偲
丂丂丂丂丂4 仺 (3,1) 仺 (2,1,1) 仺 (1,1,1,1)
偺2捠傝偁傞丅
慜幰偺応崌丄a4 = a2 + a2 + 2*2 = 6
屻幰偺応崌丂a4 = a3 + 3*1 = 6
傛偭偰柦戣偼惉傝棫偮
[3]n=k丂(k=1,2,3,乧)丂埲壓偺偲偒慡偰偵偍偄偰柦戣偑惉傝棫偮偲壖掕偡傞丅
偙偺偲偒偵n=k+1傪峫偊傞丅
丂丂ak+1 = ak+1-m + am + (k+1-m)*m (m=1,2,乧,k)
丂 = (1/2)(k+1-m)(k-m) + (1/2)m(m-1) + (k+1-m)*m
丂 = (搑拞寁嶼徣棯)
丂= (1/2)(k+1)(k+1-1)
傛偭偰n=k+1偺偲偒傕柦戣偑惉傝棫偮丅
[4] [1]偐傜[3]偵傛傝悢妛揑婣擺朄偵傛傝柦戣偑恀偱偁傞偙偲偑徹柧偝傟偨丅
QED
夝摎丒偦偺3
乮儁儞僱亅儉丗偪傚傠傫偼懢懢乯
仚丂捈姶揑徹柧
1x1偺僞僀儖傪 廲 n屄丄墶n屄偵埲壓偺恾偺傛偆偵暲傋傞丅
n 乮 = a+b乯 傪 a 偲 b 偵暘妱偟偨偲偡傞偲丄
偦偺椏嬥乮a x b乯偼丄懢慄偱埻傢傟偨挿曽宍偺柺愊偵懳墳偡傞丅
巆偝傟偨晹暘偵偮偄偰傕暘妱傪孞傝曉偟峴偆偲丄椏嬥偼丄弴師丄惵怓偺僞僀儖晹暘偵懳墳偝傟傞丅
嵟廔揑偵挿偝侾僙儞僠偺朹偵暘妱偟偨応崌偼丄憤椏嬥偼丄恾拞偺惵怓僞僀儖偺憤柺愊偵懳墳偡傞丅
廬偭偰丄偳偺傛偆側夁掱偱暘妱偟偰傕丄椏嬥偼丄
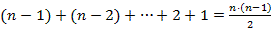 偲側傞丅
偲側傞丅
仚丂婣擺朄揑徹柧
挿偝 n 偺朹偺暘妱椏嬥偺憤榓偼丄
昁偢 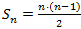 偲側傞偙偲傪徹柧偡傞丅
偲側傞偙偲傪徹柧偡傞丅
n=1 偺応崌偼惉棫偡傞丅n埲壓偺応崌丄惉棫偡傞偲偟偰丄n+1 偺応崌傪峫偊傞丅
n+1 偺朹傪嵟弶偵丂n+1-i偲丄i偵暘妱偟偨偲偡傞偲丄憤椏嬥偼丄
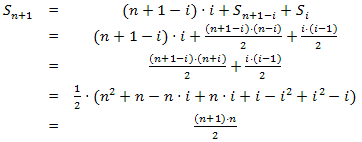
丂
偙傟偼丄i偺抣偵埶懚偣偢丄
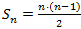 偺 n 傪丄n+1偲偟偨傕偺丅
偺 n 傪丄n+1偲偟偨傕偺丅
丂
傛偭偰丄n+1偺応崌傕徹柧偝傟偨丅
丂
夝摎丒偦偺4
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
n cm 偺帪偵偐偐傞椏嬥傪f(n) 偲偡傞偲乧
丂丂f(2)=1*1=1
丂丂f(3)=1*2+f(2)=2+1=3
丂丂f(4)=1*3+f(3)=3+2+1=6
丂丂丂or =2*2+2*f(2)=4+2*1=6
偦偙偱乧
f(n)=n(n-1)/2 偲峫偊傜傟傞偺偱偦偆壖掕偡傞偲乧
嵟弶丄擟堄 m屄偲n-m 屄偵暘偗偨応崌丄埲壓偺幃偱昞偝傟傞偑乧
f(n)=m*(n-m)+f(m)+f(n-m)
=m*n-m2+m(m-1)/2+(n-m)(n-m-1)/2
=m*n-m2+(m2-m+n2-2m*n+m2-n+m)/2
=(n2-n)/2
=n(n-1)/2
偐傜丄擛壗條偵暘妱偟偰傕嵟廔揑偵偼摨偠椏嬥偵側傞偙偲偑傢偐傞丅
夝摎丒偦偺5
乮儁儞僱亅儉丗偺偭偙傫乯
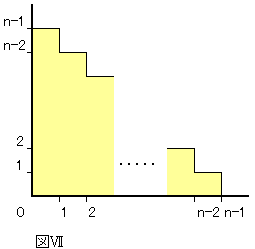
n僙儞僠偺朹傪1僙儞僠崗傒偱暘妱偟偰偄偔偲椏嬥偼
丂丂丂1丒(n-1)+1丒(n-2)+1丒(n-3)+丒丒丒丒丒+1丒3+1丒2+1丒1
丂丂=(1/2)丒n丒(n-1)墌偲側傞
廬偭偰n僙儞僠偺朹傪暘妱偡傞帪偺椏嬥偼乮偳偺傛偆側夁掱傪宱偰暘妱偟偰傕乯
丂丂丂(1/2)丒n丒(n-1)墌偱偁傞偙偲丒丒丒丒丒丒丒丒(1)丂
傪徹柧偡傟偽傛偄
嘥丂n=2偺帪丂(1)偼惉傝棫偮
嘦丂n=k偺帪丂(1)偑惉傝棫偮偲壖掕偡傞
丂丂偮傑傝k僙儞僠偺朹傪暘妱偡傞帪偺椏嬥偼
丂丂(1/2)丒k丒(k-1)墌偱偁傞偲壖掕偡傞
嘨丂(k+1)僙儞僠偺朹傪
丂丂m僙儞僠偲(k+1-m)僙儞僠偵暘妱偡傞偲乮m偼1埲忋k埲壓偺惍悢乯
丂丂偙偺暘妱偵偐偐傞椏嬥偼m丒(k+1-m)墌丄
丂丂m僙儞僠偺朹偺暘妱偵偐偐傞椏嬥偼嘦傛傝 (1/2)丒m丒(m-1)墌丄
丂丂(k+1-m)僙儞僠偺朹偺暘妱偵偐偐傞椏嬥偼嘦傛傝 (1/2)丒(k+1-m)丒(k-m)墌偩偐傜
丂丂崌傢偣偨椏嬥偼 (1/2)丒(k+1)丒k墌偲側傞
丂偙傟偼n=k偺帪丂(1)偑惉傝棫偮側傜偽
丂n=k+1偺帪傕惉傝棫偮偙偲傪帵偟偰偄傞
丂傛偭偰(1)偼徹柧偝傟偨
(1)偼椏嬥偑朹偺挿偝偵偺傒娭學偡傞偙偲傪帵偟偰偄傞
傑偨椏嬥偑侾捠傝偵掕傑傞偙偲偐傜柧傜偐側傛偆偵
椏嬥偼暘妱偺巇曽偵娭學偟側偄偙偲傪帵偟偰偄傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮徹柧廔傢傝乯
仸n僙儞僠偺帪偺椏嬥偑
丂nC2乮墌乯偵側傞偲偙傠偑柺敀偄偲巚偄傑偟偨
夝摎丒偦偺6
乮儁儞僱亅儉丗T_Tatekawa乯
n=2 偺帪丆1僙儞僠偺朹2杮偵暘妱偡傞偺偵偐偐傞椏嬥偼
丂丂丂1x1=1 墌丏
n=3 偺帪丆傑偢2僙儞僠偺朹偲1僙儞僠偺朹偵暘妱偟丆師偵2僙儞僠偺朹傪暘妱偡傞丏
崌寁偺椏嬥偼
丂丂丂2x1 + 1x1 = 3墌丏
n=4 偺帪丆嵟弶偺暘妱偑3僙儞僠偲1僙儞僠偐丆2僙儞僠2偮偐偱応崌暘偗丏
丂3僙儞僠偲1僙儞僠偺応崌丆嵟弶偵偐偐傞椏嬥偼 3x1 = 3墌丏
丂丂偙偺屻偵偐偐傞椏嬥偼3墌丏崌寁6墌丏
丂2僙儞僠2偮偵暘偗傞帪偺椏嬥偼 2x2 = 4墌丏
丂丂偙偺屻偵偐偐傞椏嬥偼 1x2=2墌丏崌寁6墌丏
丂偄偢傟傕偐偐傞椏嬥偼摨偠丏
偝偰丆n=k 偺帪丆偐偐傞椏嬥偑 k(k-1)/2 墌偲壖掕偡傞丏
n=k+1 偺帪丆傑偢m僙儞僠偲 (k-m+1)僙儞僠偺朹偵暘妱偡傞丏
偙偺帪偵偐偐傞椏嬥偼 m (k-m+1) 墌丏
偙偺屻偱偐偐傞椏嬥偼丆
m 僙儞僠偺朹傪嵟屻傑偱暘妱偡傞偺偵 m(m-1)/2 墌丏
(k-m+1) 僙儞僠偺朹傪嵟屻傑偱暘妱偡傞偺偵 (k-m)(k-m+1)/2 墌丏
埲忋傪崌寁偡傞偲
丂丂丂m (k-m+1) + m(m-1)/2 + (k-m)(k-m+1)/2 = k(k+1)/2 墌
傛偭偰丆n=k+1 偺帪偱傕壖掕偑惉傝棫偮丏
埲忋偐傜丆n 僙儞僠偺朹偺暘妱偵偐偐傞椏嬥偼暘妱偺曽朄偵傛傜偢
丂丂丂n(n-1)/2 墌
偱偁傞丏
夝摎丒偦偺7
乮儁儞僱亅儉丗MVH乯
乲夝摎乴
寢榑偐傜弎傋傑偡丅
杮栤偵偍偄偰丄偳偺傛偆側夁掱傪宱偰暘妱偟偰傕丄偐偐傞椏嬥偼丄(n亅1)n/2 墌偱偡丅
偙偺偙偲傪丄帺慠悢n偵娭偡傞悢妛揑婣擺朄偵傛傝丄帵偟傑偡丅
鶣乯n=1偺偲偒丄帺柧偱偡丅
鶤乯n埲壓偺慡偰偺帺慠悢偱惉棫偡傞丄偲壖掕偟傑偡丅
崱丄(n+1)僙儞僠偺朹傪丄a僙儞僠偲b僙儞僠偵暘妱偡傞偲偟傑偡乮n+1=a+b乯丅
偡傞偲丄壖掕偵傛傝丄嵟屻偵侾僙儞僠偺朹傪n+1杮嶌傞傑偱偵偐偐傞椏嬥偼丄
丂丂ab+(a亅1)a/2+(b亅1)b/2=a(n+1亅a)+(a亅1)a/2+(n+1亅a亅1)(n+1亅a)/2=n(n+1)/2
偱偡偐傜丄n+1偺偲偒傕惉棫偟傑偡丅
埲忋鶣乯鶤乯偵傛傝丄擟堄偺帺慠悢値偱惉棫偡傞偙偲偑帵偝傟傑偟偨丅
廬偭偰丄戣堄偼帵偝傟傑偟偨丅乮徹廔乯仭
夝摎丒偦偺8
乮儁儞僱亅儉丗揮埵斀墳乯
挿偝値僙儞僠偺朹傪抂偐傜倠僙儞僠偱暘妱偡傞偲丄偦傟偧傟倠僙儞僠丄乮値亅倠乯僙儞僠偺朹偵側傝丄
暘妱偺椏嬥偼倠乮値亅倠乯偱昞偝傟傞丅扐偟丄倠偼丄侾亝倠亝値亅侾傪枮偨偡惍悢偱偁傞丅
峏偵丄倠乮値亅倠乯傪挿曽宍乮傑偨偼惓曽宍乯偺柺愊偲偟偰懆偊傞偲丄
倠丄値亅倠傪俀幉偲偡傞嵗昗宯偵傛傝丄暘妱偡傞埵抲偲柺愊傪埲壓偺捠傝昞尰偱偒傞丅
偝偰丄値亖俆偲偟偰嬶懱揑偵峫偊偰傒傞丅
倠亖侾丆俀丆俁丆係偱暘妱偟偨応崌偵惗惉偡傞挿曽宍偼丄偦傟偧傟恾嘥乣嘩偺捠傝偱偁傞丅
扐偟丄偙傟傜偺挿曽宍偼嵟弶偵朹偑暘妱偝傟偨帪偵惗惉偡傞傕偺偱偁傝丄擇夞栚埲崀偵暘妱偝傟偨
応崌偵偼丄愭峴偟偰暘妱偝傟偨朹偺挿偝偵懳墳偟偨柺愊偑尭彮偡傞偙偲偵側傞丅
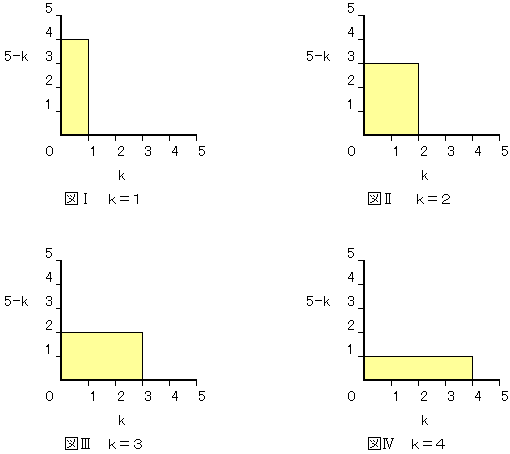
椺偊偽丄嵟弶偵倠亖侾偱暘妱偟偰丄懕偄偰倠亖俀丄俁丄係偱弴師暘妱偡傞偲丄恾嘪偵帵偟偨捠傝偲側傞丅
暘妱偺弴彉偵墳偠偰丄恾嘦乣嘩偺挿曽宍偺廳側傞晹暘偺柺愊偑尭彮偡傞偙偲偵側傝丄
嵟廔揑偵巆偭偨奺挿曽宍偺俀曈偺挿偝偑暘妱捈屻偺擇偮偺朹偺挿偝偵懳墳偟偰偄傞丅
摨條偵丄嵟弶偵倠亖俁偱暘妱偟丄懕偄偰倠亖俀丄侾丄係偲弴師暘妱偟偨応崌傪恾嘫偵帵偟偨丅
挿曽宍偺柺愊偑堎側傞傕偺偑偁傞偑丄偦傟傜偺巐妏宍偺柺愊偺憤榓偼恾嘪偲恾嘫偱偼摨偠偵側傞丅
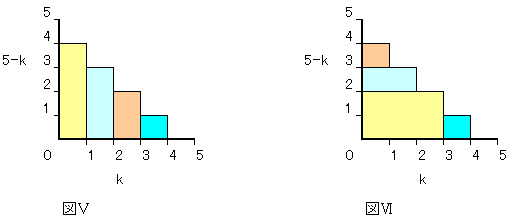
埲忋偺峫嶡偵傛傝丄挿偝値僙儞僠偺朹傪挿偝侾僙儞僠偺値杮偺朹偵暘妱偡傞偺偵梫偡傞椏嬥偺崌寁偼丄
恾嘮偵帵偟偨恾宍偲偟偰昞尰偱偒丄朹偺挿偝値偵埶懚偟偰偄傞丅
側偍丄偙偺恾宍偺撪晹偺愗傝暘偗曽偼丄朹傪暘妱偡傞埵抲偲暘妱偺弴彉偵傛傝堦堄揑偵寛傑傞丅
傛偭偰丄挿偝値僙儞僠偺朹偺暘妱偵梫偡傞慡椏嬥俽偼丄壓婰偺幃偱梌偊傜傟傞丅
丂丂俽亖侾亄俀亄俁亄丒丒丒亄乮値亅侾乯亖乮値俀亅値乯乛俀
夝摎丒偦偺9
乮儁儞僱亅儉丗Ryu1128乯
偡偖偵夞摎偑摼傜傟傞偺偵偦偺夞摎傪昞尰偡傞偙偲偑弌棃側偄擄栤偩偲巚偄傑偡丅
愭偢丄嵍懁偐傜侾偯偮愜偭偨応崌傪峫偊傑偟偨丅
偦偺帪偺抣抜偼壓恾愒偱埻傑傟偨柺愊偵側傝傑偡丅
懄偪丄値乮値-1乯/2偱偡丅

師偵柍嶌堊偵愜偭偨帪傪峫偊傞偲偳偺傛偆側弴偱愜偭偨偲偟偰傕壓恾偺庨慄傪挻偊傜傟側偔妿偮杽傔恠偔偝側偗傟偽丄 慡偰傪侾偵偡傞偙偲偑弌棃側偄偙偲偑傢偐傝傑偡丅 側偤側傜丄侾夞栚偵愜傞埵抲傪嵍偐傜倫偲偡傞偲塃懁偼値-倫偲側傝忋恾L偵忔傝傑偡丅埲壓僌儔僼忋丄揰乮倫丄値-倫乯傛傝塃懁忋懁偼摨偠棟桼偱杽傔恠偔偝傟側偗傟偽側傜側偄偐傜偱偡丅乮乮倫丄倫乯媦傃乮値-倫丄値-倫乯偺僌儔僼偵婣寢偝傟傞偨傔丅乯

戙悢揑偵夝偙偆偲偟偨偺偱偡偑柪楬偵偼傑傝崬傫偱丄偳偆傕偆傑偔峴偐偢忋婰偑徹柧偲偼偄偊側偄偙偲偼帺妎偟偰偄傑偡偑偲傝偁偊偢捈姶偲偟偰偼庴偗擖傟傜傟傞偺偱偼側偄偐偲峫偊搳峞偟傑偡丅
夝摎丒偦偺10
乮儁儞僱亅儉丗atsuhiro乯
偳偺傛偆側愗傝曽偵懳偟偰傕偐偐傞椏嬥
丂丂P(n)=(n-1)n/2丒丒丒仏
偱偁傞偙偲傪悢妛揑婣擺朄偵傛傝帵偡
鶣)n=1偺偲偒
丂丂P(1)=0丂傛傝丂仏丂惉棫
鶤乯n亝k (亞1) 偺偲偒丂仏丂傪壖掕
丂n=k+1偺偲偒侾夞栚偺暘妱偱a偲b偵暘偐傟偨偲偡傞偲(a+b=k+1丆a,b伕N)
丂丂丂P(k+1)=ab+P(a)+P(b)
丂丂=ab+(a-1)a/2+(b-1)b/2 (佹壖掕)
丂丂={(a+b)2,/sup>-(a+b)}/2
丂丂=(k+1)k/2
丂傛偭偰n亖k+1偺偲偒傕?惉棫
鶣丆鶤傛傝擟堄偺n偵懳偟偰?惉棫(Q.E.D)
夝摎丒偦偺11
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
倄亖亅倃亄俶丂偲偟傑偡丅
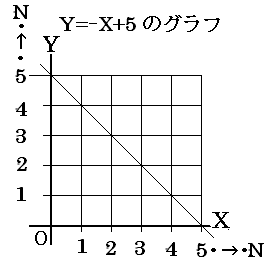
倄亖巆傝偺挿偝丂倃亖愗傞挿偝丂俶亖朹偺挿偝
椺偲偟偰挿偝俆cm偲偟偰
(1)
丂侾夞栚侾噋偱愗傞偲丂巆傝Y=-1+5=係噋丂庤悢椏偼侾亊係亖係墌
丂俀夞栚俀噋偱愗傞偲丂庤悢椏偼俀亊俀亖係墌
丂俁夞栚偦傟偧傟侾噋偱愗傞偲侾亊侾亊俀亖俀墌
丂崌寁庤悢椏偼係亄係亄俀亖侾侽墌
(2)
丂侾夞栚俀噋偱愗傞偲俀噋偲俁cm偵側傞庤悢椏偼俀亊俁亖俇墌
丂俀夞栚俀噋傪侾噋偯偮偵愗傞偺偱庤悢椏偼侾亊侾亖侾墌
丂俁夞栚俁cm傪侾噋偲俀噋偵偟傑偡丅庤悢椏偼侾亊俀亖俀墌
丂係夞栚俀噋傪侾噋偯偮偵偟傑偡偺偱侾亊侾亖侾墌
丂崌寁庤悢椏偼俇亄侾亄俀亄侾亖侾侽墌
(3)
丂侾夞栚俁cm偱愗傞偲俁cm偲俀噋偵側傞庤悢椏偼俁亊俀亖俇墌
丂俀夞栚俁cm傪侾噋偲俀噋偵愗傞庤悢椏偼侾亊俀亖俀墌
丂俁夞栚偼侾夞栚偲俀夞栚偱弌棃偨俀噋傪侾噋偱愗傞丅
丂庤悢椏偼侾亊侾亊俀亖俀墌
丂庤悢椏崌寁偼俇亄俀亄俀亖侾侽墌
(4)
丂侾夞栚偼係噋偱愗傞偲庤悢椏偼侾亊係亖係墌
丂巆偭偨係噋傪俀噋偱愗傞偲庤悢椏偼俀亊俀亖係墌
丂俀噋偺朹傪偦傟偧傟侾噋偵愗傞偲庤悢椏偼侾亊侾亊俀亖俀墌
丂庤悢椏偺崌寁偼係亄係亄俀亖侾侽墌
丂偙偺傛偆偵偳偺條側埵抲偐傜愗偭偰傕摨偠庤悢椏偵側傝傑偡丅
忋婰偺捠傝恾傪傒偰庤悢椏偼Y=亅X亄俆偺僌儔僼偲Y亖侽丄 X=侽偵埻傑傟傞拞偵偁傞瀍偺悢偱偁傞偙偲偑暘偐傝傑偡丅
廬偭偰丅N噋偺朹偺応崌偺庤悢椏偼師偺寁嶼幃偵側傝傑偡丅 庤悢椏=乮N亊N亅N)亐俀偲側傝傑偡丅壗張偐傜愗偭偰傕摨偠庤悢椏偵側傞帠偑徹柧弌棃傑偟偨丅
夝摎丒偦偺12
乮儁儞僱亅儉丗Part Marty乯
侾乯ncm偺朹傪1cm偲(n-1)cm偵暘妱偡傞偲1X(n-1)=n-1,
(n-1)cm偺朹傪1cm偲(n-2)cm偵暘妱偡傞偲1X(n-2)=n-2,
嵟屻偵侾僙儞僠偺朹値杮傪嶌傞偲偡傞丅
1偐傜n-1傑偱偺懌偟嶼儼側偺偱丄nX(n-1)/2偱偁傞丅
2)偳偺傛偆側夁掱傪宱偰暘妱偟偰傕丄偐偐傞椏嬥偼摨偠偱偁傞偙偲傪徹柧偣傛丅
ncm偺朹傪(n-m)cm偲m cm偵暘妱偡傞偲(n-m)Xm墌
ncm偺朹傪侾僙儞僠偺朹偵暘妱偡傞偲mx(m-1)/2墌
(n-m)cm偺朹傪侾僙儞僠偺朹偵暘妱偡傞偲(n-m)X(n-m-1)/2墌
(n-m)Xm+mX(m-1)/2+(n-m)X(n-m-1)/2=nx(n-1)/2
侾乯偺曽朄偱暘妱偟偨抣抜偲摨偠偵側傞丅
廬偭偰丄偳偺傛偆側夁掱傪宱偰暘妱偟偰傕偐偐傞椏嬥偼摨偠偱偁傞丅
夝摎丒偦偺13
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
仠 n僙儞僠偺朹偐傜1僙儞僠偺朹n杮傪嶌傞偺偵昁梫側偍嬥傪f(n)墌偲偟傑偡丅
嬶懱揑偵丄偄偔偮偐挷傋傑偡丅
丂丂f(2)亖1亊1亖1
丂丂f(3)亖1亊2亄f(2)亖2亄1亖3
f(4)偼2捠傝偺応崌傪挷傋傑偡丅
丂丂丒1偲3偵暘偗傞偲偒丄
丂丂丂f(4)亖1亊3亄f(3)亖3亄3亖6
丂丂丒2偲2偵暘偗傞偲偒丄
丂丂丂f(4)亖2亊2亄2亊f(2)亖4亄2亖6
傛傝f(4)亖6偱偡丅
仠 n僙儞僠偺朹傪1僙儞僠偢偮暘妱偟偰偄偔偲偡傞偲丄
丂丂f(n)亖1亊(n亅1)亄f(n亅1)傛傝
丂丂f(n)亖f(n亅1)亄n亅1
偲偄偆慟壔幃偑峫偊傜傟傑偡丅
偙傟偼丄
丂丂f(n)亖f(n亅1)亄n亅1
丂丂f(n亅1)亖f(n亅2)亄n亅2
丂丂f(n亅2)亖f(n亅3)亄n亅3
丂丂丂ゥゥゥ
丂丂f(4)亖f(3)亄3
丂丂f(3)亖f(2)亄2
丂丂f(2)亖1
偲暲傋偰丄崌寁偟惍棟偡傞偲丄
丂丂f(n)亖1亄2亄3亄ゥゥゥ亄(n亅3)亄(n亅2)亄 (n亅1)亖1乛2亊n(n亅1)
偲側傝傑偡丅
仠 n僙儞僠偺朹傪暘妱偟偰1僙儞僠偺朹n杮傪嶌傞偺偵昁梫側偍嬥偼夁掱偵娭學側偔堦掕偱偁傞偙偲傪挷傋傑偡丅
丂f(n)亖1乛2亊n(n亅1)丂偲壖掕偟傑偡丅
丂丂丒n亖2偺偲偒丄
丂丂丂f(2)亖1乛2亊2(2亅1)亖1偱忋偺寢壥偲堦抳偟傑偡丅
丂丂丒n偺偲偒偺壖掕傪摜傑偊偰丄n亄1偺偲偒傪挷傋傑偡丅
丂丂丂n亄1僙儞僠偺朹傪k僙儞僠偲n亄1亅k僙儞僠偵暘偗偨偲偡傞偲丄
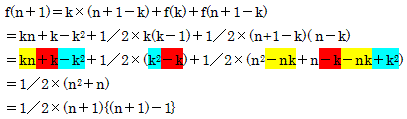
偲側傝丄n亄1僙儞僠傪偳偆暘偗偰傕寢壥偼摨偠偵側傝傑偡丅
夝摎丒偦偺14
乮儁儞僱亅儉丗傑乕傝傫倎値倓偝偲傝傫乯
 挿偝偑倠們倣偺朹偑侾們倣挿偔側偭偨偲偒偵丄憹壛偡傞椏嬥偵偮偄偰峫偊傞丅
挿偝偑倠們倣偺朹偑侾們倣挿偔側偭偨偲偒偵丄憹壛偡傞椏嬥偵偮偄偰峫偊傞丅
"倠 偺晹暘傪偳偺傛偆側庤弴偱偽傜偽傜偵偟偰傕丄塃抂偺侾們倣傪娷傓朹傪愗傞偨傃偵丄
愗傝岥偺嵍懁偺挿偝偵摍偟偄椏嬥暘偑憹壛偡傞偙偲偵側傞
乮塃抂偺侾們倣傪娷傑側偄朹傪愗傞偲偒偼椏嬥憹偵娭學偟側偄乯丅
傛偭偰丄椏嬥憹暘偺憤榓偼忢偵乮倎亄倐亄們亄丒丒丒亖倠側偺偱乯倠墌偱偁傞丅
"
偙偙偱丄俀們倣偺朹傪愗傞曽朄偼侾庬椶乮侾們倣亊侾們倣乯側偺偱侾墌偱寛傑偭偰偄傞丅
偮傑傝k亖俀們倣偺偲偒偵侾墌偱丄侾們倣挿偔側傞偨傃偵尦偺挿偝偺抣抜暘偑愗傝曽偵傛傜偢堦掕偱憹壛偡傞丅
偟偨偑偭偰丄偁傞挿偝値們倣偺朹傪愗傞椏嬥偼丄愗傝曽偵傛傜偢堦掕偵側傞丅
* 拞妛侾擭惗偲偄偆偙偲偱偡偐傜丄傑偩乽悢妛揑婣擺朄乿傪妛峑偱曌嫮偟偰偄側偄偲巚偄傑偡偑丄 偦偺峫偊曽偑昞尰偝傟偰偄傞偲巚偄傑偡丅乮俰乯
夝摎丒偦偺15
乮儁儞僱亅儉丗柪巕偺梇擫乯
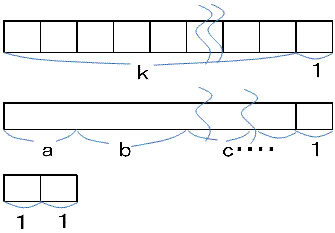
挿偝倎僙儞僠偺朹傪倐僙儞僠偲們僙儞僠偵暘妱乮倐亄們亖倎乯偡傞偵偼丄倐亊們墌偺椏嬥偑偐偐傞偲偄偆丅
傑偢丄倎恖偐傜俀恖偺慻傪慖傇偙偲傪峫偊傛偆丅摉慠倎俠俀捠傝偺慻傒崌傢偣偑偁傞丅
偝偰丄倎恖傪倐恖偲們恖偺僌儖乕僾俀偮偵暘妱偟偨偲偡傞丅
偙偺応崌丄倎恖偐傜俀恖偺慻傪慖傇曽朄偑丄埲壓偺3偮偵廳暋傗傕傟偑側偔暘妱偝傟傞偙偲偵側傞丅
丂偁丏倐恖偺僌儖乕僾偲們恖偺僌儖乕僾偐傜侾恖偢偮慖傇
丂偄丏倐恖偺僌儖乕僾偐傜俀恖慖傇
丂偆丏們恖偺僌儖乕僾偐傜俀恖慖傇
忋婰乽偁乿偺慖傃曽偼倐亊們捠傝偱偁傞偺偱丄
乽値僙儞僠偺朹偐傜僗僞乕僩偟偰丄挿偝偑帺慠悢偱偁傞傛偆偵暘妱傪孞傝曉偟丄
嵟屻偵侾僙儞僠偺朹値杮傪嶌傞乿
傑偱偵偐偐傞旓梡偼丄倎恖偐傜俀恖偺慻傪慖傇慖傃曽偺悢偲侾丗侾偵懳墳偡傞丅
傛偭偰丄乽偳偺傛偆側夁掱傪宱偰暘妱偟偰傕丄偐偐傞椏嬥偼摨偠偱偁傞乿丅
夝摎丒偦偺16
乮儁儞僱亅儉丗嶰妏掕婯乯
n 僙儞僠偺朹傪 1 僙儞僠亊 n 杮偵暘妱偡傞偺偵偐偐傞椏嬥傪 f (n) 墌偲偡傞偲丆戣堄傛傝
丂丂丂f (m亄n)亖mn亄f (m)亄f (n) 乧(1)
(1)偼 n亖1 偱惉傝棫偮偙偲偑昁梫偩偐傜
丂丂丂f (m亄1)亖m亄f (m)亄f (1)
丂丂丂丂丂丂丂丂亖m亄f (m) 丂(佹 柧傜偐偵 f (1)亖0 ) 乧(2)
(2)傛傝丂f (m)亖m(m亅1)/2 乧(3)
媡偵
丂丂丂(m亄n)(m亄n亅1)/2亖mn亄m(m亅1)/2亄n(n亅1)/2
傛傝丆(3)偼擟堄偺 m丆n 偵偮偄偰(1)傪枮偨偡丅
埲忋傛傝強梫偺椏嬥偼 (3) 偱丆偙傟偼丆暘妱偺巇曽偵埶傜側偄丅丂[徹柧椆]
夝摎丒偦偺17
乮儁儞僱亅儉丗塝壀乯
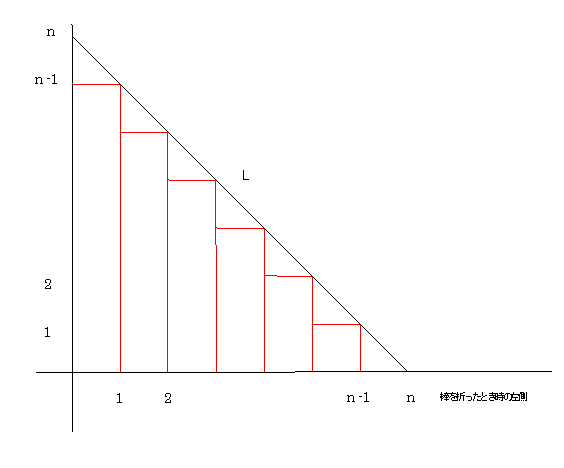
偙偺栤戣偼恾宍揑偵懆偊傞偲丄庱旜椙偔夝寛偡傞丅
傑偢丄捈岎嵗昗傪弨旛偟丄y=-x+n(0亝x亝n) 乧乮仸乯傪n僙儞僠偺朹偵尒棫偰傞丅
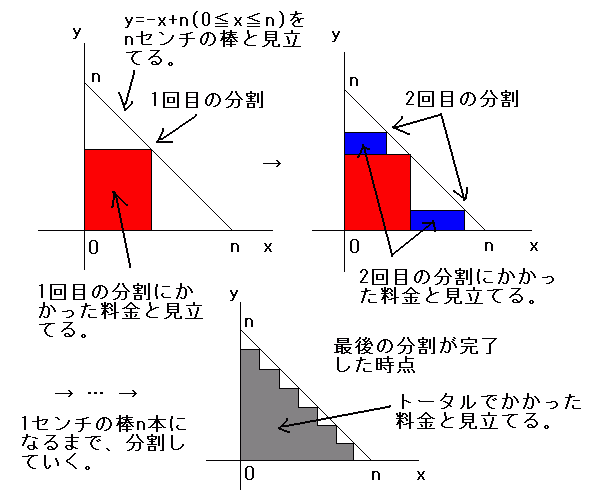
偮偓偵丄乮仸乯忋偺奿巕揰傪朹傪暘妱偡傞揰偲尒棫偰丄偦偺揰傪1偮偺捀揰偲偟嵗昗幉偲偱埻傑傟偨挿曽宍傪嶌傞丅
偡傞偲丄挿曽宍偺柺愊偑丄偦偺暘妱偵偐偐傞椏嬥偲懳墳偡傞偙偲偵側傞丅
偙偺偲偒丄乮仸乯忋偺奿巕揰傪1偮偺捀揰偲偟嵗昗幉偲偱埻傑傟偨
乮傑偨偼曈偑嵗昗幉偲暯峴偲側傞乯挿曽宍傪壜擻側尷傝嶌傞偲丄
嵟屻偵偱偒傞恾宍偼丄偳偺傛偆側夁掱傪宱偰傕恾偵帵偟偨奒抜忬偵側傞偙偲偐傜丄暘妱偺夁掱偵傛傜偢偐偐傞椏嬥偼堦掕偱偁傞丅乮徹柧廔乯
僐儊儞僩
挿偝値偺朹傪暘妱偡傞偺偵昁梫側椏嬥偺憤悢偼丄椺偊偽抂偐傜侾偢偮愗偭偰偄偔偙偲傪峫偊傟偽媮傔傞偙偲偑偱偒傑偡丅
丂丂値(値亅侾)/2
偱偡丅偟偐偟丄偙偺栤戣偼丄偙傟傪媮傔傞偙偲偵偁傞偺偱偼側偔(廬偭偰丄媮傔偰偄側偔偰傕俷俲偱偡)丄
乽偳偺傛偆側夁掱傪宱偰暘妱偟偰傕偐偐傞椏嬥偑摨偠乿偲偄偆偲偙傠傪帵偡昁梫偑偁傝傑偡丅
懡偔偺曽偑丄擟堄偺暘妱傪憐掕偟偰丄偦傟偵婑傜偢偵椏嬥偑堦掕偱偁傞偙偲傪帵偟偰偔偩偝偄傑偟偨丅
傑偨丄暘妱偺椏嬥偼丄挿曽宍偺柺愊偱昞偡偙偲偑偱偒傑偡丅
揮埵斀墳偝傫懠丄壗恖偐偺曽偑偙偺偙偲傪
帵偟偰偔偩偝偭偰偄傑偡丅揮埵斀墳偝傫偺恾傪偍庁傝偟偰丄
暿側昞尰傪偡傞偲丄
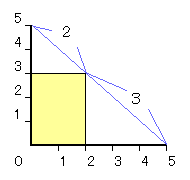
椺偊偽値亖俆偺朹傪暘妱偡傞偺偼丄忋偺恾偺傛偆偵丄 幬曈偑俆併俀偺捈妏嶰妏宍偺幬曈傪俆摍暘偡傞偙偲偵憡摉偡傞偲峫偊傜傟傑偡丅 偦偟偰丄椺偊偽丄値亖俀偲値亖俁偵暘妱偡傞応崌偼丄俀亊俁偺椏嬥偑偐偐傝傑偡偑丄 偙傟偑恾偱偼丄挿曽宍偺柺愊偵側傞傢偗偱偡丅 偦偟偰丄偝傜偵丄値亖俀偲値亖俁偺暘妱傪偟傑偡偑丄 偦傟偼丄幬曈偑俀併俀偲俁併俀偺捈妏嶰妏宍偺幬曈傪暘妱偡傞偙偲傪堄枴偟傑偡丅 廬偭偰丄嵟廔揑偵偼丄偳偺傛偆側宱楬傪偨偳偭偰傕 揮埵斀墳偝傫偺偙偺恾偺傛偆偵側傞偲偄偆傢偗偱偡丅

 top
top