問題175 ダーツ投げの問題
１辺が30センチの正方形のダーツ板がある。このダーツ板に10本のダーツを投げたら、
すべて板にささったとする。
このとき、少なくとも２本のダーツの距離は15センチ未満であることを証明せよ。
問題の出典
キュートな数学名作問題集
小島寛之著
解答
解答・その1
（ペンネ−ム：三角定規）
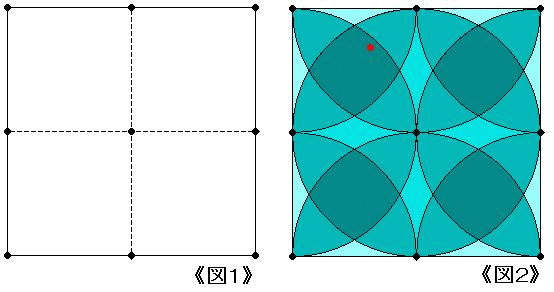
《図１》 のように，正方形の４頂点，４辺の中点および中心に９本のダーツが刺さったとき，
どの２本の間隔も 15 cm 以上になる。
９点をそれぞれ中心とする半径 15 cm の円を正方形内に描くと，９個の円内の点は
《図２》 のように正方形を埋め尽くしてしまう(着色部分)。
よって，10本目のダーツが正方形内に刺ささるとき，それと少なくともどれか１本との間隔が 15 cm 以内になる。（証明了）
解答・その2
（ペンネ−ム：転位反応）
題意は、全てのダーツの距離を１５センチ以上にすることができないことと同値である。
９本のダーツについては、１辺が30センチの正方形のダーツ板を１辺が１５センチの
正方形に４分割して、ダーツの距離を１５センチとして配置することができる。
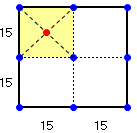
ところが、１０本目のダーツについては、ダーツ板のどの位置に刺さったとしても、
距離を15センチ以上とすることはできない。
下図の通り、小正方形の中央に刺さった場合に最大値を取り、１５×√２／２ ＜１５
∴ 全てのダーツの距離を１５センチ以上にすることができない。
∴ 少なくとも２本のダーツの距離は15センチ未満である。
解答・その3
（ペンネ−ム：Ryu1128）
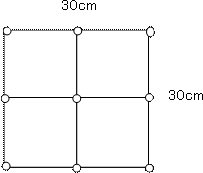
30ｃｍの的を15ｃｍの格子に切ります。格子の各点にダーツの刺さった位置を配置します。
その結果9本まではお互いの距離を15ｃｍ確保できます。
9本の配置はこれ以外に無いことは、各点から半径15ｃｍの円を書くことで容易に確かめられます。
どの1点（または2点以上）を移動しても互いの距離は15ｃｍ未満となる点が生じてしまいます。
次に題意から少なくとも2本のダーツの距離は15ｃｍ未満となること。
これには引っかかりました。なぜならここにダーツを投げると格子線上に当たったとしても
少なくとも3本となりますから・・・。
ここで、現実と抽象的な数学の違いがありますね。そもそも格子点上にダーツが刺さる確率は0ですから、幾何の問題として考えなければならないのを、ついつい現実のダーツを想像して考えていました。
少なくとも2本というのは、10本目が再度各格子点上に刺さった場合となります。
つまりその2点間の距離は0ですね。そして10本目は9通りあります。
3本であれば格子線上にある点全てと、各点から半径15ｃｍの円から逃れる点も範囲に入ります。
解答・その5
（ペンネ−ム：もげぴ）
「１辺が30センチの正方形のダーツ板に10本のダーツを投げる」場合に，
「10本すべてが板にささったならば，板に刺さっているダーツのうち少なくと
も２本のダーツの距離は15センチ未満である。」との命題を証明する問題。
この命題の対偶は，「板に刺さっている全てのダーツが相互に15センチ以上離
れているならば，板に刺さっているダーツは１０本未満（９本以下）である」となる。
さて，１辺が30センチの正方形のダーツ板に，ダーツを相互に15センチ以上離して刺すとすると，
最大で９本のダーツが刺さる（１辺１５センチメートルの正方形４枚による平面充填。
１辺15センチメートルの正三角形では，ダーツ板に最大６枚（ダーツ８本）しか配置できない）。
証明すべき命題の対偶が真なので，この命題も真となる。（以上）
・・・・・・・・・・・・・・・・・・・・・・・・
実は，類似の問題の検討（正しいかどうか分かりません）を見たことがありました。要旨は
「設題の正方形を１０センチ四方の正方形９つに分割し，１０本のダーツを指すと，
少なくとも１つの正方形には２本以上のダーツが刺さらざるを得ず，その
２本のダーツの距離は最長でも対角線の10ルート2（＝1.4142・・・）である」
というものです。
いまひとつしっくり来ないので，自分なりに考えたのが上記の回答ですが，
正解となるかどうかはさておき，「ダーツを相互に15センチ以上離して刺すとす
ると，最大で９本のダーツしか刺さらない」点をもう少しきちんと説明しないといけないような気もしています。
解答・その6
（ペンネ−ム：ＣＨ４）
正方形を対辺の中点同士を結んで四等分します。
このとき正方形は90°ずつ回転させても全て同じ図形になるので、仮に条件を満たしながら点10個を打つことができるとき、そのパターンには少なくとも一つ、回転させても形の変わらないものがあるはずです。
ここで、左上の正方形に一つ点を打ちます。（最初の図）
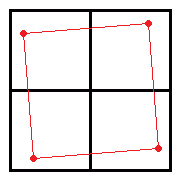このとき、他の正方形には二番目の図のように点が打たれます。
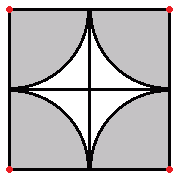
１）赤い正方形の外側に点が打てないとき
赤い正方形の外側の部分はないものと考えてよいので、赤い正方形において、
題意を満たすように10個の点を打つことになります。
これが可能であることは、黒い正方形の各頂点に点を打ったときに可能であるための十分条件です。
よって、各頂点に点を打って考えられます。
２）赤い正方形の外側に点が打てる時
赤い正方形を作った後、その外側に点を打つことは、先に赤い正方形の外側部分に点を打ち、そのあと内側に赤い正方形を作っても同じことなので、先に外に点を打つことを考えます。
１）、２）より初めは各頂点に4点を打つことになります。
各頂点から半径15cmの範囲には点を打てないので、三番目の図の白い範囲で考えます。
左上の部分に一つ点を打つとき、他の正方形には四番目の図のように点が打たれます。
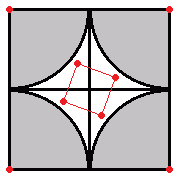このとき、上の正方形の時と同様に考えて、四点は元の正方形の各辺の中点に打って考えられます。
このとき、五番目の図のように、元の正方形の中心に一つ点を打つのが限界です。
つまり、最適な条件で点を打ったとき、題意を満たしながら打てる点の最大の数は９つです。
10個目の点を打とうとしたとき、それは必ずどこかの点を中心とした半径15cmの円の内部に打たれることとなります。
よって、一辺が30cmの正方形に10個の点を打ったとき、少なくとも二つの点の距離は15cm未満となります。（証明終）
解答・その7
（ペンネ−ム：teki）
この問題、
「１辺４５ｃｍの正方形の中に直径１５ｃｍの円がいくつ入るか？」
という問題に置き換えた方が解きやすいです。
（題意と完全に同値ではありませんが、この数値設定ではほぼ同値です。）
さて、１辺４５ｃｍの正方形の中には、直径１５ｃｍの円が最大で９個入ります。
（各段３個で３段が最大です。）
ここに１０個目の円を入れることは、どうやっても不可能です。
よって、１辺３０ｃｍの正方形の中に１０個の点を取れば、必ず１５ｃｍ未満の２点があります。
（先ほど完全に同値ではないと書いたのは、適当な細長い長方形の場合、
ｎ個、ｎ−１個、ｎ個・・・・・・という積み上げ方をすれば、
１段余分に取れる場合があるので、単純の各段ｎ個を積み上げるより多くの円が収まる可能性があるからです。
ところが、３×３段程度だと、こういった積み上げ方ができないため最大で９個が限界です。）
＜別解＞（こちらの方がわかりやすいですね。）
１辺３０ｃｍの正方形を１辺１０ｃｍの正方形に９分割します。
すると、分割された正方形の中にダーツが２本あるものが必ず１個以上あります。
（これは鳩の巣理論で明白ですよね。）
小正方形の中に２本のダーツがある場合、その２本の距離は小正方形の対角線の長さより
長くなることはないので、２本間の距離は
√２×１０＝１４．１４２・・・・・
を超えません。
解答・その8
（ペンネ−ム：スモークマン）
鳩の巣で有名かなぁ...?
10x10 が9個あるので...
どれか１区画には2本の矢が刺さってる...
10x10の中で一番離れているときでも...10x√2=14.142...＜15
解答・その9
（ペンネ−ム：のっこん）
正方形の的をたて・横それぞれ３等分すると
一辺の長さが１０cmの小正方形が９個できる。
１０本のダーツがこの的に当っているのだから
少なくとも２本が当っている小正方形が存在する。
一辺の長さが１０cmの正方形内に２点があれば
その距離は
最も離れていても１０√２＝１４．１４２・・・（cm）だから
少なくとも２本のダーツの距離は１５cm未満である。
解答・その10
（ペンネ−ム：迷子の雄猫）
1.
１辺が30センチの正方形のダーツ板を縦横それぞれ3等分すると、１辺が10センチの正方形の区画が9つできる。
2.
このダーツ板に10本のダーツを投げたら、すべて板にささったとする。
このとき、少なくとも２本のダーツが刺さっている区画が少なくとも1つ存在する。
3.
１辺が10センチの正方形の区画の中にとった任意の2点の距離は対角線の長さを超えない。
対角線の長さが14.2センチ未満であるので、任意の2点の距離は15センチ未満である。
以上、証明終わり。
じゃ、２本のダーツの最小距離を、最大どのくらいに出来るのか？
以下の組み合わせで11にすることは出来るので、おそらく11.03くらいだろうと予想してます。
(11.07,11.07) (18.93,18.93) (0,0) (11,0)(22,0) (0,11) (0,22) (19,30) (30,19) (30,30)
解答・その11
（ペンネ−ム：ちょろんは太太）
１辺が30センチの正方形を、1辺が10センチの正方形9個に分割する。
10本のダーツが当たったとすれば、9個の正方形のうち少なくともひとつの正方形には、
2本ダーツが当たっている。
１辺が10センチの正方形の中でもっとも離れている２点は、
対角に位置する頂点で、その距離は、10√2=14.142・・・センチ、すなわち１５センチ未満である。
同じ正方形内に２本ダーツが当たっているところでは、ダーツの距離は、１５センチ未満である。
解答・その12
（ペンネ−ム：夜ふかしのつらいおじさん）
●まず、1辺10の正方形にダーツは2本させないことを確認します。
1辺10の正方形の対角線は、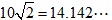
です。
いちばん離れていでも15にはなりません。
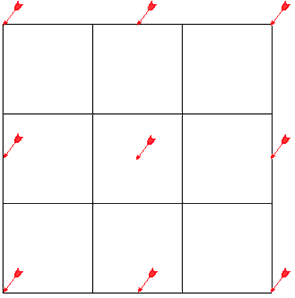●1辺30の正方形を1辺10の正方形に分割します。
この9個の正方形に1本ずつダーツをさします。
右のようにさすとどの2本も15以上離れます。
次の1本はどこかにさすことになります。
するとその小正方形の中では2本間の距離が15以下です。
解答・その13
（ペンネ−ム：杖のおじさん）
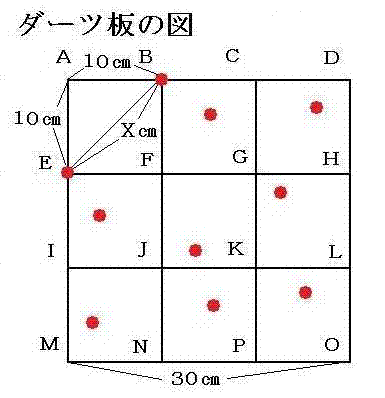
３０センチのダーツ板の縦と横に１０センチ幅の線を引きます。
ダーツは９つの枡のどこかに当る事になります。
一つの枡に２本当たると１５cm未満になることを証明いたします。
運悪く２本のダーツがその枡の角に当ったとしてもそのダーツ間の距離は１５cm未満になります。
最悪ダーツがＢとＥに当ったとします。対角線であるＢとＥの距離は１５ｃｍ未満であることは次の計算で分かります。
（線分ＡＢ）２＋（線分ＡＥ）２=（線分ＢＥ）２
Ｘ２＝１０２＋１０２＝２００
Ｘ＝√２００＝１４．１４２１４
従って。１５ｃｍ未満です。
解答・その14
（ペンネ−ム：オヤジ）
鳩ノ巣原理により証明する。
１辺３０センチの正方形ダーツ板を、１辺１０センチの正方形９個に分割する。
１辺１０センチの正方形９個 ・・・・これが鳩ノ巣
１０本のダーツ ・・・・・・・・・・これが鳩
従って９個の正方形の少なくとも１個には２本のダーツがささることになる、
よって、この２本のダーツは、距離が最大で対角線の長さの
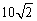センチ以下
すなわち１５センチ未満となる。
∴ 少なくとも２本のダーツの距離は１５センチ未満である。
解答・その15
（ペンネ−ム：MVH）
Adobe Systems1辺が30センチの正方形のダーツ板をTとします。
今、Tの1辺を3等分し、その辺と隣り合う辺も3等分します。
結局、Tは右図のように、9等分されます
（図のように、番号を振ります）。
さて、このダーツ板に10本のダーツを投げ、すべて板にささったとき、
そのうち、少なくとも2本は、同じ番号の領域にささります。
対称性により、ダーツ1とダーツ2が、同じ番号 (1) の領域にささった、
としても一般性を失いません。
この領域 (1) は、一辺10センチの正方形ですから、この正方形内の2点間の距離
が最も遠くなるのは、図のA、Bであり、その距離ABは、10×21/2 です。
今、10×21/2 ＜15 ⇔ 2×21/2 ＜3 ⇔ 8＜9 ですから、AB＜15 です。
従って、題意は示されました。（証終）■
〔解き終えて〕
問題文を読んですぐに、鳩ノ巣原理を思いつきました。問題文には「10」があります
から、「9」を作り出せば良いですね。鳩ノ巣原理は、小学生にも理解できる原理で
すが、その威力たるや、ものすごいですね。
正解者
| スモークマン | teki | オヤジ |
| のっこん | 転位反応 | 杖のおじさん |
| ＣＨ４ | ちょろんは太太 | Ryu1128 |
| 夜ふかしのつらいおじさん | 迷子の雄猫 | |
| もげぴ | MVH | 三角定規 |
コメント
この問題の解答で、気をつけなければならないのは、
どんな場合でも、「少なくとも２本のダーツの距離は15センチ未満」
であることを証明しなければならないことですね。
MVHさんのご指摘にもあるように、
こういう場面で鳩ノ巣原理(例えば、６羽の鳩が、５つの巣の中にいるとすると、
少なくとも１つの巣には、２羽以上の鳩がいる。）は大変、有効ですね。
top