栤戣174丂棫曽懱偵愽傓惓懡妏宍
棫曽懱傪侾偮偺暯柺偱愗抐偡傞偲偒丄昞柺偵愗傝岥偲偟偰偱偒傞惓懡妏宍偲偟偰
壜擻側傕偺傪偡傋偰摎偊偰偔偩偝偄丅
栤戣偺弌揟
夝摎
夝摎丒偦偺1
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
丒惓嶰妏宍偼偡偖偱偒傑偡偹丅
丒惓曽宍傕柧傜偐丅
丒惓榋妏宍傕奺曈偺拞揰傪寢傫偱峴偗偽壜擻丅
暯柺偱偼嵟崅偱俇杮偺曈偟偐愗傟側偄...曈偲柺偱偱偒傞偺偼1揰偩偗偩偐傜...崅乆俇妏宍傑偱...
丒偱偼丄惓屲妏宍偼壜擻偐丠
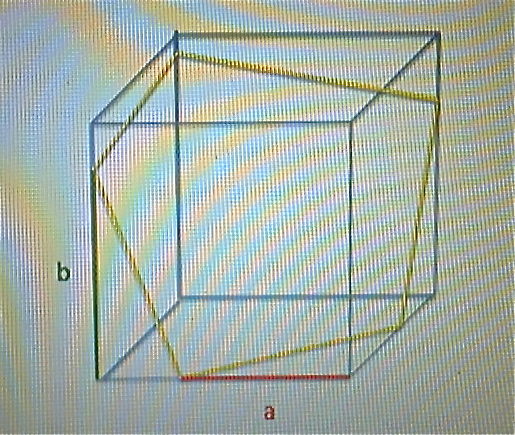
揧晅恾偺傛偆偵壜擻 !!
2a2=(1-a)2+b2
偙傟偑丄曈偺挿偝1埲忋偱偁傟偽傕偆侾揰偑庢傟傞...
2a2亞1
a亞併2/2
b2=a2+2a-1=(a+1)2-2亞(併2/2+1)2-2=併2-1亝1
偱丄恾宍揑偵偁傝摼傞偙偲偑傢偐傞 ^^
偗偭偒傚偔...
惓3乣6妏宍傑偱壜擻 ^^
Junko
惓屲妏宍偼丄俆曈偺挿偝偑摍偟偔丄偐偮撪妏傕摍偟偔側偗傟偽側傝傑偣傫偑丄
偙偺揰偼偄偐偑偱偟傚偆偐丅
偦偭偐...妏傕摍偟偔側傜側偒傖偄偗側偄傫偩...^^;
嵟屻偺妏偼柧傜偐偵90亱枹枮偵側偭偪傖偆偐傜...180*3/5=108亱傪枮偨偝側偄偐傜...嶌傟側偄偭偰...偦傫側偵娙扨偵尵偊傞偺偩傠偆偐...^^;...?
偦偆側傞偺偼...椉椬偺揰偐傜偼...忋偺埵抲偵偁傞偼偢側偺偱=椉椬偺揰傪尒壓傠偡偙偲偵側傞偺偱...90亱埲忋偵偼側傟側偄偙偲偑傢偐傞偱偄偄偺偐側偀...?
夝摎丒偦偺2
乮儁儞僱亅儉丗傕偘傄乯
摎
惓嶰妏宍丆惓曽宍媦傃惓榋妏宍
棟桼
師偺侾側偄偟俁偺偲偍傝丅
(杮摉側傜丆惓屲妏宍偑偱偒側偄偙偲丆惓幍妏宍埲忋偺惓懡妏宍偑偱偒側偄偙偲傕愢柧偡傋偒偲巚偄傑偡偑丆
帪娫愗傟偲側傝傑偟偨丅)
侾丂惓嶰妏宍
丂丂徹柧傪徣棯偟偰傕嫋偟偰偄偨偩偗傞偲巚偄傑偡丅
堦偮偺捀揰傪峔惉偡傞俁柺偺惓曽宍偺懳妏慄偱峔惉偝傟傞嶰妏宍偼丆偦偺奺曈偺挿偝偑摍偟偄偨傔惓嶰妏
宍偲側傝傑偡丅
俀丂惓曽宍
丂丂偁傞柺偲悈暯偵僇僢僩偡傞偲丆偦偺抐柺偼惓曽宍偲側傝傑偡丅
 俁丂惓俇妏宍
俁丂惓俇妏宍
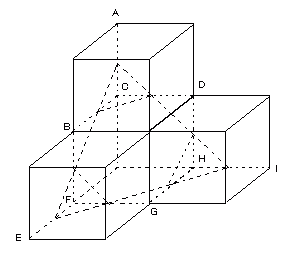
丂丂偒傟偄側恾偠傖側偔偰嫲弅偱偡偑丆棫曽懱係屄傪恾偺傛偆偵愊傒忋偘傞丅
曈俙俠丆曈俤俥丆曈俫俬偺拞揰乮愢柧偺曋媂忋丆捀揰偺堦晹偵偮偄偰俙側偄偟俥
偲柦柤乯傪寢傇偲 惓嶰妏宍偵側傝丆偙偙偐傜丆俙俠丆
俛俠丆俠俢偺奺曈偺拞揰傪寢傫偱偱偒傞惓嶰妏宍丆俛俥丆俤俥丆俥俧偺奺曈偺拞揰傪寢傫偱偱偒傞惓嶰妏宍丆俢俫丆俧俫丆俫俬偺奺曈偺拞揰傪寢傫偱偱偒傞惓
嶰妏宍傪愗傝庢傞偲巆偭偨榋妏宍偺奺捀揰偺妏搙偼偄偢傟傕侾俀侽搙(180-60)偱偁傝丆傑偨丆偦偺榋妏宍偺奺曈偺挿偝偼摍偟偄乮偄偢傟傕惓曽宍偺係
曈偺拞揰傪寢傫偱偱偒傞惓曽宍偺侾曈偲摍偟偄挿偝乯丅傛偭偰丆偙偺榋妏宍偼惓榋妏宍丅
夝摎丒偦偺3
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂丂惓嶰妏宍丄惓巐妏宍丄惓榋妏宍偺嶰庬椶偲側傝傑偡丅
棫曽懱傪愗偭偨帪偺惓懡妏宍偵偮偄偰挷傋傑偡丅
愗偭偨帪偵愙偡傞曈偼俁乣俇曈偲側傝傑偡丅
廬偭偰丄弌棃傞懡妏宍偼嶰妏宍乣榋妏宍偵側傝傑偡丅
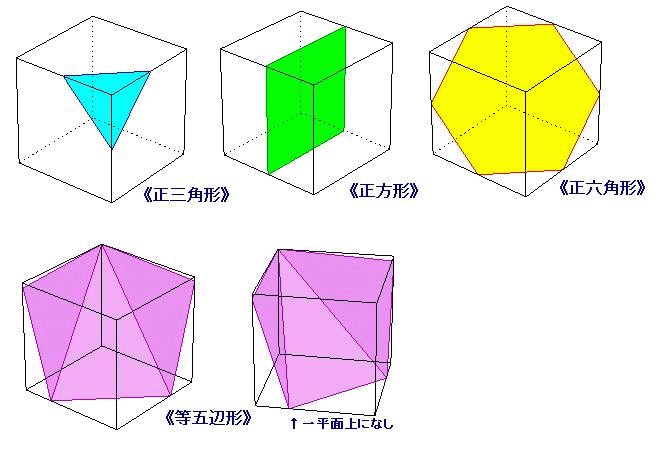
惓嶰妏宍丄惓巐妏宍丄惓榋妏宍偼壓恾偺傛偆偵側傝傑偡丅
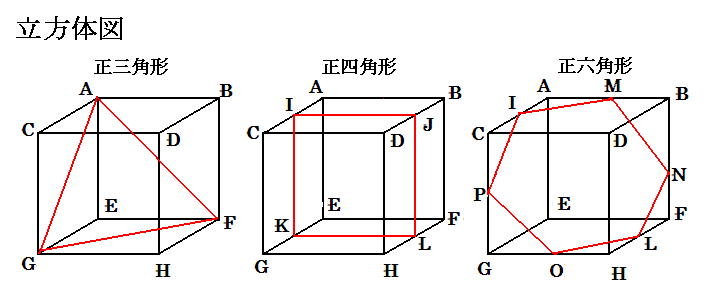
棫曽懱乮俙丆俛丆俠丆俢丆俤丆俥乯偺愢柧
揰丂俬丆俲丆俴丆俰丆俵丆俹丆俷丆偼奺曈偺拞揰偲偟傑偡丅奺曈偺挿偝傪倃偲偟傑偡丅
(1)丂恾偺惓嶰妏宍俙丆俧丆俫偺奺曈偺挿偝偼併俀亊倃偲側傝傑偡丅
嶰妏宍偺愗傝曽偼曈俢俠丆俢俛丆俢俫丆偺曈忋偺俢偐傜摨偠挿偝偺揰傪捠傞傛偆偵愗偭偰傕惓嶰妏宍偵側傝傑偡丅
(2) 惓巐妏宍丂恾偱偼俬丆俰丆俲丆俴偱偡偑奺棫曽懱偺暯柺偵悅捈偐暯峴偵愗抐偡傟偽丄
惓巐妏宍偵側傝傑偡丅奺曈偺挿偝偼倃偲側傝傑偡丅
(3)丂惓榋妏宍俬丆俹丆O丆俴丆俶丆俵丂偱丂惓榋妏宍偺奺曈偺挿偝偼併俀/俀亊倃偲側傞丅
屲妏宍偼俆曈傪捠傟偽弌棃傑偡偑丄惓屲妏宍偼弌棃傑偣傫丅
夝摎丒偦偺4
乮儁儞僱亅儉丗teki乯
摎偊丂丂惓嶰妏宍丄惓曽宍丄惓榋妏宍
棫曽懱偵偼丄柺偑俇柺偁傝傑偡丅
棟榑揑偵偼丄惓嶰妏宍偐傜惓榋妏宍偺係庬椶偑偱偒傞壜擻惈偑偁傞傫偱偡偑丄
惓屲妏宍偼偳偆愗抐偟偰傕嶌傟傑偣傫丅
惓嶰妏宍偼丄棫曽懱偺妏傪摍嫍棧偵愗傝棊偲偣偽偱偒傑偡丅
惓曽宍偼丄棫曽懱偺柺偲暯峴側柺偱愗抐偡傟偽偱偒傑偡丅
惓榋妏宍偑偪傚偭偲暋嶨偱偡偑丄棫曽懱偺忋柺偺妏傪嫴傓俀曈偺拞揰傪寢傫偩慄暘偲
壓柺偺懳妏傪嫴傓俀曈偺拞揰傪寢傇慄暘傪娷傓暯柺偱愗抐偡傟偽丄偙偺愗抐柺偼惓
榋妏宍偲側傝傑偡丅
側偍丄捠忢偺俆妏宍偼偱偒傞傫偱偡偑丄惓屲妏宍偼偳偺傛偆側愗抐柺偱愗抐偟偰傕
晄壜擻偱偡丅
夝摎丒偦偺5
乮儁儞僱亅儉丗haya乯
棫曽懱傪堦偮偺暯柺偱愗抐偡傞偲偒偵尰傟傞惓懡妏宍偺抐柺宍忬偼丄
惓嶰妏宍丒惓曽宍丒惓榋妏宍偺俁偮偱偁傞丅
亂夝偒曽亃
惓嶰妏宍偼Fig.1偺傛偆偵3偮偺捀揰傪娷傓暯柺偱愗抐偡傞偐丄偙傟偲暯峴側暯柺偱壜擻丅
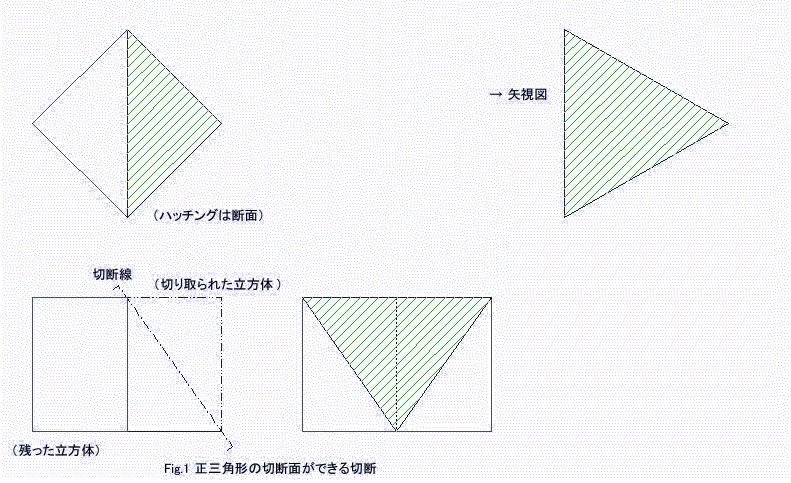
惓曽宍偼Fig.2偺傛偆偵暯峴側4曈偺拞揰傪捠傞暯柺偐丄偙傟偲暯峴側暯柺偱壜擻丅
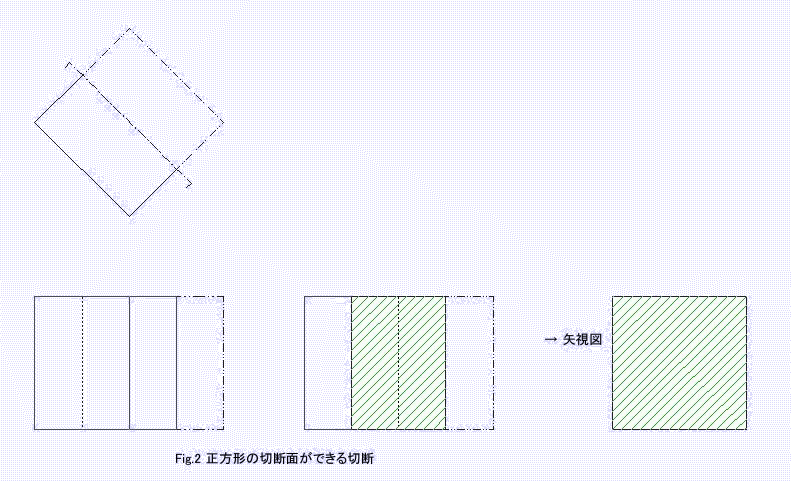
惓榋妏宍Fig.3偺傛偆偵6曈偺拞揰傪捠傞暯柺偱愗抐偡傞偙偲偵傛偭偰壜擻丅
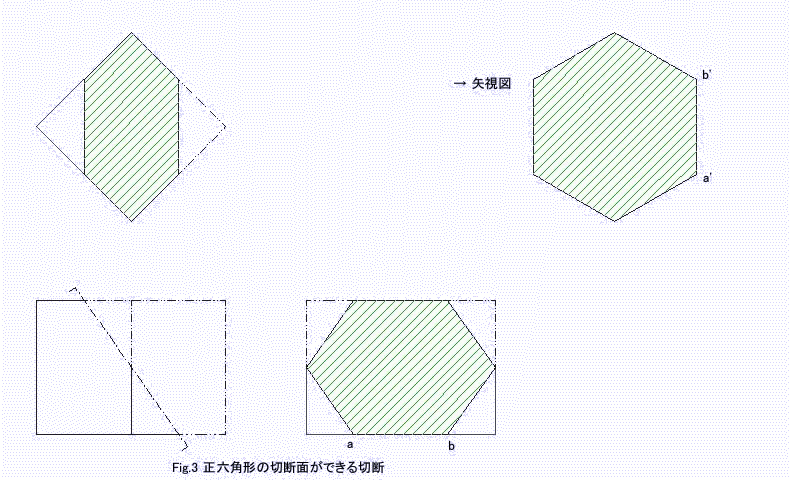
幍妏宍埲忋偼棫曽懱偑6柺懱偱偁傞偙偲偐傜偱偒側偄丅
傑偨丄惓屲妏宍傕偱偒側偄丅
屲妏宍偺抐柺偼Fig.3偺擇揰 a, b 傪 X-Y 幉忋偺 c 偵摑崌偡傟偽嶌恾壜擻偱偁傞偑丄宍惉偝傟傞
捀妏 c' 偼90亱傛傝戝偒偔偱偒側偄丅丂惓屲妏宍偺捀妏偼慡偰108亱偱偁傞偙偲傛傝惓屲妏宍偼偱偒側偄丅
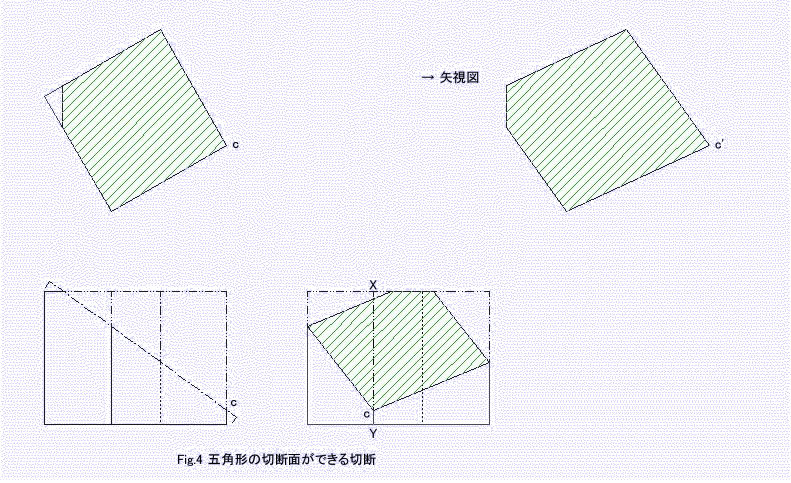
夝摎丒偦偺6
乮儁儞僱亅儉丗僆儎僕乯
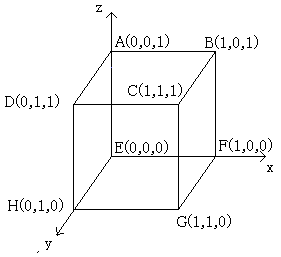
棫曽懱偺堦曈傪侾偵偟偰丂棫曽懱俙俛俠俢亅俤俥俧俫偵捈岎嵗昗傪偄傟傞丅
俙乮侽丆侽丆侾乯丂俛乮侾丆侽丆侾乯丂俠乮侾丆侾丆侾乯丂俢乮侽丆侾丆侾乯
俤乮侽丆侽丆侽乯丂俥乮侾丆侽丆侽乯丂俧乮侾丆侾丆侽乯丂俫乮侽丆侾丆侽乯偲偡傞偲
椺偊偽丂仮俙俥俫丗堦曈偺惓嶰妏宍偲側傞丅
椺偊偽丂棫曽懱偺奺柺偵暯峴側暯柺偱愗傞偲堦曈侾偺惓曽宍偲側傞丅
椺偊偽丂俙俢偺拞揰丄俙俛偺拞揰丄俛俥偺拞揰丄俥俧偺拞揰丄俧俫偺拞揰丄
俫俢偺拞揰傪捠傞暯柺偱愗傞偲堦曈 侾/併2丂偺惓榋妏宍偲側傞丅
偙偙偱丄惓屲妏宍偑弌棃側偄偐峫嶡偡傞丅堦曈 倎 偲偡傞偲

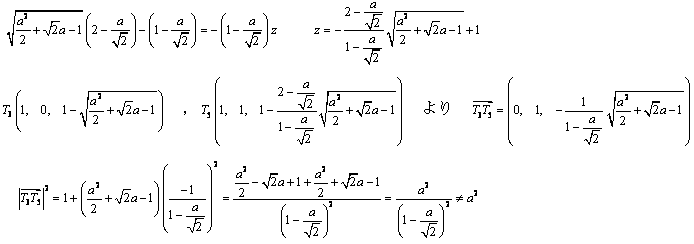
廬偭偰惓屲妏宍偲側傜側偄丅
惓榋妏宍埲忋偺惓懡妏宍偼丄弌棃側偄偺偱
丂亪丂惓嶰妏宍丆惓曽宍丄惓榋妏宍
夝摎丒偦偺7
乮儁儞僱亅儉丗嶰妏掕婯乯
棫曽懱偺暯柺偵傛傞愗抐柺偲偟偰尰傟傞傕偺偼丆
丂丒惓嶰妏宍 乧 傂偲偮偺捀揰偐傜摍嫍棧偵偁傞俁曈忋偺俁揰傪捠傞暯柺偱愗抐偡傞
丂丒惓曽宍丂 乧 傂偲偮偺柺偵暯峴側暯柺偱愗抐偡傞
丂丒惓榋妏宍 乧 俇曈偺拞揰傪捠傞暯柺偱愗抐偡傞
偺俁偮乻恾乼(by Grapes3D)丅
惓屲妏宍偼偱偒側偄傕偺偐偲偄傠偄傠寁嶼偟丆摍屲曈宍傑偱偼峴偒拝偄偨偺偱偡偑丆巆擮側偑傜偙偺屲曈宍偼堦暯柺忋偵偁傝傑偣傫偱偟偨丅
惓屲妏宍偍傛傃惓幍妏宍埲忋偼丆僉僠儞偲徹柧偱偒偨傢偗偱偼偁傝傑偣傫偑丆柍棟側偺偱偼側偄偱偟傚偆偐丅
夝摎丒偦偺8
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
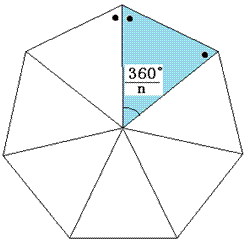 仠惓n妏宍偺1偮偺撪妏偺戝偒偝偼丄
仠惓n妏宍偺1偮偺撪妏偺戝偒偝偼丄
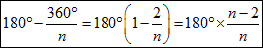
側偺偱丄師偺傛偆偵側傝傑偡丅
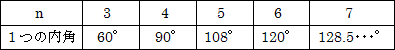
仠棫曽懱傪1偮偺暯柺偱愗傞偲偒丄
惓嶰妏宍丄惓曽宍丄乮惓榋妏宍乯偑偱偒傞偺偼偡偖偵傢偐傝傑偡丅
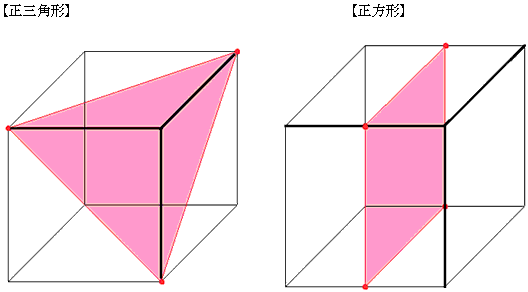
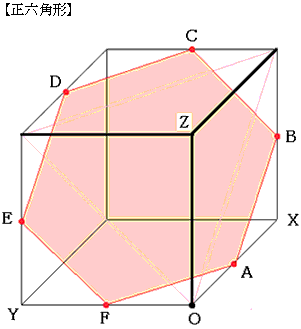
惓嶰妏宍偲惓曽宍偼栤戣側偄偲巚偄傑偡丅
惓榋妏宍偼恾偱奺曈偺拞揰傪寢傫偩傕偺偱偡丅
仠擮偺偨傔恾宍ABCDEF偑惓榋妏宍偱偁傞偙偲傪妋偐傔傑偡丅
懳徧惈偐傜奺曈偺挿偝丄撪妏偑摍偟偄偙偲偼傢偐傝傑偡丅
揰A丄B丄C丄D丄E丄F偑摨堦暯柺忋偵偁傞偙偲傪挷傋傑偡丅
忋偺恾偺傛偆偵丄堦曈偺挿偝偑1偺棫曽懱傪偍偒傑偡丅
奺揰偺嵗昗傪師偺傛偆偵偲傝傑偡丅

偙偺幃偼丄揰C丄D丄E偺嵗昗傪戙擖偟偰傕惉棫偡傞偺偱丄揰A丄B丄C丄D丄E丄F偼摨堦暯柺忋偵偁傝傑偡丅
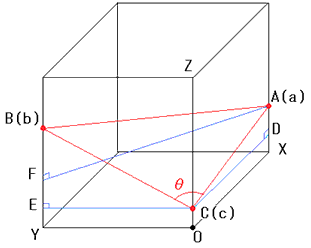 仠栤戣偼丄惓屲妏宍傗惓幍妏宍埲忋偑偱偒側偄偙偲偱偡丅
仠栤戣偼丄惓屲妏宍傗惓幍妏宍埲忋偑偱偒側偄偙偲偱偡丅
惓屲妏宍埲忋偼丄堦偮偺撪妏偑撦妏乮捈妏傛傝戝乯偱偡
恾偺傛偆偵堦曈偺挿偝1偺棫曽懱傪偍偒傑偡丅
揰A丄B丄C偺嵗昗偼Z嵗昗偲偟傑偡丅
乮 c亝倎亝倐丂偲偟傑偡乯
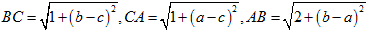
傛傝丄
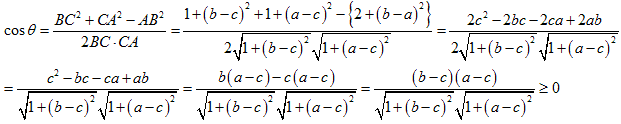
偲側傞偺偱丄兤偼撦妏偵偼側傝傑偣傫丅
乮cos兤偺抣偑晧偺偲偒偵丄撦妏偵側傝傑偡丅
c=a 傑偨偼丄c=b 偺偲偒丄cos兤=0 偲側傝丄兤亖90亱偲側傝傑偡乯
偮傑傝丄暯柺偑3偮偺暯峴側曈傪墶愗傞傛偆側応崌偼惓屲妏宍埲忋偵偼側傝傑偣傫丅
乮椺偊偽丄c=0 偺偲偒丄5妏宍偵側傞偙偲偼偁傝傑偡偑丄惓屲妏宍偵偼側傝傑偣傫乯
暯柺偑暯峴側3偮偺暯峴側曈傪墶愗傜側偄傛偆側応崌偼丄6妏宍偑偱偒傑偡丅
5妏宍偲7妏宍埲忋偼偱偒傑偣傫丅
仠埲忋偐傜偱偒傞偺偼丄惓嶰妏宍丄惓曽宍丄惓榋妏宍偱偡丅
夝摎丒偦偺9
乮儁儞僱亅儉丗揮埵斀墳乯
棫曽懱傪侾偮偺暯柺偱愗抐偡傞偲偒丄棫曽懱偺傂偲偮偺柺偵懳偟偰嵟戝偱侾偮偺曈偑宍惉偝傟傞偺偱丄
惓懡妏宍偺曈偺悢偼嵟戝偱俇偑峫偊傜傟傞丅傑偨丄暯柺傪宍惉偡傞偵偼彮側偔偲傕俁曈偑昁梫偱偁傞丅
埲忋傛傝丄惓懡妏宍偺壜擻惈偲偟偰偼丄惓嶰妏宍丄惓曽宍丄惓屲妏宍丄惓榋妏宍偱偁傞丅
惓嶰妏宍丄惓曽宍丄惓榋妏宍偵偮偄偰偼丄埲壓偺恾偺捠傝丅
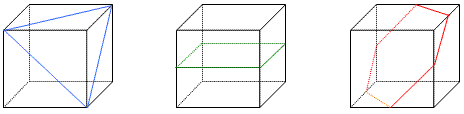
偝偰丄惓屲妏宍偵偮偄偰専徹傪峴偆丅
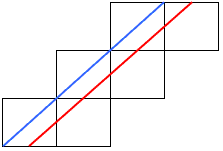
棫曽懱偺揥奐恾偲惓嶰妏宍媦傃惓榋妏宍偺愗抐慄傪埲壓偵帵偟偨丅
惓嶰妏宍偲惓榋妏宍偺応崌偵偼丄偦傟偧傟嶰偮偺柺丄榋偮偺柺傪愗抐偡傞挿偝傪摨偠偵偱偒傞偑丄
摨條側曽朄偱屲偮偺柺傪愗抐偡傞慄傪堷偔偙偲偼偱偒側偄丅
傛偭偰丄惓屲妏宍偼宍惉偱偒側偄丅
夝摎丒偦偺10
乮儁儞僱亅儉丗T_Tatekawa乯
傑偢丆棫曽懱偺柺偼6偮側偺偱丆暯柺偱愗抐偡傞尷傝偵偍偄偰偼
6偮偺曈傑偱偟偐抐柺偵娷傓帠偑弌棃偢丆幍妏宍埲忋偼偱偒側偄丏
棫曽懱偺捀揰偺堦偮傪尨揰偵庢傝丆偦偙偐傜怢傃傞曈傪偦傟偧傟
x幉丆y幉丆z幉偵廳偹偰嵗昗傪偲傞丏
1. 惓嶰妏宍
椺偊偽 (1, 0, 0), (0, 1, 0), (0, 0, 1) 傪捠傞暯柺偱愗抐偡傞丏
2. 惓曽宍
xy 暯柺丆yz 暯柺丆 zx 暯柺偵暯峴側暯柺偱愗抐偡傞丏
3. 惓榋妏宍
(0.5, 0, 0), (0, 0.5, 0), (1, 0, 0.5), (0, 1, 0.5),
(0.5, 1, 1), (1, 0.5, 1) 傪捠傞暯柺偱愗抐偡傞丏
巐妏宍埲忋偺抐柺傪庢傠偆偲偡傞偲丆棫曽懱偺4偮埲忋偺柺偵愗傝岥偑
擖傞丏
棫曽懱偼岦偐偄崌偆柺偑暯峴側偺偱丆愗傝岥偺懡妏宍偼巐妏宍
埲忋偺応崌偼丆昁偢暯峴側堦懳埲忋偺曈偑懚嵼偡傞丏
堦曽偱惓屲妏宍偵偼暯峴側曈偑側偄丏偙偺偨傔丆棫曽懱偺抐柺偱
惓屲妏宍傪嶌傞帠偼弌棃側偄丏
傛偭偰惓嶰妏宍丆惓曽宍丆惓榋妏宍偺嶰偮偑摼傜傟傞丏
夝摎丒偦偺11
乮儁儞僱亅儉丗偺偭偙傫乯
堦曈偺挿偝偑俀偺棫曽懱偱峫偊傞
A(-1,1,1),B(-1,-1,1),C(1,-1,1),D(1,1,1),
E(-1,1,-1),F(-1,-1,-1),G(1,-1,-1),H(1,1,-1)偲偡傞
侾乯惓嶰妏宍偑偱偒傞偐偳偆偐専摙偡傞
EF忋偺揰乮F傪娷傓乯傪P丄EH忋偺揰乮H傪娷傓乯傪Q偲偟偨帪
A丄P丄Q傪捠傞暯柺偱愗抐偡傞偲嶰妏宍偑偱偒傞
AF=AH=FH=2併2偩偐傜
A丄F丄H傪捠傞暯柺偱愗抐偡傞偲堦曈偺挿偝偑2併2偺惓嶰妏宍偑偱偒傞
俀乯惓巐妏宍偑偱偒傞偐偳偆偐専摙偡傞
暯柺ABCD偁傞偄偼暯柺CGHD偁傞偄偼暯柺DHEA偵暯峴側暯柺偱愗抐偡傞偲
堦曈偺挿偝偑2偺惓巐妏宍偑偱偒傞
俁乯惓屲妏宍偑偱偒傞偐偳偆偐専摙偡傞
FG忋偺揰傪P丄HG忋偺揰傪Q偲偟偨帪
A丄P丄俻傪捠傞暯柺偱愗抐偡傞偲屲妏宍偑偱偒傞
偙偺帪丄愗抐柺偲BF偺岎揰傪R丄愗抐柺偲DH偺岎揰傪S偲偡傞
暯柺AEFB偲暯柺CGHD偼暯峴偩偐傜AR偲SQ偼暯峴
暯柺BFGC偲暯柺DHEA偼暯峴偩偐傜RP偲AS偼暯峴
俀慻偺曈偑暯峴偱偁傞屲妏宍ARPQS偼惓屲妏宍偵偼側傝偊側偄
乮惓屲妏宍偼偳偺俀曈傪偲偭偰傕暯峴偱偼側偄乯
係乯惓榋妏宍偑偱偒傞偐偳偆偐専摙偡傞
AB忋偺揰傪P丄AD忋偺揰傪Q丄FG忋偺揰傪R偲偟偨帪
P丄Q丄R傪捠傞暯柺偱愗抐偡傞偲榋妏宍偑偱偒傞
AB偺拞揰傪S丄AD偺拞揰傪T丄FG偺拞揰傪U偲偟
S丄T丄U傪捠傞暯柺偱愗抐偡傞偲
堦曈偺挿偝偑併2偺惓榋妏宍偑偱偒傞
棫曽懱傪侾偮偺暯柺偱愗抐偡傞帪偵俈屄埲忋偺岎揰偑偱偒傞偙偲偼側偄偐傜
愗傝岥偲偟偰壜擻側懡妏宍偼惓嶰妏宍丄惓巐妏宍丄惓榋妏宍偺俁庬椶偑偡傋偰偱偁傞
惓屲妏宍偑晄壜擻偱偁傞偙偲偺榑徹偵嬯楯偟傑偟偨
崱寧傕傑偨乽扨弮側偺偵傓偢偐偟偄乿偄偄栤戣偱偟偨
夝摎丒偦偺12
乮儁儞僱亅儉丗Ryu1128乯
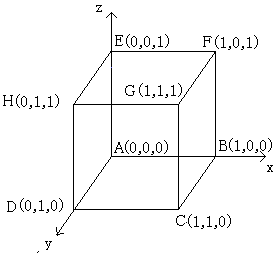
- 棫曽懱偼丄惓榋柺懱偱偡丅
- 暯柺偲暯柺偺岎嵎偼捈慄乮慄暘乯偵側傝傑偡丅
- 傛偭偰丄擟堄偺暯柺偲壓婰慄暘曽掱幃偲偺岎嵎晹偼慄暘偵側傞偐夝柍偟偲側傝傑偡丅
棫曽懱傪丄俙(0,0,0)傪尨揰偲偟偰奺乆偺捀揰傪(x,y,z)偺棫懱嵗昗偱昞尰偟傑偡丅
俛(1,0,0)丂俠(1,1,0)丂俢(0,1,0)丂俤(0,0,1)丂俥(1,0,1)丂G(1,1,1)丂H(0,0,1)
棫曽懱偺奺曈偺曽掱幃偼師偺傛偆偵12偺慄暘曽掱幃側傝傑偡
忋偐傜弴斣偵(1)乣(12)偲偟傑偡丅
擟堄偺暯柺曽掱幃傪師偺傛偆偵偍偒傑偡丅
丂丂倎倶+倐倷+們倸-倓亖0丒丒丒(13)
偆傑偔擟堄偺暯柺傪12曈偲岎嵎偝偣偰岎嵎偟偨慄暘偺挿偝偑慡偰堦抳偟妿偮丄擟堄偺暯柺忬偵偍偗傞偲側傝偁偆慄暘偺岎嵎妏搙偑慡偰堦抳偡傞偲惓12妏宍偑弌棃傑偡丅偟偐偟側偑傜捀柺偐傜乮偳偺柺偐傜愗偭偰傕傛偄偺偱偡偑乯擖傞偲偟偰丄棫曽懱偺愗傜傟傞曈乮枖偼捀揰乯偼嵟戝俇偱偡丅
偦偺棟桼偼慡偰偺柺乮俇柺乯傪愗偭偨応崌懡妏宍偺捀揰偼俇偵側傞偐傜偱偡丅
愗傜傟偨抜柺偼昁偢偦偺捀揰偑椉椬偺柺偲嫟桳偡傞偙偲偵側傝傑偡丅偦偟偰暯柺偱愗傞偨傔棫曽懱偺堦偮偺柺傪愗傞応崌嵟戝偱傕2曈偟偐愗傞偙偲偑偱偒傑偣傫丅
棫曽懱偼6柺偱偁傝偦偺慡偰偺柺傪愗偭偨応崌6亊2曈亐2乮嫟桳乯偱捀揰悢偼6偲側傝傑偡丅
惓懡妏宍偺掕媊偺媍榑偼旔偗偰捠傞偨傔偵惓2妏宍偼峫偊傑偣傫丒丒丒丅
愭偢惓嶰妏宍偐傜
偙傟偼丄擟堄偺暯柺偑倶丄倷丄倸幉忋偺摨偠抣倠乮扐偟倠亜0丄倠亙亖3乯
傪捠傞傛偆偵偡傟偽椙偄傢偗乮懠偵傕棫曽懱偺奺捀揰偐傜摨偠抣傪偲傞偙偲傕乯偱偡偐傜壜擻偱偡丅
場傒偵暯柺曽掱幃偺夝偺堦偮偼丄
倶+倷+倸亖倠2丅懠偵傕夝偼俛俠俢偐傜摍嫍棧傪庢傞偲3庬椶偁傝傑偡丅
偮偓偵惓曽宍偱偡偑彴丄壆崻暻偵暯峴側暯柺偱愗傞偲慡偰惓曽宍偵側傝傑偡丅
偦偺懠丄x2+y2=1丄y2+倸2=1丄
x2+倸2=1偲(13)偺楢棫偱昞偝傟傞暯柺孮傕棫曽懱傪惓曽宍偵愗傝傑偡丅
惓5妏宍傪旘偽偟偰惓6妏宍傪峫偊傑偡丅
慜弎偟偨偲偍傝6柺傪慡偰愗傞暯柺傪峫偊傑偡丅彴偐傜擖偭偰丄4暻傪捠傝丄壆崻傊敳偗傞暯柺傪峫偊傑偡丅
偙偺偲偒彴偲壆崻傪愗傞曈媦傃懳柺偡傞暻傪愗傞曈偼暯峴偵側傝傑偡丅
俙俛丄俛俥丄俥俧丄俧俫丄俫俢丄俢俙忋偵揰倠1乣倠6傪庢傝傑偡丅
暯柺(13)偑倠1乣倠6傪慡偰捠傝丄
倠i倠i+1亖倠i+1倠i+2乮倝亖1乣4乯乻奺曈偑摍偟偄乼
妿偮倠i倠i+3亖倠i+1倠i+4丂乮倝亖1乣2乯乻懳妏慄偑摍偟偄乼偑尵偊傟偽惓6妏宍偑弌棃傑偡丅
棫曽懱偺奺曈乮俙俛丄俛俥丄俥俧丄俧俫丄俫俢丄俢俙乯偺拞揰偵倠1乣倠6
傪庢傞偲忋婰忦審傪慡偰枮偨偟傑偡丅
傛偭偰惓6妏宍偼壜擻偱偡丅
嵟屻偵旘偽偟偨惓5妏宍偱偡偑丄5妏宍偼6妏宍偵愗傞応崌偺堦柺偵偍偄偰棫曽懱偺曈傪愗傜偢偵捀揰傪愗傞偙偲偵傛偭偰偺傒壜擻偱偡丅
6妏宍偱専摙偟偨捠傝丄捀揰偺懳曈埲奜偺椬傝崌傢側偄曈偼昁偢暯峴偲側偭偰偟傑偆偨傔惓屲妏宍偵愗傞偺偼晄壜擻偱偡丅
偙偺偙偲偼丄暻偵暯峴偱側偄偳傫側暯柺偱愗偭偰傕愗傜傟偨暻偼暯峴偵側偭偰偟傑偆偙偲偐傜柧傜偐偱偡丅
夝摎丒偦偺13
乮儁儞僱亅儉丗偪傚傠傫偼懢懢乯
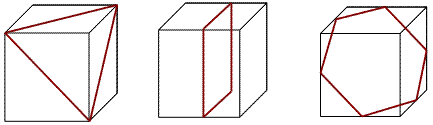
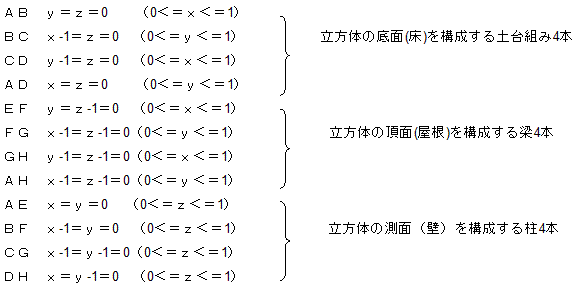
棫曽懱偼丄柺偑6枃偱偁傞偺偱丄1暯柺偲岎傢偭偰偱偒傞捈慄偼6杮傑偱丅
愗傝岥偵嶌傜傟傞懡妏宍偼丄嶰妏宍丄巐妏宍丄屲妏宍丄榋妏宍偩偗偱丄偦傟傛傝戝偒偄傕偺偼丄偱偒側偄丅
忋恾偺傛偆偵丄惓嶰妏宍偼丄俁捀揰傪捠傞柺偱愗傟偽嶌傜傟傞丅
惓巐妏宍偼丄係曈偺拞揰傪捠傞柺偱偒傟偽傛偄丅
惓榋妏宍傕丄恾偺傛偆偵丄俇曈偺拞揰傪捠傞柺偱愗傟偽丄嶌傞偙偲偑偱偒傞丅
傑偨丄暯峴偟偰偄傞俀枃偺柺偲暯柺偑岎傢偭偨応崌丄偦傟偧傟偺柺偲岎傢偭偨偲偙傠偵偱偒傞捈慄偼丄
屳偄偵暯峴偵側傞丅
棫曽懱偼丄俁慻偺俀枃偺暯峴柺偱嶌傜傟偰偄傞丅偙傟傪峫椂偡傞偲丄愗傝岥偵偱偒傞俆妏宍偵偼丄
俀慻偺暯峴慄偑側偗傟偽側傜側偄丅
惓屲妏宍偺奺曈偼暯峴偱偼側偄偺偱丄愗傝岥偵惓屲妏宍傪嶌傞偙偲偼偱偒側偄丅
傛偭偰丄摎偊偼丄惓嶰妏宍丄惓巐妏宍丄惓榋妏宍偺俁庬椶偱偁傞丅
夝摎丒偦偺14
乮儁儞僱亅儉丗MVH乯
寢榑偐傜弎傋傑偡.
棫曽懱傪1偮偺暯柺偱愗抐偡傞偲偒, 昞柺偵愗傝岥偲偟偰偱偒傞惓懡妏宍偲偟偰壜擻側傕偺偼, 埲壓偱慡偰偱偡.
乽惓嶰妏宍, 惓曽宍乮惓巐妏宍乯, 惓榋妏宍乿
鶣乯傑偢偼, 偙偺3偮偑幚尰壜擻偱偁傞偙偲傪帵偟傑偡.
棫曽懱偺俉捀揰傪, (亇1,亇1,亇1)乮暋崋擟堄乯偲偟傑偡乮偙偺偲偒, 棫曽懱偺堦曈偺挿偝偼2偲側傝傑偡乯.
惓嶰妏宍丗3揰(亅1,亅1,1),(1,亅1,亅1),(1,1,1)傪捠傞暯柺x亅y+z亅1=0丗偱愗抐偡傞偲, 愗傝岥偼惓嶰妏宍偵側傝傑偡.
惓曽宍丗3揰(0,亅1,1),(0,1,1),(0,1,亅1)傪捠傞暯柺丗x=0偱愗抐偡傞偲, 愗傝岥偼惓曽宍偵側傝傑偡.
惓榋妏宍丗3揰(亅1,0,1),(0,1,1),(1,1,0)傪捠傞暯柺x亅y+z=0丗偱愗抐偡傞偲, 愗傝岥偼惓榋妏宍偵側傝傑偡.
鶤乯師偵, 愗傝岥偑惓屲妏宍偵偼側傜側偄偙偲傪帵偟傑偡.
師偺2偮乽暯峴偱側偄2偮偺暯柺偑岎傢傞偲捈慄偑偱偒傞乿,
乽棫曽懱偺岦偐偄崌偆柺偼暯峴偱偁傞乿偼徹柧側偟偵擣傔傞偙偲偵偟傑偡.
傑偨, 棫曽懱偺曈偵増偭偨暯柺偱愗抐偡傞応崌, 愗傝岥偼挿曽宍偵偟偐側傜側偄偺偱,
偙偺応崌傪彍奜偟偰峫偊傑偡. 曗戣傪2偮梡堄偟傑偡.
曗戣1丗棫曽懱偺1偮偺柺偵偼, 愗傝岥偺屲妏宍偺1偮偺曈偟偐尰傟側偄.
乮徹柧乯1偮偺柺偵愗傝岥偺屲妏宍偺2偮埲忋偺曈偑尰傟傞偲壖掕偡傞偲,
忋婰偱擣傔偨偙偲偵柕弬偟傑偡. 仩
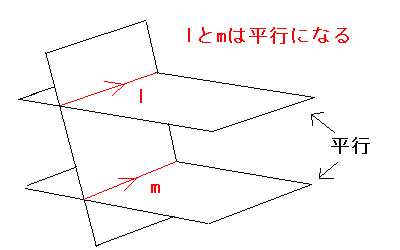
曗戣2丗暯峴側2暯柺P, Q偵1偮偺暯柺R偑岎傢偭偰偱偒傞2偮偺捈慄倢, 倣偼暯峴偱偁傞.
乮徹柧乯P偲Q偼暯峴側偺偱, 偦偺堦晹偱偁傞倢偲倣偑岎傢傞偙偲偼偁傝摼傑偣傫.
傑偨, 倢偲倣偼椉曽偲傕R忋偺捈慄側偺偱, 偹偠傟偺埵抲偵偼偁傝傑偣傫. 傛偭偰, 倢偲倣偼暯峴偱偡.
偝偰, 徹柧偵擖傝傑偡.
棫曽懱傪暯柺偱愗抐偟屲妏宍傪偮偔傞偲, 偦偺曈偼, 曗戣侾偵傛傝棫曽懱偺5偮偺柺偵1偮偢偮尰傟傑偡. 堦曽, 棫曽懱偺俇偮偺柺偼2偮偢偮偑暯峴偱偡偐傜, 愗傝岥偺5偮偺曈偺偆偪, 偆傑偄2曈偺慻崌偣傪峫偊傞偲, 偦傟傜偼暯峴側2偮偺柺偵偦傟偧傟尰傟偰偄傞偙偲偵側傝傑偡. 曗戣2偵傛傝, 偙偺傛偆偵偟偰尒偮偗偨2偮偺曈偼昁偢暯峴偵側傞偙偲偑暘偐傝傑偡. 傛偭偰, 棫曽懱傪暯柺偱愗抐偟偰嶌偭偨屲妏宍偼, 暯峴側2偮偺曈傪娷傓宍偵偟偐側傝傑偣傫. 偲偙傠偑, 惓屲妏宍偺曈偼偳偺2杮傕暯峴偱偼側偄偱偡偐傜, 惓屲妏宍傪嶌傞偙偲偼偱偒傑偣傫. 仩
鶥乯愗傝岥偑幍妏宍埲忋偵偼側傜側偄偙偲傪帵偟傑偡.
乮徹柧乯棫曽懱偑6柺偱偁傞偙偲偲曗戣侾乮偵憡摉偡傞媍榑乯偵傛傝帺柧偱偡丅仩
埲忋鶣乯乣鶥乯偵傛傝, 朻摢偺寢榑傪摼傑偡. 仭
乲夝偒廔偊偰乴
戣嵽偲偟偰偼拞妛惗曈傝偑懳徾偱偟傚偆偑, 惓屲妏宍偑壗屘嶌傟側偄偺偐, 偲偄偆栤偄偼,
側偐側偐嫽枴怺偄傕偺偱偟偨.
夝摎丒偦偺15(捛壛 9/11)
乮儁儞僱亅儉丗塝壀乯
乵夝摎乶 惓嶰妏宍丄惓曽宍丄惓榋妏宍
乵峫偊曽乶
忋婰偺惓嶰妏宍埲奜偼曈偺挿偝偱偼側偔丄曈偺埵抲娭學傪峫椂偡傟偽傛偄丅
棫曽懱傪侾偮偺暯柺偱愗抐偟偨偲偒偵愗傝岥偲偟偰偱偒傞懡妏宍傪峫偊傞偵偁偨傝丄
師偺侾亱偲俀亱傪峫椂偡傟偽廫暘偱偁傞丅
侾亱 曈偼棫曽懱偺柺忋偵偁傝丄偄偢傟偺柺傕偦偺忋偵偁傞曈偼崅乆侾偮偱偁傞丅
俀亱 棫曽懱偺懳柺忋偵俀偮偺曈偑偁傟偽丄偦傟傜偼暯峴偱偁傞丅
侾亱傛傝丄愗傝岥偲偟偰偱偒傞懡妏宍偼崅乆俇偮偺曈偱偁傞偐傜丄
嶰妏宍丄巐妏宍丄屲妏宍丄榋妏宍偵尷傜傟傞乮幍妏宍埲忋偼偱偒側偄乯丅
俀亱傛傝丄惓屲妏宍偼暯峴側曈傪傕偨側偄偺偱偱偒側偄丅
乵俀亱偺曗懌乶
暯峴側俀偮偺暯柺傪暿偺暯柺偱愗抐偟偨偲偒偵偱偒傞愗傝岥偼丄俀偮偺暯峴側捈慄偵側傞丅
惓夝幰
| teki | 偪傚傠傫偼懢懢 | 僗儌乕僋儅儞 |
| T_Tatekawa | 偺偭偙傫 | 揮埵斀墳 |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | Ryu1128 | haya |
| 僆儎僕 | 忨偺偍偠偝傫 | 嶰妏掕婯 |
| MVH | 傕偘傄 |
僐儊儞僩
栤戣偼僔儞僾儖偱偡偑丄惓屲妏宍偑側偤偱偒側偄偐傪帵偡偲側傞偲丄 偪傚偭偲峫偊偰偟傑偄傑偡偹丅
 top
top