栤戣173丂儅僗栚忋偺巐妏宍
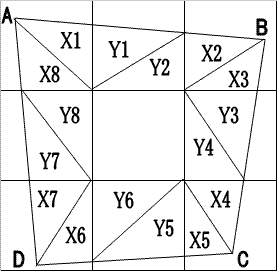
堦曈侾偺惓曽宍俋偮偐傜側傞丄俁峴俁楍偺儅僗栚傪峫偊傑偡丅
奺儅僗栚偵偼丄壓恾偺傛偆偵斣崋傪偮偗傑偡丅

俙丆俛丆俠丆俢偼偦傟偧傟惓曽宍丂(1)丆(3)丆(5)丆(7)丂偺撪晹乮嫬奅偼娷傑側偄乯偺揰偲偟傑偡丅
巐妏宍俙俛俠俢偲惓曽宍丂(1)丆(3)丆(5)丆(7)丂偲偺嫟捠晹暘偺柺愊偺榓傪倃偲偍偒丄
巐妏宍俙俛俠俢偲惓曽宍丂(2)丆(4)丆(6)丆(8)丂偲偺嫟捠晹暘偺柺愊偺榓傪倄偲偍偔偲偒丄
倃亙倄偑惉傝棫偮偙偲傪徹柧偟偰偔偩偝偄丅
栤戣偺弌揟
僕儏僯傾悢妛僆儕儞僺僢僋 2003-2008
悢妛僆儕儞僺僢僋嵿抍丂曇
夝摎
夝摎丒偦偺1
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
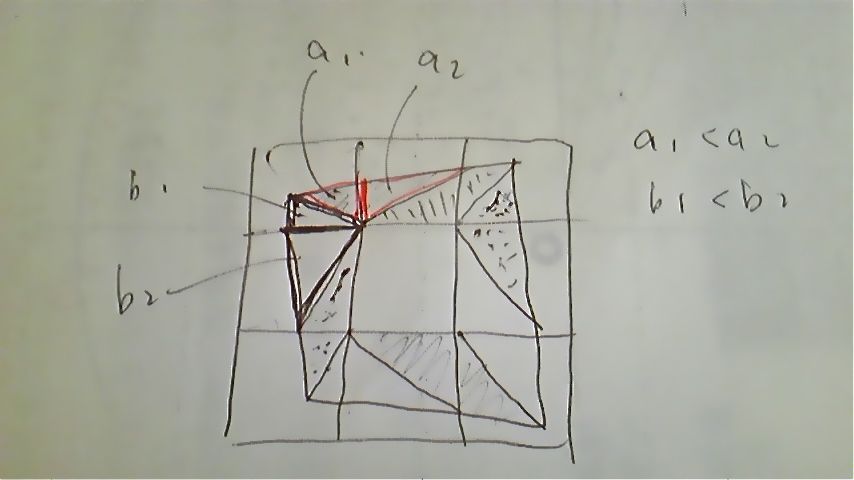
揧晅恾尒傟偽柧傜偐側偺偱偡偑...
傛偆偼丄妏偺晹暘傛傝丄忢偵拞娫偺晹暘偺柺愊偑戝偒偄偐傜偭偰偙偲偵側傞偐傜偱偡傛偹丅
妏偺晹暘偼椬摨巑偺晹暘偲掙曈偑摨偠嶰妏宍偵暘夝偱偒丄拞娫晹暘偺仮偼崅偝偑彫惓
曽宍偺侾曈暘側偺偱丄忢偵妏偺晹暘偺仮偼戝偒偔側傟側偄偺偱 !!
夝摎丒偦偺2
乮儁儞僱亅儉丗偪傚傠傫偼懢懢乯
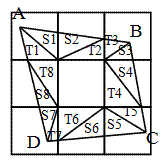 巐妏宍ABCD偲丄乮侾乯丄乮俀乯丄丒丒丒丄乮俉乯偺廳側偭偨偲偙傠偵偱偒偨巐妏宍偺偦傟偧傟傪恾偺傛偆偵
懳妏慄偱擇偮偺嶰妏宍偵傢偗丄偦傟偧傟偺嶰妏宍偺柺愊傪S1丄T1丄S2丄T2丄丒丒丒丄S8丄T8偲偡傞丅
巐妏宍ABCD偲丄乮侾乯丄乮俀乯丄丒丒丒丄乮俉乯偺廳側偭偨偲偙傠偵偱偒偨巐妏宍偺偦傟偧傟傪恾偺傛偆偵
懳妏慄偱擇偮偺嶰妏宍偵傢偗丄偦傟偧傟偺嶰妏宍偺柺愊傪S1丄T1丄S2丄T2丄丒丒丒丄S8丄T8偲偡傞丅
S1偲S2傪斾妑偡傞偲丄掙曈偼嫟捠丅S2偺崅偝偼丄彫惓曽宍偺堦曈偺挿偝偱偁傞偑丄
S1偺崅偝偼惓曽宍偺堦曈傛傝抁偄丅丂亪丂S1亙S2
摨條偵峫偊偰丄丂T3亙T2丄S3亙S4丄T5亙T4丄S5亙S6丄T7亙T6丄S7亙S8丄T1亙T8
備偊偵丄S1+T3+S3+T5+S5+T7+S7+T1亙S2+T2+S4+T4+S6+T6+S8+T8
忋幃偺嵍曈偼 X丄塃曈偼 Y偱偁傞偐傜丄X亙Y丂丒丒丒丂乮廔乯
夝摎丒偦偺3
乮儁儞僱亅儉丗儅僔儍乯
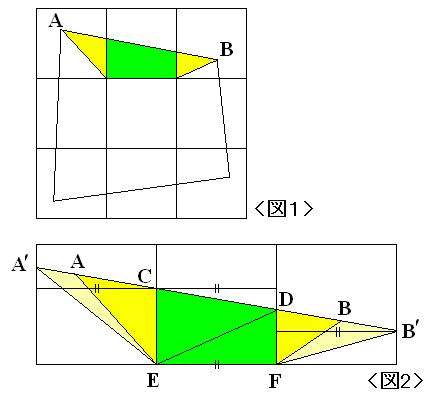
9偮偺惓曽宍偺偆偪斣崋偑晅偗傜傟偰偄側偄惓曽宍偺揰傪偦傟偧傟丄a,b,c,d偲偍偔丅
偝傜偵AB傪寢傫偩偲偒偵惓曽宍偺曈偲偺岎揰傪a',b'偲偍偔丅
偙偺偲偒嶰妏宍Aaa' 偲嶰妏宍Bbb' 偺榓偑巐妏宍 aa'b'b傛傝彫偝偄偙偲偑徹柧偱偒傟偽
摨條偵懠偺嶰妏宍偲巐妏宍偺娭學偑帵偣傞偺偱X亙Y偑帵偣傞丅
嶰妏宍Aaa'偲嶰妏宍aa'b偵拲栚偡傞丅
偙偺偲偒aa'傪掙曈偲尒側偣偽丄柺愊偺戝彫偼崅偝偱寛傑傞丅
揰A偼(1)偺撪晹偺揰偱偁傞偺偱丄嶰妏宍Aaa'偺崅偝偼1枹枮偱偁傞丅
堦曽嶰妏宍aa'b偺崅偝偼曈ab側偺偱1偱偁傞丅
備偊偵嶰妏宍Aaa'亙嶰妏宍aa'b偱偁傞丅
摨條偵偟偰嶰妏宍Bbb''亙嶰妏宍bb'a'偱偁傞丅
埲忋偐傜嶰妏宍Aaa' 偲嶰妏宍Bbb' 偺榓偑巐妏宍 aa'b'b傛傝彫偝偄偙偲偑徹柧偝傟偨丅
摨條偵懠偺嶰妏宍偲巐妏宍偺娭學偑帵偣傞偺偱X亙Y偑徹柧偝傟偨丅
夝摎丒偦偺4
乮儁儞僱亅儉丗Ryu1128乯
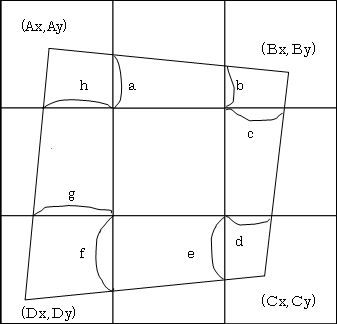 俙偺椞堟偵懏偡傞柺愊偺偆偪俙偺尨揰偲俙媦傃巐妏宍偲乮1乯乮2乯偺嫬奅偺岎揰偑嶌
傞嶰妏宍偺柺愊偼丂倎丒俙倶/2丂丂乮慄傪堷偗側偐偭偨偺偱偔偳偔側傝傑偟偨乯
俙偺椞堟偵懏偡傞柺愊偺偆偪俙偺尨揰偲俙媦傃巐妏宍偲乮1乯乮2乯偺嫬奅偺岎揰偑嶌
傞嶰妏宍偺柺愊偼丂倎丒俙倶/2丂丂乮慄傪堷偗側偐偭偨偺偱偔偳偔側傝傑偟偨乯
摨條偵俛椞堟偺摨偠嶰妏宍偺柺愊偼倐丒俛倶/2
乮2乯偵懏偡傞戜宍偺柺愊偼乮倎+倐乯丒侾/2丂忋婰乮1乯偲乮3乯偵懏偡傞嶰妏宍偺柺愊偺榓偲斾妑偡傞偲
丂丂倎丒俙倶/2丂+丂倐丒俛倶/2丂亙倎丒1/2丂+丂倐丒1/2丂乮俙倶亙1丄俛倶亙1偐傜乯摨條偵
丂丂們丒俛倷/2丂+丂倓丒俠倷/2丂亙們丒1/2丂+丂倓丒1/2丂
丂丂倕丒俠倶/2丂+丂倖丒俢倶/2丂亙倕丒1/2丂+丂倖丒1/2丂
丂丂倗丒俢倷/2丂+丂倛丒俙倷/2丂亙倗丒1/2丂+丂倛丒1/2
晄摍幃偺曅乆懌偡偲嵍曈偼乮1乯乮3乯乮5乯乮7乯偵懏偡傞柺愑亖倃偲側傝
塃曈偼乮2乯乮4乯乮6乯乮8乯亖倄偲側傞偺偱
倃亙倄偑惉傝棫偪傑偡丅
夝摎丒偦偺5
乮儁儞僱亅儉丗偺偭偙傫乯
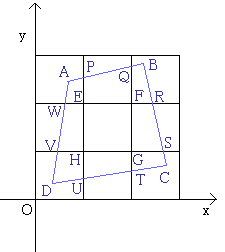 惓曽宍乮俈乯偺壓偺曈傪x幉丄惓曽宍乮俈乯偺嵍偺曈傪y幉偲偡傞
惓曽宍乮俈乯偺壓偺曈傪x幉丄惓曽宍乮俈乯偺嵍偺曈傪y幉偲偡傞
捈慄AB偲x=1偲偺岎揰傪P丄捈慄AB偲x=2偲偺岎揰傪Q丄揰(1,2)傪E丄揰(2,2)傪F偲偡傞
PE=a,QF=b,A偲PE偲偺嫍棧傪們,B偲QF偲偺嫍棧傪d偲偡傞偲
丂丂乮a,b,c,d偼偄偢傟傕0傛傝戝偒偔1傛傝彫偝偄乯
乮戜宍PEFQ)丒2=a+b
乮仮AEP+仮BQF乯丒2=ac+bd
a+b-(ac+bd)=a(1-c)+b(1-d)亜0
傛偭偰
丂乮仮AEP+仮BQF乯亙乮戜宍PEFQ乯丒丒丒丒丒丒(1)
捈慄BC偲y=2偲偺岎揰傪R丄捈慄BC偲y=1偲偺岎揰傪S丄揰(2,1)傪俧偲偡傞偲摨條偵偟偰
丂乮仮BFR+仮CSG乯亙乮戜宍FGSR乯丒丒丒丒丒丒(2)
捈慄CD偲x=2偲偺岎揰傪T丄捈慄CD偲x=1偲偺岎揰傪U丄揰(1,1)傪俫偲偡傞偲摨條偵偟偰
丂乮仮CGT+仮DUH乯亙乮戜宍HUTG乯丒丒丒丒丒丒(3)
捈慄DA偲y=1偲偺岎揰傪V丄捈慄DA偲y=2偲偺岎揰傪W偲偡傞偲摨條偵偟偰
丂乮仮DHV+仮AWE乯亙乮戜宍WVHE乯丒丒丒丒丒丒(4)
(1)丄(2)丄(3)丄(4)傪曈乆壛偊偰丂X亙Y
夝摎丒偦偺6
乮儁儞僱亅儉丗haya乯
巐妏宍俙俛俠俢偲惓曽宍丂(1)丆(3)丆(5)丆(7)丂偲偺嫟捠晹暘偺柺愊偺榓傪倃偲偍偒丄
巐妏宍俙俛俠俢偲惓曽宍丂(2)丆(4)丆(6)丆(8)丂偲偺嫟捠晹暘偺柺愊偺榓傪倄偲偍偔偲偒丄倃亙倄偑惉傝棫偮
亂夝偒曽亃
拞怱偺彫惓曽宍偺捀揰偐傜曗彆慄傪堷偔偙偲偵傛傝栤戣偺椞堟傪壓偺恾偺擛偔4暘妱偡傞丅
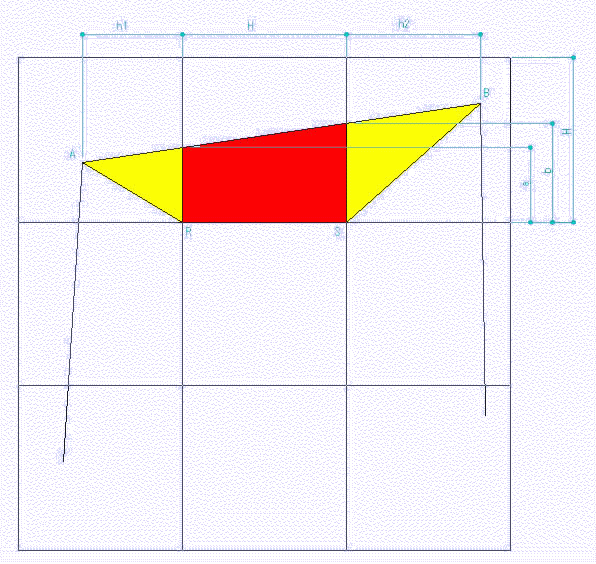
偦偺撪丄(1)-(2)-(3)偵娭傢傞忋懁偺晹暘丄偮傑傝巐曈宍 A-B-S-R 偵偮偄偰専摙偡傞丅
X偵懏偡傞柺愊偼墿怓丄 Y偵懏偡傞柺愊偼愒丄彫惓曽宍偺堦曈偺挿偝傪H偲偟偨丅
丂丂X = (a*h1)/2 + (b*h2)/2
丂丂Y = (a+b)H/2
A,B偼彫惓曽宍偺撪晹偺揰偱偁傞偐傜柧傜偐偵丄
丂丂h1 亙 H
丂丂h2 亙 H
傛傝丄
丂丂X 亙 Y
懠偺3偮偺椞堟偵偮偄偰傕摨偠偙偲偑尵偊傞丄傛偭偰戣堄偺擛偟丅
夝摎丒偦偺7
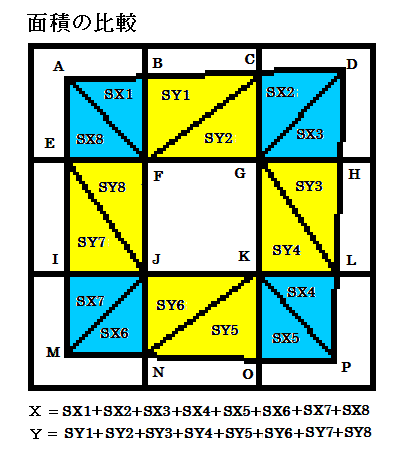
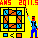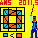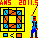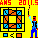 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
壓恾傪嶲徠
丂丂倃亖俽倃侾亄丒丒丒丒丒丒亄俽倃俉
丂丂倄亖俽倄侾+丒丒丒丒丒丒亄俽倄俉
仮俽倃侾偲仮俽倄侾偺柺愊偼仮俽倄侾偺曽偑戝偒偄徹柧
仮俽倃侾偺崅偝曈俙俛偼儅僗栚偺暆枹枮丄仮俽倄侾偺崅偝曈俛俠偼儅僗栚偺暆偱偡丅
掙曈俛俥偼嫟捠偱偡丅
廬偭偰丄乮掙曈亊崅偝乯亐俀偺岞幃偵婎偯偄偰寁嶼偡傞偲俽倃侾亙俽倄侾偲側傝傑偡丅
仮俽倃俀偲仮俽倄俀偺柺愊偼仮俽倄俀偺曽偑戝偒偄徹柧
仮俽倃俀偺崅偝俠俢偼儅僗栚偺暆枹枮丄仮俽倄俀偺崅偝曈俛俠偼儅僗栚偺暆偱偡丅
掙曈俛俧偼嫟捠偱偡丅
廬偭偰丄乮掙曈亊崅偝乯亐俀偺岞幃偵婎偯偄偰寁嶼偡傞偲俽倃俀亙俽倄俀偲側傝傑偡丅
偙偺傛偆偵俽倃侾偐傜俽倃俉傑偱峫偊偰偄偔偲丄
丂丂俽倃侾亄丒丒丒丒丒丒亄俽倃俉亖倃亙倄亖俽倄侾+丒丒丒丒丒丒亄俽倄俉
偱偁傞偙偲偑徹柧弌棃傑偡丅
夝摎丒偦偺8
乮儁儞僱亅儉丗柪巕偺梇擫乯
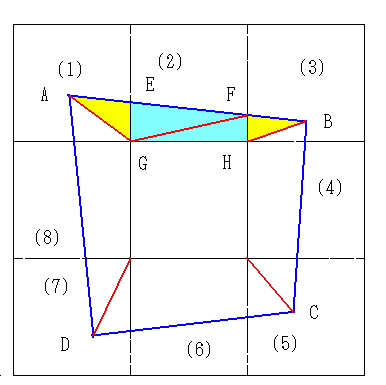 恾偺捠傝奺揰偵柤慜傪偮偗傞丅
恾偺捠傝奺揰偵柤慜傪偮偗傞丅
巐妏宍ABCD偺奺捀揰偲拞墰偺儅僗栚偲傪寢傇丅
嶰妏宍AEG偲嶰妏宍EFG偼掙曈偑摨偠側偺偱丄崅偝偺掅偄嶰妏宍AEG偺傎偆偑柺愊偼嫹偄丅
嶰妏宍BFH偲嶰妏宍FGH偼掙曈偑摨偠側偺偱丄崅偝偺掅偄嶰妏宍BFH偺傎偆偑柺愊偼嫹偄丅
側偤側傜揰A,B偼儅僗栚偺撪晹偵偁傞偐傜丅
傛偭偰恾偺墿怓偺嶰妏宍偺柺愊偺榓偼丄恾偺悈怓偺巐妏宍偺柺愊傛傝嫹偄丅
惵怓偺巐妏宍偺慡偰偺曈偵偮偄偰摨條偺徹柧偑惉傝棫偮偺偱丄恾偲忋婰偺徹柧偐傜丄惓曽宍丂(1)丆(3)丆(5)丆(7)丂偲偺嫟捠晹暘偼惓曽宍丂(2)丆(4)丆(6)丆(8)丂偲偺嫟捠晹暘傛傝傕柺愊偼嫹偄丅
傛偭偰倃亙倄偑惉傝棫偮丅
夝摎丒偦偺9
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
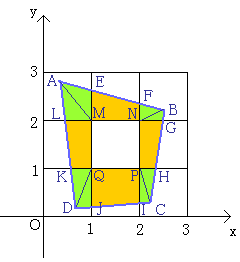
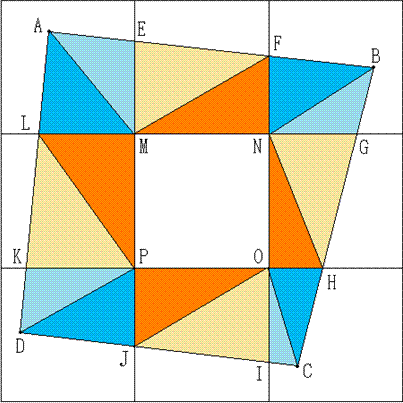 恾偺傛偆偵曗彆慄傪堷偒丄X偲Y偺椞堟偵偁傞巐妏宍傪嶰妏宍偵暘妱偟傑偡丅
恾偺傛偆偵曗彆慄傪堷偒丄X偲Y偺椞堟偵偁傞巐妏宍傪嶰妏宍偵暘妱偟傑偡丅
擹偄怓偲擹偄怓丄敄偄怓偲敄偄怓偺嶰妏宍偺柺愊傪斾妑偟傑偡丅
X偺椞堟偵偁傞嶰妏宍偼崅偝偑1傛傝彫偝偔丄Y偺椞堟偵偁傞嶰妏宍偼崅偝偑1偵偱偒傑偡丅
椺偊偽丄仮AEM偲仮MEF偲偱丄掙曈傪嫟捠偵EM偲偟傑偡丅
仮AEM偺崅偝偼揰A偑嫬奅忋偵側偄偙偲偐傜1傛傝彫偝偄偱偡丅
仮MEF偺崅偝偼揰F偑嫬奅忋側偺偱1偱偡丅
傛偭偰丄仮AEM亙仮MEF偱偡丅
偙偺傛偆偵峫偊偰丄
X亖仩AEML亄仩BGNF亄仩CIOH亄仩DKPJ
丂亖仮ALM亄仮AEM亄仮BFN亄仮BGN亄仮CHO亄仮CIO亄仮DJP亄仮DKP
丂亙仮PLM亄仮MEF亄仮MFN亄仮NGH亄仮NHO亄仮OIJ亄仮OJP亄仮PKL
丂亖仮MEF亄仮MFN亄仮NGH亄仮NHO亄仮OIJ亄仮OJP亄仮PKL亄仮PLM
丂亖仩EFNM亄仩GHON亄仩IJPO亄仩KLMN
丂亖Y
夝摎丒偦偺10
乮儁儞僱亅儉丗傕偘傄乯
 恾偺傛偆偵倃侾側偄偟倃俉丆倄侾側偄偟倄俉偺嶰妏宍偵暘妱偡傞丅
恾偺傛偆偵倃侾側偄偟倃俉丆倄侾側偄偟倄俉偺嶰妏宍偵暘妱偡傞丅
倃倎偲倄倎乮倎偼1側偄偟8偺擟堄偺惍悢乯偺嫬奅慄傪掙曈偲偡傞偲丆
倃倎偺崅偝偼侾枹枮丆倄倎偺崅偝偼侾側偺偱丆(倃倎偺柺愊)亙(倄倎偺柺愊)偲側傞丅
亪丂(倃侾側偄偟倃俉偺柺愊崌寁)亙(倄侾側偄偟倄俉偺柺愊崌寁)
亪丂倃亙倄
夝摎丒偦偺11
乮儁儞僱亅儉丗嶰妏掕婯乯
 戣堄傪帵偡偵偼丆亙恾侾亜偺 乽墿怓偺柺愊亙椢怓偺柺愊乿 乧 (*) 傪帵偣偽傛偄丅
戣堄傪帵偡偵偼丆亙恾侾亜偺 乽墿怓偺柺愊亙椢怓偺柺愊乿 乧 (*) 傪帵偣偽傛偄丅
奼戝恾亙恾俀亜偺傛偆偵丆奺揰傪掕傔傞丅偙偺偲偒丆
丂仮A'CE亖仮CDE丆仮B'DF亖仮DEF
偱偁傞偐傜丆
丂仮A'CE亄仮B'DF亖仮CDE亄仮DEF亖戜宍CDFE 乧(1)
柧傜偐偵 仮ACE亙仮A'CE丆仮BDF亙仮B'DF 乧(2)
偩偐傜丆(1)(2)傛傝
丂仮ACE亄仮BDF亙戜宍CDFE
埲忋偱 (*) 偑帵偝傟丆傛偭偰戣堄偼徹柧偝傟偨丅[椆]
夝摎丒偦偺12
乮儁儞僱亅儉丗MVH乯
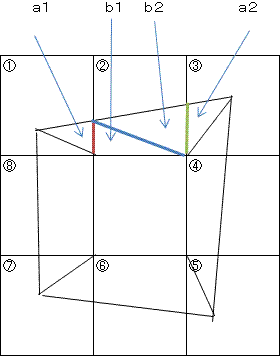
 梌偊傜傟偨3峴3楍偺儅僗栚傪, 儅僗栚乮俈乯偺嵍壓偺捀揰偑尨揰O偵, 乮侾乯乮俉乯
乮俈乯偺嵍懁偺奺曈偑y幉忋偵, 乮俈乯乮俇乯乮俆乯偺壓懁偺奺曈偑x幉忋偵偦傟偧傟
偔傞傛偆偵, 嵗昗暯柺偵抲偒傑偡.
梌偊傜傟偨3峴3楍偺儅僗栚傪, 儅僗栚乮俈乯偺嵍壓偺捀揰偑尨揰O偵, 乮侾乯乮俉乯
乮俈乯偺嵍懁偺奺曈偑y幉忋偵, 乮俈乯乮俇乯乮俆乯偺壓懁偺奺曈偑x幉忋偵偦傟偧傟
偔傞傛偆偵, 嵗昗暯柺偵抲偒傑偡.
偙偺偲偒, 巐妏宍ABCD偺曈AB偑x亖1, x亖2偲岎傢傞揰傪偦傟偧傟E, F, 曈BC偑倷亖
俀, y亖1偲岎傢傞揰傪偦傟偧傟G, H, 曈CD偑x亖2, x亖1偲岎傢傞揰傪偦傟偧傟I, J,
曈DA偑y亖1, y亖2偲岎傢傞揰傪偦傟偧傟K, L偲偟傑偡. 傑偨, 揰乮1丆2乯, 揰乮2丆
2乯, 揰乮2丆1乯, 揰乮1丆1乯傪偦傟偧傟M, N, P, Q偲偟傑偡.
傑偨, 仮AME偲仮BNF偺柺愊偺榓, 仮BNG偲仮CPH偺柺愊偺榓, 仮CPI偲仮DQJ偺柺愊偺
榓, 仮DQK偲仮AML偺柺愊偺榓傪偦傟偧傟A_1, A_2, A_3, A_4偲偍偒傑偡. 傑偨, 戜宍
MNFE, 戜宍NPHG, 戜宍PQJI, 戜宍QMLK偺柺愊傪偦傟偧傟B_1, B_2, B_3, B_4偲偍偒傑
偡. 偙傟傜偺戜宍偺崅偝偼, MN=NP=PQ=QM=1偱偡.
偝偰, 仮AME偵偍偄偰, 掙曈傪ME亖x偲尒偨偲偒偺崅偝傪a偲偟傑偡. 傑偨, 仮BNF偵偍
偄偰, 掙曈傪NF=y偲尒偨偲偒偺崅偝傪b偲偟傑偡.偙偺偲偒,
丂丂A_1亖(ax+by)/2, B_1=(x+y)/2
偱偡偐傜,
丂丂B_1亅A_1=(x+y亅ax亅by)/2=((1亅a)x+(1亅b)y)/2.
偙偙偱, 戣堄偵傛傝, 0亙a亙1, 0亙b亙1偱偡偐傜,
丂丂B_1亅A_1亜0, 偡側傢偪, A_1亙 B_1.
慡偔摨條偵偟偰, i=2, 3, 4偵懳偟偰傕,
丂丂A_i丂亙丂B_i
偑尵偊傑偡.廬偭偰,
丂丂A_1+A_2+A_3+A_4丂亙丂B_1+B_2+B_3+B_4,
偡側傢偪,
丂丂X亙Y
偑帵偝傟傑偟偨.
夝摎丒偦偺13
乮儁儞僱亅儉丗teki乯
 倎侾偺柺愊偼丄掙曈偑愒怓偺晹暘偱崅偝偑侾枹枮乮惓曽宍偺慄忋偵揰傪庢傟側偄偨傔乯丄
堦曽丄倐侾偺柺愊偼丄掙曈偑愒怓偺晹暘偱崅偝偼侾偱偡丅
倎侾偺柺愊偼丄掙曈偑愒怓偺晹暘偱崅偝偑侾枹枮乮惓曽宍偺慄忋偵揰傪庢傟側偄偨傔乯丄
堦曽丄倐侾偺柺愊偼丄掙曈偑愒怓偺晹暘偱崅偝偼侾偱偡丅
傛偭偰丄倐侾亜倎侾丅
摨條偵丄倎俀偺柺愊偼丄掙曈偑椢怓偺晹暘偱崅偝偑侾枹枮丄倐俀偺柺愊偼丄掙曈偑椢怓偺晹暘偱崅偝偼侾丅
傛偭偰丄倐俀亜倎俀丅
巆傝偺俁偮偺晹暘偵偮偄偰傕丄摨偠偙偲偑尵偊傞偺偱丄
嘇丄嘋丄嘐丄嘒偲偺嫟捠晹暘偺榓亖倄亜嘆丄嘊丄嘍丄嘑偲偺嫟捠晹暘偺榓亖倃丂丂偑尵偊傑偡丅
亙徹柧廔亜
夝摎丒偦偺14
乮儁儞僱亅儉丗T_Tatekawa乯
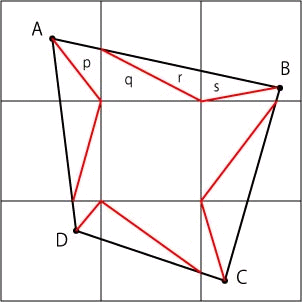 恾偺傛偆偵曗彆慄乮愒慄乯傪8杮堷偔丏
恾偺傛偆偵曗彆慄乮愒慄乯傪8杮堷偔丏
師偵曈AB偲拞怱偺彫惓曽宍偺捀揰偐傜側傞巐妏宍傪峫偊傞丏
偙偺巐妏宍偼嶰妏宍 p, q, r, s 偐傜惉傝棫偮丏
嶰妏宍 p, q 偼嫟捠偡傞曈傪帩偮丏
嶰妏宍 q 偼捈妏嶰妏宍偱丆柺愊偼
丂丂乮嫟捠偡傞曈偺挿偝乯亊乮彫惓曽宍偺1曈偺挿偝乯亐2
偱偁傞丏嶰妏宍 p 偺柺愊偼丆嶰妏宍偺亀崅偝亁偑彫惓曽宍偺1曈偺挿偝傛傝抁偄偺偱丆
丂丂乮嶰妏宍p偺柺愊乯亙乮嶰妏宍q偺柺愊乯
偱偁傞丏摨偠帠偑嶰妏宍 r, s 偵傕偄偊傞偺偱丆
丂丂乮嶰妏宍s偺柺愊乯亙乮嶰妏宍r偺柺愊乯
偲側傞丏椉曈傪懌偟偁傢偣傞偲丆
丂丂乮嶰妏宍p偺柺愊乯亄乮嶰妏宍s偺柺愊乯亙乮嶰妏宍q偺柺愊乯亄乮嶰妏宍r偺柺愊乯
偱偁傞丏曈BC丆CD丆DA傪娷傓巐妏宍偵偮偄偰摨條偵峫偊偰晄摍幃偺椉曈傪懌偟偁傢偣傞偲丆
丂丂X 亙 Y
偑惉傝棫偮丏
夝摎丒偦偺15
乮儁儞僱亅儉丗揮埵斀墳乯
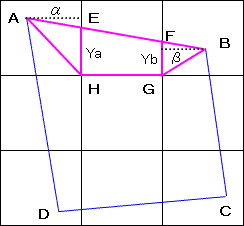 戣堄偺巐妏宍俙俛俠俢傪昤偒丄捀揰俙丄俛偐傜拞墰偺惓曽宍偺儅僗栚偺
捀揰俫丄俧傊捈慄傪堷偄偰丄巐妏宍俙俛俧俫偲偡傞丅
戣堄偺巐妏宍俙俛俠俢傪昤偒丄捀揰俙丄俛偐傜拞墰偺惓曽宍偺儅僗栚偺
捀揰俫丄俧傊捈慄傪堷偄偰丄巐妏宍俙俛俧俫偲偡傞丅
峏偵丄曈俙俛偲惓曽宍偺儅僗栚偲偺岎揰傪俤丄俥偲偡傞丅
偝偰丄倃亙倄偑惉傝棫偮偙偲傪徹柧偡傞偵偼丄
巐妏宍俙俛俧俫偵偍偄偰丄
嶰妏宍俙俤俫偺柺愊亄嶰妏宍俛俧俥偺柺愊亙戜宍俤俥俧俫偺柺愊
傪帵偣偽椙偄丅
(佹巐妏宍俙俛俠俢偺巆傝偺晹暘偵偮偄偰傕摨偠徹柧傪揥奐偱偒傞)
嶰妏宍俙俤俫偵偍偄偰丄掙曈傪俤俫丄偦偺挿偝傪Ya丄崅偝傪兛偲偡傞丅
摨條偵丄嶰妏宍俛俧俥偵偍偄偰丄掙曈傪俥俧丄偦偺挿偝傪Yb丄崅偝傪兝偲偡傞丅
戜宍俤俥俧俫偺柺愊亅乮嶰妏宍俙俤俫偺柺愊亄嶰妏宍俛俧俥偺柺愊乯
=(Ya+Yb)乛俀亅Ya丒兛乛俀亅Yb丒兝乛俀
=乷Ya乮1-兛乯亄Yb乮1亅兝乯乸乛俀丂亜侽
乮佹戣堄傛傝丄侽亙兛亙侾丄侽亙兝亙侾乯
亪 倄-倃亜侽
亪 倃亙倄
惓夝幰
| 栭傆偐偟偺偮傜偄偍偠偝傫 | 儅僔儍 | 揮埵斀墳 |
| 偪傚傠傫偼懢懢 | haya | 偺偭偙傫 |
| teki | 柪巕偺梇擫 | T_Tatekawa |
| MVH | 忨偺偍偠偝傫 | Ryu1128 |
| 傕偘傄 | 僗儌乕僋儅儞 | 嶰妏掕婯 |
僐儊儞僩
奆偝傫偐傜偍婑偣偄偨偩偄偨夝摎偵偁傞傛偆偵丄恾宍傪嶰妏宍偵暘妱偟偰峫偊傞偲偄偄偱偡偹丅
懡偔偺曽偑嶌恾傕偟偰偄偨偩偒丄姶幱偄偨偟傑偡丅
 top
top