Challenge!

問題171　３桁の数の問題

１．正整数ｎに対して、ｎを十進表示したときの各桁の数字の和をａ(ｎ)で表す。

　　　ａ(１)＋ａ(２)＋・・・＋ａ(９９９)

を求めよ。

２．正整数ｎに対して、ｎを十進表示したときの０でない各桁の数字の積をｂ(ｎ)で表す。

　　　ｂ(１)＋ｂ(２)＋・・・＋ｂ(９９９)

を求めよ。

---

問題の出典

ジュニア数学オリンピック 2003-2008
数学オリンピック財団　編

解答

解答・その1

（ペンネ−ム：浜田　明巳）

エクセルのマクロで解きました。問題１は，13500．問題２は，97335です．

  Option Explicit
Sub Macro1()
    Sheets("Sheet1").Select
    Dim a(999) As Integer
    Dim b(999) As Integer
    Dim n As Integer
    For n = 1 To 999
      Cells(n, 1).Value = aa(n)
      Cells(n, 3).Value = bb(n)
      Range("A" & n).Select
    Next n
    Cells(1, 2).Value = "=SUM(A1:A999)"
    Cells(1, 4).Value = "=SUM(C1:C999)"
    Range("B1").Select
End Sub
Private Function aa(ByVal n As Integer) As Integer
    aa = n Mod 10
    aa = aa + ((n \ 10) Mod 10)
    aa = aa + n \ 100
End Function
Private Function bb(ByVal n As Integer) As Integer
    Dim b0 As Integer
    b0 = n Mod 10
    If b0 > 0 Then
      bb = b0
    Else
      bb = 1
    End If
    b0 = (n \ 10) Mod 10
    If b0 > 0 Then
      bb = bb * b0
    End If
    b0 = n \ 100
    If b0 > 0 Then
      bb = bb * b0
    End If
End Function

---

解答・その2

（ペンネ−ム：エルドス）

答えは（１） 13500 （２） 97335
１０進ＢＡＳＩＣで組みました。いい練習問題だと思います。

CLEAR
DIM a(1000),b(1000)
FOR n=1 TO 999
   LET n2=INT(n/100)
   LET n1=INT(MOD(n,100)/10)
   LET n0=INT(MOD(n,10)/1) 
   LET a(n)=n2+n1+n0
   LET sa=sa+a(n)
   LET b(n)=1
   IF n2>0 THEN LET b(n)=b(n)*n2
   IF n1>0 THEN LET b(n)=b(n)*n1
   IF n0>0 THEN LET b(n)=b(n)*n0
   LET sb=sb+b(n)
   rem   PRINT n,a(n),b(n)
NEXT n
PRINT "sa=";sa,"sb=";sb
END
  実行結果
sa= 13500               sb= 97335 

---

解答・その3

（ペンネ−ム：杖のおじさん）

答え、問題１、１３５００、問題２、９７３３５

各列（各桁）に１から９までの数字が１００個あることが分かります。

問題１
３×（９×１０/２）×１００＝１３５００

問題２
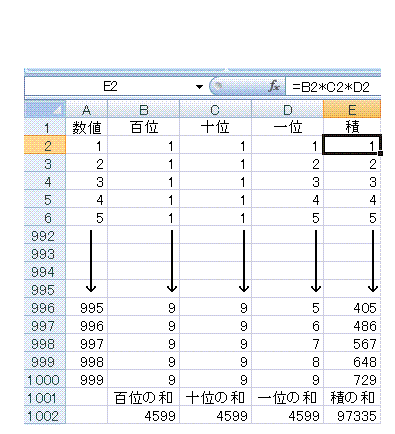
エクセルを使いました。
Ａセルの１をＢセルに０，Ｃセルに０，Ｄセルに１とに入力する。Ａセルの２５はＢセルに０，Ｃセルに２，Ｄセルに５と入力する。ＥセルにＢ＄×Ｃ＄×Ｄ＄の式を入力します。
Ｅセルの数式を９９９までコピーします。各行Ｅセルの計算結果が０の行のところはその行の各桁のどれかに０が入っていますので０を１にします。そして、合計の結果を見ます。答えは９７３３５です。

---

解答・その4

（ペンネ−ム：オヤジ）

１．ａ（０）＝０　と定義すると、ａ（ｐｑｒ）＝ａ（ｐ）＋ａ（ｑ）＋ａ（ｒ）となる。
　　　ａ（１）＋ａ（２）＋・・・・＋ａ（９）＝１＋２＋・・・＋９＝４５　・・・（�T）
　　　ａ（１０）＋ａ（１１）＋・・・・＋ａ（１９）＝１０×ａ（１）＋（�T）＝５５
　　　ａ（２０）＋ａ（２１）＋・・・・＋ａ（２９）＝１０×ａ（２）＋（�T）＝６５
　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
　　　ａ（９０）＋ａ（９１）＋・・・・＋ａ（９９）＝１０×ａ（９）＋（�T）＝１３５
以上により
　　　ａ（１）＋ａ（２）＋・・・・＋ａ（９９）＝９００　・・・・・（�U）
　　　ａ（１００）＋ａ（１０１）＋・・・・＋ａ（１９９）＝１００×ａ（１）＋（�U）＝１０００
　　　ａ（２００）＋ａ（２０１）＋・・・・＋ａ（２９９）＝１００×ａ（２）＋（�U）＝１１００
　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
　　　ａ（９００）＋ａ（９０１）＋・・・・＋ａ（９９９）＝１００×ａ（９）＋（�U）＝１８００
以上により
　　　ａ（１）＋ａ（２）＋・・・・＋ａ（９９９）＝１００×（�T）＋１０×（�U）＝１３５００
　　　　∴　　１３５００

２．
　　　ｂ（１）＋ｂ（２）＋・・・・＋ｂ（９）＝１＋２＋・・・＋９＝４５　・・・（�V）
　　　ｂ（１０）＋ｂ（１１）＋・・・・＋ｂ（１９）＝ｂ（１）＋１×（�V）＝　４６
　　　ｂ（２０）＋ｂ（２１）＋・・・・＋ｂ（２９）＝ｂ（２）＋２×（�V）＝　９２
　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
　　　ｂ（９０）＋ｂ（９１）＋・・・・＋ｂ（９９）＝ｂ（９）＋９×（�V）＝　４１４
以上により
　　　ｂ（１）＋ｂ（２）＋・・・・＋ｂ（９９）＝　２１１５　・・・・（�W）
　　　ｂ（１００）＋ｂ（１０１）＋・・・・＋ｂ（１９９）＝ｂ（１）＋１×（�W）＝２１１６
　　　ｂ（２００）＋ｂ（２０１）＋・・・・＋ｂ（２９９）＝ｂ（２）＋２×（�W）＝４２３２
　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
　　　ｂ（９００）＋ｂ（９０１）＋・・・・＋ｂ（９９９）＝ｂ（９）＋９×（�W）＝１９０４４
以上により
　　　ｂ（１）＋ｂ（２）＋・・・・＋ｂ（９９９）＝　（�V）＋４６×（�W）＝　９７３３５
　　　　∴　９７３３５

---

解答・その5

（ペンネ−ム：転位反応）

１． 先ず、1桁の整数について検討する。
a(1)+a(2)+・・・+a(9)
　=1+2+・・・+9
　=A とする。 ・・・(1)

次に、2桁の整数について検討する。
2桁の整数mnについて、a(mn)=m+n=a(m)+a(n)が成り立つので
a(10)+a(11)+・・・+a(19)
=a(1)×10+a(0)+a(1)+a(2)+・・・+a(9)
=10+1+2+・・・+9
=10+A
∴a(10)+a(11)+・・・+a(19)=A+10

同様にして、
a(20)+a(21)+・・・+a(29)=A+20
a(30)+a(31)+・・・+a(39)=A+30
　・・・
a(90)+a(91)+・・・+a(99)=A+90　
辺々を加えると、
a(10)+a(11)+・・・+a(99)=9A+10(1+2+・・・+9)
　 =9A+10A
　 =19A　　　　 ・・・(2)　　　
　
(1)+(2)から、a(1)+a(2)+・・・+a(99)=20A ・・・(3)　
更に、3桁の整数について検討する。
3桁の整数lmnについて、a(lmn)=l+(m+n)=a(l)+a(mn)が成り立つので
a(100)+a(101)+・・・+a(199)
=a(1)×100+a(0)+a(1)+a(2)+・・・+a(99)
=100+20A　　　(∵ (3)より)
∴a(100)+a(101)+・・・+a(199)=20A+100

同様にして、
a(200)+a(201)+・・・+a(299)=20A+200
a(300)+a(301)+・・・+a(399)=20A+300
　・・・
a(900)+a(901)+・・・+a(999)=20A+900

辺々を加えると、
a(100)+a(101)+・・・+a(999)=20A×9+100(1+2+・・・+9)
　 =180A+100A
　 =280A

∴a(1)+a(2)+・・・+a(999)
　　=300A
=13500 (∵ A=45)

２．先ず、1桁の整数について検討する。
b(1)+b(2)+・・・+b(9)
　=1+2+・・・+9
　=B とする。 ・・・(1)

次に、2桁の整数について検討する。
b(10)+b(11)+・・・+b(19)
=1+1+2+3+・・・+9
=1+B
∴b(10)+b(11)+・・・+b(19)=B+1

同様にして、
b(20)+b(21)+・・・+b(29)=2(B+1)
b(30)+b(31)+・・・+b(39)=3(B+1)
　・・・
b(90)+b(91)+・・・+b(99)=9(B+1)

辺々を加えると、
b(10)+b(11)+・・・+b(99)=(1+2+・・・+9)(B+1)
　 =B(B+1)　　　　 ・・・(2)

更に、3桁の整数について検討する。
b(100)+b(101)+・・・+b(109)=1+1+2+3+・・・+9=B+1
b(110)+b(111)+・・・+b(119)=1+1+2+3+・・・+9=B+1
b(120)+b(121)+・・・+b(129)=2+2(1+2+3+・・・+9)=2(B+1)
b(130)+b(131)+・・・+b(139)=3+3(1+2+3+・・・+9)=3(B+1)
　・・・
b(190)+b(191)+・・・+b(199)=9+9(1+2+3+・・・+9)=9(B+1)

辺々を加えると、
b(100)+b(101)+・・・+b(199)
=(B+1)(1+1+2+・・・+9)
=(B+1)(1+B)
=(B+1)2

同様にして、
b(200)+b(201)+・・・+b(299)=2(B+1)2
b(300)+b(301)+・・・+b(399)=3(B+1)2
　・・・
b(900)+b(901)+・・・+b(999)=9(B+1)2

辺々を加えると、
b(100)+b(101)+・・・+b(999)=(1+2+・・・+9)(B+1)2
=B(B+1)2　　・・・(3)

(1)+(2)+(3)から、
　　b(1)+b(2)+・・・+b(999)
　　=B(B+1)2+B(B+1)+B
=97335　　　　 (∵ B=45)

---

解答・その6

（ペンネ−ム：のっこん）

（１）
000から999までは全部で1000個
各々3個の数字からできているから数字は全部で3000個
0、1、2、・・・・、9の出現度数は等しいから
3000個の内訳は
0が300個、1が300個、・・・・、9が300個
よって与式=300(1+2+・・・・+9)=300・45=13500

（２）
b(1)〜b(99)を次に記す

　　　b(1)〜b(9) 　　　　　　1 2 3 4 5 6 7 8 9
　　　b(10)〜b(19)　　　1 1 2 3 4 5 6 7 8 9
　　　b(20)〜b(29)　　　2 2 4 6 8 10 12 14 16 18
　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
　　　b(90)〜b(99) 9 9 18 27 36 45 54 63 72 81

1+2+・・・・+9=A とすると
　　　b(1)+b(2)+・・・・+b(99)=A+A+A+2A+3A+・・・・+9A
　　　　　　　　　　　　　　　=2A+A・A=2・45+45・45=90+2025=2115

b(100)=1 だから
　　　b(100)+b(101)+・・・・+b(199)=1+b(1)+b(2)+・・・・+b(99)=1+2115=2116
b(100)+b(101)+・・・・+b(199)=B とすると
　　　b(200)+b(201)+・・・・+b(299)=2B
　　　b(300)+b(301)+・・・・+b(399)=3B
　　　　　　・・・・・・・・・・・・
　　　b(900)+b(901)+・・・・+b(999)=9B

よって与式=2115+B+2B+・・・・+9B
　　　　　=2115+B・A=2115+2116・45=97335

---

解答・その7

（ペンネ−ム：スモークマン）

(1)
000〜999 までの各桁の数字の和なので...
Σa(n)=(1+2+...+9)*10²*3=45*3*100=13500

(2)
0 ：1〜9...;2+...+9=45
10〜90 ：(1+2+...+9)*45=45²
100〜900 ：(1+2+...+9)*45²=45³

0でない桁の積も加える…
0 が1個のとき…二桁のときと三桁のとき...45+2*45²
0 が2個のとき...三桁のとき…45

けっきょく...
Σb(n)=3*45+3*45²+45³=97335

---

解答・その8

（ペンネ−ム：atsuhiro）

1.
　　　a(1)+a(2)+・・・+a(999)
　　=(1+2+3+4+5+6+7+8+9)*(100+100+100)
　　=13500

2.
nの百の位を k (0≦k≦9)とする。

�@)k=0のとき
　　　b(1)+b(2)+・・・+b(99)
　　={(1+2+3+4+5+6+7+8+9)
　　　　+(1+2+3+4+5+6+7+8+9)*1+1
　　　　+(1+2+3+4+5+6+7+8+9)*2+2
　　　　+・・・
　　　　+(1+2+3+4+5+6+7+8+9)*9+9}
　　=2115

�A)k≠0のとき
　　　b(k+1)+b(k+2)+・・・+b(k+99)
　　={(1+2+3+4+5+6+7+8+9)+1
　　　　+(1+2+3+4+5+6+7+8+9)*1+1
　　　　+(1+2+3+4+5+6+7+8+9)*2+2
　　　　+・・・
　　　　+(1+2+3+4+5+6+7+8+9)*9+9}*k
　　=2116k

よって
　　　b(1)+b(2)+・・・+b(999)
　　=2115+Σ[k=1〜9]2116k
　　=97335

---

解答・その9

（ペンネ−ム：MVH）

１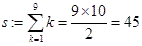）　　とするとき、０≦ｍ≦９を満たす任意の整数ｍに対して、

　　　
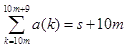
が成立しますから、

　　　
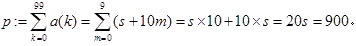
これを用いると、０≦ｍ≦９を満たす任意の整数ｍに対して、

　　　
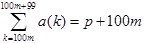
が成立しますから、求める総和は、

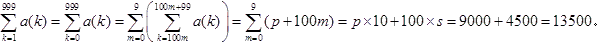　　　　　（答）

（２）まず、　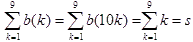　に注意します。
また、１≦ｍ≦９を満たす任意の整数ｍに対して、

　　　
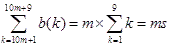
が成立しますから、

　　　
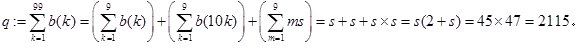
また、　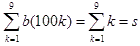　に注意します。 さらに、１≦ｍ≦９を満たす任意の整数に対して、

　　　
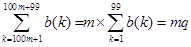
が成立しますから、求める総和は、

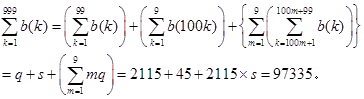　　　　（答）

---

解答・その10

（ペンネ−ム：龍馬）

n=100x+10y+z とおく。(x,y,zは0以上9以下の整数、(x,y,z)≠(0,0,0))

１．
z=1,2,・・・,9のとき、(x,y)は10・10=100通り存在する。
z=0のとき、(x,y)は(0,0)を除き、99通り存在する。
∴ 1〜999の一の位には、1,2,・・・,9が各100回、0が99回現れる。
十、百の位についても同様のことが言えるので、
a(1)+a(2)+・・・+a(999)={(1+2+・・・+9)・100+0・99}・3=13500・・・(答)

２．
定義より、b(n)=b(100x+10y+z)=x・b(10y+z) (x≠0) ・・・(ア)
同様に、　b(10y+z)=y・b(z) (y≠0)・・・(イ)
S=b(1)+・・・+b(99)とおくと、(ア)より、
b(1)+b(2)+・・・+b(999)=S+(1+2+・・・+9)S+{b(100)+b(200)+・・・+b(900)}=46S+45
T=b(1)+・・・+b(9) (=45) とおくと、(イ)より、
S=T+(1+2+・・・+9)T+{b(10)+b(20)+・・・+b(90)}=46T+45=2115
∴ b(1)+b(2)+・・・+b(999)=46S+45=46・2115+45=97335・・・(答)

---

解答・その11

（ペンネ−ム：三角定規）

１．i≦j として，a(i)＋…＋a(j)＝s(i，j) と書くことにする。
　(1) 1≦n≦9 のとき，a(n)＝n　　∴ s(1，9)＝1＋…＋9＝45 … <1>
　(2) 10≦n≦99 のとき，n＝10j＋i (1≦i，j≦9) として，a(n)＝a(10j＋i)＝j＋i
　　　　∴ s(10j，10j＋9)＝ｊ＋(j＋1)＋…＋(j＋9)＝10j＋45
　　　　∴ s(1，99)＝10(1＋…＋9)＋45×10＝900 … <2>
　(3) 100≦n≦999 のとき，n＝100k＋m (1≦k≦9，0≦m≦99) として，a(n)＝k＋a(m)
　　　　∴ s(100，999)＝100(1＋…＋9)＋900×9＝12,600　(∵<2>) …<3>
　　　　∴ s(1，999)＝900＋12600＝13,500 … [答]

２．b(0)＝1 とし，0≦i≦j として，b(i)＋…＋b(j)＝t(i，j) と書くことにする。
　(1) 1≦n≦9 のとき，b(n)＝n　　∴ t(1，9)＝1＋…＋9＝45 … <4>
　(2) 10≦n≦99 のとき，n＝10j (j＝1，…，9) ならば，b(n)＝j
　　　n＝10j＋i (1≦i，j≦9) ならば，b(n)＝b(10j＋i)＝ij
　　　　∴ t(10，99)＝(1＋45)×45＝2,070 … <5>
　　　　∴ t(1，99)＝t(1，9)＋t(10，99)＝45＋2,070＝2,115 … <6>
　(3) 100≦n≦999 のとき，n＝100k＋m (1≦k≦9，0≦m≦99) として，b(n)＝k・b(m)
　　　　∴ t(100，999)＝2,070(1＋1＋…＋9)＝2,070×46＝95,220　(∵<5>) …<7>
　　　　∴ t(1，999)＝t(1，99)＋t(100，999)＝2,115＋95,220＝97,335 … [答]

１．の別解
　数 n が１桁，２桁のとき，左に 0 をつけて‘３桁’にすると， 000〜999 の 1000 個の数の中，すなわち 3000 個の数字に 0〜9 は均等に 300 個ずつある。 よって，これらの数字の和は
　　　(1＋2＋…＋9)×300＝45×300＝13,500 … [答］

---

解答・その12

（ペンネ−ム：T_Tatekawa）

1. 1 から 999 について，
百の位が0のものは99個，0以外のものはそれぞれ100個．
十の位がが0のものは99個，0以外のものはそれぞれ100個．
一の位がが0のものは99個，0以外のものはそれぞれ100個．

1から9までの整数の和は
　　(1+9)*9/2 = 45．

よって，

　　　a(1)+a(2)+...+a(999)
　　= 45*100*3
　　= 13500

2. まず
　　b(1)+...+b(9) = 45
次に2桁の数を考えると，
　　b(10)+b(20)+...+b(90)=1+2+...+9=45
0を含まない2桁の数については
　　　b(11)+b(12)+...+b(99)
　　=(1+2+..+9)*(1+2+...9)
　　=45*45
　　=2025
3桁の数を考えると、
　　b(100)+b(200)+...+b(900)=45
十の位が0の数については，
　　b(101)+b(102)+...+b(909)=45*45=2025
一の位が0の数については，
　　b(110)+b(120)+...+b(990)=45*45=2025
0を含まない3桁の数については
　　b(111)+b(112)+...+b(999)=45*45*45=91125

以上をまとめると，
　　　45+(45+2025)+(45+2025+2025+91125)
　　=97335

---

解答・その13

（ペンネ−ム：夜ふかしのつらいおじさん）

各位の数字の和を考えるとき、0も仲間に入れる方がきれいにいくのでそうします。
もちろん答えに影響はありません。縦に0から999まで数を並べたとします。

0
1
2
・・・
9
10
11
12
・・・
999

(1)1の位だけを縦にみていくと、｛0,1,2,3,4,5,6,7,8,9｝の繰り返しです。
　　これが1000／10＝100個あります。
(2)10の位だけをみていくと、｛0が10個、1が10個、2が10個、・・・、9が10個｝の繰り返しです。
　　これが1000／(10×10)＝10個あります。
(3)100の位だけをみていくと、｛0が100個、1が100個、2が100個、・・・、9が100個｝の繰り返しです。
　　これが1000／(100×10)＝1個あります。

以上から、

　　　

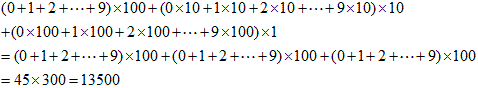
となります。

２．各位の数字の積の場合は、0は仲間に入れません。
(1)b(1)＋b(2)＋b(3)＋・・・＋b(9)＝1＋2＋3＋・・・＋9＝45を確認しておきます。
(2)下2桁が0の数を考えます。
　　　b(100)＋b(200)＋b(300)＋・・・＋b(900)＝1＋2＋3＋・・・＋9＝45です。
(3)下1桁が0の2桁の数を考えます。
　　　b(10)＋b(20)＋b(30)＋・・・＋b(90)＝1＋2＋3＋・・・＋9＝45です。
(4)下1桁が0でない2桁の数を考えます。
　　　b(11)＋b(12)＋b(13)＋・・・＋b(19)＝1×1＋1×2＋1×3＋・・・＋1×9＝1×45
　　　b(21)＋b(22)＋b(23)＋・・・＋b(29)＝2×1＋2×2＋2×3＋・・・＋2×9＝2×45
　　　　・・・
　　　b(91)＋b(92)＋b(93)＋・・・＋b(99)＝9×1＋9×2＋9×3＋・・・＋9×9＝9×45
小計が、45×45
(5)下1桁が0の3桁の数を考えます。
　　　b(110)＋b(120)＋b(130)＋・・・＋b(190)＝1×1＋1×2＋1×3＋・・・＋1×9＝1×45
　　　b(210)＋b(220)＋b(230)＋・・・＋b(290)＝2×1＋2×2＋2×3＋・・・＋2×9＝2×45
　　　　・・・
　　　b(910)＋b(920)＋b(930)＋・・・＋b(990)＝9×1＋9×2＋9×3＋・・・＋9×9＝9×45
小計が、45×45
(6)下1桁が0でない3桁の数を考えます。
　　・b(101)＋b(102)＋b(103)＋・・・＋b(109)＝1×1＋1×2＋1×3＋・・・＋1×9＝1×45
　　　b(111)＋b(112)＋b(113)＋・・・＋b(119)＝1×1＋1×2＋1×3＋・・・＋1×9＝1×45
　　　b(121)＋b(122)＋b(123)＋・・・＋b(129)＝2×1＋2×2＋2×3＋・・・＋2×9＝2×45
　　　　・・・
　　　b(191)＋b(192)＋b(193)＋・・・＋b(199)＝9×1＋9×2＋9×3＋・・・＋9×9＝9×45
小計が、1×45＋1×45×45
　　・b(201)＋b(202)＋b(203)＋・・・＋b(209)＝2×(1×1＋1×2＋1×3＋・・・＋1×9)＝2×1×45
　　　b(211)＋b(212)＋b(213)＋・・・＋b(219)＝2×(1×1＋1×2＋1×3＋・・・＋1×9)＝2×1×45
　　　b(221)＋b(222)＋b(223)＋・・・＋b(229)＝2×(2×1＋2×2＋2×3＋・・・＋2×9)＝2×2×45
　　　　・・・
　　　b(291)＋b(292)＋b(293)＋・・・＋b(299)＝2×(9×1＋9×2＋9×3＋・・・＋9×9)＝2×9×45
小計が、2×45＋2×45×45
　　　　・・・・
　　・b(901)＋b(902)＋b(903)＋・・・＋b(909)＝2×(1×1＋1×2＋1×3＋・・・＋1×9)＝9×1×45
　　　b(911)＋b(912)＋b(913)＋・・・＋b(919)＝2×(1×1＋1×2＋1×3＋・・・＋1×9)＝9×1×45
　　　b(921)＋b(922)＋b(923)＋・・・＋b(929)＝2×(2×1＋2×2＋2×3＋・・・＋2×9)＝9×2×45
　　　　・・・
　　　b(991)＋b(992)＋b(993)＋・・・＋b(999)＝2×(9×1＋9×2＋9×3＋・・・＋9×9)＝9×9×45
小計が、9×45＋9×45×45
(6)の合計は、45×45＋45×45×45

以上から、
　　　　45＋45＋45+45×45＋45×45＋45×45＋45×45×45
　　　＝3×45＋3×45×45＋45×45×45
　　　＝97335

---

解答・その14

（ペンネ−ム：迷子の雄猫）

１．
ａ(０)＝ａ(０００)＝０　ａ(１)＝ａ(００１)＝１であるので、
ａ(１)＋ａ(２)＋・・・＋ａ(９９９)を求める代わりに、 ａ(０００)＋ａ(００１)＋ａ(００２)＋・・・＋ａ(９９９)を求めても同じである。

さて、１の位だけ考えてみよう。
ａ(？？０)＋ａ(？？１)＋ａ(？？２)＋・・・＋ａ(？？９)は、
ａ(１２３４５６７８９）であるので４５。？？の部分は００〜９９までの１００個あるので 合計は４５００である。１０の位、１００の位も同様であるので、答えは１３５００。

２．
さて、ｂ（０）＝１、ｂ（１）＝ｂ（００１）＝１である。
１の位だけ考えてみよう。
ｂ(？？０)＋ｂ(？？１)＋ｂ(？？２)＋・・・＋ｂ(？？９)は、
ｂ(？？）の４６倍。？？の部分は００〜９９までの１００個ある。
ｂ(？０)＋ｂ(？１)＋ｂ(？２)＋・・・＋ｂ(？９)は、ｂ(？）の４６倍。
？の部分は０〜９までの１０個ある。
よって結局、ｂ(０)＋ｂ(１)＋ｂ(２)＋・・・＋ｂ(９９９)は、４６の三乗で９７３３６。
よってｂ(１)＋ｂ(２)＋・・・＋ｂ(９９９)は９７３３５。

---

解答・その15

（ペンネ−ム：haya）

(1) a(1)+a(2)+ … +a(999)=13500
(2) b(1)+b(2)+ … +b(999)=97335

【解き方】

(1)　各桁の和は何れも

　　　(1+2+3+4+5+6+7+8+9)*100=4500
で、3桁あるから
　　　a(1)+a(2)+…+a(999)=4500*3=13500

(2)　「0でない各桁の数字の積」を「各桁の数字で0を1に置き換えた積」と読み替えて計算する。
2-1) b(1)〜b(9)の範囲では、
　　　b(1)+b(2)+…+b(9)=(1*1)*(1+2+…+9)=45
2-2) b(10)〜b(99)の範囲では、
　　1の桁は1, 1, 2, 3, 4, 5, 6, 7, 8, 9の変化を周期的に繰り返し、それぞれに対して上位の桁は1*1, 1*2, 1*3, …, 1*9と変化するから、
　　　b(10)+b(11)+…+b(99)=(1*1+1*2+1*3+…+1*9)(1+1+2+3+…+9)=45*46=2070
2-3) b(100)〜b(999)の範囲では、
　　1の桁は同上、上位の桁は、1*1, 1*2, …, 1*9, 2*1, 2*2, …, 9*9まで変化するが、中央の桁の0を1と読み替えたことによって、2-2)と同一成分があることにも注意して、
　　　　b(100)+b(101)+…+b(999)
　　　=b(10)+b(11)+…+b(99)+(1*1+1*2+…+1*9+2*1+2*2+…+9*8)*((1+1+2+3+…+9)
　　　=2070+2025*46=2070+93150=95220
よって求める答は、
　　　b(1)+b(2)+…+b(999)=45+2070+95220=97335

---

解答・その16

（ペンネ−ム：falcon@中学教師）

＜答え＞
（１）１３５００
（２）９７３３５

＜考え方＞
（１）
上２桁が00であるnについて、a(n)の総和は４５
上２桁が01であるnについて、a(n)の総和は５５
・
・
・
上２桁が09であるnについて、a(n)の総和は１３５
さらにこれらの総和、つまり上１桁が0であるnについてのa(n)の総和は９００となる。
同様にして上1桁がmであるnについてのa(n)の総和を求め、c(m)と表現することにする。

　　　 a(1)+a(2)+・・・+a(999)
　　　=c(0)+c(1)+・・・+c(9)
　　　=900+1000+・・・+1800
　　　=13500

（２）
それぞれの位の数は０〜９であり、3桁の位の数をかけたものの総和は、 (0+1+2+・・・+9)の３乗になる。
しかし、今回の問題では０は無視するので、位に０が現れたときは代わりに１をかけていると考えると、 (1+1+2+・・・+9)の３乗になる。
さらにこれではn=000という数字を考えているので、１を引く。
よって
　　　 b(1)+b(2)+・・・+b(999)
　　　=(1+1+2+・・・+9)³-1
　　　=46³-1
　　　=97336-1
　　　=97335

---

解答・その17

（ペンネ−ム：teki）

１　　１３５００
これは単純ですね。
０〜９が１００個ずつ各桁にあるので、４５×１００×３＝１３５００

２　　９７３３５
まともに計算するにはプログラムでも組まないと無理ですが、 ちょっと工夫すれば何とか計算できます。
１〜９９９ではなく、０〜９９９で考えます。
０〜９９９を無理矢理３桁にします。（０→０００、１→００１・・・・・・・・）
で、この０を１に置き換えます。
すると、１１１，１１１，１１２・・・・・・・９９９となりますが、これの各桁は１＋４５＝４６です。
よって題意の合計は、４６×４６×４６−１＝９７３３５。（最後の−１は０の分）

---

解答・その18

（ペンネ−ム：マシャ）

1【解答】
a(0) = 0 なのでa(0) + … + a(999)を考えても良い
各桁に表れる数字の個数を考えると 000から999までなので, それぞれ100個ずつ現れる.
最大桁数は3桁なので3通り存在する.
　　　(0+1+…+9)*100*3 = 13500
答え 13500

【過程】
まず例にいくつか値を求めようと
　　　a(1) = 1
　　　a(9) = 9
　　　a(10) = 1+0
　　　a(11) = 1+1
と"縦"に書いたら 「横に考えるのではなく縦に考えたら？」 と思い, 数字の出現パターンに気がつきました.

2【解答】
各桁に0が表れる個数によって場合分けする.
(但し, 1, 10などは001, 010と考える)
(i) 0が3個の場合
　　　000のみなので
　　　0

(ii)0が2個の場合
001から009とその0の位置に関して3通りなので
　　　(1+…+9)*3

(iii)0が1個の場合
011から099とその0の位置に関して3通りなので 積の和を以下のように因数分解できる
　　　(1+…+9)*(1+…+9)*3

(iv)0が0個の場合
(iii)と同様に考えて
　　　(1+…+9)*(1+…+9)*(1+…+9)

(i)から(iv)より
　　　　0+(1+…+9)*3+(1+…+9)*(1+…+9)*3+(1+…+9)*(1+…+9)*(1+…+9)
　　　={(1+…+9)+1}³ - 1
　　　=97335

答え 97335
【過程】
1問目がヒントになり"0"を陽に考えて辿り着きました.
また, 計算が大変そうなので後に残しておいたら
なんと因数分解(もどき)になり少しだけ計算が楽になりました.

【コメント】
最後の計算に3乗が現れたので, もしかしたらもっとエレガントな解法があるのではないか と期待しています.
n進数で0から(n-1)(n-1)(n-1)(n進数表示)の場合は
1問目 3n³(n-1)/2
2問目 {(n²-n+2)/2}³ - 1 = n(n-1)(n⁴-2n³+7n²-6n+12)/8

あんまり美しい形にはなりませんでした…

---

解答・その19

（ペンネ−ム：ちょろんは太太）

(1)
a(n)+a(999-n)を考える。
ｎのそれぞれの位の数を s, t, u とすれば、999-n のそれぞれの位は、9-s, 9-t, 9-u
　　　a(n)+a(999-n)=s+t+u+(9-s)+(9-t)+(9-u)=27
よって、
　　　 a(1)+a(2)+･･･+a(998)+a(999)=(27×998)/2+a(999)=27×500=13500

(2)
100の位をs、10の位をt、１の位をuとしたとき、 999までの正の整数は、s=0,1,…8,9t=0,1,…8,9u=0,1,…8,9から　 s、t、uを一つずつ取り出したすべての組み合わせ。ただし、s=t=u=0は除く。
s、t、uのすべての組み合わせの積s×t×uの総和は、
　　　 (sの総和)×(tの総和)×(uの総和)　ただし、s=t=u=0の分は差し引く。
また、数字が0である場合は、ｂ(n)は、それ以外の数の積とするので、 0は、'1'の積として作用する。以上をまとめると、
　　　(b(1)+b(2)+･･･+b(998)+b(999)
　　＝(1+1+2+3+･･･+8+9)×(1+1+2+3+･･･+8+9)×(1+1+2+3+･･･+8+9)-b(000)
　　＝46×46×46-1=97335

正解者

haya	夜ふかしのつらいおじさん	のっこん
スモークマン	エルドス	falcon@中学教師
龍馬	転位反応	迷子の雄猫
マシャ	オヤジ	ちょろんは太太
atsuhiro	浜田　明巳	杖のおじさん
MVH	teki	T_Tatekawa
三角定規

コメント

今月、11日に東日本大震災が起きました。亡くなられた方々のご冥福をお祈りするとともに、 被災された方々に心からお見舞い申し上げます。 一刻も早い被災地の復興のために何ができるのか、 これから先、どういう生き方をしていったらよいのか、私自身、そしてすべての人が 問われているのではないかと思います。

今回の問題は、１から９９９までの数の各桁の数字の和と積を求める問題でした。 １．は、和を求める問題です。加法における単位元は、「０」ですから、 「０」を無視することができます。 一方、２．は積を求める問題です。乗法において、「０」は無視できませんので、 根気強く場合分けをしていく必要があるわけですが、この「０」を乗法の単位元である 「１」に置き換えたら、見通しが良くなりますね。

単位元
ある集合の要素に演算＊が定義されていたとする。 この集合の任意の要素ａに対して、
　　　ａ＊ｅ＝ｅ＊ａ＝ａ
となるｅを単位元といいます。
整数の集合における加法と乗法を考えると、加法の単位元は「０」、乗法の単位元は「１」ですね。

---