���170�@���O�p�`�̖��
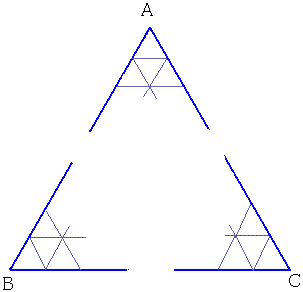 �P�ӂ̒�����30�ł��鐳�O�p�`�`�a�b������B
������A�P�ӂ̒������P�̏����O�p�`�ɕ�������B
�P�ӂ̒�����30�ł��鐳�O�p�`�`�a�b������B
������A�P�ӂ̒������P�̏����O�p�`�ɕ�������B
(1)�@�S���ł����̏����O�p�`�ɕ�����܂����B
(2)�@�ӂa�b��ɁA�a�o���P�O�ƂȂ�_�o���Ƃ�B
�����`�o�ɂ���ĂQ�̕����ɕ������鏬���O�p�`�͂������邩�B
(3)�@�ӂ`�a��ɓ_�p���A�ӂa�b��ɓ_�q���A�ӂb�`��ɓ_�r���A
���ꂼ��`�p���a�q���b�r���R�D�R�R�R�ƂȂ�悤�ɂƂ�B
�O�p�`�p�q�r�̎����ʂ鏬���O�p�`�͂������邩�B
(4)�@�O�p�`�`�a�b���A�P�ӂ̒������P�̐��O�p�`�i���j�ƁA
�i���j��}�̂悤�ɂQ�����������^�C���i���j��p���āA
�^�C�����d�˂邱�ƂȂ����������B
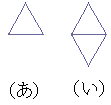
���̂Ƃ��A�i���j�̃^�C���͏��Ȃ��Ƃ������K�v�ɂȂ�ł��傤���B
���̏o�T
�L���t�@�n�C���x�����w���w�ɒ���
�u�k��
2004�N��T��t�@�C�i�����
��
�E����1
�i�y���l�|���F������͑����j
(1) �O�p�`�����̐����Ȑ��̏㉺�ɐ��̒����Ɠ������̏����O�p�`������A
�����R�O�̒�ӂɂ́A�㑤�����ɏ����O�p�`������B��������ׂĉ�����ƁA
�@�@�@ (1+2+3+���+29)�~2+30=(29�~(1+29))/2�~2+30=900�@
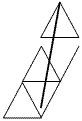 (2) ����AP�́AA����R�O�i�������āA�P�O���E�ɂ��̂�����A�R�i�������āA�P���E�ɂ��A�S�i�ڂ̏��O�p�`�̒��_��ʂ�B���̊Ԃɂ悬�鏬���O�p�`�́A�S�B������P�O��J��Ԃ��̂ŁA�������ʉ߂��鏬���O�p�`�́A�S���ŁA
(2) ����AP�́AA����R�O�i�������āA�P�O���E�ɂ��̂�����A�R�i�������āA�P���E�ɂ��A�S�i�ڂ̏��O�p�`�̒��_��ʂ�B���̊Ԃɂ悬�鏬���O�p�`�́A�S�B������P�O��J��Ԃ��̂ŁA�������ʉ߂��鏬���O�p�`�́A�S���ŁA
�@�@�@4�~10=40
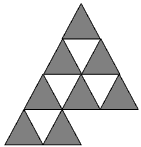 (4)���̂悤�ɁA�F��������ƁA���������O�p�`�́A
(4)���̂悤�ɁA�F��������ƁA���������O�p�`�́A
�@�@�@1+2+���+29=((29+1)�~29)/2=435
���������O�p�`�́A
�@�@�@1+2+���+30=((30+1)�~30)/2=465
�i���j�̃^�C���ŁA�����ƕK���A���ƍ��̕�����1�������B
�]���āA�i���j���ł��邾�������g���Ƃ��Ă��A�S�R�T���܂ŁB
�S�R�T�����̍��̕����́A�i���j�ŕ������Ƃ��ł��邪�A
�@�@�@465-435=30
�́A�i���j�̃^�C�����K�v�ɂȂ�B
�E����2
�i�y���l�|���F�X���[�N�}���j
(1) 1+3+5+...+(2*29+1)=1+3+5+...+59=60*30/2=900 ��
�@�ʐς���...302/12=900 ��
(2) 10/59...�����łȂ��̂�...�i�i�̐��O�p�`�Q�ʂ�...
�@�ŏ��ƍŌ��1�ɂȂ�̂�...2*28+2=58 ��
(4) �i�i��Ȃ̂�...�傫���O�p�`�̊O���̂Q���_�̓y�A�ł͖���...
�@30/2=15...2*15=30 ����(��)���K�v...
�ō����Ă邩��...?
�E����3
�i�y���l�|���F�I���W�j
�i�P�j
�P�{�R�{�T�{�E�E�E�{�i�Q���|�P�j�����Q�@���@���߂���́A
�@�@�@�P�{�R�{�T�{�E�E�E�{�i�Q�~�R�O�|�P�j���R�O�Q���X�O�O
���@�X�O�O��
�i�Q�j
�}�̐��O�p�`�`�a�b�ɁAB�i�O�C�O�j�C�`�i�O�C�R�O�j�C�b�i�R�O�C�O�j�ƂȂ�悤��
�_�s�i���C���j�Ƃ��邘�����̎Ό����W�������B�o�i�P�O�C�O�j�ƂȂ邩��A
�]���Ē����`�o�́A
�@�@�@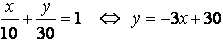
�܂��A���O�p�`�̒��_�́A��,���Ƃ��ɂO�ȏ�̐����̊i�q�_�ƂȂ�
�����`�o�́A�P�P�̊i�q�_�i�O�C�R�O�j�C�i�P�C�Q�V�j�E�E�E�i�X�C�R�j�C�i�P�O�C�O�j��ʂ�
�e�i�q�_�ԂŐ����`�o�́A�S�̏��O�p�`��ʂ�̂ŁA�]����
�@�@�@�S�~�P�O���S�O
���@�S�O��
�i�S�j
��ʂɁ@��ӂ��̐��O�p�`�ł́A�i���j�́A�ō��@��(���|�P)/2�@�A�i���j�́A�Œ�@���@�@�K�v
�@�@�@��@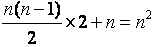
���@�R�O��
�E����4
�i�y���l�|���F�o���^�����l�j
�����F
(1) �X�O�O�C(2) �S�O�C(4) �R�O
�l�����F
�P�j�i�P�{�Q�{�E�E�E�E�{�Q�X�j�~�Q�{�R�O���R�O�~�R�O���X�O�O
�@�@�ʉ��F������R�O�̂Q��łX�O�O
�Q�j�@��_��ʂ�㉺�͂P�A����ȊO�͂Q�́�����B
�@�@���͐��������P�F�Q�ɕ�����_��ʂ�̂Œ������R�̔{���̎��A��_��ʂ�B
�@�@�@�i�P�{�Q�{�P�j�~�P�O���S�O
�S�j���_�������܂ށ������ɂʂ�s���͗l�ɓh�蕪����ƍ��������R�O�����Ȃ�̂Łi���j�͂R�O�K�v
�E����5
�i�y���l�|���FRyu1128�j
��1
��ӂ́u���O�p�`�v���u��ӂ�1�̏��O�p�`�v�Ɠǂ݉��܂��B�i����ȊO�̏�
�O�p�`�̋L�q�������̂Łj
��1
�@���́u�P��30�̐��O�p�`���P�ӂP�̐��O�p�`�ɕ����v�Ƃ���܂�������́A
�u�P�ӂP���O�p�`�ƂP�ӂ����̂R�O�{�̐��O�p�`�v�Ɠ��l�ł��B
���������āA�u�����`�̕��ʐ}�`�́A�ӂ̒��������{�ɂȂ�Ζʐς͂��̂Q���
�Ȃ�v���K�p�ł��܂��B
����āA30��2���900���̏��O�p�`���o���܂��B
��2
�@���ځ@�@1
�@���ځ@�@3
�@�O��ځ@�@5
�@�l��ځ@�@7
�@�E�E�E
�@����ځ@�@2��-1
���̓�������̘a�����߂�Ɓi1+�i2��-1�j�j�~��/2����2
��1�Ɠ������ʂƂȂ�܂�
���݂Ɂi�q�ǂ��ɐ����������@�ł����j�낪�������O�p�`�Ƌt���܂̐��O�p�`
�ɕ������
| �낪���� | �t���� | |
|---|---|---|
| ���� | 1 | 0 |
| ���� | 2 | 1 |
| �E�E�E | �@ | �@ |
| ����� | �� | ��-1 |
���̑��a�Ȃ̂Ő낪�����ق��͂��i��+1�j/2�t���܂̂ق��ɂ��𑫂��Ă��� �Ђ����i��+1�j/2-��
���̍��v���v�Z���Ă���2�ƂȂ�܂��B
�i�����P�̓�������̘a�͈�ԍŏ��Ɋw�т܂��̂Łj
�R
��1�̔h���ł����������g�|���W�J���ɍl���Đ��O�p�`�𐳕��`�ɕς��܂� �}�̐������̗�i�s�ƌ����ׂ����j�ɓ�����܂��B���̐}����S�̂̌� �����ӂ̔{���̂Q��ɔ�Ⴗ��̂�����܂��B
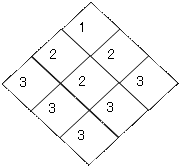
�l�@
���̖��͗��̂Ɋg���ł��܂��ˁB���S�ʑ̂œ�����������27000�̎l
�ʑ̂ɂȂ�܂��B�����̂ōl����ƊȒP�Ȗ��ł�������Ȃ��`�ɂȂ�ƌ˘f������
�ł��ˁB
��2
�悸�A�i���̕��͂̒��ł̂݁j�O�p�`�y�я��O�p�`�̐��������ӂƌĂт܂��B
����2�ӂ��ΕӂƌĂт܂��B�܂����Ƃ̎O�p�`���O�p�`�ƌĂт���ɑ����ȎO�p�`��
�O�p�`�ƌĂт܂��B
�����`�o�����O�p�`�̒��_��ʂ�ꍇ�͂��̒��_�̏㉺�i�͏��O�p�`�����������
�i��j�܂���B���_��ʂ�Ȃ��ꍇ�Εӂ��̂ŎΕӂ�����i�ł�2�̏��O
�p�`���܂��B�i��O�p�`�̓����i0���a�o���a�b�j�ł͓����i�ׂ̗荇�������O
�p�`�͎Εӂ����L���Ă���̂Łj
�����`�o���A���_��ʂ邩���v�Z����Ə�L���番������i����j���O�p
�`������܂��B
��{�I�ɂ͑S�Ă̒i�ŎΕӂ�����Ƃ�����i�i�����30�ł����j�����2����
�̏��O�p�`�����邱�ƂɂȂ�܂��B�Ƃ��낪��L�̒ʂ菬�O�p�`�̒��_��ʂ��
���Εӂ����Ȃ��̂Œ��_��ʂ邽�тɐ������2�����邱�ƂɂȂ��
���B
���ɍŏ�i�ƍʼn��i�����_��ʂ�ꍇ�͍��킹��2����ƍl����ƈ�ʉ����₷��
�Ǝv���܂��B
���`�a�o�Ƒ�O�p�`�̎ΕӂƂ��i�ڂ̒�ӂ̌�_���a�L�Ƃ����i�ڂ̒�ӂ̌�_�Ɛ�
���`�o�Ƃ̌�_���o�L�Ƃ��܂��B���`�a�o�ƃ��`�a�L�o�L�͑����ł��B
����ɂa�L�o�L�����R���ɂȂ�ꍇ�����`�o�͏��O�p�`�̒��_��ʂ�܂��B
���̎��R����T�����߂ɏ����v�Z���܂�
�`�a�F�a�o���`�a�L�F�a�L�o�L��30�F10�E�E(1)
�a�L�o�L���`�a�L�~�a�o/�`�a���`�a�L�~�a�o/�����`�a�L�~10/30���`�a�L�~1/3�E�E�E(2)
�a�L�o�L�����R���ƂȂ�̂͂`�a�L��3�̔{���ł��肻�̐��́i�ŏ㉺�i�����킹��1
�Ƃ���Ɓj30/3��10�ł��B
�i�����ła�L�o�L�����R���ƂȂ�̂�(2)�̉E�ӂ������ɂ��A���̕���ɒ��ڂ�
�܂��B���������Ă`�o��20�̏ꍇ�ƌ��ʂ͓����ɂȂ�܂��j
���鐔�͎Εӂ��S�Đ���ꍇ���10�~2��20����̂�30�~2-20��40�ł���
�ꍇ�̉�40�ƂȂ�܂����B
���̖��̑�ӂ́A���̏��O�p�`���邩�Ƃ���
��蒸�_������ʂ�̂��Ƃ������������C�����܂��B
�`�o�����R���ł��i�̎O�p�`�̏ꍇ�ōl����ƒ��_��ʂ�͍ŏ㉺�i���킹��
1�Ƃ����
�@�@�@�T�@���i���̖��ł͂`�a�j���f���̏ꍇ1�E�E�㉺�i�������_�͒ʂ�Ȃ�
�@�@�@�U�@���������̏ꍇ�@�����ɂ��
�@�@�@�@�@�@�@�����ɂ`�o���܂ޏꍇ�͒��_��ʂ�B�ʂ�͂�/�`�o�̊����̕���ł������������B
�����ɂ`�o���܂܂Ȃ��ꍇ�i�`�o�Ƃ����݂��ɑf�j�͏㉺�i�������_�͒ʂ�Ȃ��B�T�Ɠ���
���āA�ǂ�ȑ傫�Ȃ���I��ł�1���`�o����-1��K���ɑI�ׂΌ����ď��O�p�`�̒�
�_��ʂ�Ȃ��悤�Ȃo��I�Ԃ��Ƃ͉\�ł��傤���B�i�Ȃɂ��Ã̂悤�ɂȂ��Ă�
�܂��܂������j�E�E�E�B
���̓����͕s�\�ł��B
����f����̐ςɑI�ׂA�`�o�i1���`�o����-1�j�̑f�����͕K�����̒��Ɋ܂܂��
�̂ł��Ƃ`�o���݂��ɑf�Ƃ͂Ȃ�Ȃ�����ł��B
�t�ɁA�����ǂ�Ȃɑ傫���Ƃ��f���ɑI�ׂo���ǂ��ɂ����Ă��A�㉺�i�ȊO�̏��O
�p�`�̒��_�͒ʂ�܂���ˁB
�֑��ł����A���������̏ꍇ�A��O�p�`���ŏ��ɂ���̂͂`�o����/2�i�܂蒆
���j�ł��̐��͂��ɂȂ邱�Ƃ͎����ł��B
�E����6
�i�y���l�|���FT_Tatekawa�j
(1) ���������ɗ�ɂ�����`���l����ƁC
��ӂ̒����Ɖ��ӂ̒����̘a�������O�p�`�̐��ɔ�Ⴗ��D
�@�@1+(1+2)+(2+3)+...+(29+30)
�@�@= 29 x (29+1) + 30
�@�@= 900 (=302)
(3) �܂��O�p�` AQS, BRQ, CSR �ɂ��āC
AQ=BR=CS�CSA=QB=RC�C�pA=�pB=�pC �Ȃ̂ŁC
�����̎O�p�`�͍����ł���D
����āC�O�p�`QRS�̈�ӂ��ʂ鏬���O�p�`�̐��𐔂��C3�{����悢�D
��QR �ɒ��ڂ���D
�_Q�́u30�i�v�̏ォ��4�i�ڂɈʒu����D����QR�̌X���͕�AB���}�ł���D
�܂�����QR�͐��O�p�`�̒��_�ƌ������Ȃ��D
�_Q���܂ޒi�������āC1�i�ʂ邲�Ƃɏ����O�p�`��2�ʂ�D
�_Q���܂ޒi�͏����O�p�`��1�ʂ�D
����āC����QR���ʂ鏬���O�p�`�̐���
�@�@(30-4)x2 + 1 = 53��
����RS���l����ƁC��ԉ��̒i��2�̏����O�p�`�͐���QR�C����RS�������Ƃ�
�ʂ�D�d���x���l������3�{����ƁC���߂铚����
�@�@(53-2) x 3 = 153��
 (4) ���̐��O�p�`�ŁC�_A���܂ޏ����O�p�`�������h��D���ɂ��̏����O�p�`��
�אڂ��鏬���O�p�`�𔒂��h��D�Ȍ�C�����h���������O�p�`�ɗאڂ���
�����O�p�`�����ɁC�����h���������O�p�`�ɗאڂ��鏬���O�p�`�𔒂ɂ���D
�h��I������Ƃ���ŕ�AB�̑����琅�������E���Ɋe�i�����Ă����ƁC
���C���C���C��...�Ə����O�p�`�����ԁD�����ĕ�CA�ƕӂ����L����
�����O�p�`���S�č����Ȃ�D
(4) ���̐��O�p�`�ŁC�_A���܂ޏ����O�p�`�������h��D���ɂ��̏����O�p�`��
�אڂ��鏬���O�p�`�𔒂��h��D�Ȍ�C�����h���������O�p�`�ɗאڂ���
�����O�p�`�����ɁC�����h���������O�p�`�ɗאڂ��鏬���O�p�`�𔒂ɂ���D
�h��I������Ƃ���ŕ�AB�̑����琅�������E���Ɋe�i�����Ă����ƁC
���C���C���C��...�Ə����O�p�`�����ԁD�����ĕ�CA�ƕӂ����L����
�����O�p�`���S�č����Ȃ�D
����������ƁC�i���j�̌����̏����O�p�`�͍��C�㉺�t���̏����O�p�`�͔���
����D
�i���j���㔼�������C�������𔒂ɂ��āC�h�����Ƃ���ɏd�˂Ă����ƁC
�ŏI�I�ɍ��̏����O�p�`��30�̂���D
����āi���j�͏��Ȃ��Ƃ�30���K�v�D
�E����7
�i�y���l�|���F�̂�����j
�i1�j���O�p�`�Ƃ`�a�b�̑������1�F30������ʐϔ��1�F900
����ď��O�p�`�͑S����900��
�i2�j1�ӂ̒�����3�ł��鐳�O�p�`�`�L�a�L�b�L���l����
�ӂa�L�b�L��ɂa�L�o�L=1�ƂȂ�_�o�L���Ƃ�ƒ����`�L�o�L�ɂ����
4�̏����O�p�`��2�̕����ɕ�������
�@�����̎��A�`�L�o�L��4�{�̒����ƌ���邱�Ƃɒ��ӂ���
�@�@���̍ہA�i�q�_�i���O�p�`�̒��_�j�ɂ����Ă�1�{�̒����ƌ������̂Ƃ݂Ȃ�
�����1�ӂ̒�����30�ł��鐳�O�p�`�`�a�b�ɂ����Ă�
4�~10=40�̏��O�p�`��2�̕����ɕ�������
�i3�j�`�i0�A15��3�j�A�a�i0�A0�j�A�b�i30�A0�j�Ƃ��A
�i3�A0�j���u�A�i4�A0�j���v�A�i7/2�A��3/2�j���w�A�i9/2�A��3/2�j���x�Ƃ���
�q�r�̏ꍇ�ɂ��čl����
�@�T�@�X����-��3�̒����Ƃq�r
�@�@�@�q�r�́i4�A0�j�A�i5�A0�j�A�i6�A0�j�A�E�E�E�E�A�i29�A0�j�A�i30�A0�j��ʂ钼���ƌ����E�E�E�E27�{�ƌ����
�@�U�@�X������3�̒����Ƃq�r
�@�@�@�b�`��ɓ_�s���b�s=4�ƂȂ�悤�ɂƂ�� �s��ʂ�X����3�̒����́i26�A0�j��ʂ邩��A
�@�@�@�q�r�́i4�A0�j�A�i5�A0�j�A�i6�A0�j�A�E�E�E�E�A�i25�A0�j�A�i26�A0�j��ʂ钼���ƌ����E�E�E�E23�{�ƌ����
�@�V�@�X����0�̒����Ƃq�r
�@�@�@�q�r��y=��3/2�A��3�A3��/2�ƌ����E�E�E�E3�{�ƌ����
���킹��53�{�̒����ƌ����
�i�q�r������钼���̐��j=�i�q�r���ʂ鏬�O�p�`�̐��j������A�q�r��53�̏��O�p�`��ʂ�
�@�W�@�d���ɂ��Ă̌���
�@�@�@�q�ߕӂɂ��čl����
�@�@�@�@�@�P�j�p�q�A�q�r�Ƃ��Ɂ��w�u�v��ʂ�
�@�@�@�@�@�Q�j�p�q���ӂw�v�ƌ����Ȃ�p�q�A�q�r�Ƃ��Ɂ��w�v�x��ʂ�
�@�@�@�q�w�̉����Ƃ`�a�Ƃ̌�_��x���W��1111/222=5.0045�E�E�E�A
�@�@�@�p��x���W�� 15-1.6665=13.3335 ������
�@�@�@�p�q�͕ӂw�v�ƌ����
�@�@�@����Ăq�̋ߕӂɂ����Ă͂p�q�Ƃq�r���Ƃ��ɒʂ鏬�O�p�`��2���邱�ƂɂȂ�
�@�p�q�A�r�p�Ƃ���53�̏��O�p�`��ʂ�
�@�p�ߕӁA�r�ߕӂł�������2�{�ʂ鏬�O�p�`��2���邩��
�@�p�q�A�q�r�A�r�p���ʂ鏬�O�p�`�͑S���Ł@�i53-2�j�~3=153��
���p�q�A�q�r�A�r�p�Ƃ��i�q�_��ʂ�Ȃ����A����ɂ��Ă̐����͏ȗ�����
�i4�j�`���܂ޏ��O�p�`�𔒁A����Ɨׂ肠���������̏��O�p�`�����A
���̍��E�𔒂Ƃ����悤�Ɏs���͗l�ɓh�蕪�����
�@�@���͑S����1�{2�{3�{�E�E�E�E�{30=465
�@�@���͑S����1�{2�{3�{�E�E�E�E�{29=435
����āi���j�����Ȃ��Ƃ�465-435=30���K�v
�E����8
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
(1) ��i����P�C�Q�C�R�A�E�E�E�Q�X�C�R�O�ƂP�C�Q�C�R�A�E�E�E�Q�W�C�Q�X��
�̐��O�p�`������܂��̂ō��v���܂��B
�i�P�{�R�O�j�~�R�O���Q�{�i�P�{�Q�X�j�~�Q�X���Q���P�T�~�U�O���X�O�O�ł��B
(2) �a�b���R�O�a�o���P�O�ł���B���̔䗦�Œʂ钼���͂R�i�ڂ̍�������P�Ԗڂ�ʂ�܂��B
�U�i�ڂ̍�������Q�Ԗڂ�ʂ�܂��B�����Ȃ�ƂQ�ɕ������鐳�O�p�`�͂R�i������S�ƕ�����܂��B
������v�Z���܂��B
�R�O���R�~�S���S�O�ł��B
(3)�i�����p�q������ӂ`�b�ƕ��s�Ȓ����{�ӂ`�a�ƕ��s�Ȓ����{�ӂ`�b�ɕ��s�Ȓ����\�i�d���������O�p�`�̐��j�~�R�Ōv�Z���܂��B
���̐}�͂T�i�ڂ܂ł̐}�ʼn��F���������d�����Đ����܂��̂ō��������܂��B
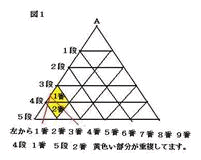
�Q�U�{�Q�U�{�R�|�Q���T�R�ɂȂ�܂��B
�R�ӂ���܂��̂łR�{���܂��B����ƂR�����̂Q���_�u���v�Z�ɂȂ�܂��̂�
���̕��������܂��B
�T�R�~�R�|�i�R�~�Q�j���P�T�R
(4) ���̃^�C���͍ŏI�i�̐������g�p���܂��̂łR�O�i�ŏI���܂��̂łR�O���g�p�ƂȂ�܂��B
�E����9
�i�y���l�|���F�]�ʔ����j
(�P)
�����O�p�`�Ɛ��O�p�`�`�a�b�̑�����͂P�F�R�O�Ȃ̂�
�����̖ʐϔ�́A�P�F�X�O�O
�������O�p�`�̐��͂X�O�O
(�Q)
���O�p�`�`�a�b�̒��_�`����R�i�ڂ܂ł̐��O�p�`�`�c�d���l����B
���O�p�`�`�c�d�Ɛ��O�p�`�`�a�b�̑�����͂P�F�P�O�Ȃ̂�
�����`�o�́A�ӂc�d��̓_�łc�p���P�����_�p��ʂ�B
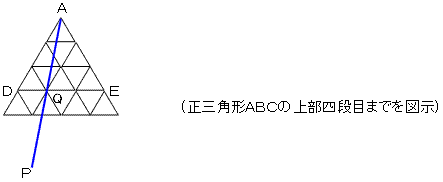
���āA���O�p�`�`�c�d�ɂ��āA�����`�o�ɂ���ē�̕����ɕ������鏬���O�p�`�͂S����B
�����O�p�`�`�a�b�ɂ��ẮA�S�~�P�O���S�O
(�R)
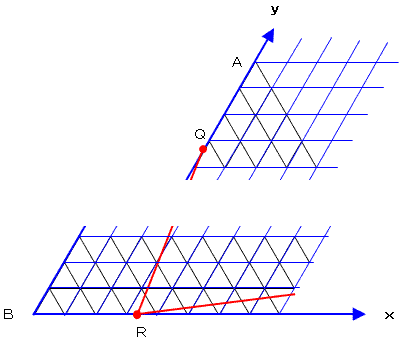 ���߂鏬���O�p�`�̐��́A�O�p�`�p�q�r�̎��������O�p�`�̒��_��ʉ߂��邩�ǂ����ɂ���Č��܂�B
���߂鏬���O�p�`�̐��́A�O�p�`�p�q�r�̎��������O�p�`�̒��_��ʉ߂��邩�ǂ����ɂ���Č��܂�B
���L�̂悤�Ȕ����W�n���Ƃ�ƁA���̌�_�͏����O�p�`�̒��_�ƈ�v���A
�����p�q�̎��́A�����|�i�Q�U�D�U�U�V�^�R�D�R�R�R�jx�{�Q�U�D�U�U�V
�@�@�@X=1�@�@y��18.7
�@�@�@X=2�@�@y��10.7
�@�@�@X=3�@�@y��2.7
����āA�����p�q�͐��O�p�`�`�a�b�̏㕔�S�i�ڂ���R�O�i�܂ł�ʉ߂���Ƃ��A
�S�i�ڂɂ��ẮA�ЂƂ̏����O�p�`��ʉ߂��A
�T�i�ڂ���R�O�i�ɂ��ẮA��i�ɂ��ē�̏����O�p�`�����邽�߁A
�����p�q�ɂ��đ�ӂ��������O�p�`�̐��́A
�@�@�i�R�O�|�S�j�~�Q�{�P���T�R�B
�����q�r�A�r�p�ɂ��Ă��A���̑��ΓI�Ȉʒu�W�͒����p�q�Ɠ����ł��邱�Ƃ���A
��ӂ��������O�p�`�̐��͉�����T�R�B
�A���A���_�p�A�q�A�r�ߖT�Ŋe�Q���d�����Đ����Ă��邽�߁A
�@�@�T�R�~�R�|�U���P�T�R
���O�p�`�p�q�r�ɂ��ĂP�T�R
�����P�C�Q�C�R�ɑ��āAy�͐����l�����Ȃ��̂ŁA�����p�q�͏����O�p�`�̉���̒��_���ʂ�Ȃ��B
����āA�����p�q�͐��O�p�`�`�a�b�̏㕔�S�i�ڂ���R�O�i�܂ł�ʉ߂���Ƃ��A
�S�i�ڂɂ��ẮA�ЂƂ̏����O�p�`��ʉ߂��A
�T�i�ڂ���R�O�i�ɂ��ẮA��i�ɂ��ē�̏����O�p�`�����邽�߁A
�����p�q�ɂ��đ�ӂ��������O�p�`�̐��́A�i�R�O�|�S�j�~�Q�{�P���T�R�B
�����q�r�A�r�p�ɂ��Ă��A���̑��ΓI�Ȉʒu�͒����p�q�Ɠ����ł��邱�Ƃ���A
��ӂ��������O�p�`�̐��͉�����T�R�B
�A���A���_�p�A�q�A�r�ŏd�����Đ����Ă��邱�Ƃ��l�����āA�T�R�~�R�|�R���P�T�U
���O�p�`�p�q�r�ɂ��Ă͂P�T�U
(�S)
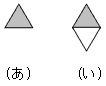
���O�p�`�`�a�b���ȉ��̂悤�ɐF��������ƁA
�@�@���̏����O�p�`�́A�i�P�{�R�O�j�~�P�T���S�U�T��
�@�@���̏����O�p�`�́A�@�@�X�O�O�|�S�U�T���S�R�T��

���āA(��)�̃^�C���Ő��O�p�`�`�a�b�����Ƃ��ł���Ƃ���ƁA
���Ɣ��̃^�C���͓����ƂȂ�͂��ł���B
�Ƃ��낪�A�����S�U�T�|�S�R�T���R�O�������̂ŁA(��)�̃^�C���͂R�O���K�v�ƂȂ�B
�����Ȃ��Ƃ��R�O��
�E����10
�i�y���l�|���Fhaya�j
(1) �S����900�̏��O�p�`�ɕ������
(2) ����AP�ɂ����2�̕����ɕ������鏬�O�p�`�̐���40��
(3) �O�p�`QRS�̎����ʂ鏬�O�p�`�̐���153��
(4) �K�v��(��)�̃^�C������30��
�y�������z
(1)�@�@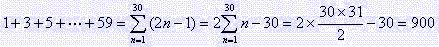
(2)�@����(4)��(��)�̃^�C�����E�ߏ�ɂ�����q�������s�l�ӌ`��P�ʂƂ��āA��ԏ�̓_��
���̓_�����Ԑ}�`���R�i�ږ��ɌJ��Ԃ���A���ꂼ��S�̎O�p�`�������Ă��邩��A
�@�@4x30/3=4x10=40
(3)�@��}����ƁA�O�ӂ͂ǂ̏��O�p�`�̒��_�Ƃ�����炸��ӂɂ�53�̏��O�p�`�ɊW���Ă���B
�P����3�{����ƁA���_�̂��鏬�O�p�`�ƒ��߂̏��O�p�`��2�d�ɐ������邱�ƂɂȂ�̂ł�������āA
�@�@53x3-2x3=153
(4)�@�ォ�珇�Ɂu���v�Ō��ԂȂ��~���l�߂邱�Ƃ��ł��邪�A
�ʼn��i�̐����̏��O�p�`30�̂݁u���v���g���K�v�����邩��A30��
�E����11
�i�y���l�|���Ffalcon@���w���t�j
��������
�i�P�j�X�O�O��
�i�Q�j�S�O��
�i�R�j�P�T�R��
�i�S�j�R�O��
���l������
�i�P�j��̒i����1�A�R�A�T�E�E�E�Ƒ����Ă����܂��B
30�i�ڂɂ͎O�p�`�̌����T�X�ɂȂ�̂ł����S�đ������킹��ƂX�O�O�ƂȂ�܂��B
�i�Q�j�����`�o��3�i���Ƃɏ��O�p�`�̒��_��ʉ߂��܂��B
����3�i�̊ԂɂQ�̕����ɕ������鏬�O�p�`�͂S����܂��B
�S�̂ł͂R�O�i�Ȃ̂ł��̂���Ԃ����P�O��ƍl���āA
�Q�̕����ɕ������鏬�O�p�`��10�~�S���S�O�ƂȂ�܂��B
�i�R�j�O�p�`�p�q�r�̊e�ӂ͏��O�p�`���P�{�Q�~�Q�U���T�R�ʂ�܂��B
�P���ɎO�p�`�p�q�r�̕ӂ̐�����R�{���ĂP�T�X�B
����ł͒[�X�ŏd�����Đ����Ă��܂����O�p�`���Q������̂ŁA���̂Ԃ�������ĂP�T�R�B
�i�S�j���낢��Ȃ����ōl���Ă݂͂܂������A�R�O����菭�Ȃ������v�����Ȃ������ł��B
�E����12
�i�y���l�|���Fteki�j
����
�P�@�@�X�O�O��
�Q�@�@�@�S�O��
�R�@�@�P�T�R��
�S�@�@�@�R�O��
����@��
�P�@�R�O�i����̂łR�O�Q���X�O�O�B�i�ʉ��Ƃ��āA�ʐς��X�O�O�{�ɂȂ�̂łX�O�O�B�j
�Q�@�R�i�̐��O�p�`���l����A�S����������A�i�q�_��ʂ�̂ŁA4/3�~�R�O���S�O�B
�R�@�^����ꂽ���l�����r���[�i3/10�ł�1/3�ł��Ȃ��j�Ȃ̂ŁA�����炭
�����p�q�A�q�r�A�p�r��Ɋi�q�_�͂Ȃ����낤�Ǝv���܂������A����
�ł����A�Y��ł܂���(^^;;
�@�ŁA�d���Ȃ��w���@�ɂ��������ŏؖ����邱�Ƃɂ��܂����B
�@�����p�q��Ɋi�q�_������Ɖ��肵�A������s�Ƃ���ƁA�`�a��ɂa�b��
�t�s�����s�ɂȂ�悤�ȓ_�t�����ƁA�_�t���i�q�_�ɂȂ�܂��B
�@�`�t�����A�t�s�����Ƃ����ƁA�O�p�`�̑�������A�ȉ��̎����������܂��B
�@�Q�U�D�U�U�V���R�D�R�R�R���i���|�R�D�R�R�R�j����
�@�ό`���āA�R�D�R�R�R���|�Q�U�D�U�U�V�����R�D�R�R�R�Q
�@���A���͐����Ȃ̂ŁA����͖����ł��B
�@����āA�p�q��Ɋi�q�_�͂���܂���B
�@�q�r�A�p�r������l�Ɋi�q�_�͂���܂���B
�@���āA�����p�q�Ƃ`�a�A�a�b�A�b�`�ɕ��s�Ȑ����Ƃ̌�_�̐��́A���ꂼ��
�R�A�Q�U�A�Q�R�ō��v�T�Q�ł��̂ŁA
�p�q�ɕ��������O�p�`�̐��͂T�Q�{�P���T�R�ł��B
�@�q�r�A�p�r�����l�ɂT�R�̎O�p�`�����܂����A���ꂼ��̒��_�t��
�ł́A�Q�̐����ɂ���ĕ��������O�p�`���Q������܂��B
�@����đ�ӂ̌��́A�T�P�~�R���P�T�R�B
�S�@�ʼn��i���i���j�̐}�`�Ŗ��߂Ă��܂��A��́i���j�̐}�`�Ŗ��߂邱�Ƃ��ł���
�@�@�̂łR�O�B�i�s���͗l�ɖ��߂Ă��܂��A���ꂪ�ŏ��ł��邱�Ƃ��킩��܂��B�j
�E����13
�i�y���l�|���FSOU�j
x������y���������̎ΕӂƂ��Č��܂��B
(1)
�O�p�`�̖ʐς�450 �Ȃ̂ŁA�ʐ�1/2 �̎O�p�`�� 900//
(2)
����AP �̕�������
�@�@�@y=-3x+30
�ŁA�i�q�_��ʂ�B�i�q�_����y��3������4�̎O�p�`�f����̂� 40//
�@
(3)
����QR �̕�������
�@�@�@y = -(26.667/3.333)x + 26.667
�ƂȂ邪����͂��̎O�p�`�̒��Ő������������Ȃ��̂ŁA
y��1�����x�ɕK��2�̎O�p�`�f����B�]����QR��
�@�@�@26*2 + 1 = 53
�̎O�p�`��ʂ�B�܂��A���_�t�߂�2�̒�����2�̎O�p�`��
���L���Ă��葼��2�{�̒����̕��Əd�Ȃ�̂ŁA
�@�@�@53*3 - 2*3 = 153 //
(4)
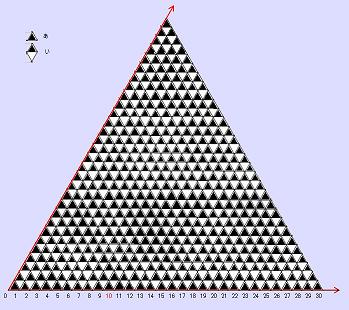
�������Ƃ��āA���ƐF����B(��)�̐}�`�͂���2�̎O�p�`���g�ɂȂ��Ă���B
���́�����30�����̂ŁA�ǂ�Ȏ��������Ă��A���Ȃ��Ƃ�30�́��̓y�A����ꂸ�]��B//
�E����14
�i�y���l�|���F��ӂ����̂炢��������j
�i�P�j
�����̊W�ɂ���}�`�̖ʐς͑Ή����钷����2��ɔ�Ⴕ�܂��B
��ӂ̒�����1�̏��O�p�`�̖ʐς���Ƃ���ƈ�ӂ�30�̑�O�p�`�̖ʐς́A302=900 �{�ł��B
����āA���O�p�`��900����܂��B
�i�Q�j
AB�FBP��3�F1�Ȃ̂�AP�͉E�̐}�̂悤�ɂȂ��Ă��܂��B
�ォ��3�i�ڂ܂ł�2�̕����ɕ������鏬���O�p�`��4����܂��B
�����4�~10��40�ł��B
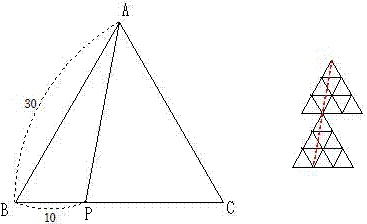
�i�R�j
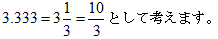
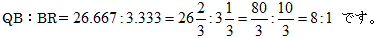
���O�p�`�̒�ӂ̍��[���牺��8���O�p�`�������ɉ������ӂ̉E�[�����Ԑ��������܂��B
�P������������ɂ��ӂ�1�^8(��0.125)�������Ă����܂��B�i�Ԃŕ\���j
�_Q�����鏬�O�p�`�ɂ�����QR����ӂ̂ǂ̈ʒu�����邩�ׂ܂��B
����ƁA��ӂ̍�����
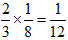 �̂Ƃ�������邱�Ƃ��킩��܂��B
�̂Ƃ�������邱�Ƃ��킩��܂��B
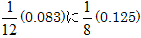 �����������Ă������ɂ͂Ȃ�܂���B
�����������Ă������ɂ͂Ȃ�܂���B
����QR��������1�{����Ə��O�p�`2��ʂ邱�ƂɂȂ�܂��B
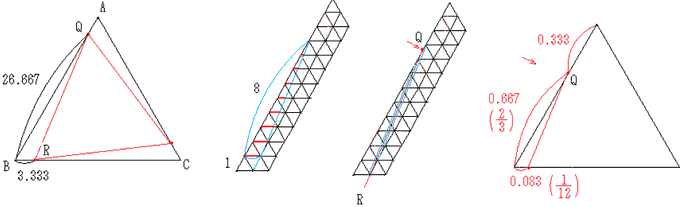
Q���܂ޏ��O�p�`�͏ォ��4�ڂ߂̉�������ӂɂȂ�Ƃ���ɂ���܂��B
��������29�ڂ̉�������ӂɂȂ鏬�O�p�`�܂ʼn�����29�|4�{1��26�{����܂��B
�����QR�����鏬�O�p�`��2�~26�{1��53����܂��B
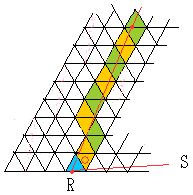
����QR���l���܂����A�}�̐̏��O�p�`���ԁ����������O�p�`���d�Ȃ��Ă��܂��B
����āA�O�p�`QRS�����鏬�O�p�`��3�~(53�|2)��153�ɂȂ�܂��B
�i�S�j
�ォ��H�^�Ō��ԂȂ������Ă����ƈ�ԉ��̂Ƃ����30�̏��O�p�`���c��܂��B
�ʼn��i�̍��[�̏��O�p�`��H�^�ŕ����Ɖ�����2�i�ڂ̂Ƃ���Ŕ��[�̏��O�p�`���ł��܂��B
���[�ȏ��O�p�`�𑼂̏��O�p�`�ƂȂ��ĕH�^������Ƃ��܂܂ŕH�^����������������Ă��܂��܂��B
���̔��[�ȏ��O�p�`���Ȃ��邱�Ƃ��ł��Ȃ��̂�30�̏��O�p�`�����炷���Ƃ��ł��܂���B
�i���j�̏��O�p�`��30�K�p�ł��B
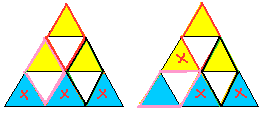
�E����15
�i�y���l�|���F���q�̗Y�L�j
(1)������̎O�p�`��1,2,3,4, ..... ,29,30��
�@�������̎O�p�`��0,1,2,3,4, ..... ,29��
�������̎O�p�`���t���琔���� 29,28,27,26, .... , 1, 0���A
������̎O�p�`�� 1, 2, 3, 4, .... ,29,30���B
�㉺��������30,30,30,30,30 ...... �����v30�g�B
�����30*30=900���B
(2)���_�`���Ƃ���A�ӂa�b��́A�a�o���P�O�ƂȂ�_�o���Ƃ���̂�����A
�R�i���~��邲�Ƃɕӂ`�a����P�����i�����𐅕��Ɍv��Ɓj����Ă������Ƃ�
�Ȃ�B
����āA�R�i���~��邲�Ƃɏ��ɂP�C�Q�C�P�̏����O�p�`��ʂ�̂ŁA���v
�S�O�B
(3)�S�i�ڂ̓r������R�O�i�ڂ܂Ő����Ƃ���A�T�i�ڂ���Q�X�i�ڂ܂ł͂Q��
�̏��O�p�`��ʂ�̂ŁA�T�O���R�{�R�łP�T�R�B
�O�p�`�p�q�r���A���_��ʂ�Ȃ��Ƃ����ؖ�
�ӂ`�a���x���A�ӂa�b���w���A�_�a�����_�ƂȂ�悤�ɍ��W�ϊ�����B
�_�p�̍��W�́@(x,y)=(0,30-3.333)=(0,26.667)
�_�q�̍��W�́@(x,y)=(3.333,0)
�_�r�̍��W�͕ӂ`�b��AS:SC=26.667:3.333�ɓ�������_�ł��邩��@(x,y)=(26.667,3.333)
�����p�q�̕������� ���� -8.000900090009 x + 26.667
�����q�r�̕������� ���� 0.14283877603497 x +-0.47608164052456
�����r�p�̕������� ���� -0.87501406232422 x + 26.667
�ǂ̕��������A�����Ȃ��Ƃ�0��x��30�͈͓̔��ł�x,y���Ƃ��ɐ����ƂȂ������
���Ȃ��B���̐}�ł������O�p�`�̒��_�́A���W�ϊ����x,y���Ƃ��ɐ����ƂȂ�
�_�ɂȂ�̂ŁA�����p�q�A�����q�r�A�����r�p�͂Ƃ��ɁA���̐}�ł������O�p�`
�̒��_��ʂ邱�Ƃ͖����B
(4)�@�^�C���i���j��p����Ɩ��(1)�Ő�����������̎O�p�`�Ɖ������̎O�p�`
�Ƃ𗼕��������ƂɂȂ�B
����Ă��̍��Ɠ���30�̃^�C���i���j���K�v�ƂȂ�B
������
| teki | �X���[�N�}�� | haya |
| T_Tatekawa | ���q�̗Y�L | falcon@���w���t |
| �̂����� | �]�ʔ��� | ��ӂ����̂炢�������� |
| Ryu1128 | ��̂������� | SOU |
| �I���W | ������͑��� | �o���^�����l |
�R�����g
���ɍ���́A(3)����������ł��ˁB���_�̋߂��ŁA�O�p�`�p�q�r�����O�p�`���Q��ʂ�ꍇ������܂��̂ŁA
�d�����l�����Ȃ���Ȃ�܂���B
�܂��A�O�p�`�p�q�r�����_��ʂ�Ȃ��Ƃ������Ƃ��m�F����K�v������܂��ˁB
 top
top