Challenge!

問題169　２０１１年の問題
Weekend Mathematics／問題／問題169　２０１１年の問題

問題169　２０１１年の問題

[x] は、x を超えない最大の整数を表すとき、次の式を計算してください。



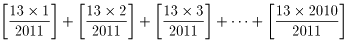
問題の出典

広中杯　ハイレベル中学数学に挑戦
講談社
2001年トライヤル問題 改題

解答

解答・その1

（ペンネ－ム：エルドス）

ＢＡＳＩＣで組んでみましたが、１２０６０のようです。

   
CLEAR
FOR i=1 TO 2010
   LET x=INT(13*i/2011)
   LET s=s+x
NEXT i
PRINT s
END


解答・その2

（ペンネ－ム：浜田　明巳）

この問題をプログラムで解いたならば，面白さが半減する事は分かっているのですが，ついつい解いてしまいました．
エクセルのマクロです．答は１２０６０でした．

  Option Explicit
Sub Macro1()
    Range("A1").Select
    Cells(1, 1).Value = "=INT(13*ROW()/2011)"
    Selection.AutoFill Destination:=Range("A1:A2010"), Type:=xlFillDefault
    Range("A1:A2010").Select
    Cells(1, 2).Value = "=SUM(A1:A2010)"
    Range("B1").Select
End Sub
Sub Macro2()
    Dim kotae As Integer
    Dim j As Integer
    kotae = 0
    For j = 1 To 2010
      kotae = kotae + Int(13 * j / 2011)
    Next j
    MsgBox (Str(kotae))
End Sub


解答・その3

（ペンネ－ム：転位反応）

Ｎn＝１３ｎ／２０１１とおく。
Ｎ2010について、12≦13×2010／2011＜13 なので、［Ｎ2010］=12
よって、n=1～2010について、1～12の各整数値を取るＮnの個数を数え上げれば良い。
以下に、n=Ｎn×2011/13から逆算してnを求めた後、表1に結果を整理した。
なお、ｎ(逆算値）が割り切れない場合は小数第一位まで表示。



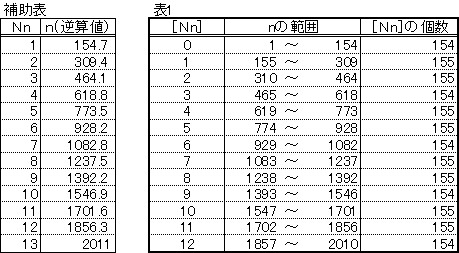
よって、
　　　　［Ｎ1］＋・・・＋ ［Ｎ2010］
　　　　=155×(1+2+4+5+7+8+10+11)+154×(3+6+9+12)
　　　　=155×(1+2+3+4+5+6+7+8+9+10+11+12)-(155-154)×(3+6+9+12)
　　　　=155×78-30
　　　　=12060

解答・その4

（ペンネ－ム：のっこん）

2011/13＝154＋（9/13）　　これを a とおく

１）分子が13・1～13・154の時は値が0
２）2a＝309＋（5/13）だから分子が13・155～13・309の時は値が1（個数は155）
３）3a＝464＋（1/13）だから　　〃　13・310～13・464の時は値が2（　〃　　155）
４）4a＝618＋（10/13）だから　　〃　13・465～13・618の時は値が3（　〃　　154）
５）5a＝773＋（6/13）だから　　〃　13・619～13・773の時は値が4（　〃　　155）
６）6a＝928＋（2/13）だから　　〃　13・774～13・928の時は値が5（　〃　　155）
７）7a＝1082＋（11/13）だから　　〃　13・929～13・1082の時は値が6（　〃　154）
８）8a＝1237＋（7/13）だから　　〃　13・1083～13・1237の時は値が7（　〃　155）
９）9a＝1392＋（3/13）だから　　〃　13・1238～13・1392の時は値が8（　〃　155）
１０）10a＝1546＋（12/13）だから　　〃　13・1393～13・1546の時は値が9（　〃　154）
１１）11a＝1701＋（8/13）だから　　〃　　13・1547～13・1701の時は値が10（　〃　155）
１２）12a＝1856＋（4/13）だから　　〃　　13・1702～13・1856の時は値が11（　〃　155）
１３）13a＝2011だから　　　　　　　　〃　　13・1857～13・2010の時は値が12（　〃　154）

与式＝155（1＋2＋4＋5＋7＋8＋10＋11）＋154（3＋6＋9＋12）
　　＝155・48＋154・30
　　＝7440＋4620
　　＝12060

解答・その5

（ペンネ－ム：オヤジ）



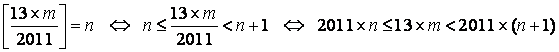
但し　ｍ，ｎ　は、整数　　ｍ＝１～２０１０、ｎ＝０～１２　
ｎの値によって場合分けする

（１）ｎ＝１のとき　２０１１×１≦１３×ｍ＜２０１１×２　を解くと
　　　　　　　　ｍ＝　１５５　～　３０９　：１５５個

（２）ｎ＝２のとき　２０１１×２≦１３×ｍ＜２０１１×３　を解くと
　　　　　　　　ｍ＝　３１０　～　４６４　：１５５個

（３）ｎ＝３のとき　２０１１×３≦１３×ｍ＜２０１１×４　を解くと
　　　　　　　　ｍ＝　４６５　～　６１８　：１５４個

（４）ｎ＝４のとき　２０１１×４≦１３×ｍ＜２０１１×５　を解くと
　　　　　　　　ｍ＝　６１９　～　７７３　：１５５個

（５）ｎ＝５のとき　２０１１×５≦１３×ｍ＜２０１１×６　を解くと
　　　　　　　　ｍ＝　７７４　～　９２８　：１５５個

（６）ｎ＝６のとき　２０１１×６≦１３×ｍ＜２０１１×７　を解くと
　　　　　　　　ｍ＝　９２９　～　１０８２　：１５４個

（７）ｎ＝７のとき　２０１１×７≦１３×ｍ＜２０１１×８　を解くと
　　　　　　　　ｍ＝　１０８３　～　１２３７　：１５５個

（８）ｎ＝８のとき　２０１１×８≦１３×ｍ＜２０１１×９　を解くと
　　　　　　　　ｍ＝　１２３８　～　１３９２　：１５５個

（９）ｎ＝９のとき　２０１１×９≦１３×ｍ＜２０１１×１０　を解くと
　　　　　　　　ｍ＝　１３９３　～　１５４６　：１５４個

（１０）ｎ＝１０のとき　２０１１×１０≦１３×ｍ＜２０１１×１１　を解くと
　　　　　　　　ｍ＝　１５４７　～　１７０１　：１５５個

（１１）ｎ＝１１のとき　２０１１×１１≦１３×ｍ＜２０１１×１２　を解くと
　　　　　　　　ｍ＝　１７０２　～　１８５６　：１５５個

（１２）ｎ＝１２のとき　２０１１×１２≦１３×ｍ＜２０１１×１３　を解くと
　　　　　　　　ｍ＝　１８５７　～　２０１０　：１５４個

（１）～（１２）より
　１×１５５＋２×１５５＋３×１５４＋４×１５５＋５×１５５＋６×１５４
　＋７×１５５＋８×１５５＋９×１５４＋１０×１５５＋１１×１５５＋１２×１５４
＝　１２０６０

　∴　１２０６０

解答・その6

（ペンネ－ム：迷子の雄猫）

解けはしましたが、すっきりとしませんね。 もう少しエレガントに解けるかと思ったのですが、 その方法が見当もつきません。

[13 * 154 / 2011]=0
[13 * 155 / 2011]=1
[13 * 309 / 2011]=1より1が155個、小計155
[13 * 310 / 2011]=2
[13 * 464 / 2011]=2より2が155個、小計310
[13 * 465 / 2011]=3
[13 * 618 / 2011]=3より3が154個、小計462
[13 * 619 / 2011]=4
[13 * 773 / 2011]=4より4が155個、小計620
[13 * 774 / 2011]=5
[13 * 928 / 2011]=5より5が155個、小計775
[13 * 929 / 2011]=6
[13 * 1082 / 2011]=6より6が154個、小計924
[13 * 1083 / 2011]=7
[13 * 1237 / 2011]=7より7が155個、小計1085
[13 * 1238 / 2011]=8
[13 * 1392 / 2011]=8より8が155個、小計1240
[13 * 1393 / 2011]=9
[13 * 1546 / 2011]=9より9が154個、小計1386
[13 * 1547 / 2011]=10
[13 * 1701 / 2011]=10より10が155個、小計1550
[13 * 1702 / 2011]=11
[13 * 1856 / 2011]=11より11が155個、小計1705
[13 * 1857 / 2011]=12
[13 * 2010 / 2011]=12より12が154個、小計1848
合計12060

解答・その7

（ペンネ－ム：ykak）

答え　　１２，０６０

考え方
これは１個ずつ計算するしか方法がないように思いますが。
問題の式の各項を１３×n／２０１１という形で書くと、 答えは、nが１から２０１０までの項の和ということになる。
[１３×n／２０１１]が１になるためには、１３×A／２０１１＝１とすると、
A＝１×２０１１／１３で、Aは１５４．６９２・・・となるから、nは１５５以上でなければならず、
nが１５４以下なら[１３×n／２０１１]は０である。

同じようにして、[１３×n／２０１１]が２になるためには、
１３×A／２０１１＝２とすると、A＝２×２０１１／１３で、Aは３０９．３８４・・・となるから、
ｎは３１０以上でなければならず、nが３０９以下なら[１３×n／２０１１]は１である。
以下nが２０１０になるまで同様の計算をすれば問題の答えが求められるが、
[１３×n／２０１１]が１３の時、上記のAに該当する数を求めると、１３×２０１１／１３で、 ちょうど割り切れて２０１１になるので、
nが２０１０の項は、[１３×n／２０１１]が１２になる場合の最大の項ということになる。

nの値が３以上の場合も、２までの場合と同様に計算して表にする。



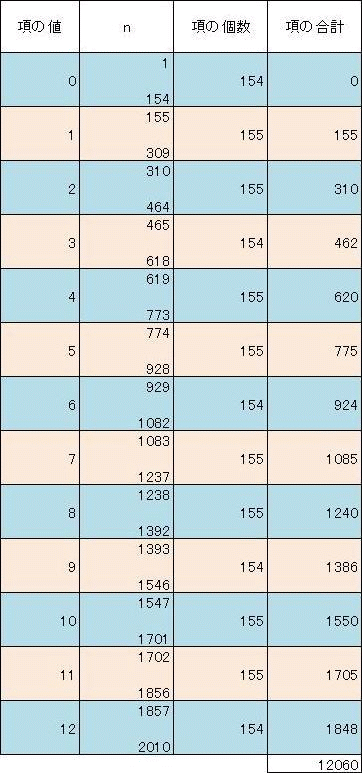
表の一番左の列は各項の値で、０から１２まである。
次の列（ｎ）は、１列目の項の値を取る各項のうちnが最小になる場合と最大になる場合の値を表す。
たとえば、項の値が３の場合、表のｎの列の４行目（表題部を除く）の上の４６５がnが最小になるときの値であり、下の６１８がｎが最大になるときの値である。
表の３列目（項の個数）は、各項の値を取る項の個数を表す。
たとえば、項の値が５である項の数は、３列目の６行目にある１５５である。
また、４列目（項の合計）は、各項の値を取る項全部の合計を表す。
従って問題の答えは、これをすべて加えた１２，０６０になる。

解答・その8

（ペンネ－ム：T_Tatekawa）

2011 を 13 で割ることを考える．
　　　2011 = 154 x 13 + 9
よって最初から 154 項目までは 0． 155 項目から 1 になる．次に
　　　2011 x 2 = 4022 = 309 x 13 + 5
なので，310 項目までは 1． 311 項目から 2 になる．

このようにして，2011の倍数を 13 で割った時の商と余りを考えると，
　　　2011 x 3 = 6033 = 464 x 13 + 1
　　　2011 x 4 = 8044 = 618 x 13 + 10
　　　2011 x 5 = 10055 = 773 x 13 + 6
　　　2011 x 6 = 12066 = 928 x 13 + 2
　　　2011 x 7 = 14077 = 1082 x 13 + 11
　　　2011 x 8 = 16088 = 1237 x 13 + 7
　　　2011 x 9 = 19099 = 1392 x 13 + 3
　　　2011 x 10 = 20110 = 1546 x 13 + 12
　　　2011 x 11 = 22121 = 1701 x 13 + 8
　　　2011 x 12 = 24132 = 1856 x 13 + 4

となり，0, 3, 6, 9, 12 の項が 154個．
1, 2, 4, 5, 7, 8, 10, 11 の項が 155個．
0 から 12 までの総和は
　　　 (0+12)*13/2 = 78
よって求める値は
　　　78 x 155 - (3+6+9+12) = 12060

解答・その9

（ペンネ－ム：夜ふかしのつらいおじさん）

まず2011の倍数を、13×2010＝26130を超えるまで計算します。
最後の数は、26130に置き換えます。

次にその数を13で割って商を求めます。
(余りはこの問題では重要ではありません)
最初の商の154は、［13×k／2011］＝0となるものの個数です。
次の商の309から最初の商の154を引いた数155は、［13×k／2011］＝1となるものの個数です。

以下同様に個数を数えます。 次に、［13×k／2011］の値とその個数を掛けます。
最後にその総和を求めます。



解答・その10

（ペンネ－ム：falcon@中学教師）

＜答え＞ 12060

＜考え方＞
与式の項をa(1)、a(2)、a(3)・・・と表記すると、
・a(1) ～ a(154) → ０
・a(155) ～ a(309) → 1
・a(310) ～ a(464) → 2
・a(465) ～ a(618) → 3
・a(619) ～ a(773) → 4
・a(774) ～ a(928) → 5
・a(929) ～ a(1082) → 6
・a(1083) ～ a(1237) → 7
・a(1238) ～ a(1392) → 8
・a(1393) ～ a(1546) → 9
・a(1547) ～ a(1701) → 10
・a(1702) ～ a(1856) → 11
・a(1857) ～ a(2010) → 12

となるので、
与式＝ 1×155＋２×155＋３×154＋４×155＋５×155＋６×154
　　　　　＋７×155＋８×155＋９×154＋10×155＋11×155＋12×154
　　＝ 155 + 310 + 462 + 620 + 775 + 924 + 1085 + 1240 + 1386 + 1550 + 1705 + 1848
　　＝ 12060

解答・その11

（ペンネ－ム：杖のおじさん）

答え　１２０６０　です。

解　１

今回はCASIO FX－870P　の　ポケコンを使いプログラムを作って計算しました。

１０　Ａ＝０：ＰＲＩＮＴ“スタート”
２０　ＦＯＲ　Ｂ＝１　ＴＯ　２０１０
３０　Ｃ＝ＩＮＴ（１３＊Ｂ／２０１１）
５０  Ａ＝Ａ＋Ｃ
６０　ＮＥＸＴ　Ｂ
７０　ＢＥＥＰ：ＰＲＩＮＴ“コタエ　ハ　”；Ａ
８０　ＩＦ　ＩＮＫＥＹ＄＝“”ＴＨＥＮ　８０
９０　ＧＯＴＯ　１０　

実行しますと１分３２秒でピ！と音が出て　コタエ　ハ　１２０６０　と表示されます。
８０行でループして停止しています。ＥＸＥキーを押すと１０行に戻ります。

解　２

１番目と２０１０番目を加算する。次に２番目と２００９番目を加算する。
それぞれの加算は同じ数字になります。 従って

　　(１３×１)＋(１３×２０１０)÷２０１１＝１３

組み合わせは２０１０÷２＝１００５組なので １３×１００５＝１３０６５になりなすが各項を別々に計算すると０＋１２＝１２となります。
すべての組み合わせは同じなのです。各項共に１３未満になりそれを超えない整数は１２になります。 従って 答えは
　　１３０６５－（１×１００５）＝１２０６０となります。

解答・その12

（ペンネ－ム：haya）

求める式の値は 12060 です。

【解き方】
和の式の各項は 0～12 まで単調に増加する。　仮に値が 1 となる範囲 x, y を求めると



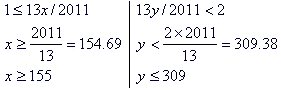
値は 154 ないし 155 の間隔で変化するとして、下表を完成させて合計値を求めると 12060 となる。

ValueFromToNumVxN
011541540
1155309155155
2310464155310
3465618154462
4619773155620
5774928155775
69291082154924
7108312371551085
8123813921551240
9139315461541386
10154717011551550
11170218561551705
12185720101541848
　合計12060

これは下の計算と同一である。





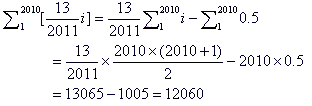
解答・その13

（ペンネ－ム：スモークマン）

地道だけど...高々...12までだから...計算しちゃいました...

0≦　　　　＜1...1≦x＜[2011/13=154.6]=154
1＜13x/2011＜2...155＜x＜[2*2011/13=309.3]=309...309-154=155
2＜　　　　＜3...310≦x＜[3*2011/13=464.0]=464...464-309=155
3＜　　　　＜4...465≦x＜[4*2011/13=618.7]=618...618-464=154
4＜　　　　＜5...619≦x＜[5*2011/13=773.4]=773...773-618=155
5＜　　　　＜6...774≦x＜[6*2011/13=928.1]=928...928-773=155
6＜　　　　＜7...929≦x＜[7*2011/13=1082.8]=1082...1082-928=154
7＜　　　　＜8...1083≦x＜[8*2011/13=1237.5]=1237...1237-1082=155
8＜　　　　＜9...1238≦x＜[9*2011/13=1392.2]=1392...1392-1237=155
9＜　　　　＜10...1393≦x＜[10*2011/13=1546.9]=1546...1546-1392=154
10＜　　　　＜11...1547≦x＜[11*2011/13=1701.6]=1701...1701-1546=155
11＜　　　　＜12...1702≦x＜[12*2011/13=1856.3]=1856...1856-1701=155
12＜　　　　＜13...1857≦x＜2011...2010-1856=154

合計=155(1+2+4+5+7+8+10+11)+154(3+6+9+12)
　　=155*12*4+154*15*2
　　=7440+4620
　　=12060

になるのか...^^;...計算が合ってれば...
巧い方法があるような数の並びですね...?
わたしにはわかりませんが...^^;...
6～7 を対称に、154-155-155-154-155-155-(154)-...になってますね♪
なぜなんだろぅ...?

閃きました!!
グラフで考えると…
横が0～2010、傾き 13/2011
これを、縦13、横2011 の長方形で考えてみる。
この内部の点の数/2 になるはず…13 と 2011 は互いに素だから、対角線上には格子点はないから!!
内部の点の数とは…
　　(13-1)(2011-1)=12*2010=24120
なので…この半分の24120/2=12060 個になるんですね ^^v♪
最初は...ピックの定理とか持ち出さなきゃいけないのかと思ったりして、この発想をスルーしてました...^^;
計算によるのと比べて何とシンプルかつ美しいことでしょう♪
自画自賛 ^^v

解答・その14

（ペンネ－ム：teki）

答え　　１２０６０

まともに計算するのはエクセルの助けが必要ですが、ガウスの足し算で簡単にでますね。
ガウス記号をはずした形でガウスの足し算（これもしゃれてますね。）を行うと、１３が１００５個できます。
ガウス記号がついているので、平均はこれより１少ない１２ですから、
１２×１００５＝１２０６０　ですね。

*　平均が１少ないというのは、２０１１が素数であることに基づくものです。
この条件がないと、単純に１引くことができなくなります。
つまり、途中に整数が発生しないので、ガウス記号をはずして計算しても結果に影響が出ないわけです。

解答・その15

（ペンネ－ム：Wasmath）

"13"は"23"の間違いかとも思ったのですが，ひとまず与えられた数値のもとで解いてみます。

[13×k/2011] を
　　　「y=(13/2011)x に x=k（整数)を代入して整数部分を求めたもの」
と解釈すれば，求める式の値は
　　　「長方形の内部 0＜x＜2011，0＜y＜13 で，対角線（を含んでそ）の下方にある格子点の個数」
を表す。
13と2011は互いに素であるから，対角線上には格子点は存在しないので，その個数は
　　　2010×12/2 = 12060　　（答）
ちなみに，13を23にしても「23と2011は互いに素」であることに変わりはないので，同様に
　　　2010×22/2 = 22110
となって，答の数値もちょっと面白い。

解答・その16

（ペンネ－ム：MVH）

まず, 拡張として, 次の問題を考察します.



互いに素な自然数 a,b に対して,
a=cb+d かつ 1≦d≦b-1
を満たす自然数の組(c,d)がただ一組存在します.
ここで, 自然数kに対して,

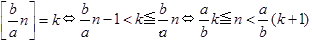・・・(1)

に注意します（k=0 の場合は, 求める和に影響しないため, 除外します）.
なお,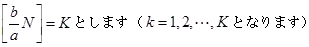

Ⅰ）k=be となる自然数 e が存在するとき（⇔k≡0 (mod　b) のとき）,
(1)⇔
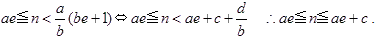
これより, (1)となる n の個数は,
　　(ae+c)-ae+1=c+1（個）.
なお,k=be となる自然数 e が存在するようなの k 個数は, 1からKまでの自然数に含まれる　bの倍数の個数に等しいですから、 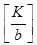で与えられます.

Ⅱ）k+1=bf となる自然数 f が存在するとき（⇔k+1≡0 (mod　b) ⇔k≡-1≡b-1 (mod　b) のとき）,
(1)⇔
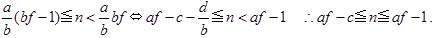
これより, (1)となる n の個数は,
　　(af-1)-(af-c)+1=c（個）.
なお,k+1=bf となる自然数 f が存在するようなの k 個数は,



Ⅲ）上記のⅠ）Ⅱ）以外ののとき（k≡1,2,・・・,b-2 (mod　b) のとき）,
(1)から,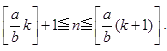
これより, (1)となる n の個数は,
(1)から,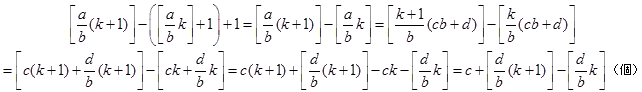
です.
さて, n=1,2,・・・ に対して, dn を b で割った余りは, 必ず周期を持ちます. さらに, その周期は, b 以下です（周期が b となるのは, d,b が互いに素のとき, です）.
また, 任意の自然数に対して, 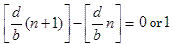です.
従って, n=1,2,・・・に対して, 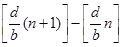は, 0 と 1 の数列を生みます.
そして, 和を求める際には, 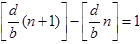となるにのみ着目すれば良いことが分かります.
以上で, 一般の場合の考察を終えます. □

以下では, 上記の考察を踏まえ, 問題169を解きます.
問題169は, 上記考察において,
　　a=2011,b=13,c=154,d=9,N=2010,K=12
の場合です.

Ⅰ）となるkは, 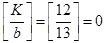個, つまり, Ⅰ）となることはありません.
また, N=pa=1 となる自然数 p が存在する（2010=1×2011-1）ので, Ⅱ）となる k は, 1 個あります（k=12）.
Ⅲ）において, (1)となる n の個数は, 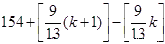（個） あります. 今, d=9 と b=13 は互いに素ですので, 9n（nは自然数）を 13 で割った余りは, 周期 13 です.
ここで, k=1,・・・,11,12 に対して, 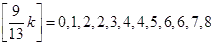に注意します（1 大きくなる n に着目します）.
以上により, 求める式の値を A とすると,


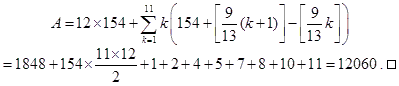
ところで, この問題を眺めていると, 次のことが気になりました.
2011は2011年度ということで良いとして, 13の意味は何だろう, と考えました. その 結果, この13は, 問題の出典である『2001年トライヤル問題』の2001年度＝平成13年 度から来ているのではないか, と推測しました. つまり, 問題の改題としては, 次の 問題が適当ではないか, ということで, 次の問題を考察してみます（2011年＝平成23 年）.


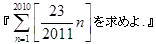
この問題は, 冒頭の拡張において,て,
　　a=2011,b=23,c=87,d=10,N=2010,K=22
の場合です.

Ⅰ）となるkは, 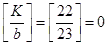個, つまり, Ⅰ）となることはありません.
また, N=pa=1 となる自然数 p が存在する（2010=1×2011-1）ので, Ⅱ）となる k は, 1 個あります（k=12）.
Ⅲ）において, (1)となる n の個数は, 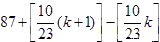（個） あります. 今, d=9 と b=13 は互いに素ですので, 9n（nは自然数）を 13 で割った余りは, 周期 13 です.
ここで, k=1,・・・,11,12 に対して, 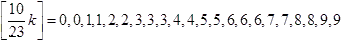に注意します（1 大きくなる n に着目します）.
以上により, 求める式の値を A とすると,




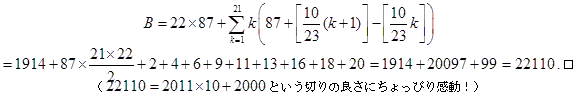
正解者

Wasmath teki 杖のおじさん
haya スモークマン 転位反応
のっこん falcon@中学教師 迷子の雄猫
浜田　明巳 T_Tatekawa エルドス
夜ふかしのつらいおじさん オヤジ ykak
MVH

コメント

13と2011は、互いに素（最大公約数が１の関係）ですから、

　　

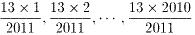
は、整数にはなりません。
この数列の前後を組み合わせると、その和はすべて13になります。

　　

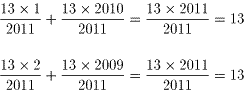
ガウス記号を考えると、小数点以下が切り捨てられることから、

　　

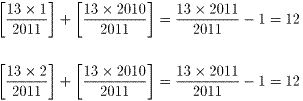
となります。この組合せが、1005個ありますから、
　　12×1005=12060
となります。Wasmathさん、MVHさんの ご指摘にあるように、23と2011の組合せで出題すれば良かったですね。

top