問題167 50枚のカード
1から50までの数字を1つずつ書いたカードが50枚あります。
このカードは、片面が青に、もう1つの面が赤にぬられていて、どちらの面も同じ数字が書かれています。
生徒が50人いるクラスの先生が50枚のカードをすべて青の面を上にして机に並べ、
「さあ、これから出席番号順に1番の人から1人ずつ前にでてきて、自分の出席番号の
倍数になるカードはすべて裏返し、青だったら赤に、赤だったら青にしてください。」と言いました。
さて、出席番号50番の最後の生徒が先生に言われたように裏返したあと、
赤の面が上になっているカードは何枚ありますか。
問題の出典
パズル気分で算数オリンピック
東大算数研究会
講談社
第5回算数オリンピック 予選問題
答えと解説
解答・その1
(ペンネ−ム:のっこん)
「約数が何個あるか」が問題になります
平方数の時だけ約数の個数が奇数になります
つまり、「平方数は何個あるか」が問われています
| 1のカードは1番が裏返す | 裏返し1回 | 赤が上 |
| 2のカードは1番・2番が裏返す | 裏返し2回 | 青が上 |
| 3のカードは1番・3番が裏返す | 裏返し2回 | 〃 |
| 4のカードは1番・2番・4番が裏返す | 裏返し3回 | 赤が上 |
| 5のカードは1番・5番が裏返す | 裏返し2回 | 青が上 |
| 6のカードは1番・2番・3番・6番が裏返す | 裏返し4回 | 〃 |
| 7のカードは1番・7番が裏返す | 裏返し2回 | 〃 |
| 8のカードは1番・2番・4番・8番が裏返す | 裏返し4回 | 〃 |
| 9のカードは1番・3番・9番が裏返す | 裏返し3回 | 赤が上 |
| 10のカードは1番・2番・5番・10番が裏返す | 裏返し4回 | 青が上 |
| ・・・・・・・・・・・・・・・・・・ | ||
| 49のカードは1番・7番・49番が裏返す | 裏返し3回 | 赤が上 |
| 50のカードは1番・2番・5番・10番・25番・50番が裏返す | 裏返し6回 | 青が上 |
赤が上になるのは平方数の時です
1から50までの中に平方数は
12、22、32、42、 52、62、72
の7個あるから
答は7枚です
解答・その2
(ペンネ−ム:スモークマン)
赤になってるってことは奇数回裏返ってること...
逆に青のカードは偶数回裏返ってること...
各数字の倍数を裏返すということは...
その数字に関しては...
約数が偶数個あるとき青になってることと同じなので...
約数が偶数個=約数の大きさの順に並べると...
二乗数になることと同じ♪
つまり...50>72〜12...7個
ですね ^^
解答・その3
(ペンネ−ム:オヤジ)
裏返される回数が、奇数回となれば良いから,問題134の,記号<A>を用いて
<A>:自然数Aの約数の個数 とすると
<1>=1 <26>=<2・13>=4 <2>=2 <27>=<33>=4 <3>=2 <28>=<22・7>=6 <4>=<22>=3 <29>=2 <5>=2 <30>=<2・3・5>=8 <6>=<2・3>=4 <31>=2 <7>=2 <32>=<25>=6 <8>=<23>=4 <33>=<3・11>=4 <9>=<32>=3 <34>=<2・17>=4 <10>=<2・5>=4 <35>=<5・7>=4 <11>=2 <36>=<22・33>=9 <12>=<22・3>=6 <37>=2 <13>=2 <38>=<2・19>=4 <14>=<2・7>=4 <39>=<3・13>=4 <15>=<3・5>=4 <40>=<23・5>=8 <16>=<24>=5 <41>=2 <17>=2 <42>=<2・3・7>=8 <18>=<2・32>=6 <43>=2 <19>=2 <44>=<22・11>=6 <20>=<22・5>=6 <45>=<32・5>=6 <21>=<3・7>=4 <46>=<2・23>=4 <22>=<2・11>=4 <47>=2 <23>=2 <48>=<24・3>=10 <24>=<23・3>=8 <49>=<72>=3 <25>=<52>=3 <50>=<2・52>=6上記計算より「赤」となるのは、1〜50の平方数
∴ カード{1,4,9,16,25,36,49}の 7枚
解答・その4
(ペンネ−ム:迷子の雄猫)
ある数の自乗ではない整数nは、1とn、2とn/2というように、
約数を偶数個持つ。よって、最終的に奇数回 裏にされて、
赤の面が上になっているのは、整数の自乗になっている整数、
1、4、9、16、25、36、49の7枚。
解答・その5
(ペンネ−ム:ykak)
答え 7枚
考え方
カードは、偶数回裏返しにされると元に戻って青のままになるので、問題は奇数回裏返しされ
るカードの枚数を見つければよいということになる。
生徒の出席番号の倍数に当たるカードを裏返すということは、カードのほうから言
えば、出席番号がそのカードに書かれている数字の約数になっているとき、裏返さ
れるということになる。
1とそのカード自身の数字も約数に含むとすると、出席番号1の生徒はすべての
カードを裏返し、またどのカードもその数字に等しい出席番号を持つ生徒はそのカ
ードを裏返すので、この関係ではすべてのカードは合計2回裏返されるから、カード
の色は変わらない。
そうすると問題は、1とそのカードの数字の間にある約数の個数によって決まるこ
とが分かる。
ある出席番号がそのカードの約数になる場合、その出席番号をその約数で割った
時の商もそのカードの数字の約数であるから、約数は常に2つずつ1組あることに
なり、1とそのカードの数字の間にある約数の個数全体は偶数個ある。そしてこれ
らの約数を出席番号に持つ生徒が、1回ずつカードを裏返すから、個々のカードは
偶数回裏返されることになり、カードの色は変わらないということになる。
ただしカードの数字が平方数である場合はこの例外となり、その平方根に関して
は上のような約数の組がないので、この場合約数は1個しかない。平方数でも、平
方根以外の約数があれば、それについては上の意味での約数の組があるので、
結局平方数については、約数が奇数個になるということが言える。
従ってカードの数字が平方数である場合だけ裏返す回数は奇数となり(ただし1
は出席番号1の生徒が1回裏返すだけであることは明らか)、この
カードだけが最後に赤になっているということになる。
1から50までの間の平方数は、1、4、9、16、25、36、49のみで
あるから答えは7枚になる。
解答・その6
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
答え 赤のカードは7枚です。
1から50までの整数のそれぞれの約数の数を求めます。
その数が奇数である数は赤色になります。
約数の数が奇数になる数は次の1,4,9,16,25,36,49 の7個です。
1は 1 1個
4は 1,2,4 3個
9は 1.3.9 3個
16は 1,2,4,8,16 5個
25は 1,5,25 3個
36は 1,2,3,4,6,9、12,18,36 9個
49は 1,7,49 3個
従って赤のカードは7枚となります。
解答・その7
(ペンネ−ム:転位反応)
カードを裏返す回数は、そのカードに書かれている数の約数の個数によって決まる。
約数の個数は平方数は奇数、平方数以外は偶数なので、奇数の場合のカードは赤色、
偶数の場合のカードは青色になる。
例えば、1〜10の数について整理すると下表の通り。
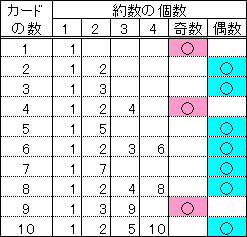
さて、1〜50の数のうち、平方数は、1、4、9、16、25、36、49 の7個なので、
約数の個数、カードの色について整理すると以下の通り。
よって、赤が上になっているカードの数は7枚である。

解答・その8
(ペンネ−ム:T_Tatekawa)
カードに書かれている数字の約数を考えます.
約数の個数が偶数のものは青の面が上になります.
例えば 12 は 1, 2, 3, 4, 6, 12 なので,
合わせて6回ひっくり返されて青の面が最後に上になります.
約数の個数が奇数になるのは平方数です.
1, 4, 9, 16, 25, 36, 49 は全て,自然数の2乗です.
1: 1
4: 1, 2, 4
9: 1, 3, 9
16: 1, 2, 4, 8, 16
25: 1, 5, 25
36, 1, 2, 3, 4, 6, 9, 12, 18, 36
49: 1, 7, 49
これらは最終的に赤の面が上になります.
よって,答えは 7 個です.
解答・その9
(ペンネ−ム:MVH)
〔解答〕
nという数字が書かれた一枚のカードに着目します。
このカードが裏返されるのは、出席番号が「nの正の約数」番の生徒によって、です。
それ以外にはありません。
始めにカードは全て青の面を上にしてあるので、50番目の生徒が作業を終えたとき、
このカードが赤の面を上にするためには、「nの正の約数」が奇数個あることが必要かつ十分です。
従って、以上のことから、求めるカードの枚数は、
「1から50までの自然数のうちで、正の約数を奇数個もつ自然数の個数」
と同じことが分かります。
まず、1はこれに含まれます。
以下では、nを2以上の自然数とします。2以上の任意の自然数nは、
n=p1s1・p2s2・・・pNsN
(但し、piは素数で、p1<p2<・・・<pNとする。
また、siは正整数とする。)
と表せます。このとき、nの正の約数の個数は、
(s1+1)(s2+1)・・・(sN+1)
と書けます(これは既知とします)。
これが、奇数であるためには、任意の i に対して、si+1が奇数、
すなわち、siが偶数であることが必要かつ十分です。
従って、結局、求めるカードの枚数は、
「(2から50までの自然数のうちで、素因数分解したときに、各素数が偶数個ある自然数の個数)+1」si
と同じことになります。
これを求めるためには、1から50までの自然数を全て素因数分解する必要は無く、次のように求まります。
22=4、24=16、32=9、52=25、
72=49
に注意すると、条件を満たす自然数は、これら以外には、
22×32=36
しかないことが分かります。1が条件を満たすことに注意すると、
求めるカードの枚数は、7枚です。(答え)
解答・その10
(ペンネ−ム:やなせ)
最初は青なので最終で赤になっているのは奇数回数返された札だけになる。
出席番号の倍数時のみ該当する札を裏返すとの条件なので各札番号の約数の数を調べれば解る
約数の数が奇数になるのは札番号が二乗で求められる札になるから
√50=7.07106
答え 7枚
解答・その11
(ペンネ−ム:falcon@中学教師)
<答え> 7枚
<考え方>
カード1枚1枚に注目して考える。
あるカードはそのカードの数字の「約数」の出席番号の人が裏返すことになる。
するとカードは次のような2種類に分けて考えることができる。
カードの数が平方数 → 約数が奇数個 → 奇数回ひっくり返す → 最終的に赤
カードの数がそれ以外 → 約数が偶数個 → 偶数回ひっくり返す → 最終的に青
つまり平方数が何枚あるかがこの問題の答えに結びつく。
50までの平方数は1,4,9,16,25,36,49の7枚なので赤の面が上になっているカードは7枚。
解答・その12
(ペンネ−ム:長崎島原 かがみ)
約数の個数が奇数のとき赤,偶数のとき青となる。
1〜50の整数の中で,約数の個数が奇数であるのは
1,4,9,16,25,36,49
の7個だけである。
したがって,最後に赤になっているのは7枚である。
答 7枚
解答・その13
(ペンネ−ム:haya)
赤の面が上になっているカードは 7 枚です。
【解き方】
色が青から赤に変わるカードは 1 とその数自身を含む約数を奇数個持つ種類のカードです。
1〜50 までの整数でこのような整数が何個あるかという問題と同じですから、7 が答えです。
7 個の整数の内訳は、
| No. | 整数 | 約数の個数 | 約数の内訳 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 4 | 3 | 1, 2, 4 |
| 3 | 9 | 3 | 1, 3, 9 |
| 4 | 16 | 5 | 1, 2, 4, 8, 16 |
| 5 | 25 | 3 | 1, 5, 25 |
| 6 | 36 | 9 | 1, 2, 3, 4, 6, 9, 12, 18, 36 |
| 7 | 49 | 3 | 1, 7, 49 |
です。
解答・その14
(ペンネ−ム:teki)
<答え> 7枚
50枚程度なら、実際にやってみてもできそうですが、それでは面白くないので
算数的な解答を。
<解法>
1〜50までの平方数の個数を数えました。(これが一番早い解法でしょうね)
理由は約数(1とその数を含む)の個数が奇数になるのは、平方数のみだからです。
約数の個数が奇数だと、カードは赤に、偶数だと青になります。(裏返される回数が奇数だと赤、偶数だと青ですね。)
一般的に約数の個数が奇数となるのは、平方数のみです。
解答・その15
(ペンネ−ム:シュレーディンガーの三毛猫)
【答】7枚
【解法】
生徒が自分の出席番号の倍数になるカードをすべて裏返すので、
各カードは書かれた数字の約数の個数回裏返されることになる。
初めは全て青の面が上なので、最終的に上の面が赤になるのは、
約数の個数が奇数となる数の書かれたカードである。
ある数を素因数分解したときの各素数の指数を、
小さい素数から順にa1,a2,a3・・・とおくとき、
その数の約数の個数は
(1+a1)(1+a2)(1+a3)・・・
と表せる。
そのうち、約数の個数が奇数となるのは
素数の指数a1,a2,a3・・・がすべて偶数となるとき、
すなわち平方数のときに限られる。
1から50までの自然数のうち、平方数は
1,4,9,16,25,36,49の7個なので、
上の面が赤となる枚数は7枚となる。
解答・その16
(ペンネ−ム:夜ふかしのつらいおじさん)
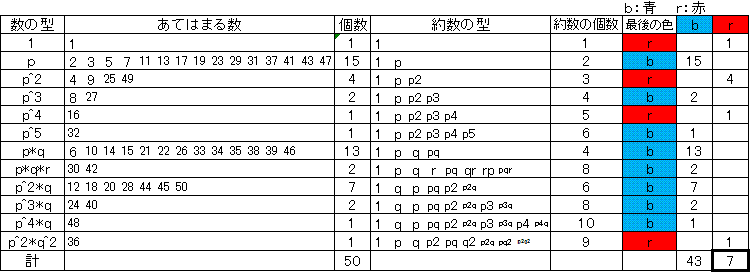
1から50までの数を分類します。(カードの数)
それぞれの素因数を、p,q,rとします。
それぞれの型の約数の個数を数えます。(裏返す生徒の人数)
例えば、「10」のカードは、約数が{1,2,5,10}なので、4人の生徒が裏返します。
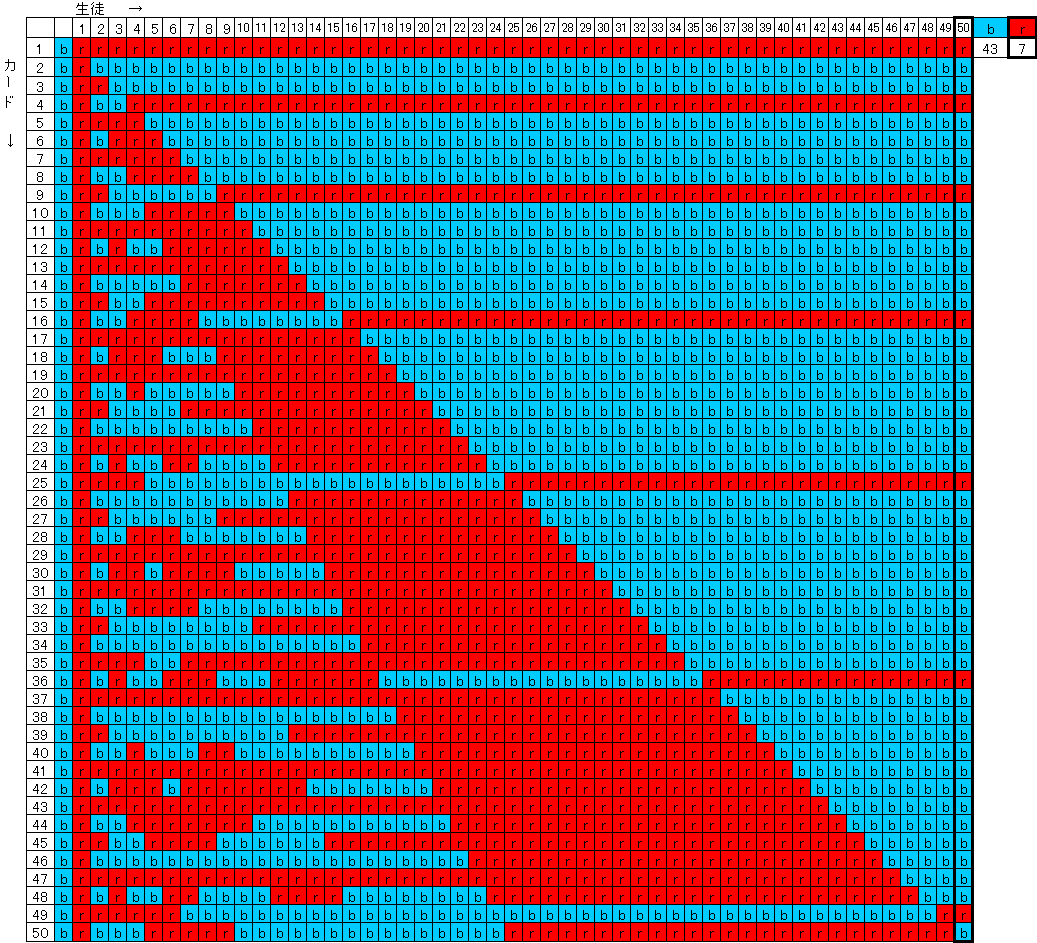
青から始まって、裏返しの回数が奇数なら赤、偶数なら青です。
はじめ青の「10」のカードは、1番の生徒により赤、2番の生徒により青、5番の生徒により赤、10番の生徒により青になります。
このように数えていくと50番の生徒が裏返したあと赤のカードは、7枚です。
つまり、1を含んで約数の個数が奇数個のカードの枚数になります。
解答・その17
(ペンネ−ム:三角定規)
【解答】<三角定規>
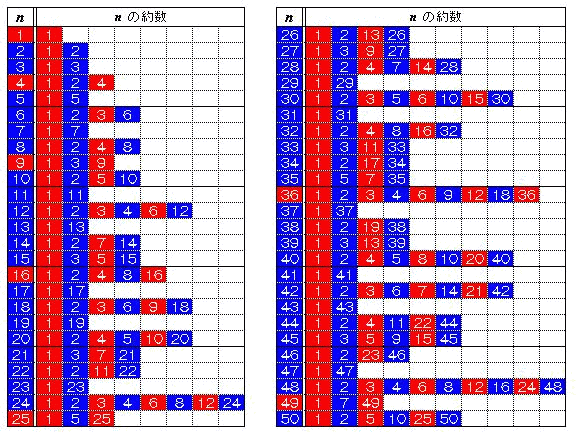
例えば数20は,1,2,4,5,10,20 の 6 個の約数をもつから,
1,2,4,5,10,20番の生徒が通過するたびに赤・青・赤・青・赤・青 と 6 回(偶数回)反転し,青 となる。
よって,数 N の約数が偶数個ならばカード N は 青,奇数個ならば 赤 となる。
N が非平方数のとき,a が N の約数ならば N/a も N の約数だから,N の約数は偶数個。
N が平方数 (=m2) のとき,√N=m 以外の約数は偶数個で,それに m を加えて約数は奇数個。
よって,N が非平方数ならばカード N は青,平方数ならば 赤 となり,赤 の枚数は
1,4,9,16,25,36,49 の 7枚。
解答・その18
(ペンネ−ム:エルドス)
解答 赤は7枚
面白い約数の問題かと思ってプログラムを組みましたが、出た答えを見て、奇数回ひっくり返るのは2乗のときだけだと気付きました。
CLEAR
DIM a(50)
FOR i=1 TO 50
FOR j=1 TO i
IF MOD(i/j,1)=0 THEN LET a(i)=a(i)+1
NEXT j
NEXT i
FOR i=1 TO 50
PRINT i,a(i)
IF MOD(a(i),2)=1 THEN LET c=c+1
NEXT i
PRINT "c=";c
END
解答・その19
(ペンネ−ム:浜田 明巳)
赤の数を数えるので,青を0,赤を1で表す.50枚のカードの色をa(j)(1≦j≦50)として,50人分の倍数のカードの色を変える.
次のエクセルのマクロを組み,答を7と求めた.
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Dim a(50) As Integer
Dim j As Integer
Dim jj As Integer
Dim jjj As Integer
For j = 1 To 50
a(j) = 0
Cells(j, 1).Value = 0
Next j
For j = 1 To 50
jj = 1
While j * jj <= 50
jjj = j * jj
a(jjj) = 1 - a(jjj)
jj = jj + 1
Wend
For jj = 1 To 50
Cells(jj, j + 1).Value = a(jj)
Next jj
Next j
Cells(51, 1).Value = "=SUM(AY1:AY50)"
Range("A51").Select
End Sub
解答・その20
(ペンネ−ム:再出発)
算数で解いたのではなくエクセルのマクロを組んでみたので、参考程度に送ります。
エクセルで動かしてみると、おもしろいかも知れません。
標準モジュールにコピーし、空いているシートをアクティブにして実行してください。
50人の子供たちがカードを裏返していく様が見えるようです。
Sub MATH167()
Dim LD As Range
Set LD = Range("C3")
Range("B2:L7").Select
With Selection.Borders(xlInsideVertical)
.LineStyle = xlContinuous
End With
With Selection.Borders(xlInsideHorizontal)
.LineStyle = xlContinuous
End With
For J = 1 To 10: LD(0, J) = J: Next
Range(LD(0, 1), LD(0, 10)).Select
Selection.Interior.ColorIndex = 19
For J = 1 To 5: LD(J, 0) = J * 10 - 10: Next
Range(LD(1, 0), LD(5, 0)).Select
Selection.Interior.ColorIndex = 20
' ここまでは枠を描いています
For J = 1 To 5
For K = 1 To 10
Range(LD(J, K), LD(J, K)).Select
Selection.Interior.ColorIndex = 24
LD(J, K) = 24
Next
Next
' ここまで、青い面で並べました。
' これから子供たちがカードを裏返していきます。
For J = 1 To 50: LD(-1, 1) = J
For K = 1 To 50: LD(-1, 2) = K
For L = 1 To 2000: For M = 1 To 2000: Next: Next ' 色塗り時間
'調節
NO = J * K
If NO > 50 Then GoTo EX
LY = (NO - 1) \ 10 + 1: LX = (NO - 1) Mod 10 + 1
LD(LY, LX) = 23 + 23 - LD(LY, LX)
Range(LD(LY, LX), LD(LY, LX)).Select
Selection.Interior.ColorIndex = LD(LY, LX)
Next
EX:
Next
End Sub

正解者
| teki | haya | のっこん |
| falcon@中学教師 | 夜ふかしのつらいおじさん | スモークマン |
| 杖のおじさん | ykak | 転位反応 |
| 浜田 明巳 | オヤジ | エルドス |
| シュレーディンガーの三毛猫 | 迷子の雄猫 | やなせ |
| 再出発 | 長崎島原 かがみ | 三角定規 |
| MVH | T_Tatekawa |
コメント
約数の個数の偶奇の問題ですね。約数の個数が奇数になる場合というのは、その数が平方数で
あるということがわかると、その数を求めるのは簡単ですね。
約数の個数の求め方については、MVHさん、シュレーディンガーの三毛猫さんが示してくださいました。
 top
top