栤戣166丂偟傑偟傑偺挿曽宍
摨偠戝偒偝偺崟丄敀俀庬椶偺惓曽宍偺巻偑丄摨偠枃悢偢偮偁傝傑偡丅
俙偝傫偑丄傑偢敀偺巻傪偡偒傑側偔側傜傋偰挿曽宍傪偮偔傝傑偡丅
師偵丄俛偝傫偑偦偺傑傢傝傪崟偺巻偱偡偒傑側偔埻傒傑偡丅
偝傜偵丄偦偺傑傢傝傪丄俙偝傫偑敀偺巻偱偡偒傑側偔埻傒傑偡丅
偙傟傪孞傝曉偟偰偄偭偰丄俛偝傫偑俆夞丄崟偺巻偱埻傒廔偊偨偲偒偵丄
崟偺巻傕敀偺巻傕侾枃傕梋傞偙偲側偔巊偄愗傝傑偟偨丅
崟偲敀偺巻偺崌寁偼丄嵟傕彮側偄応崌偵壗枃偱偟傚偆偐丅
栤戣偺弌揟
僷僘儖婥暘偱嶼悢僆儕儞僺僢僋
搶戝嶼悢尋媶夛
島択幮
戞俁夞嶼悢僆儕儞僺僢僋丂寛彑栤戣
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
妏偺晹暘偩偗傪峫偊偰傒傞偲...
A*B...W... 偱巒傑偭偨傜...
師偼...2(A+B)+4*12...B
偦偺師偼...2(A+B)+4*(22-12)...W
偦偺師偼...2(A+B)+4*(32-22)...B
...
嵟屻偼...2(A+B)+4*(92-82)...B
偩偐傜...
W=A*B+4*2(A+B)+4*(22+42+62+82-12-32-52-72)
B=5*2(A+B)+4*(12+32+52+72+92-22-42-62-82)
W+B=A*B+18(A+B)+4*92
B-W=0=2(A+B)-A*B+8(12+32+52+72-22-42-62-82)+4*92
偐傜...
2(A+B)-A*B+36=0
A(B-2)-(B-2)=36+4=40
(A-2)(B-2)=40
A-2=5, B-2=8
A=7, B=10...A,B 偼擖傟懼傢偭偰傕偄偄...
W+B=A*B+18(A+B)+4*92
=7*10+18(7+10)+4*92
=70+306+324
=700 枃
偱偄偄偺偐側...^^;?
夝摎丒偦偺2
乮儁儞僱亅儉丗柪巕偺梇擫乯
偆乣傓丠偙傟乮*1乯傪庤寁嶼偱夝偗傞偺偱偟傚偆偐丠
偄偊丄帪娫傪妡偗傟偽夝偗傑偡偗傟偳傕丅
嵟弶偵俙偝傫偑丄敀偺巻傪偡偒傑側偔暲傋偰嶌偭偨挿曽宍偺戝偒偝傪丄倣仏値偲偍偔丅
崟偺巻偱廃傝傪埻傓偲丄巊梡偟偨崟偺巻偼俀倣亄俀値亄係枃丅
偝傜偵敀偺巻丄崟偺巻偺弴偱廃傝傪埻傓偲丄
堦搙埻傓偛偲偵曈偺挿偝偑俀枃偯偮戝偒偔側傞偺偱丄
崟偺巻偺傎偆偑俉枃懡偔側傞丅傛偭偰丄
丂丂俀倣亄俀値亄係亄乮俉仏係乯亖倣仏値
偮傑傝
丂丂俀倣亄俀値亄俁俇亖倣仏値丂丂丂丂丂.....乮*1乯
偲偄偆曽掱幃偑惉傝棫偮丅惀傪夝偄偰丄
乮俇丆侾俀乯乮俈丆侾侽乯乮俁丆係俀乯乮係丆俀俀乯亅弴晄摨亅
巻偺枃悢偑嵟傕彮側偔側傞偺偼乮倣丆値乯偑乮俈丆侾侽乯亅弴晄摨亅偺応崌偱丄
巻偺憤枃悢偼丄廲墶傪侾俉枃偯偮憹傗偟偨俀俆仏俀俉亖俈侽侽枃
夝摎丒偦偺3
乮儁儞僱亅儉丗ykak乯
摎偊丂丂俈侽侽枃
峫偊曽
弶傔偺挿曽宍偺廲墶偺枃悢傪偦傟偧傟倃丆倄偲偡傞丅
弶傔偺挿曽宍偵巊偭偨敀偺巻偺枃悢偼倃倄丅
侾夞栚偵偙傟傪庢傝姫偄偰抲偄偨崟偺巻偺悢偼
丂丂丂崟乮侾夞栚乯丂 2(X + Y乯 + 4
師偵敀偑抲偔巻偺枃悢偼
丂丂丂敀丂丂丂丂丂丂2(X + Y 乯+ 12
埲壓丄弴師
丂丂丂崟乮俀夞栚乯丂2(X + Y乯 + 20
丂丂丂敀丂丂丂丂丂丂2(X + Y乯 + 28
丂丂丂崟乮俁夞栚乯丂2(X + Y乯 + 36
丂丂丂敀丂丂丂丂丂丂2(X + Y乯 + 44
丂丂丂崟乮係夞栚乯丂2(X + Y乯 + 52
丂丂丂敀丂丂丂丂丂丂2(X + Y乯 + 60
丂丂丂崟乮俆夞栚乯丂2(X + Y乯 + 68
敀偲崟偦傟偧傟偺枃悢傪懌偡偲丄敀偼
丂丂丂XY丂+丂8乮X 亄 Y乯 亄 144丂亅亅亅(1)
崟偼
丂丂丂10乮X + Y乯 亄 180丂亅亅亅(2)
偙傟偑摍偟偄偙偲偐傜摍崋偱偮側偄偱惍棟偡傞偲
丂丂丂XY 亖 2乮X + Y乯 + 36丂亅亅亅(3)
偙偺幃傪枮偨偡X偲Y偺惍悢抣傪尒偮偗傟偽傛偄偑丄偙偺愭偑暘偐傜側偄偺偱丄C偺僾儘僌儔儉偱丄X丄
Y偦傟偧傟侾侽侽傑偱傪扵嶕偟偰傒傞偲丄乮俁丆係俀乯丄乮係丆俀俀乯丄乮俇丆侾俀乯丄乮俈丆侾侽乯
偺係偮偺慻偑尒偮偐傝傑偟偨丅
偙偺拞偱枃悢傪嵟彫偵偡傞偺偼乮俈丆侾侽乯偺慻傒側偺偱丄偙傟偑惓夝偲偄偆偙偲偵側傝偦偆偱偡丅
偙傟傪(1)偲(2)偵摉偰偼傔傞偲丄偦傟偧傟俁俆侽偲側傝丄摎偊偼偙傟傪崌寁偟偨俈侽侽枃偵側傝傑偡丅
屻偐傜峫偊偰傒傞偲丄壖偵X丄Y偳偪傜傕侾侽侽偲偟偰傒傞偲丄XY偑侾侽侽侽侽偲側傞偑丄(3)偺塃曈偼偦傟傛傝
傕彫偝偄悢偵側傞偐傜丄X丄Y嫟偵侾侽侽偲偄偆偙偲偼偁傝摼側偄偟丄X偲Y偑偦傟傛傝傕戝偒偔側傞偲(3)偺嵍曈
偼傑偡傑偡戝偒偔側傝丄塃曈偲摍偟偔側傞偙偲偼偁傝摼側偄偐傜丄X偲Y偲傕侾侽侽傛傝戝偒偄斖埻偼挷傋側偔偰
傕椙偝偦偆偲偄偆偐丄(3)偺摎偊偼忋偺係慻偟偐側偝偦偆偱偡偹丅
僷僜僐儞傪巊傢側偄応崌偼丄偙偺曈傝偐傜摎偊傪尒偮偗偰峴偔偺偱偟傚偆偐丅崱夞偼僷僜僐儞偵棅傝傑偟
偨偑堦墳搳峞偟傑偡丅
夝摎丒偦偺4
乮儁儞僱亅儉丗falcon@拞妛嫵巘乯
亙摎偊亜700枃
亙峫偊曽亜
1夞栚偺敀偺挿曽宍傪恾偺傛偆偵俀偮偺晹暘偵偟偰峫偊傞丅
嵟傕奜懁偺1楍偵埵抲偡傞晹暘乮恾偺敀偄晹暘乯偑倶屄
偦偺倶屄偵埻傑傟偨晹暘乮恾偺幬慄晹暘乯偑倷屄丂偲偡傞丅
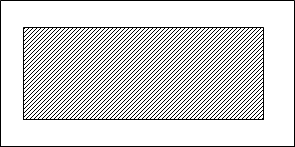
嶌嬈偺搙偵怴偨偵巊梡偟偨巻偼埲壓偺捠傝丅
丂敀侾夞栚丂丂倶亄倷屄丂丂崟侾夞栚丂丂倶亄俉屄
丂敀俀夞栚丂丂倶亄16屄丂丂崟俀夞栚丂丂倶亄24屄
丂敀俁夞栚丂丂倶亄32屄丂丂崟俁夞栚丂丂倶亄40屄
丂敀係夞栚丂丂倶亄48屄丂丂崟係夞栚丂丂倶亄56屄
丂敀俆夞栚丂丂倶亄64屄丂丂崟俆夞栚丂丂倶亄72屄
敀偺憤悢偼丂5倶亄倷亄160屄丄崟偺憤悢偼丂5倶亄200屄丅
敀偲崟偺憤悢偼摍偟偄偺偱丄倷亖40
倷偺僷僞乕儞偼埲壓偺捠傝丅
(1)侾亊40丂(2)俀亊20丂(3)係亊10丂(4)俆亊俉
偦傟偧傟偵偮偒丄倶偺抣偼
(1)倶亖46丂(2)倶亖48丂(3)倶亖32丂(4)倶亖30
偲側傞偺偱丄嵟傕彮側偔側傞偺偼(4)偺偲偒偲傢偐傞丅
偟偨偑偭偰媮傔傞枃悢偼
(5倶亄倷亄160)亄(5倶亄200)亖(5亊30亄40亄160)亄(5亊30亄200)亖350亄350亖700
夝摎丒偦偺5
乮儁儞僱亅儉丗僆儎僕乯
乮嘥乯侾夞栚
丂敀丂丂丂mn丂枃丂丂佹丂椺偊偽丂廲 n 枃丆墶 m 枃丂扐偟 m亞n 偲偟偰堦斒惈偼幐傢傟側偄丂
丂崟丂丂丂2(m+n)+4丂枃
乮嘦乯俀夞栚
丂敀丂丂丂2{(m+2)+(n+2)}+4丂枃
丂崟丂丂丂2{(m+4)+(n+4)}+4丂枃
乮嘨乯俁夞栚
丂敀丂丂丂2{(m+6)+(n+6)}+4丂枃
丂崟丂丂丂2{(m+8)+(n+8)}+4丂枃
乮嘩乯係夞栚
丂敀丂丂丂2{(m+10)+(n+10)}+4丂枃
丂崟丂丂丂2{(m+12)+(n+12)}+4丂枃
乮嘪乯俆夞栚
丂敀丂丂丂2{(m+14)+(n+14)}+4丂枃
丂崟丂丂丂2{(m+16)+(n+16)}+4丂枃
乮嘥乯乣乮嘪乯偐傜
敀偺枃悢亖崟偺枃悢傛傝丂mn + 8m + 8n + 144 = 10m + 10n + 180丂丒丒丒丒乮A乯
廬偭偰丂(m-2) (n-2)=40
忋幃偑乮A乯偺椉曈偑嵟彫偲側傞偺偼丆m=10 , n=7丂偺偲偒偺丂俁俆侽枃
丂丂丂亪丂俈侽侽枃
夝摎丒偦偺6
乮儁儞僱亅儉丗偄偲偆傂傠備偒乯
俀夞偔傜偄墢庢偭偰傒偰丄朄懃傪妋擣偟偰偐傜晛捠偵曽掱幃傪嶌偭偰夝偒傑偟偨丅
嵟弶偺敀挿曽宍偺廲傪a丄墶傪b偲偡傞偲乮a亞b偲偡傞乯
堦夞栚偺崟墢庢傝偼(a+1)*2+(b+1)*2丂枃昁梫偱
師偺敀墢庢傝偼(a+3)*2+(b+3)*2丂枃昁梫
擇夞栚偺崟墢庢傝偼(a+5)*2+(b+5)*2丂枃昁梫
丒丒丒
屲夞栚偺崟墢庢傝偼(a+17)*2+(b+17)*2丂枃昁梫
偙偙傑偱偵昁梫側枃悢偼
丂丂敀丂a*b+8(a+b)+144 枃丂丒丒丒丂(1)
丂丂崟丂10(a+b)+180 枃丂丂丂丒丒丒丂(2)
(1) = (2)傪夝偔偲
丂丂a*b-2(a+b)-36=0
曄宍偝偣偰
丂丂(a-2)(b-2)=40丂丂丒丒丒丂(3)
(3)幃偲a,b偑帺慠悢偱偁傞偙偲偐傜
丂丂(a-2,b-2)=(8,5),(10,4),(20,2),(40,1)
忋婰傛傝敀偲崟偺枃悢偑堦抳偡傞偺偼
丂丂(a,b)=(10,7),(12,6),(22,4),(42,3) 偺4捠傝偺傒
偦偺帪偺崌寁枃悢偼
丂丂(1) + (2)傛傝丂a*b+18(a+b)+324 枃丂丒丒丒丂(4)
(4)幃偼丂(a+18)*(b+18) 偲曄宍偱偒丄
嵟傕彮側偔側傞偺偼a+b偑嵟彫偵側傞(a,b)=(10,7)丂偺偲偒偱
摎偊丏700枃丂丂乮廔乯
傆偲婥偯偄偨偺偱偡偑丄
敀亖崟偲側傞偲偒偼崌寁偑丂a*b*10丂枃偵側傝傑偡丅
嬼慠側偺偐懠偵傕偁傞偺偐傪峫嶡偡傞偲
(4)亖a*b*10 偲偍偄偰丄曄宍偡傞偲
丂丂9ab-18(a+b)-324=0
丂丂ab-2(a+b)-36=0
丂丂(a-2)(b-2)=40丂偲丄(3)幃偲堦抳偡傞偺偱
敀偲崟偺崌寁偑a*b*10偱昞偝傟傞偲偒偵丄
忢偵敀偲崟偺枃悢偑堦抳偡傞
側傫偩偐晄巚媍偱偡丅
夝摎丒偦偺7
乮儁儞僱亅儉丗teki乯
亙摎偊亜丂丂俈侽侽枃
亙夝朄亜
晄掕曽掱幃偱偡偑丄偦偙傑偱偺摴偺傝偑挿偐偭偨丒丒丒丒丅
嵟弶偵倣亊値枃偱挿曽宍傪嶌偭偨偲偡傞偲丄師偺崟偑俀倣亄俀値亄係枃丄
偦偺師偺敀偑俀倣亄俀値亄侾俀枃丒丒丒丄埲壓摨條偱枃悢偼俉枃偢偮憹偊偰偄偒傑偡丅
偱丄寢嬊丄敀偼倣亊値亄俉倣亄俉値亄侾係係枃丄崟偼侾侽倣亄侾侽値亄侾俉侽枃丂暲傋傞
偙偲偵側傝傑偡丅
偙傟偑摍偟偄偺偱丄倣亊値亅俀倣亅俀値亅俁俇亖侽
偙偺晄掕曽掱幃偺惍悢夝偼丄乮俈丆侾侽乯丄乮俇丆侾俀乯丒丒丒丒丒偱偡偑丄崌寁枃悢偑嵟彫
偵側傞偺偼丄乮倣丄値乯亖乮俈丆侾侽乯偺応崌偱丄敀崟偲傕俁俆侽枃暲傋偨偙偲偵側傝傑偡丅
夝摎丒偦偺8
乮儁儞僱亅儉丗嶰妏掕婯乯
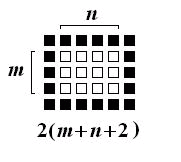 嵟弶 A 偝傫偑仩偱 m亊n (m亝n) 偺挿曽宍傪嶌偭偨偲偡傞偲丆
偦傟傪埻傓偺偼 2(m亄n亄2) 枃偺仭偩偐傜丆仩仭偺枃悢偼弴師埲壓偺傛偆偵側傞丅
嵟弶 A 偝傫偑仩偱 m亊n (m亝n) 偺挿曽宍傪嶌偭偨偲偡傞偲丆
偦傟傪埻傓偺偼 2(m亄n亄2) 枃偺仭偩偐傜丆仩仭偺枃悢偼弴師埲壓偺傛偆偵側傞丅
| 丂 | 仩 | 仭 |
|---|---|---|
| 侾夞栚 | mn | 2(m亄n亄2) |
| 俀夞栚 | 2((m亄2)亄(n亄2)亄2) | 2((m亄4)亄(n亄4)亄2) |
| 俁夞栚 | 2((m亄6)亄(n亄6)亄2) | 2((m亄8)亄(n亄8)亄2) |
| 係夞栚 | 2((m亄10)亄(n亄10)亄2) | 2((m亄12)亄(n亄12)亄2) |
| 俆夞栚 | 2((m亄14)亄(n亄14)亄2) | 2((m亄16)亄(n亄16)亄2) |
| 寁 | mn亄8(m亄n)亄144 | 10(m亄n)亄180 |
仩仭偺枃悢偑摍偟偄偙偲偐傜丂丂mn亄8(m亄n)亄144亖10(m亄n)亄180
丂亪 mn亅2(m亄n)亄4亖(m亅2)(n亅2)亖40
丂亪 (m亅2丆n亅2)亖(1丆40)丆(2丆20)丆(4丆10)丆(5丆8)
丂亪 (m丆n)亖(3丆42)丆(4丆22)丆(6丆12)丆(7丆10)
偦傟偧傟偺偲偒丆崌寁枃悢偼弴偵 1260丆880丆720丆700 偲側傞偐傜丆嵟傕彮側偄偺偼
丂丂 (m丆n)亖(7丆10) 偺偲偒偺 寁 700 枃乧乵摎乶
夝摎丒偦偺9
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
師偺恾偼丄A丄B偑岎屳偵敀丄崟偺巻偱埻偭偰偄偭偨偲偒偺嵍忋偺晹暘傪帵偟傑偡丅
懠偺俁僇強偺妏傕條巕偼摨偠偱偡丅
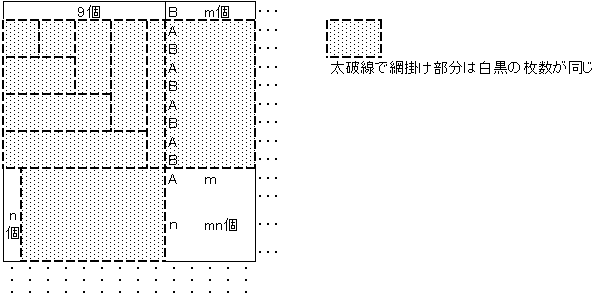
忋偺恾傛傝丄
| 丂 | 俙偑暲傋偨枃悢 | 俛偑暲傋偨枃悢 |
|---|---|---|
| 侾 | 倣値 | 2m亄2n亄4亊1 |
| 俀 | 2m亄2n亄4亊3 | 2m亄2n亄4亊5 |
| 俁 | 2m亄2n亄4亊7 | 2m亄2n亄4亊9 |
| 係 | 2m亄2n亄4亊11 | 2m亄2n亄4亊13 |
| 俆 | 2m亄2n亄4亊15 | 2m亄2n亄4亊17 |
| 寁 | mn亄8(m亄n)亄4亊36 | 10(m亄n)亄4亊45 |
A偺枃悢偺崌寁偲B偺枃悢偺崌寁偑摍偟偄偲偟偰幃傪惍棟偡傞偲丄
丂丂丂mn亖2m亄2n亄4亊9
亪丂(m亅2)(n亅2)亖40
偙偺曽掱幃傪夝偔偲丄
| m-2 | n-2 | m | n | 10(m亄n)亄4亊45 |
|---|---|---|---|---|
| 1 | 40 | 3 | 42 | 630 |
| 2 | 20 | 4 | 22 | 440 |
| 4 | 10 | 6 | 12 | 360 |
| 5 | 8 | 7 | 10 | 350 |
偩偐傜崌寁700枃嵟彮偱偡丅
夝摎丒偦偺10
乮儁儞僱亅儉丗揮埵斀墳乯
敀偺挿曽宍偼丄敀偺惓曽宍偑墶偵俙枃丄廲偵俛枃暲傋偰嶌傜傟偰偄傞傕偺偲偡傞偲丄
偟傑偟傑偺挿曽宍偺堦晹偼丄埲壓偺恾偺傛偆偵昞尰偱偒傞丅
扐偟丄俙亜俛丄壗傟傕惓惍悢丅
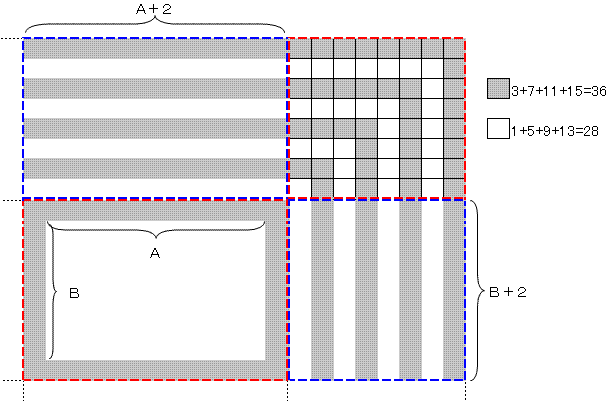
惵怓偺揰慄偱埻傑傟偨偦傟偧傟偺巐妏宍偵偮偄偰丄崟偲敀偺惓曽宍偺悢偼摍偟偄偺偱
愒怓偺揰慄偱埻傑傟偨侾偮偺挿曽宍偲係偮偺惓曽宍(忋恾偱偼丄侾偮偺傒昞帵)偵偮偄偰丄
崟偲敀偺惓曽宍偺悢偑摍偟偄偙偲偑昁梫偱偁傞丅
丂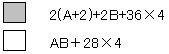
丂丂2(A+2)+2B+36亊4=AB亄28亊4
丂丂傛偭偰丄A=(2B+36)乛(B-2)
B偵悢抣傪戙擖偟偰丄A丄A+B丄AB偵偮偄偰惍棟偡傞偲埲壓偺捠傝丅
丂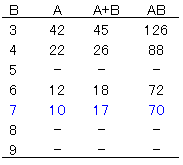
偝偰丄崟偲敀偺惓曽宍偺巻偺崌寁偼丄
丂丂2(A+2)+2B+36亊4亄AB亄28亊4亄16乮A亄2乯+16乮B亄2乯
丂丂=18(A+B)+AB+324
傛偭偰丄戣堄傪枮偨偡偺偼A=10丄B=7側偺偱丄媮傔傞崌寁枃悢偼700
夝摎丒偦偺11
乮儁儞僱亅儉丗MVH乯
巒傔偵A偝傫偑峔惉偟偨挿曽宍傪T偲偟丄T偺廲偺挿偝傪m丄墶偺挿偝傪n偲偟傑偡丅扐
偟丄m亝n偲偟偰傕堦斒惈傪幐偄傑偣傫丅
偝偰丄廲m丄墶n偺挿曽宍偺廃傝傪丄埻傒廔偊偨偲偒偺宍偑偝傜偵戝偒側挿曽宍偲側傞
傛偆偵埻傓乮拲乯偲偒丄埻傓偺偵昁梫側惓曽宍偺巻偺枃悢偼丄2埲忋偺偁傞惍悢偺慻
(p,q)傪梡偄偰丄
丂丂(m+p)(n+q)-mn=mq+np+pq乮枃乯
偲昞偣傑偡丅
偲偙傠偑丄崱丄崟偲敀偺巻偺崌寁偑嵟傕彮側偄応崌傪峫偊偰偄傞偙偲偐傜丄p=q=2偺
偲偒丄戣堄傪枮偨偡慻(m,n)偑懚嵼偡傞側傜偽丄偦傟偑媮傔傞応崌偲側傝傑偡丅
偙偺忦審偺壓偱丄廲m丄墶n偺挿曽宍偺廃傝傪偡偒傑側偔埻傓偲偒丄埻傓偺偵昁梫側惓
曽宍偺巻偺枃悢偼丄
丂丂(m+2)(n+2)-mn=2(m+n+2) = f(m,n)
偲昞偣傑偡丅
傛偭偰丄B偝傫偑5夞埻傒廔偊偨偲偒丄A偝傫丄B偝傫偑巊偭偨巻偺枃悢偼丄偦傟偧傟丄
丂丂A偝傫丗mn+f(m+2,n+2)+f(m+6,n+6)+f(m+10,n+10)+f(m+14,n+14)=mn+8m+8n+144
丂丂B偝傫丗f(m,n)+f(m+4,n+4)+f(m+8,n+8)+f(m+12,n+12)+f(m+16,n+16)=10m+10n+180
偲側傝傑偡丅
戣堄傛傝丄偙偺2偮偼摍偟偄偺偱丄師偺摍幃傪摼丄惍棟偡傞偲丄m亝n傛傝丄
丂丂丂mn+8m+8n+144=10m+10n+180
丂丂佁(m-2)(n-2)=40
丂丂佁(m-2,n-2)=(1,40),(2,20),(4,10),(5,8)
丂丂佁(m,n)=(3,42),(4,22),(6,12),(7,10)
偲側傝傑偡丅
戣堄傪枮偨偡慻(m,n)偑懚嵼偟偨偺偱丄偙偺4慻偺偆偪偱丄敀偲崟偺巻偺崌寁偑嵟彫偺
慻傪媮傔傑偡丅
敀偲崟偺巻偺崌寁偼丄
丂丂(mn+8m+8n+144)+(10m+10n+180)=mn+18m+18n+324=(m+18)(n+18)乮枃乯
偱偡偐傜丄忋婰偺4慻偺偆偪丄偙傟偑嵟彫偵側傞偺偼丄(m,n)=(7,10)偺偲偒偱丄崌寁
偼700枃偱偡丅乮摎偊乯
乮拲乯栤戣暥偵偼丄扨偵乽埻傓乿偲偁傝傑偡偺偱丄偳偺傛偆偵埻傫偱傕椙偄傕偺偲夝
庍偱偒傑偡丅偟偐偟丄栤戣偺戣柤乽偟傑偟傑偺挿曽宍乿偐傜丄偙偺傛偆偵峫偊傑偟
偨丅
乲夝偒廔偊偰乴
挿曽宍傪乽埻傓乿偲偄偆昞尰偑濨枂偱丄擮偺偨傔丄忋婰偺傛偆側夝摎偵偟傑偟偨丅偦
傟傪彍偗偽丄昁梫忦審偱媫懍偵岓曗傪峣傟傞杮栤偼丄堄奜偱柺敀偐偭偨偱偡丅
夝摎丒偦偺12
乮儁儞僱亅儉丗T_Tatekawa乯
椺偊偽A偝傫偑 1x2 偱挿曽宍傪嶌偭偨応崌丆埲壓偺傛偆偵側傝傑偡丏
仩仩 仭仭仭仭 仭仩仩仭 仭仭仭仭 仩仩仩仩仩仩 仩仭仭仭仭仩 仩仭仩仩仭仩 仩仭仭仭仭仩 仩仩仩仩仩仩嵟弶偵敀偑 1x2 =2 枃
師偵崟偑 (1+1) x2 + (2+1)x2 =10 枃
師偵敀偑 (1+3) x2 + (2+3)x2 =18 枃
師偵崟偑 (1+5) x2 + (2+5)x2 =26 枃
...
偲偄偆傛偆偵側傝丆嵟廔揑偵
敀丗2 + 18 + 34 + 50 + 66 =170 枃
崟丗10 + 26 + 42 + 58 + 74 = 210 枃
偲側傝傑偡丏
偝偰丆敀偑嵟弶偵傕偟廲M枃暘丆墶N枃暘偺惓曽宍傪暲傋偨偲偟傑偡丏
庢傝埻傓偺偵昁梫側崟偺惓曽宍偺枃悢偼
丂丂(M+1) x2 + (N+1)x2 = 2x(M+N) +4 枃
偱偡丏忋偺椺偱傕傢偐傞傛偆偵丆屻偼奜傪暍偆怓偺惓曽宍偺枃悢偼丆
偡偖撪懁偺怓偺惓曽宍偺枃悢傛傝傕8枃懡偔側傝傑偡丏
傛偭偰丆擇弰栚埲崀偺敀偲崟偺枃悢偺嵎偼丆崟偺曽偑 8x4=32枃懡偔側傝傑偡丏
崟偲敀偺巊梡枃悢偑摨偠偵側傞偲偄偆偙偲偼丆
丂丂M x N = 2x(M+N) + 4 + 32
丂丂M x N - 2 x (M+N) = 36
丂丂(M-2)(N-2) = 40
偙傟傪枮偨偡帺慠悢 M, N 偺慻偼 M 亙 N 偲偟偰
(3, 42), (4, 22), (6, 12), (7, 10) 偺4捠傝丏
敀丆崟偺慡巊梡枃悢偼
敀丗 M x N + 4x (2x(M+N) +4) +(8+24+40+56)
=M x N + 8x(M+N) + 144
崟丗 5x (2x(M+N) +4) +(16+32+48+64)
= 10x(M+N) + 180
(M, N)= (3, 42) 偺帪 630枃
(M, N)= (4, 22) 偺帪 440枃
(M, N)= (6, 12) 偺帪 360枃
(M, N)= (7, 10) 偺帪 350枃
傛偭偰丆崟偲敀偺巻偺崌寁偑嵟傕彮側偄応崌偼丆350 x 2 = 700 枃
夝摎丒偦偺13
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂俈侽侽枃巊梡偟傑偡丅
拞怱偺挿曽宍偺奜廃傪倃丄倄偲偡傞偲師偺幃偑惉傝棫偪傑偡丅
敀偺奜廃丂(1)丂俀乮倃亄俀乯亄俀乮倄亄俀乯亖俀乮倃亄倄乯亄俉
崟偺奜廃丂(1)丂俀乮倃亄係乯亄俀乮倄亄係乯亖俀乮倃亄倄乯亄16
敀偺奜廃丂(2)丂俀乮倃亄俇乯亄俀乮倄亄俇乯亖俀乮倃亄倄乯亄24
崟偺奜廃丂(2)丂俀乮倃亄俉乯亄俀乮倄亄俉乯亖俀乮倃亄倄乯亄32
敀偺奜廃丂(3)丂俀乮倃亄10乯亄俀乮倄亄10乯亖俀乮倃亄倄乯亄40
崟偺奜廃丂(3)丂俀乮倃亄12乯亄俀乮倄亄12乯亖俀乮倃亄倄乯亄48
敀偺奜廃丂(4)丂俀乮倃亄14乯亄俀乮倄亄14乯亖俀乮倃亄倄乯亄56
崟偺奜廃丂(4)丂俀乮倃亄16乯亄俀乮倄亄16乯亖俀乮倃亄倄乯亄64
敀偺奜廃丂(5)丂俀乮倃亄18乯亄俀乮倄亄18乯亖俀乮倃亄倄乯亄72
崟偺奜廃丂(5)丂俀乮倃亄20乯亄俀乮倄亄20乯亖俀乮倃亄倄乯亄80
崟偺嵟廔偺奜廃偱敀偺巊梡枃悢偵側傞偵偼俉亊俆偱摨偠偵側傟偽椙偄偺偱偡
嵟屻偺廃偺挿偝偼偦傟偧傟侾侽廃側偺偱俀亊侾侽亖俀侽傪壛偊偨傕偺偱偡丅
廬偭偰丄
乮俆亄俀侽乯亄乮俉亄俀侽乯亖俀俆亊俀俉亖俈侽侽偲側傝傑偡丅
夝摎丒偦偺14
乮儁儞僱亅儉丗偺偭偙傫乯
侾乯偡傋偰堦廳偵姫偔帪
丂丂侾夞栚丂丂a*b (a,b偼惍悢丄1亝a亝b) 偺挿曽宍傪嶌傞丂丂丂暲傋傞巻偺悢偼ab
丂丂俀夞栚 (a+2)*(b+2) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂(a+2)(b+2)-ab=2a+2b+4 仼暲傋傞巻偺悢
丂丂俁夞栚丂丂(a+4)*(b+4) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂(a+4)(b+4)-(a+2)(b+2)=2a+2b+12 仼暲傋傞巻偺悢
丂丂係夞栚丂丂(a+6)*(b+6) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂暲傋傞巻偺悢偼丂2a+2b+20
丂丂俆夞栚丂丂(a+8)*(b+8) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂暲傋傞巻偺悢偼丂2a+2b+28
丂丂俇夞栚丂丂(a+10)*(b+10) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂暲傋傞巻偺悢偼丂2a+2b+36
丂丂俈夞栚丂丂(a+12)*(b+12) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂暲傋傞巻偺悢偼丂2a+2b+44
丂丂俉夞栚丂丂(a+14)*(b+14) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂暲傋傞巻偺悢偼丂2a+2b+52
丂丂俋夞栚丂丂(a+16)*(b+16) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂暲傋傞巻偺悢偼丂2a+2b+60
丂侾侽夞栚丂丂(a+18)*(b+18) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂暲傋傞巻偺悢偼丂2a+2b+68
丂侾侾夞栚丂丂(a+20)*(b+20) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂暲傋傞巻偺悢偼丂2a+2b+76
丂侾俀夞栚丂丂(a+22)*(b+22) 偺挿曽宍偵偡傞
丂丂丂丂丂丂丂丂暲傋傞巻偺悢偼丂2a+2b+84
丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
3夞栚偲4夞栚丄5夞栚偲6夞栚丄7夞栚偲8夞栚丄9夞栚偲10夞栚偱偼丄忢偵崟偑俉枃懡偄偺偱
丂丂丂ab=8*4+2a+2b+4
丂丂丂(a-2)(b-2)=40
嵟彫傪峫偊偰偄傞偐傜 a-2=5 b-2=8 傪偲偭偰 a=7 b=10
偙偺帪崟偺枃悢偼 10(a+b)+180=350丂偩偐傜
崌寁偼 700 枃
俀乯擇廳傪1夞嫋偡偙偲偺専摙
擇廳偵姫偔偙偲傪嬛偠偰偄側偄傛偆側偺偱擇廳傪1夞嫋偟偰
700 枃埲壓偑壜擻偐偳偆偐専摙偡傞
擇廳傪1夞嫋偡偲嵟屻偼 (a+20)*(b+20) 偺挿曽宍偵側傞
丂(a+20)(b+20)亝700 偼
丂a=1 偺帪偼丂2亝b亝13丄a=2 偺帪偼丂3亝b亝11丄a=3 偺帪偼 4亝b亝10丄
丂a=4 偺帪偼 5亝b亝9丄a=5 偺帪偼丂6亝b亝8丂偱偁傟偽枮偨偝傟傞偐傜廫暘専摙偵抣偡傞
丂(1)俁夞栚乮敀偺俀夞栚乯傪擇廳偵偡傞
丂丂ab+4a+4b+32=8*3+4a+4b+32
丂丂ab=24
丂丂嵟彫傪峫偊偰偄傞偐傜 a=4 b=6 傪偲傞
丂丂偙偺帪崟偺枃悢偼 10(a+b)+212=312
丂丂傛偭偰崌寁偼 624 枃
丂(2)俆夞栚乮敀偺俁夞栚乯傪擇廳偵偡傞
丂丂ab+4a+4b+64=8*3+4a+4b+48
丂丂ab=8
丂丂嵟彫傪峫偊偰偄傞偐傜 a=2 b=4 傪偲傞
丂丂偙偺帪崟偺枃悢偼 10(a+b)+204=264
丂丂傛偭偰崌寁偼 528 枃
丂(3)擇廳傪侾夞嫋偟偰崌寁偑 700 枃埲壓偵側傞偺偼埲忋偺俀偮偺応崌偩偗偱偁傞
俁乯嶰廳傪侾夞嫋偡乮擇廳傪俀夞嫋偡乯偙偲偺専摙
丂嶰廳傪侾夞嫋偟偰丄偁傞偄偼擇廳傪俀夞嫋偟偰 528 枃埲壓偑壜擻偐偳偆偐専摙偡傞
丂偦偺傛偆偵偡傞偲嵟屻偼 (a+22)*(b+22) 偺挿曽宍偵側傞偑
丂丂
丂(a+22)(b+22)亝528 傪枮偨偡 a,b 偼懚偟側偄
埲忋傛傝丄巻偺崌寁偼嵟傕彮側偄応崌偱 528 枃
夝摎丒偦偺15
乮儁儞僱亅儉丗haya乯
崟偲敀偺巻偺崌寁偼丄嵟傕彮側偄応崌偵 420 枃偱偡丅
亂夝偒曽亃
撪懁偐傜奜懁偵岦偐偭偰挿曽宍偺椞堟傪丄A1 仺 B1 仺 A2 仺 B2 仺 A3 仺 B3 仺 A4 仺 B4 仺 A5 仺 B5 偲柤晅偗傞丅
偙偺栤戣偼敀偺晄懌傪偳偆曗懌偟偰摨悢偵偡傞偐偲偄偆栤戣偱偡偑丄愭偢丄扨弮偵 A1 偺傒偱曗偄丄B1 埲崀偼暆1偺嵟彫偺岤傒偺挿曽宍偱暍偭偨傜
偳傫側恾宍偵側傞偐傪寁嶼偟偰傒傑偟偨丅
偦傟偑壓恾 Fig.1 偱丄A1 偼 7x10 丄慡懱偼 25x28=350x2=700 偱偟偨丅
Fig.1

偙傟傪娤嶡偟偰丄A1 偺傒傪戝偒偔偡傞曽朄偼慡懱偑戝偒偔側傞僨儊儕僢僩偑偁傞偺偱嵟彮夝傪摼傞彆偗偵偼側傜傫偩傠偆偲巚偄傑偟偨丅
媡偵 A5 偺傛偆側奜廃偵嬤偄晹暘傪乽曃擏乿偵偟偰敀偺晄懌傪曗偆曽偑棟偵揔偭偰偄傞偲嶼弍揑偵梊應偟傑偟偨丅
偦偙偱崱搙偼 A1 傪嵟彫偺 1x1 偲偡傞偲偟偰丄偙傟傕傑偨夝偵娭學側偔暆侾偺嵟彫偺挿曽宍偱杽傔偨恾宍傪嶌恾偡傞偲 Fig.2 偺傛偆偵 19x19 偲側傝傑偡丅
Fig.2

媮傔傞嵟彮夝偼 Fig.2 傛傝彫偝偔側傞偙偲偼偁傝傑偣傫偐傜丄19x20丄20x20丄20x21丒丒丒偺傛偆偵
徃弴偵嵟彫側夝傪扵偣偽傛偄偲峫偊傑偟偨丅
偲偙傠偑丄19x20丄20x20丄偱偼嵟傕桳棙側 A4 偺擏岤傪嵟戝偵偟偰傕敀偺晄懌傪僇
僶乕偱偒傑偣傫偐傜晄壜丅
20x21 偱帋峴嶖岆偟偰丄 Fig.3 偺傛偆側媮傔傞嵟彫恾宍傪摼傑偟偨丅
20x21=210x2=420 枃偑摎偊偵側傝傑偡丅
Fig.3

彯丄A1傪乽傑偢敀偺巻傪偡偒傑側偔側傜傋偰挿曽宍傪偮偔傝傑偡乿偺
乽挿曽宍乿偵峉偭偨応崌偺夝偼 Fig.4 偱丄枃悢偼 20x22=220x2=440 枃偱偡丅
Fig.4

惓夝幰
| 柪巕偺梇擫 | 栭傆偐偟偺偮傜偄偍偠偝傫 | teki |
| 揮埵斀墳 | 僗儌乕僋儅儞 | 偺偭偙傫 |
| haya | falcon@拞妛嫵巘 | 僆儎僕 |
| 偄偲偆傂傠備偒 | ykak | 忨偺偍偠偝傫 |
| T_Tatekawa | 嶰妏掕婯 | MVH |
僐儊儞僩
嵟弶偺挿曽宍偼椺奜偱偡偑丄偦傟埲崀偼岞嵎俉偺摍嵎悢楍偵側傝傑偡偐傜丄
偦傟傪婎偵丄敀丒崟偦傟偧傟昁梫側枃悢傪媮傔偰曽掱幃傪棫偰傟偽傛偄偙偲偑傢偐傝傑偡丅
偟偐偟丄曽掱幃傪夝偐側偔偰傕傛偄曽朄偑偁傝傑偡丅
敀崟偺弴偱峫偊傟偽丄崟偑俉枃懡偔丄偦傟偑俆僒僀僋儖偱係侽枃丅偙傟傪偼偠傔偺挿曽宍偱
傑偐側偊偽傛偄偺偱丅廲亊墶亖係侽偺挿曽宍傪嬦枴偡傞偲傛偄偱偡偹丅
偲偙傠偱丄壗恖偐偺曽偵偛幙栤丄傕偟偔偼偛夝摎偄偨偩偄偰偄傑偡偑丄 敀丄崟偺巻偱偡偒傑側偔埻傓帪偵丄埫栙偺偆偪偵侾廳偲峫偊偰偄傑偨偑丄 栤戣暥偐傜偩偲丄偦偆偲傕尷傝傑偣傫偹丅俀廳丄俁廳傪嫋偡偲丄夝摎偺壜擻惈偑峀偑傝傑偡丅 偺偭偙傫偝傫丄haya偝傫 偙傟傜偵偮偄偰傕峫嶡傪偄偨偩偒丄偳偆傕偁傝偑偲偆偛偞偄傑偟偨丅
 top
top