Challenge!

問題163　ある関数の問題
Weekend Mathematics／問題／問題163　ある関数の問題

問題163　ある関数の問題

整数から整数への関数 f が、

　　　f ( n ) = n - 3　　　 　 　 　(n≧1000のとき）
　　　　　 　 = f ( f ( n + 5 ) )　 (n＜1000のとき）

をみたすとき、f ( 163 ) を求めよ。

問題の出典

ジュニア数学オリンピック 米国選抜数学試験 (1984) 改題
ジュニア数学オリンピック2003-2008
数学オリンピック財団編
日本評論社

答えと解説

解答・その1

（ペンネ－ム：浜田　明巳）

エクセルのマクロで再帰関数を作りました．答は998です．
ｎ≦1001で998と997が交互に出て来るのが面白いですね．

 Option Explicit
Sub Macro1()
    Dim j As Integer
    For j = 1 To 1000 + 10
      Cells(j, 1).Value = f(j)
      Range("A" & j).Select
    Next j
    Range("A163").Select
End Sub
Private Function f(ByVal n As Integer) As Integer
    If n >= 1000 Then
      f = n - 3
    Else
      f = f(f(n + 5))
    End If
End Function


解答・その2

（ペンネ－ム：転位反応）

具体的に数値を代入して書き出してみる。

　　f(163)=f(f(168))
　　f(168)=f(f(173))
　　・
　　・
　　・
　　f(993)=f(f(998))
　　f(998)=f(f(1003))=f(1000)=997

その結果、f(998)の値を確定できることが判明、その値をf(993)=f(f(998))の式に代入して、 f(993)の値も算出でき、順次、f(163)まで溯れば求める値を算出できるものと推察できる。 実際に計算してみる。

　　f(998)=f(f(1003))=f(1000)=997
　　f(993)=f(f(998))=f(997)=f(f(1002))=f(999)=f(f(1004))=f(1001)=998
　　f(988)=f(f(993))=f(998)=997
　　f(983)=f(f(988))=f(997)=998
　　f(978)=f(f(983))=f(998)=997
　　f(973)=f(f(978))=f(997)=998
　　・
　　・
　　・

以上より、

　　f(993)=f(983)=f(973)=・・・=f(997)=998

163=993-10×83　であることから
　　f(163)=f(993-10×83)=f(997)=998

∴f(163)=998

解答・その3

（ペンネ－ム：スモークマン）

f(163)=f(f(163+5))=....=f(f(f(...f(998)...)))
f(998)=f(f(1003))=f(1000)=997
f(997)=f(f(1002))=f(999)=f(f(1004))=f(1001)=998
つまり...
998=163+5*167
f の数は...167という奇数なので...
167番目のf(998)→166番目のf(997)→165番目のf(998) になり...
奇数個目となる1番目はf(998)なので...
f(163)=f(f(998))=f(997)=998

解答・その4

（ペンネ－ム：falcon@中学教師）

＜答え＞
　ｆ(163)＝998
＜考え方＞
ｆ(1000)から調べていくことにしました。
　ｆ(1000)＝997
　ｆ(999)＝ｆ(ｆ(1004))＝ｆ(1001)＝998
　ｆ(998)＝ｆ(ｆ(1003))＝ｆ(1000)＝997
　ｆ(997)＝ｆ(ｆ(1002))＝ｆ(999)＝998
　ｆ(996)＝ｆ(ｆ(1001))＝ｆ(998)＝997
　ｆ(995)＝ｆ(ｆ(1000))＝ｆ(997)＝998
　ｆ(994)＝ｆ(ｆ(999))＝ｆ(998)＝997
　ｆ(993)＝ｆ(ｆ(998))＝ｆ(997)＝998
　　・
　　・
　　・
上記の結果より、n＜1000のときにおいては、
　n＝奇数ならばｆ(n)＝998、
　n＝偶数ならばｆ(n)＝997と予想できる。
これに基づいて考えると、163は奇数なので、ｆ(163)＝998。

解答・その5

（ペンネ－ム：haya）

f ( 163 ) の値は 998 です。

【解き方】
　　f(1004) = 1001
　　f(1003) = 1000
　　f(1002) = 999
　　f(1001) = 998
　　f(1000) = 997
以下、上を使って、
　　f(999) = f(f(1004)) = f(1001) = 998
　　f(998) = f(f(1003)) = f(1000) = 997
　　f(997) = f(f(1002)) = f(999) = 998
　　f(996) = f(f(1001)) = f(998) = 997
　　・・・
となり、後は 998 と 997 を往復するだけ。

解答・その6

（ペンネ－ム：杖のおじさん）

答え　９９８　です
ｎが１０００未満なので1000以下から計算をして見ます。
　　(1) f(999)=f(f(1004)=f(1001)=998
　　(2) f(998)=f(f(1003)=f(1000)=997
　　(3) f(997)=f(f(1002)=f(999)=998
　　(4) f(996)=f(f(1001)=f(998)=997
　　(5) f(995)=f(f(1000)=f(997)=998
　　(6) f(994)=f(f(999)=f(996)=997
　　(7) f(993)=f(f(998)=f(995)=998
　　(8) f(992)=f(f(997)=f(994)=997
　　(9) f(991)=f(f(996)=f(993)=998
　　(10) f(990)=f(f(995)=f(992)=997
　　(11) f(989)=f(f(994)=f(991)=998
　　(12) f(988)=f(f(993)=f(990)=997
　　(13) f(987)=f(f(992)=f(989)=998
　　(14) f(986)=f(f(991)=f(988)=997
　　・ 　・　　・　　　・　・
　　・ 　・　　・　　　・　・
　　　f(163)=f(f(168))=f(165)=998

(1)～(14)までの計算の結果f(n)のnが奇数の場合は９９８、偶数の場合は９９７であることが推測できます。
上記の計算によると986≦n＜1000の間で正しいと分かります。

986以下の整数をaとして　a＜nに対して正しいと仮定すると
aが奇数ならばa+5は 1000未満の偶数だからf(a)=f(f(a+5))=f(a+2)=998となります。
aが偶数ならばa+5は1000未満の奇数だからf(a)=f(f(a+5))=f(a+2)=997となります。
従ってn=aに対しても推測は正しいと判断します。
以上によりすべてのn＜1000なるものにこの推測が正しいと判断します。

問題のnは163（奇数）なので
f(163)=f(f(168))=f(165)=998

答えは９９８となります。

解答・その7

（ペンネ－ム：のっこん）

999+5=1004 だから
f(1004)～f(1000) の値を求める

　　f(1004)=1001
　　f(1003)=1000
　　f(1002)= 999
　　f(1001)= 998
　　f(1000)= 997

これをもとに、n＜1000 の時の値を求める

　　f(999)=f(f(1004))=f(1001)= 998
　　f(998)=f(f(1003))=f(1000)= 997
　　f(997)=f(f(1002))=f( 999)= 998
　　f(996)=f(f(1001))=f( 998)= 997
　　f(995)=f(f(1000))=f( 997)= 998
　　f(994)=f(f( 999))=f( 998)= 997
・・・・・・・・・・・・・・・・・・・

n≦1001 の時、
　　n が奇数→f(n)=998
　 n が偶数→f(n)=997 となるから f(163)=998


解答・その8

（ペンネ－ム：teki）

答え　９９８

ｆ（１０００）から追いかけると、
ｆ＜１０００において
　　ｎが奇数のとき、ｆ（ｎ）＝９９８
　　ｎが偶数のとき、ｆ（ｎ）＝９９７
となります。
よって、ｆ（１６３）＝９９８

解答・その9

（ペンネ－ム：オヤジ）

ｎにｆ(　)をｍ回施したものを下記の様に表す。
　　ｆ(m)(ｎ)＝ｆ(ｆ(ｆ(・・・(ｎ)・・・)))　　但し　ｆ(ｎ)＝ｆ(1)(ｎ)
　※　５ｍ＋１５８　が１０００以上となるｍの最小値は、ｍ＝１６９



∴　ｆ(１６３)＝９９８

解答・その10

（ペンネ－ム：T_Tatekawa）

n=1000 付近の値を見てみます．
　　f(1004)=1001
　　f(1003)=1000
　　f(1002)=999
　　f(1001)=998
　　f(1000)=997

　　f(999)=f(f(1004))=f(1001)=998
　　f(998)=f(f(1003))=f(1000)=997
　　f(997)=f(f(1002))=f(999)=998
　　f(996)=f(f(1001))=f(998)=997
　　f(995)=f(f(1000))=f(997)=998

これを踏まえて計算します．以下，

　f<3> (a) = f(f(f(a)))

というように，fが多重に入り込む時の略記法 fを使う事にします．

　(1003-163)/5 = 168

なので

　f(163) = f<169>(1003) = f<168>(1000) = f<167>(997)

です．

　f(f(997)) = f(998) = 997

なので，二重の f がかかると 997 は元にもどります．よって，

　f(163) = f<167>(997) = f(997) = 998

となります．

解答・その11

（ペンネ－ム：SOU）

事前準備
m個の関数fの合成を
　f(f(・・・f(f(n))・・・))) = fm(n)
のように、まとめて書くようにします。
　即ち前提条件の
　f(n) = f(f(n+5) 　を 　f(n) = f2(n+5) 　とあらわします。なお、
　f(n) = n-3 　 (n≧1000)・・・(1)
　f(n) = f2(n+5) (n＜1000)・・・(2)
　と番号をつけておきます。
　(2)は繰り返し使うことにより、
　f(n) = fk(n+5*k) (n＜1000)
　とできることを意味します。

　f1(163) 
　 = f1+168(163+5*168)      　 (2)を適用
　 = f169(1003)           ★
　 = f168(1000)                (1)を適用
 　= f167(997)                 (1)を適用
 　= f168(1002)              　(2)を適用
 　= f167(999)                 (1)を適用
　 = f168(1004)                (2)を適用
　 = f167(1001)                (1)を適用
　 = f166(998)                 (1)を適用
　 = f167(1003)           ☆   (2)を適用
この時点で☆と★を見ると、
「引数の値を変えずに合成された関数の数を2個減らすことが出来る」
ことがわかります。
ただし、★から☆への過程で最大3つ減る状態があるので
　fm(n) => fm-2(n) (m＞3)
という制限がつきます。 以上のことから、
　f167(1003)
　 = f3+2*82(1003)
   = f3(1003)
   = f2(1000)
   = f1(997)
   = f2(1002)
   = f1(999)
   = f2(1004)
   = f1(1001)
   = 998


解答・その12

（ペンネ－ム：シュレーディンガーの三毛猫）

【答】998

【解法】
簡便のため、関数f(n)をnに対してp回作用させることを f[p](n)と記すことができるものとする。 例えば、
　　　f[1](n)＝f(n)
　　　f[3](n)＝f(f(f(n)))
このとき、与えられた関数f(n)は
　　　f(n)＝n-3 　　　　　　(n≧1000)　・・・(1)
　　　　　＝f[2](n+5) (n＜1000)　・・・(2)
と表せる。

(2)より、n+5＜1000のとき
　　　f(n+5)＝f(f(n+10))＝f[2](n+10)
なので、これを(2)の右辺に代入してf(n)は
　　　f(n)＝f(f(f(n+10)))＝f[3](n+10)
となる。
一般に、nが1000より小さく、ある自然数mを用いて
　　n+5(m-1)＜1000
　　n+5m　　≧1000
の両方を満たすとき、上記の操作を繰り返すことでf(n)は、
　　f(n)＝f[m+1](n+5m)　　・・・(3)
と表すことができる。

さて、n＝163のときはm＝168とすれば
　　　163＋5×167＝998　＜1000
　　　163＋5×168＝1003 ≧1000
を満たすので、(3)および(1)よりf(163)は
　　f(163)＝f[169](1003)
　　　　　＝f[168](1000)
　　　　　＝f[167](997)　・・・(4)
となる。

ここで、
　　f(997)＝f[2](1002)
　　　　　＝f(999)
　　　　　＝f[2](1004)
　　　　　＝f(1001)
　　　　　＝998

　　f(998)＝f[2](1003)
　　　　　＝f(1000)
　　　　　＝997

となるので、これらを(4)に代入して、
　　f(163)＝f[167](997)
　　　　　＝f[166](998)
　　　　　＝f[165](997)
　　　　　＝f[164](998)
　　　　　・・・・・
　　　　　＝f[3](997)
　　　　　＝f[2](998)
　　　　　＝f[1](997)
　　　　　＝998

よって、解は998と求まる。

解答・その13

（ペンネ－ム：夜ふかしのつらいおじさん）

f(163)=998 です。

nが1000以上の場合は、直ぐに関数の値が分かります。
nが1000より小さい場合、直ぐには値は分かりません。

f(999)からf(995)について、調べてみます。
　　f(999)=f(f(1004))=f(1001)=998
　　f(998)=f(f(1003))=f(1000)=997
　　f(997)=f(f(1002))=f(999)=998（上の結果より）
　　f(996)=f(f(1001))=f(998)=997（上の結果より）
　　f(995)=f(f(1000))=f(997)=998（上の結果より）

次に、f(994)からf(990)について、調べてみます。
その際、上の５つの結果を使います。

　　f(994)=f(f(999))=f(998)=997
　　f(993)=f(f(998))=f(997)=998
　　f(992)=f(f(997))=f(998)=997
　　f(991)=f(f(996))=f(997)=998
　　f(990)=f(f(995))=f(998)=997

ｎの値を10少なくした場合を考えます。
989から985の場合は、994から990の部分を参照します。
例えば、f(986)=f(f(991))=f(998)=997

984から990の場合は、989から985の部分を参照します。
例えば、f(983)=f(f(988))=f(997)=998

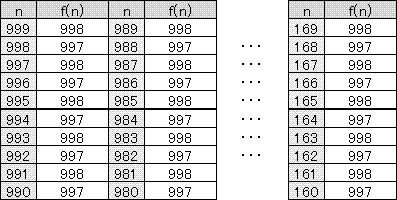
これらの結果を表にすると、次のようになります。
nを下げていくとき同じ仕組みが繰り返されます。
nが偶数の場合は997、奇数の場合は998となります。




解答・その14

（ペンネ－ム：ykak）

答え　　998

考え方
(1)　問題の関数を値が分かりやすい n = 1000 のあたりから小さい方に計算してみる。
以下では　f( f( n ))をf f( n )と表記する。
　　　f( 1000 ) = 1000 - 3 = 997
　　　f( 999 ) = f f( 1004 ) = f( 1004 - 3 ) = f( 1001 ) = 1001 - 3 = 998
　　　f( 998 ) = f f( 1003 ) = f( 1003 - 3 ) = f( 1000 ) = 997
　　　f( 997 ) = f f( 1002 ) = f( 1002 - 3 ) = f( 999 ) = 998
　　　f( 996 ) = f f( 1001 ) = f( 1001 - 3 ) = f( 998 ) = 997
　　　f( 995 ) = f f( 1000 ) = f( 997 ) = 998

このように、n が 999 から 995 までは、
　　　n が奇数の場合は f( n ) = 998
　　　n が偶数の場合は f( n ) = 997 になる。―― X

(2)　次に n が 994 より小さい場合を考える。
f( n ) = f f( a ) とすると（ ただし a = n + 5 ）、 n = 994 のとき、a = 999 だが、a は n より大きいから、この場合 f( a ) は(1)で計算 した通り決まっており、上記のX から a が奇数の場合 f( a ) は 998 である。 従って、f( n ) = f( 998 ) = 997 である。
そうすると、この場合も、n が偶数であれば f( n ) は 997 になると言える。 ―― Y
同様に n = 993 の場合、a = 998 で偶数だから、X より f( a ) は 997 となり、
　　　f( n ) = f( 997 ) = 998 である。
従って、この場合も、n が奇数であれば f( n ) = 998 になると言える。―― Z
(3)　以下順次 n を小さくして f( n ) の値を同様に決めて行くことができるが、 上記の X,Y,Z から、それらのすべてについて、
　　　n が偶数の場合は f( n ) = 997
　　　n が奇数の場合は f( n ) = 998
になる事が分かる。
問題は n が163 のときの f( n ) の値ということであるが、163は奇数だから、f( n ) は 998 になる。

解答・その15

（ペンネ－ム：abc）

「n≦1001をみたすすべての整数nについて、nが奇数のときf(n)=998,ｎが偶数のときf(n)=997となる」…（＊）
ことを数学的帰納法で証明する。

f(n)の定義より　[f(1001)=998,f(1000)=997,f(999)=998,f(998)=997,f(997)=998]…(1)

[f(k)=998,f(k-1)=997 ,f(k-2)=998,f(k-3)=997,f(k-4)=998　（ただし、kは奇数でk≦1001)
が成り立つと仮定すると、
f(k-5)=f(f(k))=f(998)=997,f(k-6)=f(f(k-1))=f(997)=998]…(2)
(1)、(2)、より（＊）が示された。

よって、f(163)=998…(答）

解答・その16

（ペンネ－ム：MVH）

結論から述べると、f(163) = 998 である。
さて、次（☆）が言える。
自然数に対して、
　　f(1000-2k+1) = 998
　　f(1000-2k) = 997
である（☆）。

以下では、これを自然数に関する降下帰納法により示す。
ⅰ）k=1 のとき、
　　f(999) = f(f(1004)) = f(1001) = 998
　　f(998) = f(f(1003)) = f(1000) = 997
より、成立。

ⅱ）k=2 のとき、
　　f(997) = f(f(1002)) = f(999) = 998
　　f(996) = f(f(1001)) = f(998) = 997
より、成立。

ⅲ）k=3 のとき、
　　f(995) = f(f(1000)) = f(997) = 998
　　f(994) = f(f(999)) = f(998) = 997
より、成立。

ⅳ）k(≧3)以下での成立を仮定する。このとき、

　　

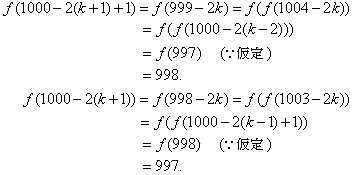
より、k+1 でも成立。

以上ⅰ）～ⅳ）により、自然数で☆が成立することが言えた。
結局、冒頭の結論、f(163) = 998 を得る。

正解者

浜田　明巳 オヤジ のっこん
夜ふかしのつらいおじさん T_Tatekawa 転位反応
スモークマン teki abc
ykak シュレーディンガーの三毛猫 杖のおじさん
falcon@中学教師 SOU haya
MVH

コメント

f(163)=f(f(168))=f(f(f(173)))=f(f(f(f(178))))=・・・
というように、1000に満たない整数を代入すると、関数の入れ子状態になっていきます。
（関数の値をまたその関数で定義するものを再帰関数と言ったりしますね。）
ところが、1000以上になると、n-3で定義されますから、この近辺で、言わば、 いったりきたりの現象が見られます。
結果的に、nが偶数の場合と奇数の場合とで、異なる結果に帰着されます。

top