問題162 平方数の問題
相異なる３つの正整数の組であって、どの２つの和も平方数になるようなもののうち、
３数の和が最小になる組合せを求めてください。
問題の出典
第４回ジュニア数学オリンピック(2006)
ジュニア数学オリンピック2003-2008
数学オリンピック財団編
日本評論社
答えと解説
解答・その1
（ペンネ−ム：エルドス）
有効桁数の関係で数学的とは思えませんが、シンプルな解答なのでいかがでしょうか。
これも正解？
2数の和の平方根が整数⇔2数の和の平方根とそれを整数化（切り捨て）したものが等しい。
１０進BASICのプログラム
CLEAR
FOR i=1 TO 60
FOR j=i+1 TO 60
FOR k=j+1 TO 60
IF INT((i+j)^0.5)=(i+j)^0.5 AND INT((j+k)^0.5)=(j+k)^0.5 AND INT((k+i)^0.5)=(k+i)^0.5 THEN PRINT i+j+k,i,j,k
NEXT k
NEXT j
NEXT i
END
出力結果
83 2 34 47 85 4 21 60 69 5 20 44 55 6 19 30 97 16 33 48
１から６０までの全ての組合せを調べた結果、３数の和は５５が最小となった。
（５５＜６０より、６０以上の数について調べる必要はない）
解答・その2
（ペンネ−ム：浜田 明巳）
Ｃ＋＋で解きました．
答は（５５＝）６＋１９＋３０です．
複数組の和の表し方にも対応したプログラムです．
パソコン部の顧問をやっていると，情報オリンピックやパソコン甲子園に参加する為に
どうしてもＣやＣ＋＋の言語に精通する必要があります．大変ですがいつも勉強しています．
// wm162.cpp #include#include #include #define max 1000 int heihou(int n); void main() { int wa, n1, n2, n3; int deta=0; wa=1+2+3; while(deta==0 && wa < =max) { for(n1=1; n1 < wa; n1++) { for(n2=n1+1; n2 < wa; n2++) { n3=wa-n1-n2; if(n2 < n3) { if(heihou(n1+n2)+heihou(n2+n3)+heihou(n3+n1)==3) { cout << wa << ":" << n1 << "," << n2 << "," << n3 << endl; deta=1; } } } } wa++; } getch(); } int heihou(int n) { int sqr_n; sqr_n=sqrt((double)n); return (sqr_n*sqr_n==n); }
解答・その3
（ペンネ−ム：haya）
相異なる３つの正整数の組で、どの２つの和も平方数になるようなもののうち、３数の和が最小になる組合せは、
6, 19, 30 です。
【解き方】
取り敢えず 102 までの平方を列記する。
その下に、1〜 n2-1 の数字を並べると、例えば、１ と n2-1 の組が和が平方数に
なるような組合せとなる。 ここから、なるべく左寄りに 3 列を選び、更にその列の中で適当な 3 行を選んで
3 つの異なる数が指定されるように選べれば解となる。
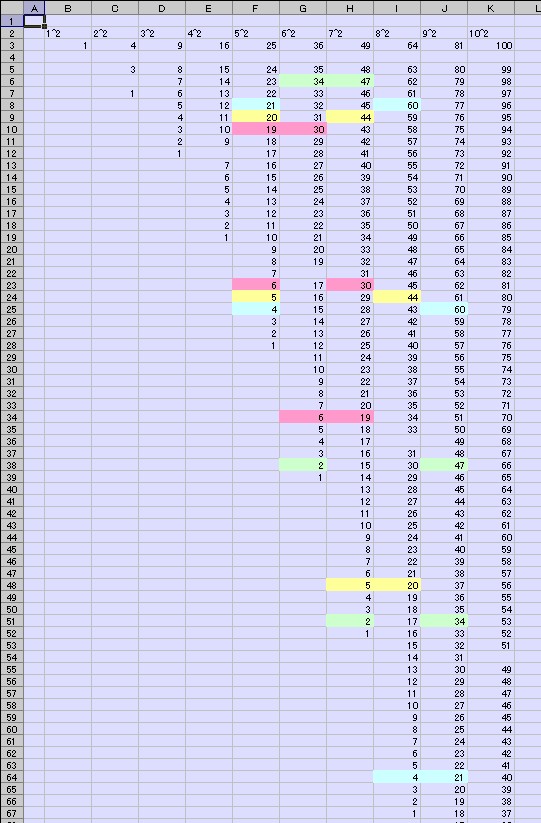
例えば、
マゼンダ色の 6, 19, 30
がそれ。 その他に、
黄色の 5, 20, 44
黄緑の 2, 34, 47
水色の 4, 21, 60など。
Excel のマクロで、次のようなものもありかと・・・。 後は和を求める列を作りソートして最小の組合せを探す。
Option Explicit
'互いに和が平方数になる三つ組みの整数を求める
Sub TernionSqVal()
Dim i As Integer, j As Integer, k As Integer
For i = 1 To 1000
For j = i + 1 To 1000
If Sqr(i + j) = Int(Sqr(i + j)) Then '平方値が整数になっているか
For k = j + 1 To 1000
If Sqr(i + k) = Int(Sqr(i + k)) And _
Sqr(j + k) = Int(Sqr(j + k)) Then
'3列に書き出す
ActiveCell.Value = i
ActiveCell.Offset(0, 1).Value = j
ActiveCell.Offset(0, 2).Value = k
'一行下に移動する
ActiveCell.Offset(1, 0).Select
End If
Next k
End If
Next j
Next i
End Sub
解答・その4
（ペンネ−ム：falcon@中学教師）
＜答え＞
６，１９，３０
（６＋１９＝２５、６＋３０＝３６、１９＋３０＝４９）
＜考え方＞
求める３数をa,b,cとおき、足して得られる平方数をx,y,zとする。
（a＜b＜c, x＜y＜z）
最小の平方数xを平方数の小さい方から固定する。
aとbの差が、yとzの差と同じであることを利用して、cを含めた3数のあたりをつけていく。
あとはその流れでしらみつぶしにやっていくことで見つけた。
解答・その5
（ペンネ−ム：オヤジ）
∴ ６，１９，３０ の組
∵ 求める異なる3数を
Ｘ ：一番小さな数
Ａ２−Ｘ ：２番目に小さな数
Ｂ２−Ｘ ：１番目に大きな数
とし（Ａ２−Ｘ）＋（Ｂ２−Ｘ）＝Ｃ２ と成ることから考える
但し Ａ＜Ｂ≦Ｃとする
解答・その6
（ペンネ−ム：のっこん）
３数をa,b,c（a＜b＜c）とする p+q=X, pq=Y とする
aを定めた時の、aとの和が平方数になる数を小さい順に並べる
（これは言わばb,c候補のリストである）
| a=1 の時 | ３ | ８ | １５ | ２４ | ３５ | ４８ | ６３ | ８０ | ９９ | この数列の一般項は n2+2n |
|---|---|---|---|---|---|---|---|---|---|---|
| a=2 の時 | ７ | １４ | ２３ | ３４ | ４７ | ６２ | ７９ | ９８ | この数列の一般項は n2+4n+2 | |
| a=3 の時 | ６ | １３ | ２２ | ３３ | ４６ | ６１ | ７８ | ９７ | この数列の一般項は n2+4n+1 | |
| a=4 の時 | ５ | １２ | ２１ | ３２ | ４５ | ６０ | ７７ | ９６ | この数列の一般項は n2+4n | |
| a=5 の時 | １１ | ２０ | ３１ | ４４ | ５９ | ７６ | ９５ | この数列の一般項は n2+6n+4 | ||
| a=6 の時 | １０ | １９ | ３０ | ４３ | ５８ | ７５ | ９４ | この数列の一般項は n2+6n+3 | ||
| a=7 の時 | ９ | １８ | ２９ | ４２ | ５７ | ７４ | ９３ | この数列の一般項は n2+6n+2 | ||
| a=8 の時 | １７ | ２８ | ４１ | ５６ | ７３ | ９２ | この数列の一般項は n2+8n+8 | |||
| a=9 の時 | １６ | ２７ | ４０ | ５５ | ７２ | ９１ | この数列の一般項は n2+8n+7 | |||
| a=10 の時 | １５ | ２６ | ３９ | ５４ | ７１ | ９０ | この数列の一般項は n2+8n+6 | |||
| a=11 の時 | １４ | ２５ | ３８ | ５３ | ７０ | ８９ | この数列の一般項は n2+8n+5 | |||
| a=12 の時 | １３ | ２４ | ３７ | ５２ | ６９ | ８８ | この数列の一般項は n2+8n+4 | |||
| a=13 の時 | ２３ | ３６ | ５１ | ６８ | ８７ | この数列の一般項は n2+10n+12 |
１）a=1の時の一般項はn2+2n だからb=p2+2p, c=q2+2q とおく
b+c=p2+q2+2p+2q=X2-2Y+2X
=（X+1）2-2Y-1
-2Y+2X=0 とするとX=Y （p-1）（q-1）=1 より p=q=2 がこれを満たすがp＜q に反するから不適
-2Y-1=0 とすると2Y=-1・・・不適
2) a=2の時の一般項はn2+4n+2 だからb=p2+4p+2, c=q2+4q+2 とおく
b+c=p2+q2+4p+4q+4=X2-2Y+4X+4
=（X+1）2-2Y-1+2X+4
=（X+2）2-2Y-4+4
-2Y+4X+4=0 とすると Y-2X=2 （p-2）（q-2）=6 より （p,q）=（3,8）、（4,5）がこれを満たす
p=3,q=8 の時、b=23,c=98 よってこの時、３数の和は１２３・・・・・※１
p=4,q=5 の時、b=34,c=47 〃 ８３・・・・・※２
-2Y-1+2X+4=0 とすると 2(Y-X）=3・・・不適
-2Y-4+4=0 とすると Y=0・・・不適
3) a=3の時の一般項はn2+4n+1 だからb=p2+4p+1,c=q2+4q+1 とおく
b+c=X2-2Y+4X+2
=（X+1）2-2Y-1+2X+2
=（X+2）2-2Y-4+2
-2Y+4X+2=0 とすると Y-2X=1 （p-2）（q-2）=5 より p=3,q=7 がこれを満たす
この時、b=22,c=78 となるから ３数の和は１０３・・・・・・※３
-2Y-1+2X+2=0 とすると 2（Y-X）=1・・・不適
-2Y-4+2=0 とすると Y=-1・・・・不適
4) a=4の時は同様にb+c=X2-2Y+4X
=（X+1）2-2Y-1+2X
=（X+2）2-2Y-4
-2Y+4X=0 とすると Y=2X （p-2）（q-2）=4 よりp=3,q=6 がこれを満たす
この時、b=21,c=60 となるから ３数の和は８５・・・・・・※４
-2Y-1+2X=0 とすると 2（X-Y）=1・・・不適
-2Y-4=0 とすると Y=-2・・・不適
5) a=5の時は同様にb+c=X2-2Y+6X+8
=（X+1）2-2Y-1+4X+8
=（X+2）2-2Y-4+2X+8
=（X+3）2-2Y-9+8
-2Y+6X+8=0 とすると Y=3X+4 （p-3）(q-3）=13 よりp=4,q=16 がこれを満たす
この時、b=44,c=356 となるから ３数の和は４０５・・・・・・※５
-2Y-1+4X+8=0 とすると 2（Y-2X）=7・・・不適
-2Y-4+2X+8=0 とすると Y=X+2 (p-1)(q-1)=3 よりp=2,q=4 がこれを満たす
この時、b=20,c=44 となるから ３数の和は６９・・・・・・※６
-2Y-9+8=0 とすると 2Y=-1・・・不適
6) a=6の時は同様にb+c=X2-2Y+6X+6
=(X+1)2-2Y-1+4X+6
=(X+2)2-2Y-4+2X+6
=(X+3)2-2Y-9+6
-2Y+6X+6=0 とすると Y=3X+3 (p-3)(q-3)=12 より
(p,q)=(4,15),(5,9),(6,7)がこれを満たす
p=4,q=15 の時、b=43,c=318 よってこの時、３数の和は３６７・・・・・・※７
p=5,q=9 の時、b=58,c=138 〃 ２０２・・・・・・※８
p=6,q=7 の時、b=75,c=94 〃 １７５・・・・・・※９
-2Y-1+4X+6=0 とすると 2(Y-2X)=5・・・不適
-2Y-4+2X+6=0 とすると Y=X+1 (p-1)(q-1)=2 よりp=2,q=3 がこれを満たす
この時、b=19,c=30 となるから ３数の和は５５・・・・・・※１０
-2Y-9+6=0 とすると 2Y=-3・・・不適
※１〜※１０により a=1〜6の時の和の最小値は５５であることがわかった
以降は５５以下の和があるかどうか調べる
7) a=7 の時
(a,b,c)=(7,9,18) は和は３４であるが、bとcの和は平方数でない
=(7,9,29) は和は４５であるが、 〃
=(7,18,29) は和は５４であるが、 〃
これ以外に和が５５以下となる組合せはない
8) a=8 の時
(a,b,c)=(8,17,28) は和は５３であるが、bとcの和は平方数でない
これ以外に和が５５以下となる組合せはない
9) a=9 の時
(a,b,c)=(9,16,27) は和は５２であるが、bとcの和は平方数でない
これ以外に和が５５以下となる組合せはない
10) a=10 の時
(a,b,c)=(10,15,26) は和は５１であるが、bとcの和は平方数でない
これ以外に和が５５以下となる組合せはない
11) a=11 の時
(a,b,c)=(11,14,25) は和は５０であるが、bとcの和は平方数でない
これ以外に和が５５以下となる組合せはない
12) a=12 の時
(a,b,c)=(12,13,24) は和は４９であるが、bとcの和は平方数でない
これ以外に和が５５以下となる組合せはない
13) a=13 の時
和が５５以下となる組合せはない
・・・・・・・・・・（以下同じ）・・・・・・・・・・・
従って和が最小となる３数の組は （６，１９，３０）
解答・その7
（ペンネ−ム：ykak）
答え ６，１９，３０
答えの３つの数字をa,b,cとし、これらのうちの２つを加えて出来る平方数をx,y,zとすると次の関係が成り立つ。
なお、a,b,cが相異なるから、x,y,zもそれぞれ異なる。
a + b = x
b + c = y (1)
c + a = z
これらをa,b,cの連立方程式と考えて解くと
a = x - y + z / 2
b = x + y - z / 2 (2)
c = -x + y + z / 2
となる。
x,y,zは平方数だから、小さいほうから順に４，９，１６，２５，３６，４９，６４となるが、
このうa,b,cの和が一番小さくなる物を見つければよい。
例えば、x = ４，y = ９，z = １６の組み合わせを考えると、bがマイナスになるので題意に合わない。
また(2)の各式の右辺は２で割って整数になるから分母は偶数でなければならない。
これらを使ってa,b,cの和が最小になる組を探すと、２５，３６，４９が該当する。これ
からa,b,cを計算すると６，１９，３０となる。
解答・その8
（ペンネ−ム：スモークマン）
やっとわかりました ^^;v...楽しめました♪
a＜b＜c とする...
a+b=x2
a+c=y2
c-b=y2-x2
b+c=z2
b=(z2-y2+x2)/2
c=(z2+y2-x2)/2
a=(x2+y2-z2)/2
偶―偶―偶、偶―奇―奇の組み合わせ
x＜y＜z …なので…
偶―偶―偶のとき…
(2m)2+(2m+2)2-(2m+4)2＞0 になるには…
(m+1)(m-3)>0…から…m≧4
つまり…8≦x
偶―奇―奇…
(2m)2+(2m+1)2-(2m+3)2＞0
m2-2m-8>0…m≧4…8≦x
奇―偶―奇…
(2m-1)2+(2m)2-(2m+2)2＞0…m≧4…7≦x
奇―奇―偶…
(2m-1)2+(2m+1)2-(2m+2)2>0…
2m2-4m-1＞0…m≧3…5≦x
よって…x=5 の場合を考える…
5-6-7 であればそれが最小になる…
a=(52+62-72)/2=6
b=(72-62+52)/2=19
c=(72+62-52)/2=30
じっさいに…
6+19=522、6+30=62、19+30=72で成立している♪
解答・その9
（ペンネ−ム：MVH）
まず, 組（６，１９，３０）は, どのつの和も平方数になる.
以下では, この組の３数の和が最小であることを示し, 求める答えであることを示す.
求める組を（ａ，ｂ，ｃ）とおく. 但し,１≦ａ＜ｂ＜ｃ である, とする.
ここで, ａ＋ｂ＝ｋ２、ａ＋ｃ＝ｌ２、ｂ＋ｃ＝ｍ２より,
ａ，ｂ，ｃをｋ、ｌ、ｍを用いて表すと,
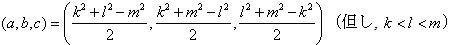
を得る. これより, 組（ｋ，ｌ，ｍ）が決まれば, 組（ａ，ｂ，ｃ）は決まるから,
組（ｋ，ｌ，ｍ）を考えれば良く,
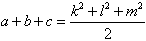より, ｋ２＋ｌ２＋ｍ２ が最小になる組（ｋ，ｌ，ｍ）を求めれば良い.
組（６，１９，３０）において, ｋ２＋ｌ２＋ｍ２＝１１０ だから, これより, 小さい組（ｋ，ｌ，ｍ）が存在すると仮定して, ｋ２＋ｌ２＋ｍ２＜１１０（・・・(1)）としてよい.
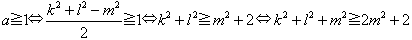
これと(1)とより,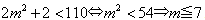 
一方,
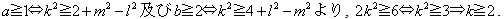
さて, 奇数を「き」, 偶数を「ぐ」と表すことにすると,
組（ｋ，ｌ，ｍ）は, 「き, き, ぐ（の並べ替え）」または「ぐ, ぐ, ぐ」のいずれかであることが必要（それ以外の場合では, 自然数が存在しない）.
以上により, 組（ｋ，ｌ，ｍ）の候補は, 以下の９通りに絞られる.
（ｋ，ｌ，ｍ）＝（４，５，７）、（２，５，７）、（３，６，７）、（３，４，７）、（２，３，７）、（３，５，６）、（３，４，５）、（２，３，５）、（２，４，６）.
しかし, いずれの場合も,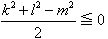 
となり, 不適.
よって, 求める組は, （６，１９，３０）.
解答・その10
（ペンネ−ム：転位反応）
３つの正整数を Ａ＞Ｂ＞Ｃ＞０ とし、
それらの２数の和である平方数をＬ２、Ｍ２、Ｎ２とする。
Ａ＋Ｂ＝Ｌ２
Ａ＋Ｃ＝Ｍ２
Ｂ＋Ｃ＝Ｎ２
ここで、Ｌ２＞Ｍ２＞Ｎ２
Ａ、Ｂ、Cについて解くと、
Ａ＝１／２（Ｌ２＋Ｍ２−Ｎ２） ・・・(1)
Ｂ＝１／２（Ｌ２−Ｍ２＋Ｎ２） ・・・(2)
Ｃ＝１／２（−Ｌ２＋Ｍ２＋Ｎ２） ・・・(3)
ここで、Ａ、Ｂ、Ｃは正整数であるから、右辺の括弧内は偶数である。
よって、Ｌ２、Ｍ２、Ｎ２は全て偶数、又は、２つが奇数で１つは偶数である。
（１）Ｌ２、Ｍ２、Ｎ２ が全て偶数のケース
偶数の平方数を列挙し、小さい方から順に上記(1)(2)(3)を満たす平方数の組合せを検証すると、６４、１００、１４４ となる。
４、１６、３６、６４、１００、１４４、１９６、・・・・・
よって、Ａ＝９０、Ｂ＝５４、Ｃ＝１０
（２）Ｌ２、Ｍ２、Ｎ２の２つが偶数で、１つは奇数のケース
平方数を列挙し、小さい方から順に上記(1)(2)(3)を満たす満たす平方数の組合せを検証すると、２５、３６、４９ となる。
１、４、９、１６、２５、３６、４９、６４、８１、１００、１２１、・・・・・
よって、Ａ＝３０、Ｂ＝１９、Ｃ＝６
以上より、題意を満たす正整数は、６、１９、３０ である。
解答・その11
（ペンネ−ム：バルタン星人）
答え：６，１９，３０
考え方：３数をａ，ｂ，ｃ（ａ＜ｂ＜ｃ）とする。
ａ＋ｂ＝ｘ ａ＋ｃ＝ｙ ｂ＋ｃ＝ｚとする。
ａ，ｂ，ｃが奇数０−３個の何れの場合でも、ｘ、ｙ、ｚの何れかは必ず偶数になる。
偶数の平方数は、４，１６，３６、６４・・・・・。
１）４の場合
ａ＝１ ｂ＝３となるが題意を満たすｃはない。
２）１６の場合
ｘ＝１６なら ｙ＝２５、ｚ＝４９（ｚ−ｙ＝ｂ−ａは偶数でなければならない）となり解はない。
ｙ＝１６の場合（０，９，１６）が解となるが正の整数の条件に反する。
Ｚ＝１６も解なし。
３）３６の場合
ｘ＝３６なら ｙ＝４９ ｚ＝８１となり（２，３４，４７）が解
ｙ＝３６なら ｘ＝２５ ｚ＝４９となり（６，１９，３０）が解
ｚ＝３６ 解なし
（６，１９，３０）の和は５５なので６４は検討の必要なし。
解答・その12
（ペンネ−ム：巷の夢）
相異なる3個の正整数をＡ，Ｂ，Ｃ（Ａ＜Ｂ＜Ｃ）とすると、題意より
Ａ＋Ｂ ＝ｘ２ ・・・・・(1)
Ａ＋ Ｃ＝ｙ２ ・・・・・(2)
Ｂ＋Ｃ＝ｚ２ ・・・・・(3)
が成立する。
ところで、Ａ＜Ｂ＜Ｃ ・・・・・(4) より ｘ＜ｙ＜ｚ ・・・・(5)である。
また、(1)〜(3)より 2（Ａ＋Ｂ＋Ｃ）＝ｘ２ ＋ｙ２ ＋ｚ２ であり、
ｘ２ ＋ｙ２ ＋ｚ２は偶数でなければならない。
3数の合計が偶数になるのは偶 ＋偶 ＋偶 ないし奇 ＋奇 ＋偶の場合のみである。
１）3数が全て偶数の場合
平方数が偶数であるのは、4,16,36,64,100,144・・・・・・・であり、
(1)〜(3)より ｚ２ ＜ｘ２ ＋ｙ２ である。
これに合う相異なる3個の正整数の和が最小になる組み合わせは64,100,144となる。
因って、これよりＡ，Ｂ，Ｃの値を求めると、
各々Ａ＝10 Ｂ＝54 Ｃ＝90となる。
２）2数が奇数で１数が偶数の場合
一番大きな数が奇数の場合の最小組み合わせは25,36,49となる。
因って、これよりＡ，Ｂ，Ｃの値を求めると、
各々Ａ＝6 Ｂ＝19 Ｃ＝30となる。
尚、一番大きな数が偶数の場合の最小組み合わせは25,49,64となる。
因って、これよりＡ，Ｂ，Ｃの値を求めると、各々Ａ＝5 Ｂ＝20 Ｃ＝44となる。
以上の3つの組み合わせを比較し、求める数は6,19,30となる。
解答・その13
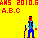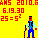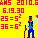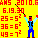（ペンネ−ム：杖のおじさん）
答え
（A,B,C）→ （６、１９，３０）です。
A+B=X2⇒A=X2―B・・・(1)
A+C=Y2⇒A=Y2―C・・・(2)
B+C=Z2・・・・・・・・(3)
(3)を(4)に代入する
２A=X2+Y2―（B＋C）→
A=（X2+Y2―Z2）/2・・・(5)
A,B,Cは整数なのでX2、Y2、Z2は全部偶数か奇数が２個ある事になります。
この条件が満すことの出来る数字を次の数列（X2）から調べます。
１、４．９．１６ ２５，３６，４９、６４
(5)の式を使って順番にAを求めます。
１．４．９ の場合 A= −２．５ 整数でないのでだめです。
４，９，１６の場合 A= −１．５ 整数でないのでだめです。
９、１６、２５の場合 A= ０ 整数なのでBを調べる
B=９＋２５−３４＝０でありA＜Bの条件に合わないのでだめです。
１６、２５，３６、の場合 A=２．５ 整数でないのでだめです。
２５、３６、４９の場合
A=（２５＋３６−４９）/２＝６なので（整数です。）
B=X2−A・・・(6) B=Z2―C・・・(7) A+C=Y2・・・(8)
(7)＋(8)＝２B=X2+Z2−（A+C）→ B= （X2+Z2−（A+C））/２
B=（２５＋４９−３６）/2＝１９なので（整数です）
C=Z2−B・・・(9) C=Y2−A・・・(10) A+B=X2・・・(11)
(9)＋(10) = ２C=Z22+Y2−（A+B)→
C= （Z2+Y2−（A+B)）/２＝３０なので整数です。
従って A=６ B=１９ C=３０ になります。
解答・その14
（ペンネ−ム：T_Tatekawa）
3つの正整数を a, b, c と置きます．
次に整数 p, q, r を
a + b = p2
b + c = q2
c + a = r2
となるようにします．これらを a, b, c について解くと，
a = (r2 + p2 - q2)/2
b = (p2 + q2 - r2)/2
c = (q2 + r2 - p2)/2
となります．ここから，a, b, c が正であるためには，
p2 + q22＞r2, q2 + r2＞p2,
r2 + p2＞q2
という条件がつきます．
一辺の長さが p, q, r の三角形を考えると，この三角形は
鋭角三角形になります．以下，「鋭角三角形の条件」と呼ぶ事に
します．
また，a, b, c が正整数なので，
i) p, q, r のうち2つが奇数で1つが偶数
ii) p, q, r の全てが偶数
のいずれかでなければなりません．
i) の場合，なるべく数字を小さくするため p, q, r を 1 刻みでずらします．
(1, 2, 3) では鋭角三角形の条件を満たしません．
(3, 4, 5) では直角三角形になります．
(5, 6, 7) の場合は
a+b=25, b+c=36, c+a=49
なので
a=19, b=6, c =30
となります．このとき a+b+c=55 です．
ii) の場合，今度は p, q, r を2刻みでずらします．
(2, 4, 6) では三角形が線分に潰れます．
(4, 6, 8) では鋭角三角形の条件を満たしません．
(6, 8, 10) では直角三角形になります．（(3, 4, 5) の2倍の長さ）
(8, 10, 12) の場合は鋭角三角形の条件を満たします．この時は
a+b=64, b+c=100, c+a=144
なので，
a=54, b=10, c=90
となり，a+b+c=154 です．
i) の方が a+b+c が小さいです．
答えは 55 です．
解答・その15
（ペンネ−ム：ＲＹＵ1128）
仮定
1 a,b,cは正の整数でa≠b≠c
2 P,Q,Rは平方数
3 a+b=P
b+c=Q
c+a=R ・・・(1)
a+b+c=(P+Q+R)/2 ・・・(2)
a=( P-Q+R)/2 P+R＞Q
b=( P+Q-R)/2 P+Q＞R
c=(-P+Q+R)/2 ・・・(3)
Q+R＞P ・・・(4)
(5) (2)よりP,Q,Rは全数偶数か2数が奇数
(6) (4)よりP,Q,Rは何れも他の2数の和より小さい
(7) (3)よりP=Qとするとa=cとなり仮定1に反するからP≠Q≠R
(8) 今P＜Q＜R ,p=√P, q=√Q, r=√R 仮定1,3よりP＞3
p=2 P=4の場合 r=q+1とすると R=(q+1)2=q2+2q+1=Q+2q+1
q＞2よりR-Q＞4 (6)より成立しない
p=3 P=9の場合 r=q+1とすると R=(q+1)2=q2+2q+1=Q+2q+1
q＞3よりR-Q≧9 (6)より成立しない
p=4 P=16の場合 r=q+1とすると R=(q+1)2=q2+2q+1=Q+2q+1
q＞4よりR-Q＞11
そこでQ=25とすると(5)よりR≧49なる奇平方数で無ければ成立しない
またQ=36とすると(5)よりR≧64なる遇平方数で無ければ成立しない
よって成立しない
p=5 P=25の場合 r=q+1とすると R=(q+1)2=q2+2q+1=Q+2q+1
q＞5よりR-Q＞13
そこでQ=36とすると(5)よりR≧49なる奇平方数R=49はR-Q＜Pとなり(6)を満たす
仮定をすべて満たすことから
(3)よりa=19,b=6,c=30・・・・・・・・(9)
また(2)より平方数の和(P+Q+R)が最小であれば求める数の和a+b+cは最小
(8)よりPが成立する最小数でありP,Q,Rは連続した平方数であること
以上より(9)の組み合わせが最小であると結論できる。
解答・その16
（ペンネ−ム：teki）
＜答え＞ ６、１９、３０ （合計 ５５）
３数をa,b,cとすると、
２×（a+b+c）＝p2+q2+r2
が成立します。（p,q,rは異なる自然数）
あとは、p,q,rに小さい順に数値を当てはめました。
（ただし、p,q,rは３つとも偶数、または２つが奇数で１つが偶数）
小さい順に当てはめると、p=5,q=6,r=7 のとき、上記の解が見つかります。
蛇足ですが、これ以外にも解は多数あります。
一例を挙げると、p=5,q=7,r=8 のとき、a=5,b=20,c=44 といった解もあります。
この問題、a,b,cを当てはめるアプローチだと、これが最小解のように思われますが、違いますね。
あまりスマートな解法ではないですが、他にうまい方法が見つかりませんでした。
解答・その17
（ペンネ−ム：迷子の雄猫）
相異なる３つの正整数を小さい順にa,b,c、
a+bをX、a+cをY、b+cをZとおく。
YとZの差はaとbの差であるので、bよりも小さい。（条件１）
XとZの差はaとcの差であるので、cよりも小さい。（条件２）
また、X+Y+Z=a+b+a+c+b+c=2a+2b+2c=2(a+b+c)となるので、
X,Y,Zは全て偶数であるか、奇数２個と偶数１個である。（条件３）
平方数を小さいほうからあげると、1,4,9である。
X,Y,Zを順に1,4,9と仮定すると、（条件１）よりbは5よりも大きい。
よってXは9以上。
X,Y,Zを順に9,16,25と仮定すると、（条件１）よりbは9よりも大きい。
よってXは16以上。
X,Y,Zを順に16,25,36と仮定すると、（条件３）を満たさないが、
（条件１）よりbは11よりも大きい。
（条件２）よりcは20よりも大きい。
X,Y,Zを順に25,36,49と仮定すると、（条件１）よりbは13よりも大きい。
（条件２）よりcは24よりも大きい。
a,b,cを6,19,30とすると、a+b=25、a+c=36、b+c=49となるので題意を満たす。
このときの３数の和は55。
X,Y,Zを順に16,36,64と仮定すると、（条件３）を満たすが、
３数の和が58となるので、３数の和が最小になる組合せではない。
よって、求める相異なる３つの正整数の組は、6,19,30
解答・その18
（ペンネ−ム：夜ふかしのつらいおじさん）
求める数を、ａ，ｂ，ｃ とします。
平方数をｓkとすると、
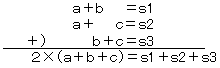
∴ ３個の平方数の和は偶数なので、平方数のうち奇数であるものは、偶数個です。
ａ＋ｂ＋ｃ＝１／２×（ｓ1＋ｓ2＋ｓ3）＝Ｓとおきます。
ａ＝Ｓ−（ｂ＋ｃ）＝１／２×（ｓ1＋ｓ2＋ｓ3）−ｓ3＝１／２×（ ｓ1＋ｓ2−ｓ3）＞０
ｂ＝Ｓ−（ａ＋ｃ）＝１／２×（ｓ1＋ｓ2＋ｓ3）−ｓ2＝１／２×（ ｓ1−ｓ2＋ｓ3）＞０
ｃ＝Ｓ−（ａ＋ｂ）＝１／２×（ｓ1＋ｓ2＋ｓ3）−ｓ1＝１／２×（−ｓ1＋ｓ2＋ｓ3）＞０
まとめると ｓi＋ｓj＞ｓk （ または、ｓi＞ｓk−sj ）
つまり、２つの和は残りの１つより大きい。 （ または、２つの差は残りの１つより小さい）
∴ ３個の平方数で三角形を作ることができます。
以上から平方数について、小さい方から２数の和が他の数より大きい組みを探していくと、
（１）３個とも偶数のとき、
偶数の平方数は、{4, 16, 36, 64, 100, 144, 196, 256, 324, 400, ・・・} などです。
（２）２個が奇数、１個が偶数のとき
奇数の平方数は、{1, 9 , 25, 49, 81, 121, 169, 225, 289, 361, ・・・} などです。
偶数の平方数は、{4, 16, 36, 64, 100, 144, 196, 256, 324, 400, ・・・} などです。
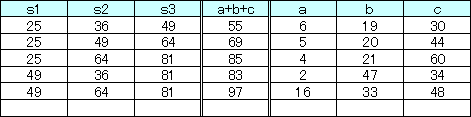
以上から、最小の組合せは、{6, 19, 30} です。
解答・その19
（ペンネ−ム：遊名人）
求める3つの整数をa,b,cとする。
0＜a＜b＜c としても一般性を失わない。ここでp,q,rを自然数として
a + b = p2 (1)
b + c = q2 (2)
c + a = r2 (3)
と書ける。このとき大小関係よりp＜r＜q, また明らかにp≧2である。
(1)+(2)+(3)より
a + b + c = (p2 + q2 +r2)/2 だから
a = (p2 - q22 + r2)/2 (4)
b = (p2 + q2 - r2)/2 (5)
c = (-p2 + q2 + r2)/2 (6)
と求まる。
p=2のとき
条件をみたすq,rは存在しない。
なぜならa≧1かつq≠rとなるためには(4)よりq2-r2=2でないといけないが、
q2-r2=(q+r)(q-r)=2とするとq+r=2, q-r=1で不適だからである。
p=3のとき
(4)から q2-r2=(q+r)(q-r) = 7,5,3,1のいずれかである。
q2-r2=1とすると q+r=1, q-r=1・・・不適
q2-r2=3とすると q+r=3, q-r=1・・・q=2,r=1でpが最小に反する。
q2-r2=5とすると q+r=5, q-r=1 ・・・q=3,r=2 不適
q2-r2=7とすると q+r=7, q-r=1 ・・・q=4,r=3 これも不適
p=4のとき
q+rとq-rは偶奇が一致するので、q2-r2を4で割った余りが2になることはない
ことに着目すると、(4)よりq^2-r^2=12,8,4のいずれか。
q2-r2=4 →q+r=2, q-r=2 不適
q2-r2=8 →q+r=4, q-r=2 →q=3,r=1 不適
q2-r2=12 →q+r=6, q-r=2 →q=4, r=2 不適
p=5のとき
(4)からq2-r2=23,21,19,17,15,13,11,9,7,5,3,1の可能性がある。
q2-r2=7,5,3,1は不適であることは先にp=3の場合で示した。
q2-r2=9 →q+r=9, q-r=1 →q=5, r=4 不適
q2-r2=11 →q+r=11, q-r=1 →q=6, r=5 不適
q2-r2=13 →q+r=13, q-r=1 →q=7, r=6 OK
q2-r2=15, 17, 19, 21, 23は条件をみたす最小解とならない。
よって、p=5,q=7, r=6すなわち a=6, b=19, c=30が最小解である。
答え：3数は(6,19,30)、和は55
解答・その20
（ペンネ−ム：三角定規）
【解答】
３つの正整数を ａ，ｂ，ｃ とすると，題意より ｌ，ｍ，ｎ （ｌ＜ｍ＜ｎ） を整数として
ａ＋ｂ＝ｌ2 ……(1)
ｂ＋ｃ＝ｍ2 ……(2)
ｃ＋ａ＝ｎ2 ……(3)
ａ＋ｂ＋ｃ＝(ｌ2＋ｍ2＋ｎ2)/2 ……(4)
(4)−(2)： ａ＝(ｌ2−ｍ2＋ｎ2)/2 ……(5)
(4)−(3)： ｂ＝(ｌ2＋ｍ2−ｎ2)/2 ……(6)
(4)−(1)： ｃ＝(−ｌ2＋ｍ2＋ｎ2)/2 …(7)
(5)(6)(7)より，ａ，ｂ，ｃ が整数になるためには，ｌ，ｍ，ｎ はすべて偶数，または １つが偶数２つが奇数でなければならず，ａ＋ｂ＋ｃ を最小にするには(4)よ り，ｌ，ｍ，ｎ は連続した３整数であることが必要である。
以上より，ａ＋ｂ＋ｃ を最小にするのは，(ｌ，ｍ，ｎ)＝(5，6，7) のときの (a，b，ｃ)＝(19，6，30)
正解者
| 浜田 明巳 | 迷子の雄猫 | スモークマン |
| teki | ＲＹＵ1128 | 夜ふかしのつらいおじさん |
| 巷の夢 | 転位反応 | のっこん |
| 遊名人 | エルドス | オヤジ |
| 杖のおじさん | T_Tatekawa | falcon@中学教師 |
| haya | ykak | 三角定規 |
| MVH | バルタン星人 |
コメント
求める３つの正整数をa,b,cとすると、整数l,m,nを用いて、
ａ＋ｂ＝ｌ2
ｂ＋ｃ＝ｍ2
ｃ＋ａ＝ｎ2
と書くことができます。辺々を足すと、
２（ａ＋ｂ＋ｃ）＝ｌ2＋ｍ2＋ｎ2
より、右辺は偶数ですから、l,m,n の偶数・奇数の絞りこみができます。
さらに、三角定規さんの解答にあるように、
a+b+cを最小にするためには、l,m,n は連続した３整数であるということが、
ポイントですね。
top