Challenge!

問題160　色の塗り方
Weekend Mathematics／問題／問題160　色の塗り方

問題160　色の塗り方

一列に並んだ６個のマスを赤、白、黒のいずれかの色で塗り分ける。 ただし、赤いマスが連続してはいけないものとする。 塗り分け方は何通りあるか。

問題の出典

ジュニア数学オリンピック2003-2008
数学オリンピック財団編
日本評論社

答えと解説

解答・その1

（ペンネ－ム：浜田　明巳）

ＥＸＣＥＬのマクロで解きました．答は４４８通りです．
赤，白，黒をそれぞれを１，２，３で表し，各マスに入る数を最初からａ(ｎ)（１≦ｎ≦６）とする．
ｎ＝１のとき，１≦ａ(１)≦３
２≦ｎ≦６のとき，
　　ａ(ｎ－１)＝１のとき２≦ａ(ｎ)≦３，
　　ａ(ｎ－１)≧２のとき１≦ａ(ｎ)≦３となる．
これを元にマクロを使って，ａ(１)からａ(６)を求める．

Option Explicit
Dim a(6) As Integer
Sub Macro1()
    Sheets("Sheet1").Select
    Cells(1, 1).Value = 0 '答
    Call saiki(1)
    Range("A1").Select
End Sub
Sub saiki(ByVal n As Integer)
    Dim j As Integer
    If n = 1 Then
      a(1) = 1
    ElseIf a(n - 1) = 1 Then '赤は連続しない
      a(n) = 2
    Else
      a(n) = 1
    End If
    While a(n) <= 3
      If n < 6 Then
        Call saiki(n + 1)
      Else
        Cells(1, 1).Value = Cells(1, 1).Value + 1
        For j = 1 To 6
          Cells(Cells(1, 1).Value, j + 1).Value = masu(a(j))
        Next j
        Range("B" & Cells(1, 1).Value).Select
      End If
      a(n) = a(n) + 1
    Wend
End Sub
Private Function masu(ByVal n As Integer) As String
    Select Case n
      Case 1
        masu = "赤"
      Case 2
        masu = "白"
      Case Else
        masu = "黒"
    End Select
End Function


解答・その2

（ペンネ－ム：巷の夢）

問題の条件を考慮し、組み合わせを考えると下記の表のように整理され、 赤は続きの桝に入れない、即ち、赤が2個の場合6C2＝15でなく10通り、 赤が3個の場合は6C3＝20でなく4通りであることに注意すれば良い。

色数黒白赤組み合わせ
16001
0601
25106
5016
1506
0516
42015
40210
24015
04210
33020
3034
0334
341130
14130
32160
31240
23160
13240
21312
12312
22260
合計448
即ち、求める個数は448通りである。

解答・その3

（ペンネ－ム：のっこん）

白、黒については隣り合ったマス同士が同色でもよいと解釈しました
６個のマスをA,B,C,D,E,Fとする
前半の３つのマスA,B,Cについて考える
　Aが赤でCが赤・・・２通り
　Aが赤でCが白・・・２通り
　Aが赤でCが黒・・・２通り
　Aが白でCが赤・・・２通り
　Aが白でCが白・・・３通り
　Aが白でCが黒・・・３通り
　Aが黒でCが赤・・・２通り
　Aが黒でCが白・・・３通り
　Aが黒でCが黒・・・３通り
まとめると
　Aが赤・・・６通り、Aが白・・・８通り、Aが黒・・・８通り
　Cが赤・・・６通り、Cが白・・・８通り、Cが黒・・・８通り
後半の３つのマスD,E,Fについても同様だからAをDと読みかえて
　Dが赤・・・６通り、Dが白・・・８通り、Dが黒・・・８通り
１）Cが赤となる６通りについては、Dが白か黒の１６通りとつなげてよい
２）Cが白となる８通りについては、Dは何色でもよいので２２通りとつなげてよい
３）Cが黒となる８通りについても、Dは何色でもよいので２２通りとつなげてよい
　６・１６＋８・２２＋８・２２＝４４８（通り）

解答・その4

（ペンネ－ム：ykak）

答え　４４８通り

考え方
３色使って６マスを塗る塗り方の数は全部で３の６乗＝７２９通りあるが、この中で赤が連続している塗り方 を数えてその数を全体の数から引く。
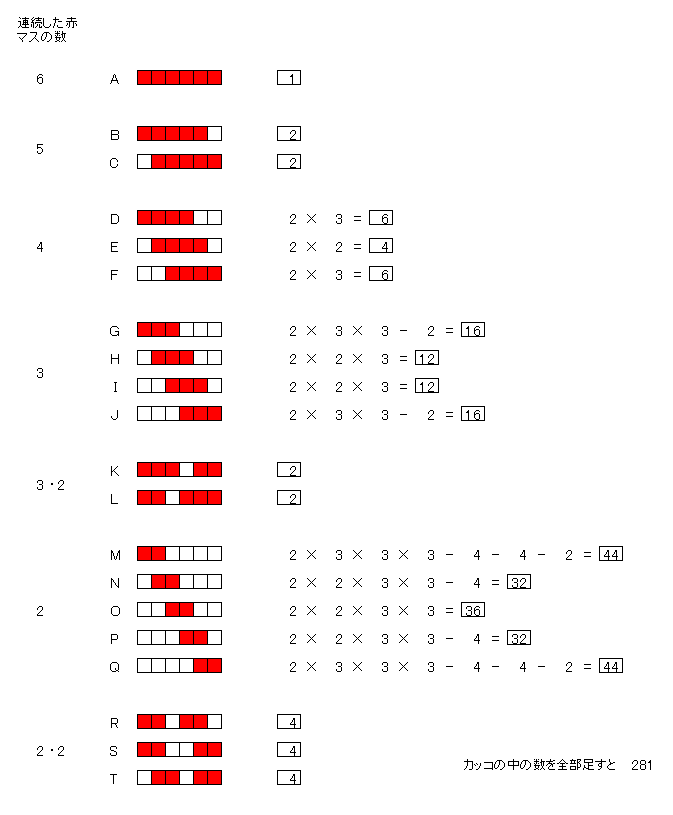
赤が連続している塗り方のパターンは、図のとおり全部で２０通りあり、これを順番にＡからＴとする。

  1. Ａは、赤が６マス連続している塗り方で、その塗り方は１通り　（Ａ＝１）

  2. Ｂ、Ｃは赤が５マス連続している塗り方で、赤でないマスは白か黒しか塗れないから、 その塗り方の数は、Ｂ、Ｃとも２通り。
    　　　（Ｂ、Ｃ＝２）

    　　　
  3. Ｄ、Ｅ、Ｆは赤が４マス連続している塗り方で、赤に隣接しているマスは白か黒、 それ以外ののマスは赤、白、黒とも塗れるから、その塗り方は、
    　　　ＤとＦが、２×３の６通り。　（Ｄ、Ｆ＝６）
    　　　Ｅは、２×２の４通り。　（Ｅ＝４）　

  4. ＧからＪは赤が３マス連続している塗り方であるが、その塗り方の数は次のとおり。
    1）　ＧとＪは赤のマスに隣接しているマスは白と黒の２通り、それ以外のマスは３通りだから、
    　　　２×３×３の１８通り。
    ただしＧの中にはＫの塗り方も含まれているが、これはＫのところで数えるのでその塗り方の数 （後で述べるとおり２通り）を除いて、Ｇは１６通りとする。
    ＪもＬの塗り方を含んでいるので、同様に１６通りとする。　（Ｇ、Ｊ＝１６）
    2）　ＨとＩは、赤のマスに隣接しているマスが２つあり、これは白と黒の２通りで、残りのマスが３通りだから
    　　　２×２×３の１２通り。　（Ｈ、Ｉ＝１２）

  5. ＫとＬは、赤マスが２個及び３個連続している塗り方で、残った１つのマスは白か黒しか塗れないから、 それぞれ２通り。　（Ｋ、Ｌ＝２）

  6. ＭからＱは赤マスが２個連続している塗り方であるが、その塗り方の数は次のとおり。
    1）　ＭとＱは、赤マスに隣接するマスの塗り方が白と黒の２通り、それ以外のマスが３通りだから、それぞれ 　　　２×３×３×３の５４通り。
    ただしＭの中には、Ｌ、Ｒ、Ｓの塗り方も含まれているが、それはそれぞれの場所で数えるので除外する。
    Ｌは上に述べた２通りで、ＲとＳは後で述べるように各４通りだから、
    　　　５４－２－４－４の４４通り。　（Ｍ＝４４）
    Ｑも同様に、Ｋ、Ｓ、Ｔの塗り方を含んでいるから４４通り。　（Ｑ＝４４）
    2）　Ｎ、Ｏ、Ｐは赤マスに隣接する２つのマスは２通り、それ以外の２つのマスは３通りだから
    　　　２×２×３×３の３６通り
    ただしＮはＴを含んでおり、ＰはＲを含んでいるから、それを除く。
    　　　３６－４の３２通り　（Ｎ、Ｐ＝３２）
    Ｏは重複するものがないのでそのまま３６通り　（Ｏ＝３６）

  7. Ｒ、Ｓ、Ｔは、空いている２つのマスは白か黒しか塗れないから
    　　　２×２の４通り　　（Ｒ、Ｓ、Ｔ＝４）

  8. 以上のＡからＴまでの塗り方の数を全部加えると２８１になる。

答えは、７２９－２８１＝４４８



解答・その5

（ペンネ－ム：長崎島原かがみ）

塗り方の総数は３の６乗だから７２９通り。
このうち，赤が２コマ以上連続している場合を除けばよい。


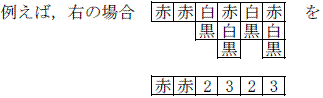
と書くことにし，場合の数は2×3×2×3＝36（通り）である。
では，パターンに分けて場合の数を求めることにする。


したがって，
７２９－２４１＝４８８（通り）
（答）４８８通り

解答・その6

（ペンネ－ム：スモークマン）

赤0：26=64
赤1：25*6C1=32*6=192
赤2：24*5C2=16*10=160
赤3：23*4C3=8*4=32
赤4：この場合必ず赤は連続しちゃう...赤の隙間は3個しかないので...残り2枚じゃ 無理だから...
けっきょく...
64+192+160+32=96+352=448 通り♪

解答・その7

（ペンネ－ム：falcon@中学教師）

４４８通り

＜考え方＞赤い色で塗り分けたマスの数で場合分けして考える。
（１） 赤いマスが６個、５個、４個の場合
これらの場合は、どのように配置しても赤いマスが連続するところが出てくるので、０通り。

（２） 赤いマスが３個の場合
赤いマスが連続しないような赤いマスの配置は
　・ 赤、□、赤、□、赤、□
　・ 赤、□、赤、□、□、赤
　・ 赤、□、□、赤、□、赤
　・ □、赤、□、赤、□、赤
の、４通り。
残りのマスは白か黒で塗り分けるので ２３ ＝８通り。
従って、この場合は４×８＝３２通りある。

（３） 赤いマスが２個の場合
赤いマスが連続しないような赤いマスの配置は
　・ 赤、□、赤、□、□、□
　・ 赤、□、□、赤、□、□
　・ 赤、□、□、□、赤、□
　・ 赤、□、□、□、□、赤
　・ □、赤、□、赤、□、□
　・ □、赤、□、□、赤、□
　・ □、赤、□、□、□、赤
　・ □、□、赤、□、赤、□
　・ □、□、赤、□、□、赤
　・ □、□、□、赤、□、赤
の、１０通り。
残りのマスは白か黒で塗り分けるので ２４ ＝１６通り。
従って、この場合は１０×１６＝１６０通りある。

（４） 赤いマスが１個の場合
赤いマスが連続することはありえない。赤いマスの配置は６通り。
残りのマスは白か黒で塗り分けるので ２５ ＝３２通り。
従って、この場合は６×３２＝１９２通りある。

（５） 赤いマスが０個の場合
赤いマスが連続することはありえない。
６個のマス全てを白か黒で塗り分けるので、この場合は ２６ ＝６４通りある。

（１）～（５）より、求める塗り分け方は０＋３２＋１６０＋１９２＋６４＝４４８通り。

解答・その8

（ペンネ－ム：オヤジ）

６個のマスに左から　１～６と番号を付ける。
例えば、赤を１番目、３番目、６番目に塗るのを　１－３－６ の様に表す。
赤を塗る個数によって場合分けする。

（Ⅰ)　赤マス　０個　の場合　　　白・黒のみ　・・２６　通り　＝　６４通り
（Ⅱ）赤マス　１個　の場合　　　６×２５　通り　＝　１９２通り
（Ⅲ）赤マス　２個　の場合　　
　　（１）１－３　　２４　通り
　　（２）１－４　　２４　通り
　　（３）１－５　　２４　通り
　　（４）１－６　　２４　通り
　　（５）２－４　　２４　通り
　　（６）２－５　　２４　通り
　　（７）２－６　　２４　通り
　　（８）３－５　　２４　通り
　　（９）３－６　　２４　通り
　　（10）４－６　　２４　通り
　（１）～（10）より　１０×２４　通り　＝　１６０　通り
（Ⅳ）赤マス　３個　の場合
　（１）１－３－５　　２３　通り　
　（２）１－３－６　　２３　通り
　（３）１－４－６　　２３　通り
　（４）２－４－６　　２３　通り
　（１）～（４）より　４×２３　通り　＝　３２　通り

（Ⅰ) ～（Ⅳ）は、排反事象より和の法則から
　　　６４＋１９２＋１６０＋３２＝　４４８　通り
　∴　４４８　通り

解答・その9

（ペンネ－ム：迷子の雄猫）

それぞれのマスは一色で塗り分けるとする。
赤いマスが連続してはいけないので、赤いマスの数は０マス以上３マス以下である。

赤いマスが０マスのとき：1通りのうち連続しないのは1通り
赤いマスが１マスのとき：6通りのうち連続しないのは6通り
赤いマスが２マスのとき：15通りのうち連続しないのは10通り
赤いマスが３マスのとき：20通りのうち連続しないのは4通り

さて、赤いマス以外はどのように塗ろうが構わないので、
赤以外のマスの数をxと置くと
（赤以外のマス目の塗り分け方）は２x通り
よって
　1×64　＋　6×32　＋　10×16　＋　4×8
＝　64　＋　192　＋　160　＋　32
＝　448
答え：448通り

解答・その10

（ペンネ－ム：T_Tatekawa）

赤のマスとそれ以外で区別します．

  1. 赤を使わない場合
    6個のマスを白，黒のいずれかで塗り分けるので，26 = 64 通り

  2. 赤を1つ使う場合
    白と黒で5つのマスを塗り分けで，その後で赤のマスを割り込ませる事を考える．
    白と黒の塗り分け方は 25=32 通り
    割り込ませる位置は 6 通り
    よって 32 x 6 = 192 通り

  3. 赤を2つ使う場合
    白と黒で4つのマスを塗り分けで，その後で赤のマスを別々の場所に割り込ませる事を考える．
    白と黒の塗り分け方は 24=16 通り
    割り込ませる位置は 5x4/2 = 10 通り
    よって 16 x 10 = 160 通り

  4. 赤を3つ使う場合
    ◯を白か黒，■を赤とすると，
    ◯■◯■◯■
    ■◯■◯■◯
    ■◯■◯◯■
    ■◯◯■◯■
    のいずれかの塗り方になる．
    白と黒の塗り分け方は 23=8 通り
    赤の入り方のパターンは 4通り
    よって 8 x 4 = 32

以上 1～4 を合計すると，
64 + 192 + 160 + 32 = 448通り

解答・その11

（ペンネ－ム：バルタン星人）

答え
４４８通り

考え方：以下の仮定のもとに解きました。
赤は連続しないとだけ書いてあるので白及び黒は連続して良い。
ますには一定の向きがあり、１８０度回転して同じ色の順番になっても それは別の塗り方とカウントする。

赤が０～３個で場合分けして考える。（4個以上は連続が出る）
　１）０個の場合は、２６＝２×２５
　２）１個の場合は６×２５
　３）２個の場合赤の塗り方が１０通り　１０×２４＝５×２５
　４）３個の場合、ますに１－６の順番をつけると赤の塗り方は
　　　（１，３，５）（１，３，６）（１，４，６）（２，４，６）
の４通りだから４×２３＝２５
これを足すと１４×２５＝７×６４＝４４８

解答・その12

（ペンネ－ム：シュレーディンガーの三毛猫）

＜答＞　448通り

＜解法＞
塗り分けられた６つのマスのうち赤いマスの数について場合分けし、条件を満たす場合の数を調べる。

（１．　一般に、ｎ個の要素からｒ個を選ぶ場合の数(組み合わせ)は以下の式で表せる。
　　　ｎＣｒ≡ｎ！/ｒ！（ｎ - ｒ）！
　　 （ｎ,ｒはともに非負整数で、　ｎ≧ｒ.　※このｎとｒの条件は以降ことわりなく用いる。）
ここでｎ！は「ｎの階乗」であり、
　　　ｎ！≡1×2×3×・・・・・×ｎ　　,　0！≡1
である。

（２．　また、ｎ個の要素から重複を許して選び、ｒ個並べる場合の数は、ｎｒ通りある。
　　　　（並べるｒ個のそれぞれにｎ通りずつの選び方があるので、ｎをｒ回かければよい）

さて本問の条件は、
「６個のマスのうち赤いマスがｒ個あるとする。 　赤のマスはそれぞれ、赤以外の（６－ｒ）個のマスの隣にできる （６－ｒ＋１）個の場所のいずれか１つずつのみ存在する」
と言い換えることができる。

具体的にｒ＝3のときを図示する。赤以外の2色のいずれかで塗られたマスは6-ｒ＝6-3＝3個存在し、 これを”＊”で表すと、
残り3個の赤のマスは図の"＿"の部分の4箇所（6－ｒ＋1）のうちいずれかに1つずつ入れれば赤いマスは連続しない。

　　＿＊＿＊＿＊＿　

赤で塗られるマスは （１．より6－ｒ＋1Ｃｒ＝4Ｃ3＝4通りあり、かつ、 赤以外で塗られたマスの場合の数は（２．より、26－ｒ＝23＝8通りある。
よって、ｒ＝3の時、条件を満たす塗り分け方は4×8＝32通りあることがわかる　・・・①
ところが、ｒ≧4のときは（6－ｒ＋1）＜4　であり、6－ｒ＋1Ｃｒは（１．で挙げたｎ≧ｒの条件を満たさないので不適である。
（このことは、赤いマスが4個以上のときは必ず赤いマスが連続することを意味する。）
したがって、0≦ｒ≦3の範囲で場合分けを行い、同様の手続きをすればよいことになる。
ⅰ) ｒ＝3のとき
　　これは前述した。①より32通り。
ⅱ)　ｒ＝2のとき
　　赤を塗る場合の数は 6－ｒ＋1Ｃｒ＝5Ｃ2＝10
　　かつ、赤以外の2色を塗り分ける場合の数は26－ｒ＝24＝16
　　10×16＝160　（通り）
ⅲ) r＝1のとき
　　赤を塗る場合の数は 6－ｒ＋1Ｃｒ＝6Ｃ1＝6
　　かつ、赤以外の2色を塗り分ける場合の数は26－ｒ＝25＝32
　　6×32＝192　（通り）
ⅳ）　ｒ＝０のとき
　　このときは、赤以外の2色を重複を許して6つ塗り分ける場合の数となるので、
　　26＝64　（通り）
ⅰ）～ⅳ）より、題意を満たす塗り分け方の場合の数は
　　32＋160＋192＋64＝448　（通り）　　・・・[答]

＃　因みに、この結果は、条件を与えないで3色を塗り分ける場合の数
　　36＝729　（通り）　の約61.5％に相当する。

解答・その13

（ペンネ－ム：Ｎと～）

答　４４８通り
まず、赤の塗り方が何通りあるか考える。
　　赤が０マスの場合………１とおり。
　　赤が１マスの場合………６とおり。
　　赤が２マスの場合……１０とおり。[6C2-5=10]
　　赤が３マスの場合………４とおり。
続いて、それぞれの場合の白黒の塗り方を考える。
　　赤が０マス……２の６乗で６４とおり。
　　赤が１マス……２の５乗で３２とおり。その６倍……１９２とおり。
　　赤が２マス……２の４乗で１６とおり。その１０倍…１６０とおり。
　　赤が３マス……２の３乗で８とおり。その４倍…………３２とおり。
全部あわせて
　　６４＋１９２＋１６０＋３２＝４４８（とおり）

解答・その14

（ペンネ－ム：転位反応）

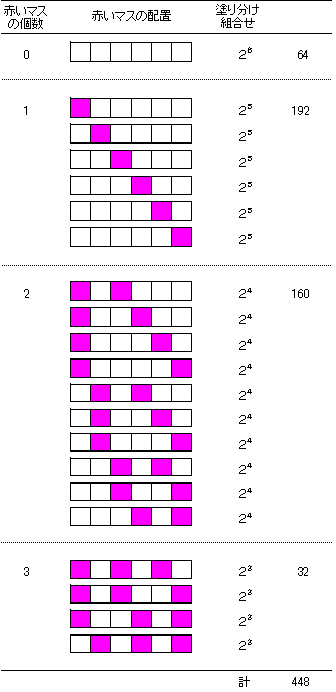
赤いマスの個数に応じて、それらが連続しない配置を全て書き下し、それぞれの場合について、残りのマスを白又は黒で塗り分ける組合せを数え上げれば良い。
なお、赤いマスが４個の場合、少なくとも二つのマスが連続するため、それ以上の個数の場合については考える必要は無い。よって、題意の塗り分け方は４４８通り。



解答・その15

（ペンネ－ム：haya）

塗り分け方は 448 通りです。

【解き方】
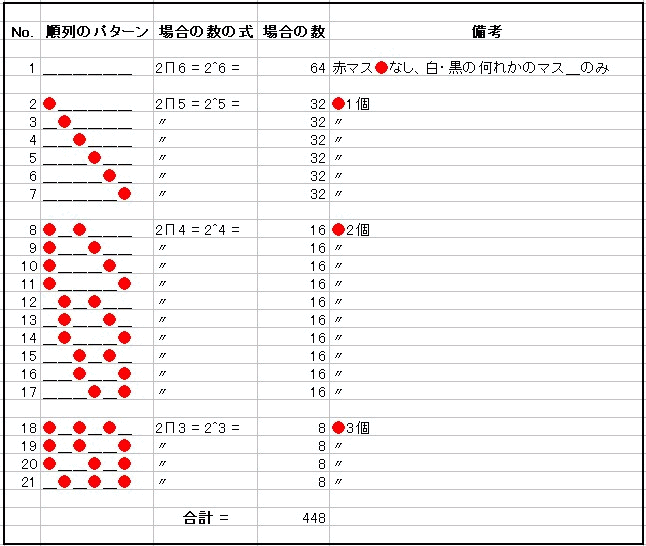
赤マス ● は連続して配置できない制限があるのでその限定されたパターンを先ずリストアップし、 それぞれに対して白・黒のマス ＿ の順列の数を求めて合計する。



解答・その16

（ペンネ－ム：夜ふかしのつらいおじさん）

赤いマスが隣り合わない塗り分け方を数えるのに、 赤いマスの個数で場合分けをします。

※　４個以上の場合はありません。
∴　６４＋１９２＋１６０＋１６＝４３２通り。
なお、６個のマスを赤、白、黒のいずれかの色で塗り分ける方法は、３6＝７２９通りあります。

残り赤が連続する場合を補って確かめておきます。
赤のマスの個数で場合分けをします。

top