栤戣159丂惓曽宍偺栤戣
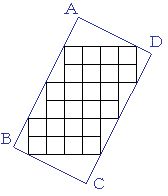
壓偺挿曽宍ABCD偺柺愊傪媮傔偰偔偩偝偄丅 偨偩偟丄挿曽宍偺拞偺24屄偺仩偼偡傋偰侾曈偑侾cm偺惓曽宍偱偡丅
栤戣偺弌揟
嶼悢僆儕儞僺僢僋偵挧愴
嶼悢僆儕儞僺僢僋埾堳夛曇
島択幮僽儖乕僶僢僋僗
2007擭僩儔僀傾儖栤戣
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗嵞弌敪乯
摎偼 36cm2
夝摎丒偦偺2
乮儁儞僱亅儉丗昹揷丂柧枻乯
乮儁儞僱亅儉丗僆儎僕乯 挿曽宍撪偵桳傞俀係屄偺惓曽宍偺梋敀偵偱偒傞丄憡帡側捈妏嶰妏宍偺戝偒偄傎偆偺塻妏傪
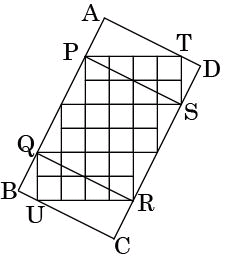
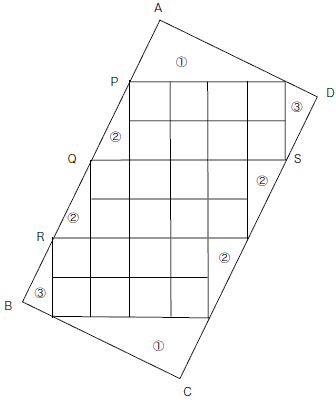
AD亖丂 乮儁儞僱亅儉丗柪巕偺梇擫乯 乮儁儞僱亅儉丗挿嶈搰尨偐偑傒乯 乮儁儞僱亅儉丗僗儌乕僋儅儞乯 摎偊丂俁俇cm2丂偱偡丅 乮儁儞僱亅儉丗岼偺柌乯 乮儁儞僱亅儉丗儅僆乯 恾偺4揰P丆Q丆R丆S傪寢傫偱偱偒傞巐妏宍PQRS偵偍偄偰丄
PQ丆QR偼偦傟偧傟椬曈偑1丗2偺捈妏嶰妏宍偺幬曈偵偁偨傞偺偱丄
挿曽宍PQRS偼惓曽宍偱偁傞丅 挿曽宍ABCD偺柺愊偼丄AB亊BC = (AP+PQ+QB)亊BC
= (b+a+b)亊a
= a亊b + a亊a + a亊b
(仸1),(仸2)傛傝
= 8 + 20 + 8
= 36
乮儁儞僱亅儉丗僔儏儗乕僨傿儞僈乕偺嶰栄擫乯 乮儁儞僱亅儉丗URU乯 乮儁儞僱亅儉丗falcon@拞妛嫵巘乯 俁俇們倣2 亙峫偊曽亜 俴偲俽偺憡帡斾偼俀丗侾偱偁傞偨傔丄捈妏傪嫴傓俀曈偺斾偑侾丗俀偱偁傞偙偲偐傜丄
俴偲俽傪俀偮偢偮慻傒崌傢偣傞偙偲偱丄廲俀噋丄墶係噋偺挿曽宍俴仌俽傪嶌傞偙偲偑偱偒傞丅乮恾俀嶲徠乯 偟偨偑偭偰丄 乮儁儞僱亅儉丗T_Tatekawa乯 夝摎俀 乮儁儞僱亅儉丗偺偭偙傫乯 (1)PQ傪幬曈偲偡傞捈妏嶰妏宍偲QR傪幬曈偲偡傞捈妏嶰妏宍傪偁傢偣傞偲 (2)摨條偵丂TU傪幬曈偲偡傞捈妏嶰妏宍偲UV傪幬曈偲偡傞捈妏嶰妏宍傪偁傢偣傞偲 (3)PQ傪幬曈偲偡傞捈妏嶰妏宍偲仮RSB偼憡帡偱丄憡帡斾偼併俆丗俀丄柺愊斾偼俆丗係偲側傞偐傜
丂仮RSB偲仮VWD傪偁傢偣傞偲 (4)仮RSB偲仮WPA偼憡帡偱丄憡帡斾偼侾丗俀丄柺愊斾偼侾丗係偲側傞偐傜
仮WPA偲仮STC傪偁傢偣傞偲 乮儁儞僱亅儉丗嶰妏掕婯乯 乮儁儞僱亅儉丗僶儖僞儞惎恖乯 峫偊曽丗 乮儁儞僱亅儉丗揮埵斀墳乯 乮儁儞僱亅儉丗teki乯 摎偊丂丂丂俁俇cm2 乮儁儞僱亅儉丗傗側偣乯 夝朄偦偺侾 乮儁儞僱亅儉丗namiusagi乯 丂嘆嘇嘊偼偡傋偰憡帡宍乮廲俀丗墶侾偺捈妏嶰妏宍乯偱丄
嘆偺柺愊偼16/5丄嘇偺柺愊偼1丄嘊偺柺愊偼4/5偵側傝丄嘋(惓曽宍1*1)偼俀係屄偱
柺愊偼嘆*2+嘇*4+嘊*2+嘋*24=(32/5)+4+(8/5)+24=36(cm2) 乮儁儞僱亅儉丗haya乯 亂夝偒曽亃 乮儁儞僱亅儉丗ykak乯 乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯 摎偊偼丄俁俇偱偡丅 乮儁儞僱亅儉丗俽俷倀乯 (1)丂怓傪偮偗偨嶰妏宍偼慡偰憡帡 俀偮埲忋偺嶰妏宍傪慻傒崌傢偣偨傝丄憡帡偺娭學傪偆傑偔棙梡偟偰柺愊傪媮傔傞偙偲偑偱偒傑偡偹丅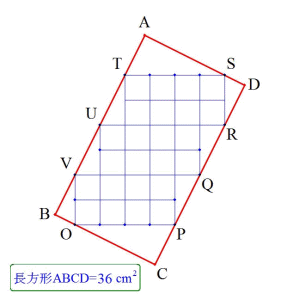 僌儔僼嶌惉僜僼僩俧俼俙俹俤偱夝摎偟偨丏
僌儔僼嶌惉僜僼僩俧俼俙俹俤偱夝摎偟偨丏
捈慄俠俢偼丆捈慄俹俻偲側傞偺偱丆偙偺曽掱幃傪倗(倶)亖俀(倶亅俀)偲偡傞丏
俙俛佦俛俠偐傜丆捈慄俛俠丆俙俢偺孹偒偼亅侾乛俀偲側傞丏
捈慄俛俠偺曽掱幃傪倛(倶)亖亅倶乛俀偲偡傞丏
捈慄俙俢偺曽掱幃傪倖1(倶)亖亅(倶亅俇)乛俀亄俇偲偡傞丏
俙偺倶嵗昗偼丆曽掱幃倖(倶)亖倖1(倶)偺夝丆
俛偺倶嵗昗偼丆曽掱幃倖(倶)亖倛(倶)偺夝丆
俠偺倶嵗昗偼丆曽掱幃倗(倶)亖倛(倶)偺夝丆
俢偺倶嵗昗偼丆曽掱幃倗(倶)亖倖1(倶)偺夝
偲側傞偺偱丆俙乣俢偺嵗昗傪寁嶼偱媮傔傜傟傞乮sol娭悢乯丏
俙俛偺挿偝乮len娭悢乯偲俛俠偺挿偝偺愊偑媮傔傞柺愊偱偁傞丏
摎偼俁俇們倣俀偱偁傞丏
夝摎丒偦偺3
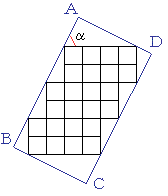
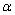 偲偡傞偲丄
偲偡傞偲丄
丂丂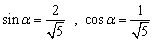
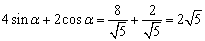 丒丒丒乮嘥乯
丒丒丒乮嘥乯
AB亖丂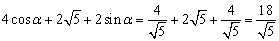 丒丒丒(嘦)
丒丒丒(嘦)
乮嘥乯丆乮嘦乯傛傝
丂丂俽亖俙俢亊俙俛亖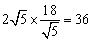
亪丂俁俇們倣2
夝摎丒偦偺4
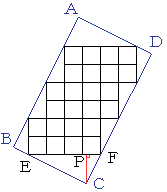 挿曽宍偺曈俛俠忋偱丄挿曽宍偺拞偺24屄偺仩偲愙偟偰偄傞揰傪俤丄
挿曽宍偺曈俠俢忋偱丄挿曽宍偺拞偺24屄偺仩偲愙偟偰偄傞揰傪俥丄
捀揰俠偐傜捈慄俤俥偵偍傠偟偨悅慄偺懌傪俹偲偡傞丅
挿曽宍偺曈俛俠忋偱丄挿曽宍偺拞偺24屄偺仩偲愙偟偰偄傞揰傪俤丄
挿曽宍偺曈俠俢忋偱丄挿曽宍偺拞偺24屄偺仩偲愙偟偰偄傞揰傪俥丄
捀揰俠偐傜捈慄俤俥偵偍傠偟偨悅慄偺懌傪俹偲偡傞丅
挿曽宍偺拞偺24屄偺仩偺曈偑丄倃丒倄幉偲暯峴偵側傞傛偆偵丄倃丒倄幉傪掕傔傞丅
偙偺偲偒丄挿曽宍偺拞偺仩偲愙偟偰偄傞嬶崌偐傜峫偊偰丄
曈俠俢偼倃幉偺惓曽岦偵侾扨埵堏摦偡傞偲丄倄幉偺惓曽岦偵俀扨埵堏摦偡傞傛偆偵
孹偄偰偄傞偺偱丄曈俛俠偼倃幉偺惓曽岦偵俀扨埵堏摦偡傞偲丄
倄幉偺晧曽岦偵侾扨埵堏摦偡傞傛偆偵孹偄偰偄傞偲偄偆偙偲偵側傞丅
偙偺偙偲傛傝丄PF丄PC丄EP偺挿偝偵偮偄偰丄埲壓偺幃偑惉傝棫偮丅
丂丂PF:PC=1:2
丂丂EP:PC=2:1
丂丂EP+PF=4
偙傟傪夝偄偰
丂丂PC=2PF
丂丂2PC=EP
丂丂2PC=4PF
丂丂EP=4PF
丂丂EP=4-PF
丂丂4PF=4-PF
丂丂5PF=4
丂丂PF=4/5
丂丂PC=8/5
傛偭偰嶰妏宍俤俠俥偺柺愊偼4*(8/5)/2=16/5
捀揰俛丆俢晅嬤偺嶰妏宍傕丄嶰妏宍俤俠俥偲憡帡偱偁傞偺偱丄
乮掙曈偑敿暘丄崅偝偑敿暘側偺偱柺愊偑1/4乯柺愊偼4/5
捀揰晅嬤偺嶰妏宍偺柺愊(16+4)*2/5=8
曈俙俛丆俠俢忋偵偁傞嶰妏宍係屄偺柺愊4*(1*2/2)=4
挿曽宍偺拞偺24屄偺仩偺柺愊24
挿曽宍俙俛俠俢偺柺愊偼丄忋婰偺柺愊偺崌寁36
夝摎丒偦偺5
 嶰暯曽偺掕棟傪棙梡偡傞偲
嶰暯曽偺掕棟傪棙梡偡傞偲
挿曽宍偺挿偄曽偺曈偼 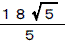 丆
抁偄曽偺曈偼
丆
抁偄曽偺曈偼  偲側傞偺偱丆
偲側傞偺偱丆
柺愊偼俁俇cm2偵側傞丅
亂摎亃丂俁俇cm2
夝摎丒偦偺6
 巆傝偺晹暘傪拞偺惓曽宍偵憡摉偡傞傛偆偵悢偊傟偽偄偄偲...
巆傝偺晹暘傪拞偺惓曽宍偵憡摉偡傞傛偆偵悢偊傟偽偄偄偲...
10屄暘+2屄暘*3=16屄丄拞偵24屄偁傞偺偱...
丂丂丂2*2+((2/併5)2+(4/併5)2)*2+24=4+8+24=36 cm2
偵側傞偺偐側...^^?
夝摎丒偦偺7
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
恾傪憓擖偟偰壓偝偄
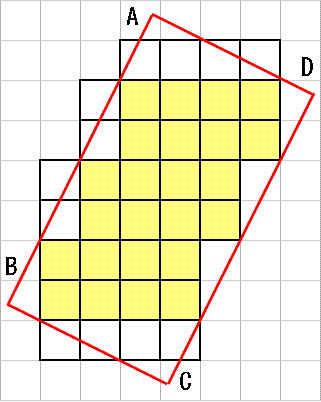
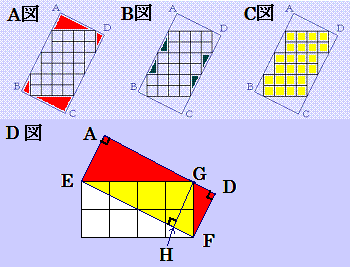
A恾偺愒怓晹暘偺柺愊亖俀噋亊係噋亖俉cm2
B恾偺惵怓晹暘偺柺愊亖侾噋亊俀噋亊俀亖俀cm2
C恾偺墿怓晹暘偺柺愊亖係噋亊俀噋亊俁亖俀係cm2
崌寁ABCD偺挿曽宍偺柺愊亖俉cm2亄俀cm2亄俀係cm2亖俁俇cm2
D恾偼愒怓晹暘偺柺愊偑係噋亊俀噋亖俉cm2偺敿暘偱偁傞徹柧偱偡丅
慄暘AD偲愙偡傞揰傪G偲偡傞丄G偐傜慄暘EF偵悅捈偵壓偟偨岎揰傪H偲偡傞丅
柺愊儮EGF=柺愊儮EAG+柺愊儮DFG偺徹柧
丂佢EAG亖佢EHG=亖佢GDH=俋侽亱偳捈妏偱偡丅
丂儮EAG傕儮DFG傕嶰妏宍偺崅偝偼GH偱摨偠偱偡丅
丂儮FDG=儮FHG傕堦曈GF偑摨偠偱崌摨偱偡丅
廬偭偰柺愊儮EGF=柺愊儮EAG+柺愊儮DFG偱偁傞偙偲偑徹柧偱偒傑偡丅
夝摎丒偦偺8
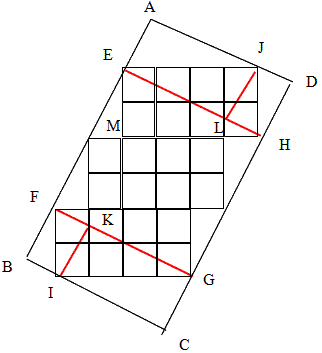 崱丄塃恾偵帵偡條偵挿曽宍偺曈AD偲BC奺乆偵暯峴側曈EH偲FG傪偦傟偧傟堷偔丅
崱丄塃恾偵帵偡條偵挿曽宍偺曈AD偲BC奺乆偵暯峴側曈EH偲FG傪偦傟偧傟堷偔丅
枖丄曈AB偲CD奺乆偵暯峴側曈IK偲JL傪堷偔丅懄偪丄4杮偺愒慄偲側傞丅
偙偙偱暯峴側曈偺嶖妏偼摍偟偄偺偱丄仮AEJ佭仮LJE枖丄仮DJH佭仮LHJ偱偁傞丅
懄偪丄仮AEJ+仮DJH亖仮EJH亖乮1/2乯丒挿曽宍EJHM亖乮1/2乯丒8亖4偲側傞丅仮GIF偵偮偄偰傕慡偔摨條側峫嶡偐傜柺愊偼4偲側傞丅
枖丄挿曽宍EFGH撪偵墬偗傞4屄偺嶰妏宍偺柺愊偼奺乆1偱偁傞偐傜丄崌寁偱4偲側傞丅
場偭偰丄媮傔傞挿曽宍偺柺愊偼丄24+4+8亖36偱偁傞丅
夝摎丒偦偺9
 夝摎丗36 cm2
夝摎丗36 cm2
偦偺柺愊偼1曈1cm偺惓曽宍16屄暘 + 掙曈1cm,崅偝2cm偺嶰妏宍4屄暘側偺偱
16+4=20 偲側傞丅
傛偭偰丄惓曽宍PQRS偺1曈偺挿偝傪a偲偡傞偲(PQ=QR=a)丄a亊a=20 乧 (仸1)
仮TPS偵偍偄偰偦偺柺愊偼丄TS亊TP亐2 = 2亊4亐2 = 4
PS傪掙曈偵峫偊偨偲偒丄崅偝偼AP偲側傞偺偱丄AP=b偲偡傞偲(摨條偵QB=b)丄
PS亊AP亐2 = a亊b亐2 = 4
傛偭偰丄a亊b = 8 乧 (仸2)
夝摎丒偦偺10
 摎丗36(cm2)
摎丗36(cm2)
仭夝朄
亙曽恓亜丂
丒憡帡斾傪梡偄偰嶰妏宍偺晹暘偺柺愊傪媮傔傞丅
挿曽宍ABCD偲丄24屄偺惓曽宍偺夠偲偵嫴傑傟偰偱偒傞8偮偺嶰妏宍偵偮偄偰峫偊傞丅
偙傟傜偑偡傋偰捈妏嶰妏宍偲側偭偰偄傞偙偲偼恾偐傜柧傜偐偱偁傞丅丂丒丒丒(1)
傑偨丄偳偺捈妏嶰妏宍傕丄帺傜偺嶌傞曈傪娷傓挿曽宍ABCD偺曈忋偺堎側傞2揰偵偍偄偰
偦傟偧傟暿偺2偮偺捈妏嶰妏宍偲愙偟偰偍傝丄摨帪偵惓曽宍偺1捀揰偲傕愙偟偰偄傞忬懺偵偁傞丅
偙偙偱偙偺愙揰偺堦偮傪偲傞偲丄偙偺揰偼惓曽宍偺捀揰偲愙偟偰偄傞偺偱丄
惓曽宍傪嫴傓2偮偺捈妏嶰妏宍偺2妏偺榓偼
丂丂丂180-90亖90乮搙乯
偲側傞丅
偡側傢偪丄偙偺愙揰傪嫟桳偡傞2偮偺捈妏嶰妏宍偺妏偺偆偪丄堦偮偺嶰妏宍偺捀妏偺妏搙傪壖偵乽仠乿偲偍偒丄
傕偆堦偮偺捈妏嶰妏宍偺愙偡傞捀妏偺妏搙傪壖偵乽亊乿偲偍偔偲偡傞偲丄
乽仠乿亄乽亊乿亖90乮搙乯偱偁傞丅丂丒丒丒(2)
堦曽丄嶰妏宍偺撪妏偺榓偼180搙側偺偱捈妏偱側偄巆傝偺撪妏偺榓偼90搙偲側傞偨傔丄
(2)傛傝丄愙揰偺捀妏偑乽仠乿偺偲偒丄摨偠嶰妏宍偺梋傝偺妏偼乽亊乿丅
媡偵愙揰偺捀妏偑乽亊乿偺偲偒偼梋傝偺妏偼乽仠乿偲側傞偙偲偑暘偐傞丅
偲偙傠偱丄偼偠傔偵弎傋偨傛偆偵丄偙偺娭學偼挿曽宍ABCD偺曈忋偺偳偺嶰妏宍偺捀揰偵偮偄偰傕惉傝棫偭偰偄傞偺偱丄
8偮偺捈妏嶰妏宍偺丄捈妏偱側偄2妏偺妏搙偼偦傟偧傟乽仠乿偍傛傃乽亊乿偲側傞丅丒丒丒(3)
(1)丄(3)傛傝丄8偮偺捈妏嶰妏宍偼屳偄偵憡帡偱偁傞乮擇妏憡摍乯丅丂丒丒丒(4)
偝傜偵恾傛傝丄挿曽宍ABCD偺捀揰傪娷傑側偄4偮偺捈妏嶰妏宍偼捈妏傪嫴傓擇曈偺挿偝偑偦傟偧傟1cm丄2cm偲
摍偟偔側偭偰偍傝丄偙傟傜偺4偮偺捈妏嶰妏宍偼屳偄偵崌摨偱丄柺愊偼偦傟偧傟
丂丂丂1亊2亐2亖1丂乮cm2乯
偱偁傝丄幬曈偺挿偝偼嶰暯曽偺掕棟傛傝丄
丂丂丂併乮12亄22乯亖併5丂乮cm乯丂丒丒丒(5)
傑偨丄挿曽宍偺捀揰A傑偨偼捀揰C傪娷傓2偮偺捈妏嶰妏宍偼幬曈偑偦傟偧傟4cm偲屳偄偵摍偟偔崌摨偱偁傝丄丒丒丒(6)
摨條偵捀揰B傑偨偼捀揰D傪娷傓2偮偺捈妏嶰妏宍傕幬曈偑偦傟偧傟2cm偲屳偄偵摍偟偔崌摨偱偁傞丅丒丒丒(7)
偝偰丄(4)傛傝丄(5)(6)(7)偱嫇偘偨嶰妏宍偺慻偺幬曈偺憡帡斾偼偦傟偧傟
丂丂丂併5丗4丗2
偲側傞偺偱丄柺愊斾偼奺乆2忔偟偰
丂丂丂5丗16丗4
偲側傞丅
(5)偱嫇偘偨捈妏嶰妏宍偺柺愊偑1cm2 偩偭偨偺偱丄5偱彍偡傞偲cm2扨埵偱偺柺愊斾
丂丂丂1丗(16/5)丗(4/5)
傪摼傞丅
8偮偺捈妏嶰妏宍偺柺愊偺榓偼
丂丂丂1亊4亄(16/5)亊2亄(4/5)亊2亖12(cm2)
偙偙偵惓曽宍24屄偺柺愊24cm2傪懌偟偰丄
挿曽宍ABCD偺柺愊傪
丂丂丂12亄24亖36(cm2)
偲摼傞丅
夝摎丒偦偺11
 掙曈亖1丂崅偝亖2丂偵懳偡傞幬曈偺挿偝偼併12+22亖併5
偱偁傞偺偱嬻敀売強偺嶰妏宍偺嶰曈斾棪偼1丗2丗併5偱偁傞丅
掙曈亖1丂崅偝亖2丂偵懳偡傞幬曈偺挿偝偼併12+22亖併5
偱偁傞偺偱嬻敀売強偺嶰妏宍偺嶰曈斾棪偼1丗2丗併5偱偁傞丅
曈A-B亖4/併5+併5+併5+4/併5
丂丂丂亖2併5+8/併5
丂丂丂亖乮10+8乯/併5
丂丂丂亖18/併5
曈A-D亖8/併5+2/併5
丂丂丂亖乮8+2乯/併5
丂丂丂亖10/併5
挿曽宍ABCD亖18/併5亊10/併5
丂丂丂丂丂亖180/5
丂丂丂丂A=36cm2偲側傞丅
夝摎丒偦偺12
24屄偺仩偺廃傝偵偱偒偰偄傞捈妏嶰妏宍偼慡偰憡帡偱偁傝丄捈妏傪嫴傓2曈偺斾偼侾丗俀丅
戝偒偝偑俁庬椶偁傞偺偱丄戝偒偄曽偐傜俴丆俵丆俽偲柤慜傪偮偗偰偍偔丅乮恾侾嶲徠乯
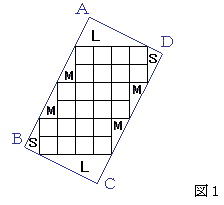
傑偨丄俵傪俀偮傪慻傒崌傢偣偰廲俀噋丄墶侾噋偺挿曽宍俵仌俵傪嶌傞偙偲偑偱偒傞丅乮恾俁嶲徠乯
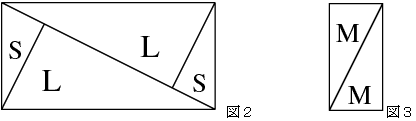
挿曽宍俙俛俠俢偺柺愊亖仩俀係屄偺柺愊 亄 俴仌俽偺柺愊 亄 俵仌俵偺柺愊 亊 俀
丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀係們倣2 亄 俉們倣2 亄 俀們倣2亊 俀
丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俁俇們倣2
夝摎丒偦偺13
 夝摎侾
夝摎侾
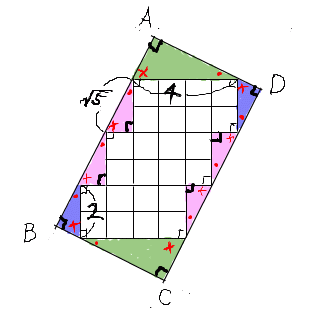
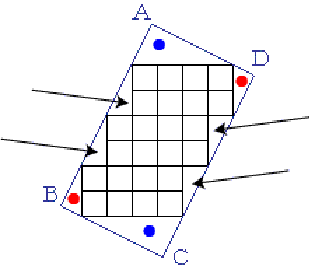
揧晅偺恾偺傛偆偵丆惓曽宍埲奜偺偲偙傠偵拝栚偟傑偡丏
栴報偱帵偟偨巐偮偺捈妏嶰妏宍偼丆捈妏傪嫴傓曈偺挿偝偑 1cm, 2cm 偱偡丏
4偮崌傢偣偰柺愊偼 1x2 / 2 x4 = 4 cm2 偱偡丏
屻偼惵偄揰偲愒偄揰傪懪偭偨嶰妏宍傪峫偊傑偡丏
偙傟傜偺嶰妏宍偱丆捈妏埲奜偺偲偙傠偵拝栚偟傑偡丏
椺偊偽慄暘AD偺搑拞偱惓曽宍偑愙偡傞帠偵傛傝丆擇偮偺嶰妏宍偑嬫愗傜傟傞
栿偱偡偑丆偙偺愙揰偱岦偐偄崌偆擇偮偺嶰妏宍偺妏偺妏搙偺榓偼90搙偱偡丏
偡傞偲丆慄暘AD傪娷傓嶰妏宍偱丆慄暘AD忋偵側偄偦傟偧傟偺妏偺妏搙偺榓傕
90搙偲偄偆帠偵側傝傑偡丏
偮傑傝丆捀揰D傪娷傓彫偝偄嶰妏宍傪暯峴堏摦偟丆捀揰D偲捀揰A傪廳偹傞偲丆
戝偒側捈妏嶰妏宍偑弌棃傑偡丏偙偺捈妏嶰妏宍偺丆捈妏傪嫴傓晹暘偺曈偺
挿偝偼 2cm, 4cm 偱偡丏
慄暘 BC 偺懁偺擇偮偺嶰妏宍傕摨條偵峫偊傑偡丏
惵偄揰偲愒偄揰傪懪偭偨嶰妏宍偺柺愊偺崌寁偼丆
丂丂2x4 / 2 x 2 = 8 cm2
偱偡丏
傕偲傕偲柺愊偑暘偐偭偰偄傞惓曽宍偺柺愊傪懌偡偲丆慡懱偺挿曽宍偺柺愊偑
傢偐傝傑偡丏
丂丂24 + 4 + 8 = 36 cm2
揧晅偺恾偺栴報偱巜偟帵偟偨嶰妏宍偼丆捈妏嶰妏宍偱偡丏
幬曈偺挿偝偼 併(12+22) = 併5 cm 偱偡丏
師偵惵偄揰丆愒偄揰傪懪偭偨嶰妏宍傪峫偊傑偡偲丆偙傟傜偺妏偼栴報傪
偮偗偨嶰妏宍偺妏偺堦偮偲丆捈妏傪嫴傫偱岦偐偄崌偄傑偡丏
惵偄揰丆愒偄揰傪懪偭偨嶰妏宍偼挿曽宍偺捀揰偺堦偮傪娷傓偺偱丆
偙傟傜偼捈妏嶰妏宍偱偡丏
偡傞偲丆惵偄揰丆愒偄揰傪懪偭偨嶰妏宍偼丆栴報偱巜偟帵偟偨嶰妏宍偲
憡帡偵側傝傑偡丏
憡帡斾偼
丂丂惵偄揰偺嶰妏宍丗栴報偺嶰妏宍丗愒偄揰偺嶰妏宍亖 4 : 併5 : 2
慄暘AD偺挿偝偼
丂丂4 x 2/併5 + 2 x 1/併5 = 10/併5 = 2 併5 cm
慄暘AB偺挿偝偼
丂丂2併5 + 4 x 1/併5 + 2 x 2/併5 = 18/併5 cm
傛偭偰挿曽宍偺柺愊偼
丂丂18/併5 x 2併5 = 36 cm2
夝摎丒偦偺14
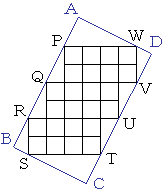 AB忋偺俁揰傪A偵嬤偄曽偐傜P,Q,R,
BC忋偺揰傪S,
CD忋偺俁揰傪C偵嬤偄曽偐傜T,U,V,
DA忋偺揰傪W偲偡傞
AB忋偺俁揰傪A偵嬤偄曽偐傜P,Q,R,
BC忋偺揰傪S,
CD忋偺俁揰傪C偵嬤偄曽偐傜T,U,V,
DA忋偺揰傪W偲偡傞
丂侾亊俀亖俀乮cm2)偺挿曽宍偵側傞
丂侾亊俀亖俀乮cm2)偺挿曽宍偵側傞
丂俀亊係/俆亖侾.俇乮cm2乯偺挿曽宍偵側傞
丂侾.俇亊係亖俇.係乮cm2)偺挿曽宍偵側傞
傛偭偰ABCD偺柺愊偼丂俀丒俀亄侾.俇亄俇.係亄俀係亖俁俇乮cm2)
夝摎丒偦偺15
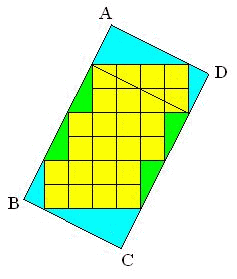 亂夝摎亃
亂夝摎亃
恾偺悈怓偺晹暘偺柺愊偼丆惓曽宍 8 屄暘
恾偺椢怓偺晹暘偺柺愊偼丆惓曽宍 4 屄暘
墿怓偺惓曽宍偑 24 屄偁傞偐傜
挿曽宍 ABCD 偺柺愊偼 36 cm2乧乵摎乶
夝摎丒偦偺16
 俁俇們倣2
俁俇們倣2
惓曽宍傪埻傓俉屄偺仮偼慡偰憡帡偱捈妏傪嫴傓曈偑侾丗俀偺捈妏嶰妏宍
忋壓偺係屄偺捈妏仮傪崌懱偝偣傞偲挿曽宍偵側傝
偦偺柺愊偼俀亊係偺挿曽宍偺敿暘偺俀攞偡側傢偪俉們倣2偵側傞丅
恀傫拞偺捈妏仮係屄偺柺愊偼奺侾們倣2偱係們倣2
惓曽宍俀係們倣2偵懌偡偲俁俇們倣2
夝摎丒偦偺17
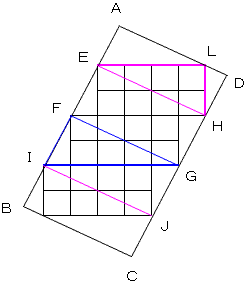 挿曽宍俙俛俠俢偺曈俙俢丄俛俠偵懳偟偰暯峴偵丄慄暘俤俫丄俥俧丄俬俰傪堷偔偙偲偑偱偒傞丅
挿曽宍俙俛俠俢偺曈俙俢丄俛俠偵懳偟偰暯峴偵丄慄暘俤俫丄俥俧丄俬俰傪堷偔偙偲偑偱偒傞丅
挿曽宍俥俬俰俧偺柺愊偼仮俥俬俧偺柺愊偺俀攞偱偁傞偙偲偐傜丄
挿曽宍俥俬俰俧偺柺愊偼丄乮俆亊俀亐俀乯亊俀亖侾侽
摨條偵丄挿曽宍俤俥俧俫偺柺愊偼侾侽
堦曽丄
挿曽宍俙俤俫俢偺柺愊偼仮俤俫俴偺柺愊偺俀攞偱偁傞偙偲偐傜丄
挿曽宍俙俤俫俢偺柺愊偼丄乮係亊俀亐俀乯亊俀亖俉
摨條偵丄挿曽宍俬俛俠俰偺柺愊偼俉
亪挿曽宍俙俛俠俢偺柺愊偼丄侾侽亄侾侽亄俉亄俉亖俁俇
夝摎丒偦偺18
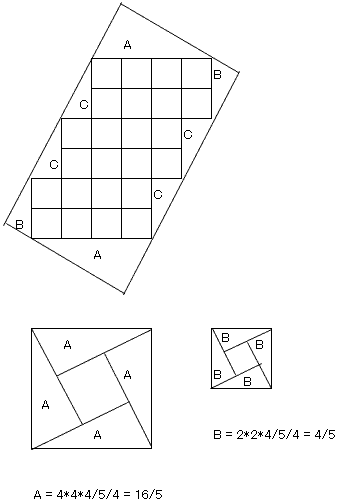
惓曽宍俀係屄偐傜偼傒弌偨晹暘偺柺愊傪峫偊傑偡丅
恾偺俠偺晹暘偼丄寁嶼偑娙扨偱丄侾cm2偱偡丅乮侾亊俀亐俀乯
偙傟偑係偮偱丄係cm2丅
栤戣偼丄俙偲俛偺晹暘偱偡偑丄柺敀偄曽朄偱寁嶼偱偒傑偡丅
俙傕俛傕摨偠偱偡偑丄偙傟傜傪係偮暲傋傞偲丄恀傫拞偵寠偺奐偄偨惓曽宍偑偱偒傑偡丅
偙偺宍丄weekend mathematics偺忢楢偵偼丄夰偐偟偄宍偱
恀傫拞偺惓曽宍偼慡懱偺柺愊偺1/5偵側傝傑偡偹丅
偱丄巆傝偺晹暘偺崌寁偼丄挌搙俉cm2偲側傝傑偡丅
尦偺俀係cm2偲崌傢偣偰丄俀係亄俉亄係亖俁俇cm2偱偡丅
夝摎丒偦偺19
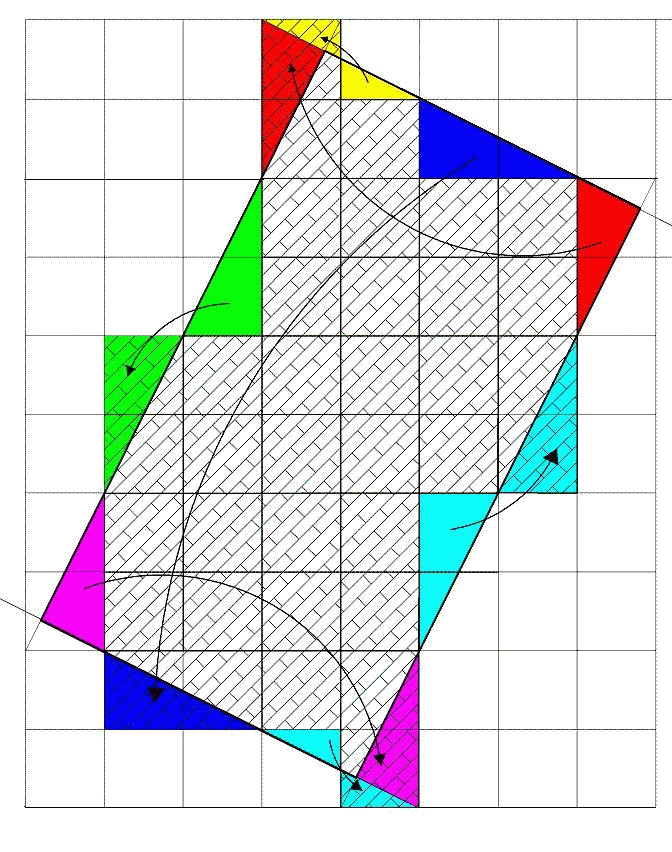
恾侾偺傛偆偵曗彆慄傪堷偄偰偐傜偱偡偑丄摨偠怓偺嶰妏宍傪堏摦偝偣傟偽
侾們倣偺惓巐妏宍偺廤傑傝偵廂傑傞偙偲偑夝傞丅屻偼偦偺悢傪悢偊傞偩偗偱
愮捁柾條偺惓巐妏宍傪悢偊傞偲俁俇屄桳傞偙偲偑夝傞丅
摎偊丂丂俁俇cm2
恾傪彂偄偰報嶞偟僴僒儈偱僠儑僉僠儑僉偟傑偟偨偗偳丂偱傕丄偙傟偭偰悢妛揑夝朄丠
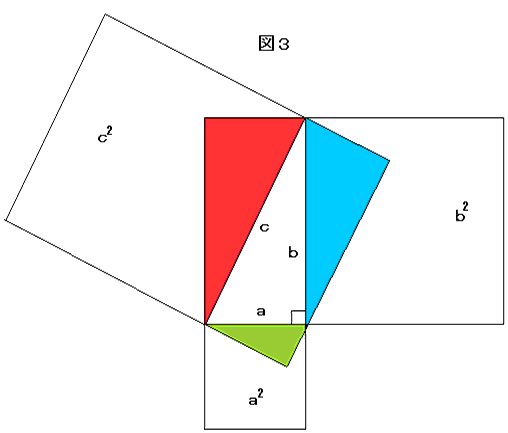
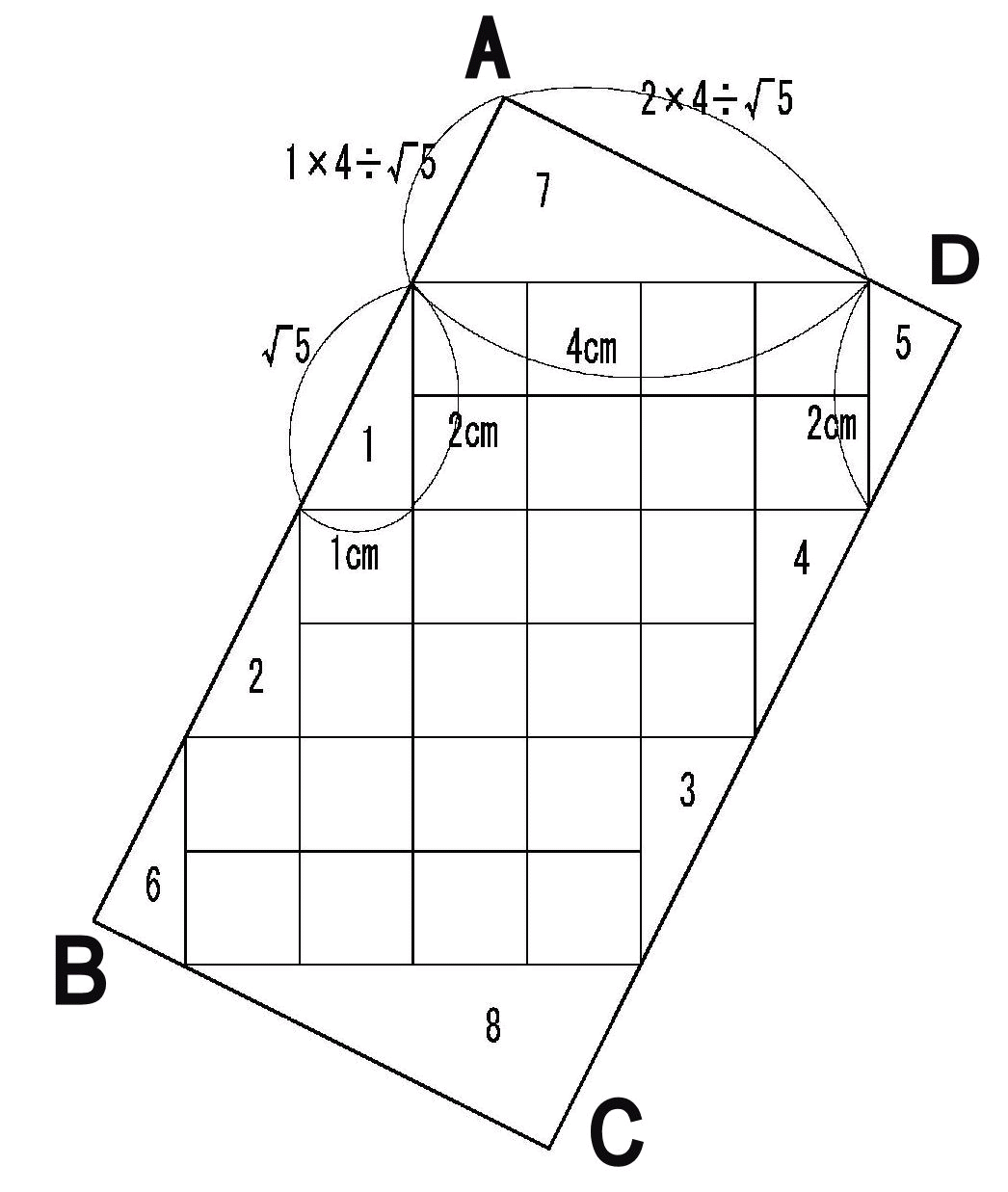 夝朄偦偺俀乮塃恾嶲徠乯
夝朄偦偺俀乮塃恾嶲徠乯
捈妏嶰妏宍 乮侾丏俀丏俁丏係乯偼摨宆丅丂乮俈丏俉乯偼摨宆丅丂乮俆丏俇乯偼摨宆偵側傞丅
傑偨捈妏嶰妏宍乮侾.俈.俆乯偼憡帡宍偵側傝丄偝傜偵嶰妏宍(俆)偺柺愊偼(俈)偺1/4偱桳傞偺偑夝傞丅
捈妏嶰妏宍 乮侾丏俀丏俁丏係乯偦傟偧傟偺柺愊偼恾俀偐傜傕夝傞傛偆偵侾們倣偺惓曽宍俀屄偺敿暘
偡側傢偪侾cm2偱偡丅
捈妏嶰妏宍乮俈.俉乯偦傟偧傟偺柺愊偼俉亐併5亊係亐併5亐俀亖乮俁俀亐侾侽乯cm2
偝傜偵捈妏嶰妏宍乯乮俆.俇乯偦傟偧傟偺柺愊偼乮俁俀亐係侽乯cm2
埲忋偐傜捈妏嶰妏宍柺愊憤崌寁傪媮傔傞幃偼
侾cm2亊係亄乮俁俀亐侾侽乯cm2亊俀亄乮俁俀亐係侽乯cm2亊俀亖侾俀cm2
巐妏宍俙丏俛丏俠丏俢偺柺愊偼侾c噓偺惓曽宍偑俀係屄偲捈妏嶰妏宍憤柺愊傪崌寁偡傟偽椙偄
俀係cm2亄侾俀cm2亖俁俇cm2
摎偊 俁俇cm2
偙偭偪偑悢妛揑偩側偀乣
夝摎丒偦偺20
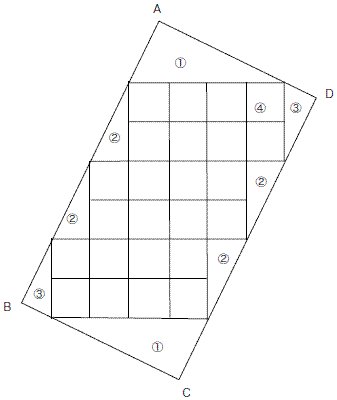
嘆嘇嘊偼偡傋偰憡帡宍乮廲俀丗墶侾偺捈妏嶰妏宍乯
AD:QS=2:併5 ,QS=5偐傜 AD=10/併5=2併5
AB=AP+PQ+QR+RS AP=4/併5=0.8併5,PQ=QR=併5,RB=0.8併5
AB=2*0.8併5+2*併5=3.6併5
柺愊偼AB*AD=(2併5)*3.6併5=7.2*5=36(cm2)
夝摎丒偦偺21
 挿曽宍ABCD偺柺愊偼 36 cm2 偱偡丅
挿曽宍ABCD偺柺愊偼 36 cm2 偱偡丅
(1) 1cm 妏偺惓曽宍偼24屄偱 24 cm2
(2) 慄暘AB媦傃CD偺搑拞偵偁傞4屄偺嶰妏宍偼2屄偢偮慻傒崌傢偣傞偲惓曽宍4屄暘丄偮傑傝 4 cm2
(3) 惓曽宍埲奜偺嶰妏宍偼壗傟傕曈偺斾偑 1:2:併5 偺憡帡側捈妏嶰妏宍側偺偱偁傞偑丄
丂A傪捀揰偲偡傞嶰妏宍媦傃C傪捀揰偲偡傞嶰妏宍傪2偮慻傒崌傢偣傞偲丄
丂擇曈偑丂4/併5 媦傃 8/併5 偺挿曽宍傪宍惉偡傞偐傜柺愊偼 32/5 cm2
丂摨條偵B丄D偼憡帡斾偑 1/2 側偺偱柺愊偼 8/5 cm2
傛偭偰丄媮傔傞柺愊 = (1) + (2) + (3) = 24 + 4 + 40/5 = 36 cm2
夝摎丒偦偺22
 夝摎丂俁俇們倣2
夝摎丂俁俇們倣2
奊偑偐偗側偄偺偱傕偳偐偟偄偱偡偑丅
俙俛俠俢偺拞偵偱偒傞嶰妏宍偼戝偒偝偑俁捠傝偁傝丄偙傟傪戝拞彫偲偡傞偲丄傑
偢偙傟偼慡偰憡帡宍偱偁傞偙偲偼偡偖暘偐傞丅
傑偨拞偺嶰妏宍偼掙曈乮堦墳抁偄曽傪掙曈偲偡傞乯侾們倣丄崅偝俀們倣偩偐傜柺愊偼侾們倣2
師偵俁捠傝偺嶰妏宍偺戝偒偝傪斾傋傞丅幬曈偵拲栚偡傞偲丄戝偺幬曈偼係們倣丄彫偺幬曈偼俀們倣偱偁傞偙偲偼柧傜偐丅
拞偼丄掙曈侾們倣丄崅偝俀們倣偩偐傜丄幬曈偼併俆們倣
戝拞彫偼慡偰憡帡宍偩偐傜丄偦偺柺愊斾偼曈偺挿偝偺斾偺俀忔偱丄係丗俆丗侾俇偲側傞丅
拞偺嶰妏宍偺柺愊偼侾們倣2偩偐傜丄忋偺柺愊斾傪尦偵寁嶼偡傞偲
彫偼係/俆們倣2丄戝偼侾俇/俆們倣2
俙俛俠俢偺柺愊偼丄侾曈偑侾們倣偺惓曽宍俀係屄暘偲丄戝俀屄丄拞係屄丄彫俀屄偺柺愊傪崌傢偣偨傕偺偵側傞丅
丂丂俀係丂亄丂侾俇/俆亊俀丂亄丂係丂亄丂係/俆亊俀丂亖丂俁俇
夝摎丒偦偺23
恾侾偺傛偆偵彫偝側惓曽宍偺暲傃偺忋偲壓丄塃偲嵍偺晹暘傪墑挿偟偰惓曽宍傪嶌傝傑偡丅
恾俀偺傛偆偵怓傪偮偗偨晹暘傪堏摦偟傑偡丅
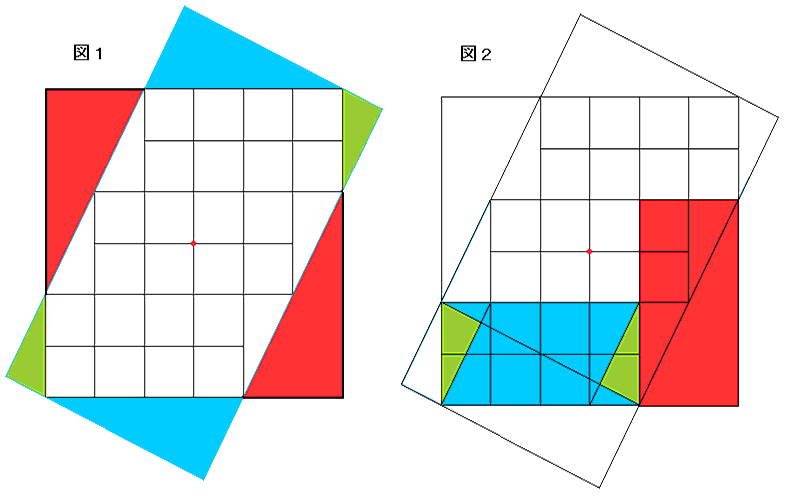
偡傞偲惵俀屄丄墿椢俀屄偺係屄偺捈妏嶰妏宍偺柺愊偺崌寁偑丄愒俀屄偺捈妏嶰妏宍偺柺愊偺崌寁偲摍偟偄偙偲偑暘偐傝傑偡丄
偙偺偙偲偼丄嶰暯曽偺掕棟乮僺僞僑儔僗偺掕棟乯偲摨偠偙偲偱偡丅
憡帡偺娭學偵偁傞暯柺恾宍偺柺愊偼懳墳偡傞曈偺挿偝偺俀忔偵斾椺偟傑偡丅
愒丄惵丄墿椢偺俁屄偺捈妏嶰妏宍偼憡帡偱偡丅
愒偺捈妏嶰妏宍偺奺曈偲俁屄偺捈妏嶰妏宍偺幬曈偑摨偠挿偝偱偡丅
傛偭偰丄乽愒亖惵亄墿椢乿偵側傝傑偡丅
夝摎丒偦偺24
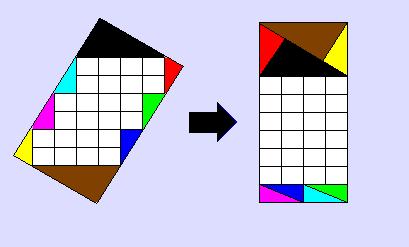
(2)丂幬曈偱側偄2曈偺挿偝偺斾偼1:2偲偄偆擇偮偺惈幙傪巊偆偲丄塃恾偺傛偆偵側傝丄柺愊偼36丂//
惓夝幰
namiusagi
栭傆偐偟偺偮傜偄偍偠偝傫
僶儖僞儞惎恖
僗儌乕僋儅儞
偺偭偙傫
嵞弌敪
T_Tatekawa
僆儎僕
falcon@拞妛嫵巘
儅僆
岼偺柌
柪巕偺梇擫
傗側偣
揮埵斀墳
ykak
teki
URU
忨偺偍偠偝傫
挿嶈搰尨偐偑傒
昹揷丂柧枻
僔儏儗乕僨傿儞僈乕偺嶰栄擫
嶰妏掕婯
haya
俽俷倀
僐儊儞僩
夝摎偲偲傕偵丄恾傪昤偄偰偛憲晅偄偨偩偄偨曽傕懡偔偍偄偱偱偟偨丅偳偆傕偁傝偑偲偆偛偞偄傑偟偨丅
 top
top