問題158 ピラミッドの問題
七段のピラミッドがあります。一段目の7つの( )に
1〜7の数字を1つずつ入れます。そうして隣どうしの( )の
中の数字をたしてその和を一つ上の( )に入れます。
同じようなたし算をしていき、いちばん上の( )まで
いけば終わりです。
問1
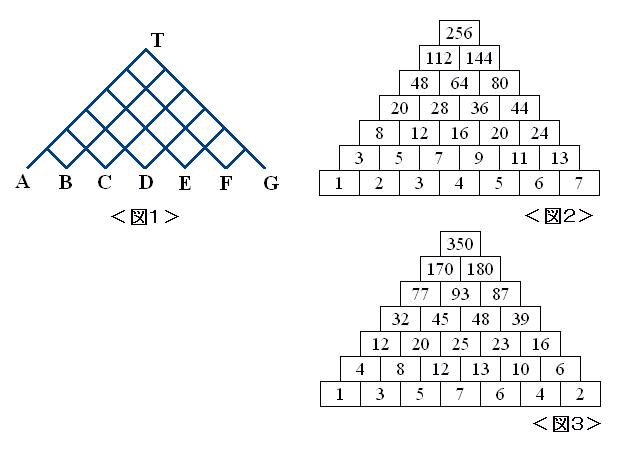
図1は何段のピラミッドの一番目に左から小さい順に1〜7を入れて、
途中まで規則通りにたし算をしたものです。
図1の七段目の(?)に入る数を求めなさい。
図1 (?) 七段目 ( )( ) 六段目 ( )( )( ) 五段目 ( )( )( )( ) 四段目 (8)(12)( )( )( ) 三段目 (3)(5)(7)( )( )( ) 二段目 (1)(2)(3)(4)(5)(6)(7) 一段目
問2
七段のピラミッドの一番上の( )の中の数を最大にするためには、
一段目の7つの( )に1〜7をどのような順で入れればよいですか。
問題の出典
算数オリンピックに挑戦
算数オリンピック委員会編
講談社ブルーバックス
2007年トライアル問題
答えと解説
解答・その1
(ペンネ−ム:浜田 明巳)
エクセルのマクロで解きました。
問1.256
問2.最大値は350で,並び方は次の8通り.
1 3 5 7 6 4 2
1 3 6 7 5 4 2
1 4 5 7 6 3 2
1 4 6 7 5 3 2
2 3 5 7 6 4 1
2 3 6 7 5 4 1
2 4 5 7 6 3 1
2 4 6 7 5 3 1
ようするに,真ん中を最大の7にして,左右に行くほど小さくすればいいようです.端になる程、足される回数が減るので,なるべく端に小さい数を持って来れば,一番上が最大となるのでしょう.
Option Explicit
Dim a(7, 7) As Integer
Sub Macro1()
Call mondai1(1)
Call mondai2(1)
End Sub
Sub mondai1(ByVal x As Variant)
Sheets("Sheet1").Select
Dim j As Integer
Dim jj As Integer
For j = 1 To 7
a(j, 1) = j
Next j
For j = 2 To 7
For jj = 1 To 7 - (j - 1)
a(jj, j) = a(jj, j - 1) + a(jj + 1, j - 1)
Next jj
Next j
Cells(1, 1).Value = a(1, 7)
Range("A1").Select
End Sub
Sub mondai2(ByVal x As Variant)
Sheets("Sheet2").Select
Cells(1, 1).Value = 0
Cells(2, 1).Value = 0
Range("A1").Select
Call saiki(1)
End Sub
Sub saiki(ByVal n As Integer)
a(n, 1) = 1
While a(n, 1) <= 7
If onaji(n) = 0 Then
If n < 7 Then
Call saiki(n + 1)
Else
Call check(1)
End If
End If
a(n, 1) = a(n, 1) + 1
Wend
End Sub
Sub check(ByVal x As Variant)
Dim j As Integer
Dim jj As Integer
For j = 2 To 7
For jj = 1 To 7 - (j - 1)
a(jj, j) = a(jj, j - 1) + a(jj + 1, j - 1)
Next jj
Next j
If Cells(1, 1).Value <= a(1, 7) Then
If Cells(1, 1).Value < a(1, 7) Then
Cells(1, 1).Value = a(1, 7)
Cells(2, 1).Value = 1
Columns("B:H").Select
Selection.ClearContents
Range("A1").Select
Else
Cells(2, 1).Value = Cells(2, 1).Value + 1
End If
For j = 1 To 7
Cells(Cells(2, 1).Value, j + 1).Value = a(j, 1)
Next j
End If
End Sub
Private Function onaji(ByVal n As Integer) As Integer
Dim j As Integer
onaji = 0
j = 1
While onaji = 0 And j < n
If a(j, 1) = a(n, 1) Then
onaji = 1
Else
j = j + 1
End If
Wend
End Function
解答・その2
(ペンネ−ム:スモークマン)
問1
これは単に計算するだけですね...
256
問2
明らかに...大きい数が真ん中にあれば繰り返したされるので...
1,3,5,7,6,4,2
1,3,6,7,5,4,2
1,4,5,7,6,3,2
1,4,6,7,5,3,2
で...350 がMax♪
でいいのかな...^^
解答・その5
(ペンネ−ム:やなせ)
最上階までに足される数字の個数
端の場合
1個 1個 0個 1個 0個 0個 1個 0個 0個 0個 1個 0個 0個 0個 0個 1個 0個 0個 0個 0個 0個 1個 0個 0個 0個 0個 0個 0個
2番目の場合
6個 5個 1個 4個 1個 0個 3個 1個 0個 0個 2個 1個 0個 0個 0個 1個 1個 0個 0個 0個 0個 0個 1個 0個 0個 0個 0個 0個
3番目の場合
15個 10個 5個 6個 4個 1個 3個 3個 1個 0個 1個 2個 1個 0個 0個 0個 1個 1個 0個 0個 0個 0個 0個 1個 0個 0個 0個 0個
真ん中の場合
20個 10個 10個 4個 6個 4個 1個 3個 3個 1個 0個 1個 2個 1個 0個 0個 0個 1個 1個 0個 0個 0個 0個 0個 1個 0個 0個 0個
足される回数は上の図のようになります。
問い1
最上階の数を求める式は
1×1+2×6+3×15+4×20+5×15+6×6+7×1=256
答え 256
さらに同図から中の方に大きな数字を持ってくると合計が多くなるので
問い2の答えは
両端は1と2。 端から2番目は3と4。 さらに3番目は5と6。 中央は7です。
ちなみに最上階の数は
1×1+3×6+5×15+7×20+6×15+4×6+2×1=350
解答・その6
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
一段目の1,2,3,4,5,6,7、を置き換えて
一段目をA,B,C,D,E,F,G、とすると
二段目はA+B,B+C,C+D,D+E,E+F,F+Gの6個の数字となります。
三段目はA+2B+C,B+2C+D,C+2D+E,D+2E+F,E+2F+Gの5個の数字となります。
四段目はA+3B+3C+D、B+3C+3D+E,C+3D+3E+F,D+3E+3F+G,の4個の数字となります。
五段目はA+4B+6C+4D+E、B+4C+6D+4E+F,C+4D+6E+4F+G、の3個の数字になります。
六段目はA+5B+10C+10D+5E+F、B+5C+10D+10E+5F+G,の2個の数字になります。
七段目はA+6B+15C+20D+15E+6F+G、の数字になります。
この数式のA〜Gまでに1〜7を当てはめると
1+(6×2)+(15×3)+(20×4)+(15×5)+(6×6)+7=256
一番上の数字を大きくするには倍数の大きい20倍のDを7として次に大きい15倍のC,Eに6又は5を入れて、次に大きい6倍数のB,Fに4又は3を入れて、最後のA,Bに2と1を並べます。
例として次のように並べて計算すると
1357642→1+18+75+140+90+24+2=350となります。
解答・その18
(ペンネ−ム:teki)
問1. 256
問2. 23=8通りの解答がありますが、一例を示します。
1,3,5,7,6,4,2
(1と2、3と4、5と6は入れ替え可能)
中央に最大数の7を入れ、これを取り巻くように大きい数から順に外側に向かって入れていけば完成します。
この場合の7段目の数は、いずれも350となります。
<解法>
算数で言えば、「パスカルの三角形」、数学で言えば2項定理ですね。
各数が7段目までに何回足されるかを考えます。
パスカルの三角形を利用すれば、
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1
で、問1は、1×1+6×2+15×3+20×4+15×5+6×6+1×7=256
問2は、最大数を中央に持ってくればいいことが、一目瞭然です。
解答・その7
(ペンネ−ム:巷の夢)
今、左から右への順番を1〜7とする。これらの順番を隣り合う2つの順番を加え、逆ピラミッドの数を記述してみると、
(1) (2) (3) (4) (5) (6) (7)
(1)+(2) (2)+(3) (3)+(4) (4)+(5) (5)+(6) (6)+(7)
(1)+2×(2)+3 (2)+2×(3)+(4) ・・・・・・・・・・・・・・・・・・・・・
(1)+3×(2)+3×(3)+(4) ・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・
(1)+6×(2)+15×(3)+20×(4)+15×(5)+6×(6)+(7)
となる。
これより問1.
(1)=1、(2)=2、・・・・・・、(7)=7を式(1)+6×(2)+15×(3)+20×(4)+15×(5)+6×(6)+(7)に代入して、256を得る。
問2.
式(1)+6×(2)+15×(3)+20×(4)+15×(5)+6×(6)+(7)を最大にするには、
(4)=7、(3)=5、(5)=6、(2)=3、(6)=4、(1)=1、(7)=2を代入すれば良い。
この合計は350となる。ところで、(3)と(5)、(2)と(6)、(1)と(7)は入れ替えても良いので組み合わせは8通りとなる。
因って求めるものは、
1365742、1375642、1465732、1475632、2365741、2375641、2465731及び2475631
である。
解答・その8
(ペンネ−ム:マオ)
1段目の数字を、左から順にa,b,c,d,e,f,gとする。
規則に従って、2段目は左から順に
a+b,b+c,c+d,d+e,e+f,f+g
3段目も同様にして
a+2b+c,b+2c+d,c+2d+e,d+2e+f,e+2f+g
となり、続けていくと、7段目は
a+6b+15c+20d+15e+6f+g … (※)
となる。
問1.256
(※)より、
1+12+45+80+75+36+7=256
問2.
(※)より、
1段目の左から4番目に最大の数値を、3,5番目に次に大きい数値を、
2,6番目に次に大きい数値をおけば、7段目の数値が最大になる。
よって、1段目の左から順に次のように並べればよい。
1番目…1(または2)
2番目…3(または4)
3番目…5(または6)
4番目…7
5番目…6(または5)
6番目…4(または3)
7番目…2(または1)
解答・その15
(ペンネ−ム:namiusagi)
問い1の答 256
問い2の答 左から2,4,6,7,5,3,1又は1,3,5,7,6,4,2 最大数 350
考え方
最下段(一段目)を左からa,b,c,d,e,f,gとし、題意に添って二段目を表すと左から
a+b,b+c,c+d,d+e,e+f,f+g
となり、三段目は左から
a+2b+c,b+2c+d,c+2d+e,d+2e+f,e+2f+g
同様に七段目を表すと、
a+6b+15c+20d+15e+6f+g
となる。係数の一番大きいのがdだから7を入れ、次に大きいc,eには6,5 又は5,6を入れ、
三番目に大きいb,fには4,3または3,4を入れ、いちばんちいさいa,gには2,1又は1,2を入れる。
解答・その16
(ペンネ−ム:falcon@中学教師)
問1
256
問2
真ん中を7にしてその両隣から、5と6、3と4、2と1を組にして左右に配置していく。
(ちなみに七段目は350)
<考え方>
問1
素直に足していって出す、というのが1つ。
あとは、一段目を左からa, b, c, d, e, f, g と置き、七段目を求めると
a + 6b + 15c + 20d + 15e + 6f + gとなるので、
それぞれ文字に1, 2, 3, 4, 5, 6, 7 を代入して計算する手が1つ。
問2
問1後半の考え方で出た七段目の形・係数を見て判断。
<補足>
頂点の形の文字の係数は結局二項定理やパスカルの三角形を用いて出すことができる。
一段目の数のそれぞれが、どう枝分かれして頂点の位置に達するかを考えればなるほどである。
解答・その21
(ペンネ−ム:夜ふかしのつらいおじさん)
問題を少し変えて答えます。
2数の和を上に積み重ねるより、下に下ろしていく方が自然なので上下を反対にして答えます。
次のようにパスカルの三角形と逆さまのピラミッドを用意します。
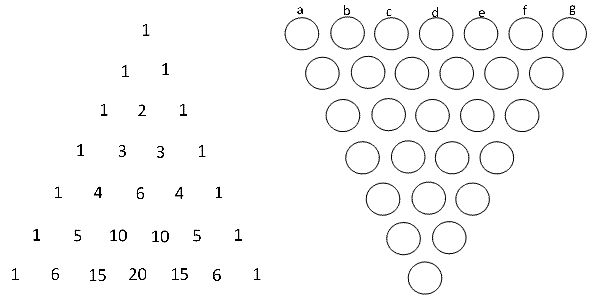
逆さピラミッドの位置を上からの段数と左からの順番の2組の数で表すことにします。
例えば、上から3段目で左から2番目の位置を(3,2)とします。
だから一番下は、(7,1)です。
仕組みになれるために、例としてcの位置にある数は下に進むと何回足されるかを考えます。
bと足す場合と、dと足す場合の2回で、2段目の(2,2)と(2,3)の位置に現れます。
3段目は、(2,1)と(2,2)、(2,2)と(2,3)、(2,3)と(2,4)を足すので、(3,1)、(3,2)、(3,3)の位置に現れます。
注意するのは、(3,2)には、(2,2)と(2,3)にcが含まれていたので、2個分になるということです。
パスカルの三角形の頂点の「1」が逆さピラミッドのcの位置に重なるように置くと様子が分かりやすくなります。
このように、7段目まででcの位置にある数は15回足されることが分かります。
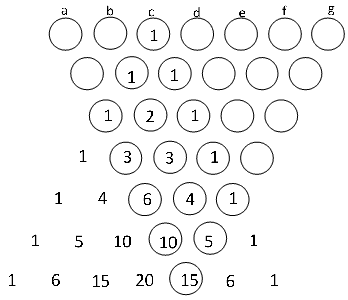
このように考えると、
aの位置は、 1回
bの位置は、 6回
cの位置は、 15回
dの位置は、 20回
eの位置は、 15回
fの位置は、 6回
gの位置は、 1回
足されます。
問1
1×1+6×2+15×3+20×4+15×5+6×6+1×7=256
問2
中央が20回、その両隣が15回、さらにその外が6回、両端が1回足されるので、
「1357642」、「1367542」、「1457632」、「1467532」(それぞれの逆順も)
のように配置すれば良いことになります。
この場合、合計は350のようです。
また、1と7、2と6、3と5を入れ替えると我が小さくなります。
この場合、合計は162のようです。
おまけに、(350+162)/2=256です。
解答・その9
(ペンネ−ム:オヤジ)
一段目の左から順に,A,B,C,D,E,F,G とすると七段目の数は、
A+6B+15C+20D+15E+6F+G
となる
問1
従って A=1,B=2,C=3,D=4,E=5,F=6,G=7 を代入すると
∴256
問2
七段目の数を最大にするには AまたはG=1または2,BまたはF=3または4,
CまたはE=5または6,D=7のとき最大値 350 最大にする数の並びは,8通り
すなわち
(A,B,C,D,E,F,G) =(1,3,5,7,6,4,2) =(1,3,6,7,5,4,2) =(1,4,5,7,6,3,2) =(1,4,6,7,5,3,2) =(2,3,5,7,6,4,1) =(2,3,6,7,5,4,1) =(2,4,5,7,6,3,1) =(2,4,6,7,5,3,1)∴ 最大値 350 ,一段目の数は,上記 8通り
解答・その22
(ペンネ−ム:再出発)
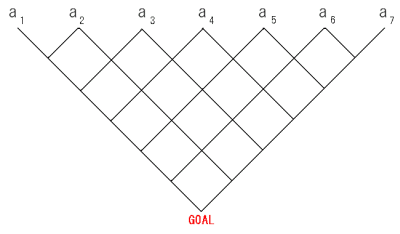
図は逆三角形に描きましたが、7段目の和は
a1,a2,a3,...,a7
がそれぞれGOAL目指して最短で行く道筋の数が
それぞれの係数になっています。
従って七段目の和は
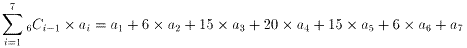
したがって
問1の答は
256
問2の答は
aiを用いて表すと、
(a1,a7)=(1,2),(2,1)
(a2,a6)=(3,4),(4,3)
(a3,a5)=(5,6),(6,5)
a4=7
解答・その3
(ペンネ−ム:迷子の雄猫)
問1
(256) 七段目 (112)(144) 六段目 (48)(64)(80) 五段目 (20)(28)(36)(44) 四段目 (8)(12)(16)(20)(24) 三段目 (3)(5)(7)(9)(11)(13) 二段目 (1)(2)(3)(4)(5)(6)(7) 一段目
問2
それぞれの括弧の中の数字を1増やすと、
一番上の段の数字がいくつ増えるかを計算すると、
以下のようになる。
(1) (1)(1) (1)(2)(1) (1)(3)(3)(1) (1)(4)(6)(4)(1) (1)(5)(10)(10)(5)(1) (1)(6)(15)(20)(15)(6)(1)
よって、七段のピラミッドの一番上の( )の中の数を最大にするためには、
一段目の7つの( )に1〜7を以下の通りに入れるとよい。
(4)に7
(3)、(5)に6,5(順不同)
(2)、(6)に4,3(順不同)
(1)、(7)に2,1(順不同)
解答・その11
(ペンネ−ム:T_Tatekawa)
問1
一段目の各々のカッコから,七段目の?まで右上,左上に進んで
到達する道順が何通りかを数えます.
1,7:1通り
2,6:6通り
3,5:15通り
4:20通り
この通りの回数だけ,たし算では?のところに上がるまで各々の数を
足し上げています.
よって,
4 x 20 + (3+5) x 15 + (2+6) x 6 + (1+7) x 1 = 80 + 120 + 48 + 8 = 256
問2
問1の考え方を元にすると,七段目の?を最大にするには,一段目の
内側に大きな数を置けば良い.
例えば
(1) (3) (5) (7) (6) (4) (2)
(1, 2), (3, 4), (5, 6) の左右は逆でも良い.
この場合の七段目の数は
7 x 20 + (5+6) x 15 + (3+4) x 6 + (1+2) x 1 = 140 + 165 + 42 + 3 = 350
解答・その14
(ペンネ−ム:superyamachan)
問1 256
問2 一段目の数列を{an}、二段目を{bn}、三段目を{cn}…とする
と、七段目はgとおける。
この問題の定義より、bk=ak+ak+1、ck=ck+ck+1、…、g=f1+f2
よって、
g=e1+e2+e2+e3
=e1+2e2+e3
=d1+d2+2(d2+d3)+d3+d4
=d1+3d2+3d3+d4
=c1+c2+3(c2+c3)+3(c3+c4)+c4+c5
=c1+4c2+6c3+4c4+c5
・・・・・・・・・・・
=b1+5b2+10b3+10b4+5b5+b6
=a1+6a2+15a3+20a4+15a5+6a6+a7
係数の違いから、a4>(a3,a5)>(a2,a6)>(a1,a7)が成り立つとき、gが最大となる。
よって、a4=7、(a3,a)=(5,6)、(6,5)、(a2,a6)=(3,4)、(4,3)、(a1,a7)=(1,2)、(2,1)
ゆえに、(1,3,5,7,6,4,2)(2,3,5,7,6,4,1)
(1,4,5,7,6,3,2)(2,4,5,7,6,3,1)
(1,3,6,7,5,4,2)(2,3,6,7,5,4,1)
(1,4,6,7,5,3,2)(2,4,6,7,5,3,1)
いずれの場合もg=20×7+15×(5+6)+6×(3+4)+(1+2)=140+165+42+3=350
解答・その10
(ペンネ−ム:のっこん)
一段目を左から順に a,b,c,d,e,f,g とすると
二段目は 〃 a+b,b+c,c+d,d+e,e+f,f+g となり
三段目は 〃 a+2b+c,b+2c+d,c+2d+e,d+2e+f,e+2f+g となり
四段目は 〃 a+3b+3c+d,b+3c+3d+e,c+3d+3e+f,d+3e+3f+g となり
五段目は 〃 a+4b+6c+4d+e,b+4c+6d+4e+f,c+4d+6e+4f+g となり
六段目は 〃 a+5b+10c+10d+5e+f,b+5c+10d+10e+5f+g となり
七段目は a+6b+15c+20d+15e+6f+g となる
問1
1+6・2+15・3+20・4+15・5+6・6+7=256
問2
七段目の数を最大にするには
d=7
(c,e)=(5,6) 逆も可
(b,f)=(3,4) 〃
(a,g)=(1,2) 〃 とすればよい
解答・その23
(ペンネ−ム:三角定規)
<図1>において,A,B,C,D,E,F,G から T に至る最短経路の数は,
6C0,6C1,6C2,6C3,
6C4,6C5,6C6 で,題意のように数の和を積み上げるとき,T での和に数 A,B,…,はこ
の回数だけ反映される。よって,
T=A+6B+15C+20D+15E+6F+G
(1) 題意より,T=1+6・2+15・3+20・4+15・5+6・6+7=256 …[答]<図2>
(2) T を最大にするには,係数が大きいところに大きな数を入れればよいので,
T=1+6・3+15・5+20・7+15・6+6・4+2=350 …[答]<図3>
解答・その12
(ペンネ−ム:SOU)
問2 一段目の各々の変数を端から順に A1,A2,A3,A4,A5,A6,A7 とすると、七段目は 20A4+15(A3+A5)+6(A2+A6)+(A1+A7) ・・・☆ となるので、係数による倍率を考えると 20*7+15(5+6)+6(3+4)+(1+2) の時が最も値が大きく、350となる // 問1 ☆で An=n とすればよく、 256 //
解答・その13
(ペンネ−ム:バルタン星人)
問い1:256
問い2:1,3,5,7,6,4,2(逆順でもよし)
考え方:n段積みの時、最下段の各項は、
(A+B)n−1の係数だけ足されることになる。
7段なら、6乗の係数、各1,6,15,20,15,6,1回
足されることになるので
(1+7)×1+(2+6)×6+(3+5)×15+4×20
=8×(1+6+15+10)
=8×32
=256
最大にするには両端から小さな数をはめ、中央を最大の数に
すればよい。この時
(1+2)×1+(3+4)×6+(5+6)×15+7×20
=350が最大となる。
解答・その20
(ペンネ−ム:シュレーディンガーの三毛猫)
1段目の数が最上段へどのように寄与するかを、最上段へ至る道筋の場合の数を用いて考察する。
例えば、2段のピラミッドにおいて1段目に左から自然数a,bをおくと、
1段目の和はa+b。最上段である2段目の数もa+bとなって両者は等しくなる。
これを、1段目から2段目に至る道筋がそれぞれ一通り(aは右上へ、bは左上へ)なので、
1段目の数が2段目に登る時に、それぞれ1回ずつ足されるからであると考える。
すると、3段のピラミッドにおいて1段目に左から自然数a,b,cをおいたとき、
1段目の和がa+b+cなのに対し、2段目の和は(a+b)+(b+c)となり1段目の和よりbだけ大きくなることは、
2段目に登る時の道筋が、両端のa,cはそれぞれ右上、左上の一通りであるのに対し、
bは右上と左上の二通りあり、2段目へ2回足されるからである、と考えることができる。
なお、2段目の2数が3段目に登る時の道筋は右上ないし左上の一本ずつなので、
最上段である3段目の数と、2段目の2数の和は等しくなる。
すなわち、
一段上に上る時の道筋が一通りなら1回、二通りなら2回それぞれの数が一段上に足されるというルールと、
最上段へ登る過程で道筋が二通りあるということは、1段目から最上段へ登る道筋が一通り増えるという事実から、
本問は、
「一段目のある位置から最上段に登る場合の数とその位置の数との積の、
一段目のすべての位置についてとった総和が最上段の数に等しい」
と言い換えることができる。
(問1)
7段のピラミッドにおいて、1段目に左から自然数a,b,c,d,e,f,gをおく。
1段目から7段目まで登る道筋の場合の数は、右上または左上に移動する動作を
6回繰り返す組み合わせの数となり、1段目の左から何番目の位置かによって一様に決まる。
1段目の一番左の位置を0、右隣を1、というように番号付けして一番右の位置を6とすると、
6Ci (i=0,1,2,3,4,5,6)
と表式でき、1段目から7段目まで登る場合の数は左から(1、6、15、20、15、6、1)と求まる。
これらとその位置の数との積の総和が7段目の数となるので、1段目の数(a~g)と7段目の数との関係として
(7段目の数)=1×(a+g)+6×(b+f)+15×(c+e)+20×d ・・・(1)
を得る。
与えられた数は(a,b,c,d,e,f,g)=(1,2,3,4,5,6,7)なので、これを(1)に代入して
256を解として得る。
(問2)
7段目の数を最大にするためには、(1)の係数に着目して、
d=7, (c,e)=(5,6), (b,f)=(3,4), (a,g)=(1,2) ・・・(2)
とおけば良く、このとき、最大値350を得る。
なお、(2)のうち、(c,e)、(b,f)、(a,g)に入る数は
(1)の対称性により入れ換えても良く、最大値を与える1段目の数はそれぞれ
(a,b,c,d,e,f,g)=(1,4,5,7,6,3,2)
(a,b,c,d,e,f,g)=(2,4,5,7,6,3,1)
(a,b,c,d,e,f,g)=(1,3,5,7,6,4,2)
(a,b,c,d,e,f,g)=(2,3,5,7,6,4,1)
(a,b,c,d,e,f,g)=(1,4,6,7,5,3,2)
(a,b,c,d,e,f,g)=(2,4,6,7,5,3,1)
(a,b,c,d,e,f,g)=(1,3,6,7,5,4,2)
(a,b,c,d,e,f,g)=(2,3,6,7,5,4,1)
の8通り存在する。
解答・その4
(ペンネ−ム:haya)
問1: 256
問2: 左から、1, 3, 5, 7, 6, 4, 2 のように中央に大きな数字が来るように配置すればよい。
左右対称なので 23 個の同値の解があり、ピラミッドの頂上は何れも 350 となる。
350
170 180
77 93 87
32 45 48 39
12 20 25 23 16
4 8 12 13 10 6
1 3 5 7 6 4 2
【解き方】
問1: ひたすら足し算する。
問2: 下の段の数値がピラミッドの頂上に到達するまでに何重に計算されるかは、インドの紀元前の文献またはイタリア人の言うタルタリアの三角形で示される二項係数の如くなるので解を得る。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
解答・その19
(ペンネ−ム:長崎島原かがみ)
問1 【答】256
問2 一段目の数を左から a、b、c、d、e、f、g とおくと、
七段目の数は a+6b+15c+20d+15e+6f+g となる。(下記参照)
したがって、七段目の数を最大にするためには、係数の大きい方から順に
7〜1と入れていけばよい。すなわち、
d=7
(c、e)=(5,6)または(6,5)
(b、f)=(3,4)または(4,3)
(a、g)=(1,2)または(2,1)
このとき、最大値は350になる。
【答】 d=7
(c、e)=(5,6)または(6,5)
(b、f)=(3,4)または(4,3)
(a、g)=(1,2)または(2,1)
最大値 350
結局、この数列は二項係数みたいになるんですね。
7段目は(x+y)6 の係数 1、6、15、20、15、6、1 が出てきます。
ちなみに、全ての段を左詰めで書いていくと、下記のようになります。
7段目 a+6b+15c+20d+15e+6f+g 6段目 a+5b+10c+10d+5e+f b+5c+10d+10e+5f+g 5段目 a+4b+6c+4d+e b+4c+6d+4e+f c+4d+6e+4f+g 4段目 a+3b+3c+d b+3c+3d+e c+3d+3e+f d+3e+3f+g 3段目 a+2b+c b+2c+d c+2d+e d+2e+f e+2f+g 2段目 a+b b+c c+d d+e e+f f+g 1段目 a b c d e f g
解答・その17
(ペンネ−ム:転位反応)
1段目の数字をa,b,c,・・・gとし、題意に沿って足し算を行い、整理すると以下の通り。
| 1段目 | 2段目 | 3段目 | 4段目 | 5段目 | 6段目 | 7段目 |
|---|---|---|---|---|---|---|
| a | ||||||
| a+b | ||||||
| b | a+2b+c | |||||
| b+c | a+3b+3c+d | |||||
| c | b+2c+d | a+4b+6c+4d+e | ||||
| c+d | b+3c+3d+e | a+5b+10c+10d+5e+f | ||||
| d | c+2d+e | b+4c+6d+4e+f | a+6b+15c+20d+15e+6f+g | |||
| d+e | c+3d+3e+f | b+5c+10d+10e+5f+g | ||||
| e | d+2e+f | c+4d+6e+4f+g | ||||
| e+f | d+3e+3f+g | |||||
| f | e+2f+g | |||||
| f+g | ||||||
| g |
7段目は、a+6b+15c+20d+15e+6f+g なので
問1:
1+6×2+15×3+20×4+15×5+6×6+7=256
問2:
7段目の数を最大にするには、下表に沿って1〜7の数字を重複しないように( )に入れれば良い。
このとき、7段目の数は350
| a | 1 or 2 |
|---|---|
| b | 3 or 4 |
| c | 5 or 6 |
| d | 7 |
| e | 5 or 6 |
| f | 3 or 4 |
| g | 1 or 2 |
正解者
| 夜ふかしのつらいおじさん | teki | namiusagi |
| falcon@中学教師 | 浜田 明巳 | 巷の夢 |
| オヤジ | のっこん | 再出発 |
| 長崎島原かがみ | superyamachan | スモークマン |
| 転位反応 | やなせ | 迷子の雄猫 |
| SOU | haya | 杖のおじさん |
| T_Tatekawa | シュレーディンガーの三毛猫 | マオ |
| 三角定規 | バルタン星人 |
コメント
一段目の数を左から a、b、c、d、e、f、g とおくと、
七段目の数は
a+6b+15c+20d+15e+6f+g
となります。
それぞれの場所を出発して7段目に到達するまでの道順の数を合計しているということになりますが、
二項係数がこんなところにも現れてくるのは、不思議といえば不思議、当然といえば当然ですね。
 top
top