栤戣157丂2010擭偺栤戣
師偺幃偺俙丄俛丄俠丄俢偼偦傟偧傟偺偗偨偺悢帤傪昞偟丄
摨偠暥帤偼摨偠悢帤傪昞偟傑偡丅
丂丂丂俙俛俠俢亅俙俛俠亅俙俛亅俙亖俀侽侾侽
係偗偨偺惍悢俙俛俠俢傪媮傔偰偔偩偝偄丅
栤戣偺弌揟
嶼悢僆儕儞僺僢僋偵挧愴
嶼悢僆儕儞僺僢僋埾堳夛曇
島択幮僽儖乕僶僢僋僗
2004擭僩儔僀傾儖栤戣丂夵戣
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗昹揷丂柧枻乯
捠忢暍柺嶼偱偼丆堎側傞暥帤偵偼堎側傞悢抣傪擖傟傞偺偱偡偑丆偦傟偩偲媮傔傜傟傑偣傫偱偟偨偺偱丆
偦偺忦審傪庢傝暐偄夝偄偰傒傑偟偨.
摎偼2259丆2260偺俀屄偱偡丏僄僋僙儖偺儅僋儘偱偡丏
Option Explicit
'ABCD-ABC-AB-A=2010
'仺 2010
' A
' AB
'+ ABC
'-------
' ABCD
Sub Macro1() 'A乣D偑屳偄偵堎側傞応崌
Sheets("Sheet1").Select
Cells(1, 1).Value = 0 '夝偺屄悢
Dim A As Integer
Dim B As Integer
Dim C As Integer
Dim D As Integer
Dim kuriagari(3) As Integer
Dim gyou As Integer
For A = 1 To 9
For B = 0 To 9
If A <> B Then
For C = 0 To 9
If A <> C And B <> C Then
D = (0 + A + B + C) Mod 10
If A <> D And B <> D And C <> D Then
kuriagari(1) = (0 + A + B + C) \ 10
If (1 + A + B + kuriagari(1)) Mod 10 = C Then
kuriagari(2) = (1 + A + B + kuriagari(1)) \ 10
If (0 + A + kuriagari(2)) Mod 10 = B Then
kuriagari(3) = (0 + A + kuriagari(2)) \ 10
If 2 + kuriagari(3) = A Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
gyou = Cells(1, 1).Value * 6 - 5
Cells(gyou, 2).Value = A * 1000 + B * 100 + C * 10 + D
Cells(gyou + 1, 2).Value = -(A * 100 + B * 10 + C)
Cells(gyou + 2, 2).Value = -(A * 10 + B)
Cells(gyou + 3, 2).Value = -A
Cells(gyou + 4, 2).Value = 2010
End If
End If
End If
End If
End If
Next C
End If
Next B
Next A
End Sub
Sub Macro2()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0 '夝偺屄悢
Dim A As Integer
Dim B As Integer
Dim C As Integer
Dim D As Integer
Dim kuriagari(3) As Integer
Dim gyou As Integer
For A = 1 To 9
For B = 0 To 9
For C = 0 To 9
D = (0 + A + B + C) Mod 10
kuriagari(1) = (0 + A + B + C) \ 10
If (1 + A + B + kuriagari(1)) Mod 10 = C Then
kuriagari(2) = (1 + A + B + kuriagari(1)) \ 10
If (0 + A + kuriagari(2)) Mod 10 = B Then
kuriagari(3) = (0 + A + kuriagari(2)) \ 10
If 2 + kuriagari(3) = A Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
gyou = Cells(1, 1).Value * 6 - 5
Cells(gyou, 2).Value = A * 1000 + B * 100 + C * 10 + D
Cells(gyou + 1, 2).Value = -(A * 100 + B * 10 + C)
Cells(gyou + 2, 2).Value = -(A * 10 + B)
Cells(gyou + 3, 2).Value = -A
Cells(gyou + 4, 2).Value = 2010
End If
End If
End If
Next C
Next B
Next A
End Sub
夝摎丒偦偺2
乮儁儞僱亅儉丗Yama偪傖傫乯
梌偊傜傟偨摍幃偼師偺幃偲摨抣偱偡丅
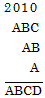
偟偨偑偭偰丄A=2丄B=A=2丄C=1+A+B=1+2+2=5丄
D亖A亄B+C=2+2+5=9丏
栤戣偺忦審偵偼乽摨偠暥帤偼摨偠悢帤乿偩偗側偺偱丄傕偟A=B傪嫋梕偡傟偽丄
摎偊 2259-225-22-2=2010
偟偐偟丄乽堎側傞暥帤偼堎側傞悢帤乿偩偲偡傞偲丄偙偺偲偒偼夝側偟丅
夝摎丒偦偺3
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂俙俛俠俢亖俀俀俆俋丂枖偼丂俙俛俠俢亖俀俀俇侽丂偺俀偮偱偡丅
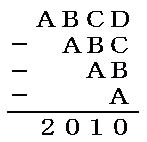
俙亖俀丂俛亖俙
俠亖俙亄俛亄侾亖俆丂枖偼丂俠亖俙亄俛亄俀亖俇丂偺俀捠傝偁傝傑偡丅
侾偺埵偑侽偵側傞俢傪媮傔傑偡丅
俠亖俆丂偺帪丂俢乗俀乗俀乗俆亖侽丂丂俢亖俋偱偡丅
俠亖俇丂偺帪丂俢乗俀乗俀乗俇亖侽丂丂俢亖侾侽側偺偱侾埵偐傜堷偗傑偣傫偺偱侾侽偺埵偺俠偐傜侾傪堷偒傑偡丅偦偆偡傞偲俠亖俇亅侾亖俆丂偲側傝丂侾埵偼侾侽亅侾侽亖侽偲側傝丂俢亖侽偲寛掕偝傟傑偡丅
夝摎丒偦偺4
乮儁儞僱亅儉丗teki乯
亙夝摎亜丂丂俀俀俆俋偲俀俀俇侽
- 奺寘偵孞傝壓偑傝偑惗偠偰偄側偄偲壖掕偡傞偲丄
丂俙亖俀
丂俛亖俙
丂俠亖俙亄俛亄侾
丂俢亖俙亄俛亄俠
偙傟傪夝偄偰丄乮俙丆俛丆俠丆俢乯亖乮俀丆俀丆俆丆俋乯
- 廫偺埵偵孞傝壓偑傝偑偁傞偲壖掕偡傞偲丄
丂俙亖俀
丂俛亖俙
丂俠亖俙亄俛亄俀
丂俢亖俙亄俛亄俠亅侾侽
偙傟傪夝偄偰丂乮俙丆俛丆俠丆俢乯亖乮俀丆俀丆俇丆侽乯
- 昐偺埵偵孞傝壓偑傝偑偁傞偲壖掕偡傞偲丄
丂俙亖俀
丂俛亖俙亄侾
丂俠亖俙亄俛亅俋
傛偭偰夝側偟丅
- 嵟忋埵偵孞傝壓偑傝偑偁傞偲壖掕偡傞偲丄
丂俙亖俁
丂俛亖俙亅侾侽
傛偭偰夝側偟丅
- 嵟忋埵媦傃昐偺埵偵孞傝壓偑傝偑偁傞偲壖掕偡傞偲丄
丂俙亖俁
丂俛亖俙亅俋
傛偭偰夝側偟丅
夝摎丒偦偺5
乮儁儞僱亅儉丗岼偺柌乯
戣堄傛傝A亖2側偄偟3偱偁傞偙偲偑暘偐傞丅偙傟傛傝B亞A偱偁傞丅
偦偙偱B=2偲偡傞偲丄C偼5側偄偟6偱偁傞丅
偦偙偱C亖5偲偡傞偲丄D亖A+B+C傛傝D=9偲側傞丅
偲偙傠偱丄C亖6偲偡傞偲丄D亖A+B+C傛傝D=0偲側傞丅
師偵B=3偲偡傞偲丄C亖0偲偄偆嵟彫悢偱傕堷偒嶼寁嶼偟偨寢壥偺10偺埵偼1偵偼側傜側偄丅
枖丄A亖3偲偡傞偲堷偒嶼寁嶼偟偨寢壥偺100偺埵偼0偵偼側傜側偄丅
埲忋偺偙偲偐傜媮傔傞4寘偺惍悢ABCD偼2259偲2260偱偁傞丅
夝摎丒偦偺6
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
ABCD-ABC-AB-A=2010
A(1000-100-10-1)+B(100-10-1)+C(10-1)+D=2010
D-A-B-C=0
C-A-B=1 or 2
B-A=0 or 1
A=2
2259
2260
236仏
237仏
屻幰2屄偼...偦傟傪枮偨偡 D >10 偼側偄偺偱...忋擇偮偑摎偊偱偄偄偺偐側丠
夝摎丒偦偺7
乮儁儞僱亅儉丗儅僆乯
夝摎丗2259丆2260
媮傔傞4寘偺惍悢ABCD偵偍偄偰丆
A,B,C,D伕Z , 1亝A亝9 , 0亝B,C,D亝9
忦審傛傝
丂丂(1000A+100B+10C+D)-(100A+10B+C)-(10A+B)-A=2010
曄宍偟偰
丂丂889A+89B+9C+D=2010
A=1偺偲偒
丂丂889+89B+9C+D=2010 傛傝
丂丂偙傟傪枮偨偡B丆C丆D偺抣偼懚嵼偟側偄丅
丂丂A亞3偺偲偒傕摨條丅傛偭偰A=2
A=2偺偲偒
丂丂1778+89B+9C+D=2010
丂丂89B+9C+D= 232
丂丂B=1偺偲偒
丂丂丂89+9C+D=232 傛傝
丂丂丂偙傟傪枮偨偡C丆D偺抣偼懚嵼偟側偄丅
丂丂丂B亞3偺偲偒傕摨條丅傛偭偰B=2
丂丂B=2偺偲偒
丂丂丂178+9C+D=232
丂丂丂9C+D=54
丂丂丂偙傟傪枮偨偡偺偼C=6,D=0 傑偨偼 C=5,D=9
偙傟傛傝
丂丂A=2,B=2,C=6,D=0 傑偨偼 A=2,B=2,C=5,D=9
傛偭偰 2260偲2259丅
夝摎丒偦偺8
乮儁儞僱亅儉丗俼倄倀1128乯
幃傪惍棟偡傞偲
丂丂丂俉俉俋俙亄俉俋俛亄俋俠亄俢亖俀侽侾侽亖2000+000+10+0
奺崁偵懳墳偝偣偰
丂丂丂2000亅889俙亖侽
俙亖俀丂偁傑傝222
丂丂丂222+0-89俛亖0
俛亖2丂偁傑傝44
丂丂丂0+44-9俠亖0
俠亖俇丂偁傑傝0
丂丂丂俢亖0
屘偵俙俛俠俢亖俀俀俇侽
偨偩偟俠亖俆丂偁傑傝9
俢亖俋
俙俛俠俢亖俀俀俆俋
偲偄偆夝傕偁傝丄偙偺晄掕曽掱幃偵偼俀捠傝偺夝偑偁傞丅
偳偪傜傕惓夝偲巚偆偑戞堦偺夝偺曽偑忚梋偺奣擮偐傜偡傞偲僗儅乕僩偲巚偆丅
彯丄悢妛偼姰慡側尩枾惈傪曐偮偙偲偵傛傞旤傪捛媮偡傞妛栤偱偁傞偙偲偐傜丄僗儅乕
僩偝偩偗偱偼堄枴傪帩偨側偄丅偟偨偑偭偰擇捠傝偺夝傪帩偭偰惓夝偲偡傞偺偑惓偟偄
偲偄偆偺偑寢榑丅
偙偺庬偺栤戣偵偼傛傝堦斒惈傪帩偨偣偨傾儖僑儕僘儉偑偁傞傛偆偵婰壇偡傞偑傕偆僕
僕僀側偺偱朰傟偰偟傑偭偨丒丒丒丒丅
乮戣堄偐傜俙偼1偐傜俋傑偱偺惍悢俛丆俠丆俢偼0偐傜9傑偱偺惍悢偲彑庤偵夝庍偟傑
偟偨丅奺乆1暥帤偲偼彂偄偰偼偄傑偣傫偱偟偨偑乯
夝摎丒偦偺9
乮儁儞僱亅儉丗namiusagi乯
丂丂丂(1000-100-10-1)A-(100-10-1)B-(10-1)C-D=889A+89B+9C+D=2010
側偺偱丄A偵2傪偄傟偰乮1偩偲B偑2寘偵側偭偰偟傑偆偺偱晄壜乯丄
丂丂丂1778+89B+9C+D=2010偱丄89B+9C+D=232.
偙傟偵B偵2傪擖傟偰丄
丂丂丂178+9C+D=232偱丄9C+D=54.
偙傟偵C偵6傪擖傟傟偽D偼0偱丄5傪擖傟傟偽9偵側傞丅
傛偭偰A=2,B=2,C=6,D=0枖偼A=2,B=2,C=5,D=9偱丄2260偍傛傃2059偑媮傔傞4寘偺惍悢偲側傞丅
夝摎丒偦偺10
乮儁儞僱亅儉丗falcon@拞妛嫵巘乯
亙摎偊亜
2260丂偲丂2259
亙峫偊曽亜
傑偢丄
丂丂俙俛俠俢亅俙俛俠亅俙俛亅俙亖2010
偲偄偆梌幃偺宍偐傜丄愮偺埵偵拝栚偡傞偲乽俙偼俀偐俁乿偲傢偐傞丅
師偵丄梌幃傪曄宍偟偰
丂丂889俙亄89俛亄9俠亄俢亖2010
偲偡傞偲丄俙亖3偼晄揔偲暘偐傝丄俙亖2偲寛傑傞丅
師偵俙亖2傪戙擖偟偰惍棟偡傞偲
丂丂89俛亄9俠亄俢亖232
偲偄偆幃偑偊傜傟丄俛偺壜擻惈偼0丆1丆2偲梕堈偵峣傜傟傞丅
戙擖偟偰妋偐傔傞偲丄俛亖0丆1偼晄揔偲暘偐傝丄俛亖2偲寛傑傞丅
偝傜偵俛亖2傪戙擖偟偰惍棟偡傞偲
丂丂9俠亄俢亖54
偲偄偆幃偑偊傜傟丄偙傟傪枮偨偡俠偲俢偺慻偼乮俠丆俢乯亖乮6丆0乯丆乮5丆9乯偺傒丅
偟偨偑偭偰丄梌幃傪枮偨偡係偗偨偺惍悢俙俛俠俢偼2260偲2259偱偁傞丅
夝摎丒偦偺11
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
丂俙俛俠俢亅俙俛俠亅俙俛亅俙
亖俙侽侽侽亄俛侽侽亄俠侽亄俢亅俙俙俙亅俛俛亅俠
亖俙亊乮侾侽侽侽亅侾侾侾乯亄俛亊乮侾侽侽亅侾侾乯亄俠亊乮侾侽亅侾乯亄俢
亖俉俉俋俙亄俉俋俛亄俋俠亄俢
偲曄宍偱偒傑偡丅
堦曽俀侽侾侽偼丄
丂俀侽侾侽
亖俉俉俋亊俀亄俀俁俀
亖俉俉俋亊俀亄俉俋亊俀亄俆係
亖俉俉俋亊俀亄俉俋亊俀亄俋亊俆亄俋
傑偨偼丄
亖俉俉俋亊俀亄俉俋亊俀亄俋亊俇亄侽
偲曄宍偱偒傞偺偱丄
俙亖俀丄俛亖俀丄俠亖俆丄俢亖俋
傑偨偼丄
俙亖俀丄俛亖俀丄俠亖俇丄俢亖侽偱偡丅
偙偺栤戣偼俙亖俛偲側偭偰偪傚偭偲惿偟偄婥偑偟傑偡丅
偁偲俁俇擭変枬偟偰丄俀侽係俇擭偩偲俙俛俠俢偑偡傋偰堎側傝傑偡丅
夝摎丒偦偺12
乮儁儞僱亅儉丗僆儎僕乯
媮傔傞丂係寘偺帺慠悢傪俙俛俠俢亖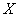 偲偡傞偲丄
梌幃偼丄壓婰偺條偵側傞
偲偡傞偲丄
梌幃偼丄壓婰偺條偵側傞
[丂]丗Gauss婰崋偲偡傞偲
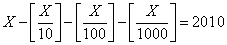 丒丒丒乮嘥乯
丒丒丒乮嘥乯
偙偙偱丄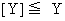 丂偲乮嘥乯傛傝
丂偲乮嘥乯傛傝
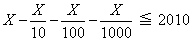
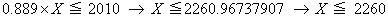
偙偙偱丂乮嘥乯幃偼丄扨挷旕尭彮乮扨挷憹壛偱偼側偄乯偱偁傞偐傜
亪丂俀俀俆俋丂偲俀俀俇侽
佹丂俀俀俇侽亅俀俀俇亅俀俀亅俀亖俀侽侾侽
丂丂俀俀俆俋亅俀俀俆亅俀俀亅俀亖俀侽侾侽
丂丂俀俀俆俉亅俀俀俆亅俀俀亅俀亖俀侽侽俋
夝摎丒偦偺13
乮儁儞僱亅儉丗嵞弌敪乯
乮夝乯
丂丂丂丂俀侽侾侽 丂丂丂亄丂俙俛俠 丂丂丂亄丂丂俙俛 丂丂丂亄丂丂丂俙 丂丂丂亅亅亅亅亅 丂丂丂丂俙俛俠俢
孞傝忋偑傝傪峫偊傞偲柧傜偐偵
丂丂俙亖俀
偙偺偲偒俛亖俀丄俁偱偡偑
俛亖俀偺偲偒偼惉傝棫偪傑偡偑丄
俛亖俁偺偲偒
俆亝俆亄俠亝侾係傛傝
丂丂侾亄俁亄俀亄乮俆亄俠乯亸侾侽亝俈
側偺偱
俙亖俛
偲側傝丄惉傝棫偪傑偣傫丅
偙偙傑偱偱
俙亖俛亖俀偲側傝
丂丂丂丂俀侽侾侽 丂丂丂亄丂俀俀俠 丂丂丂亄丂丂俀俀 丂丂丂亄丂丂丂俀 丂丂丂亅亅亅亅亅 丂丂丂丂俀俀俠俢
偙偙偱丄係亝係亄俠亝侾俁傛傝
丂丂俆亄乮係亄俠乯亸侾侽亖俠
偐傜丄
丂丂俠亖俆丄俇
丂丂俠亖俆偺偲偒俢亖俋
丂丂俠亖俇偺偲偒俢亖侽
偟偨偑偭偰媮傔傞係寘偺帺慠悢偼
丂丂丂俀俀俆俋丄俀俀俇侽丒丒丒(摎)
夝摎丒偦偺14
乮儁儞僱亅儉丗柪巕偺梇擫乯
俙俛俠俢亅俙俛俠亅俙俛亅俙亖俀侽侾侽
堏崁偟偰懌偟嶼偵偡傞偲丄
丂丂俙俛俠俢亖俀侽侾侽亄俙俛俠亄俙俛亄俙
俀侽侾侽偵俁寘偺悢傪壛偊傞偺偩偐傜摎偊偼係侽侽侽枹枮丅
傛偭偰俙偼俀偐俁丅
俀侽侾侽偵係侽侽枹枮偺悢傪壛偊傞偺偩偐傜摎偊偼俁侽侽侽枹枮丅
傛偭偰俙偼俀丅戙擖偟偰
丂丂俀俛俠俢亖俀侽侾侽亄俀俛俠亄俀俛亄俀
惍棟偟偰
丂丂俛俠俢亖俀俁俀亄俛俠亄俛
俀俁俀偵俀寘偺悢傪壛偊傞偺偩偐傜摎偊偼係侽侽枹枮丅
傛偭偰俛偼俀偐俁丅
俀俁俀偵係侽枹枮偺悢傪壛偊傞偺偩偐傜摎偊偼俁侽侽枹枮丅
傛偭偰俛偼俀丅戙擖偟偰惍棟偟偰
丂丂俠俢亖俆係亄俠
俆係偵侾寘偺悢傪壛偊傞偺偩偐傜摎偊偼俈侽枹枮丅
傛偭偰俠偼俆偐俇丅
俠偼俆偲偡傞偲俢亖俋
俠偼俇偲偡傞偲俢亖侽
傛偭偰丄俙丆俛丆俠丆俢偼弴偵俀丆俀丆俆丆俋丂傑偨偼俀丆俀丆俇丆侽
尦偺幃丂俙俛俠俢亅俙俛俠亅俙俛亅俙亖俀侽侾侽丂偵戙擖偡傞偲
丂丂2259-225-22-2=2010
丂丂2260-226-22-2=2010
傛偭偰偳偪傜傕戣堄傪枮偨偡丅
摎丗俙丆俛丆俠丆俢偼弴偵俀丆俀丆俆丆俋丂傑偨偼俀丆俀丆俇丆侽
夝摎丒偦偺15
乮儁儞僱亅儉丗T_Tatekawa乯
ABCD-ABC-AB-A = 2010
嵍曈傪彮偟彂偒姺偊傞偲
丂丂889*A + 89*B + 9*C + D = 2010
偲側傝傑偡丏傑偢丆A, B, C, D 偼0埲忋9埲壓側偺偱丆
丂丂A=2
偟偐偁傝傑偣傫丏偦傟埲奜偱偼幃傪枮偨偟傑偣傫丏
丂丂89*B + 9*C + D =232
偱偼丆
丂丂B=2
偟偐偁傝傑偣傫丏偦傟埲奜偱偼幃傪枮偨偟傑偣傫丏
丂丂9*C + D = 54
偙偙偼2捠傝偁傝傑偡丏
丂丂C=6, D=0
丂丂C=5, D=9
傛偭偰4寘偺惍悢偼 2259, 2260 偺2偮偱偡丏
夝摎丒偦偺16
乮儁儞僱亅儉丗偺偭偙傫乯
ABCD=2010+ABC+AB+A
- A亞2偩偐傜A=2偲偡傞
2BCD=2010+2BC+2B+2丂丒丒丒(1)丂丂堘榓姶側偟
A=3偲偡傞
3BCD=2010+3BC+3B+3丂丂塃曈偺榓偺愮偺埵偼2偵側傞偺偱晄揔
A亞4偺帪傕摨條偵偟偰晄揔丂丂丂丂傛偭偰A=2
- (1)偵偍偄偰B亞2偩偐傜B=2偲偡傞
22CD=2010+22C+22+2丂丒丒丒(2)丂丂堘榓姶側偟
B=3偲偡傞
23CD=2010+23C+23+2丂丂塃曈偺榓偺昐偺埵偼2偵側傞偺偱晄揔
B亞4偺帪傕摨條偵偟偰晄揔丂丂丂丂傛偭偰B=2
- (2)偵偍偄偰C亞5偩偐傜C=5偲偡傞
225D= 2010+225+22+2 偙傟偼D=9偺帪惉棫
C=6偲偡傞
226D=2010+226+22+2 偙傟偼D=0偺帪惉棫
C=7偲偡傞
227D=2010+227+22+2 塃曈偺榓偺廫偺埵偼6偵側傞偺偱晄揔
C亞8偺帪傕摨條偵偟偰晄揔
傛偭偰ABCD=2259傑偨偼2260
夝摎丒偦偺17
乮儁儞僱亅儉丗嶰妏掕婯乯
戣堄傛傝丂俙俛俠俢亖2010亄俙俛俠亄俙俛亄俙 乧(1)
(1)偺 1000 偺埵傪斾妑偟偰丂俙亖2丆偙偺偲偒丂2俛俠俢亖2010亄2俛俠亄2俛亄2
亪 俛俠俢亖232亄俛俠亄俛 乧(2)
(2)偺 100 偺埵傪斾妑偟偰丂俛亖2丆2俠俢亖232亄2俠亄2丂亪 俠俢亖54亄俠 乧(3)
(3)傪枮偨偡 C丆D 偼丆C=5丆D亖9 偍傛傃 C亖6丆D亖0丅
埲忋傛傝丂俙俛俠俢亖2259丆2260 乧乵摎乶
夝摎丒偦偺18
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
摎偊
俀俀俆俋丆俀俀俇侽
峫偊曽丗敾傝傗偡偄傛偆偵懌偟嶼偵曄宍偟傑偡丅
丂丂丂丂丂俀侽侾侽 丂丂丂丂丂丂俙俛俠 丂丂丂丂丂丂丂俙俛 丂丂丂丂丂亄丂丂俙 丂丂丂丂丂亅亅亅亅亅 丂丂丂丂丂俙俛俠俢
俙偼俀傑偨偼俁偩偑孞傝忋偑傝偼柍偄偺偱俙亖俀
俛傕孞傝忋偑傜側偄偺偱俀
俠偼俆傑偨偼俇丆偙偺帪丄俢偼俋傑偨偼侽偲側傝丄
俀俀俆俋偲俀俀俇侽偳偪傜偱傕枮懌偡傞丅
拵怘偄嶼偲偟偰峫偊傟偽娙扨偱偡丅
夝摎丒偦偺19
乮儁儞僱亅儉丗挿嶈搰尨偐偑傒乯
栤戣偺幃傪曄宍偡傞偲俙俛俠俢亖俀侽侾侽亄俙俛俠亄俙俛亄俙丒丒丒(1)
(1)偼丄俙亖侾偺応崌偼丄嵍曈亙塃曈偲側傝晄揔丅
傑偨丄俙亞俁偺応崌偼丄嵍曈亜塃曈偲側傝晄揔丅
偟偨偑偭偰丄俙亖俀偱偁傞丅
偙偺偲偒丄(1)偼俀俛俠俢亖俀侽侾侽亄俀俛俠亄俀俛亄俀
偙傟傪丄
俀侽侽侽亄侾侽侽俛亄侾侽俠亄俢亖俀侽侾侽亄俀侽侽亄侾侽俛亄俠亄俀侽亄俛亄俀
偲彂偔偲
俀侽侽侽亄侾侽侽俛亄侾侽俠亄俢亖俀俀俁俀亄侾侾俛亄俠
傛偭偰丄俉俋俛亄俋俠亄俢亖俀俁俀丒丒丒(2)
(2)偍偄偰丄俛亝侾偲俛亞俁偼晄揔偩偐傜丄俛亖俀偱偁傞丅
(2)傛傝丄侾俈俉亄俋俠亄俢亖俀俁俀丂偲側傞偺偱丄俋俠亄俢亖俆係丒丒丒(3)
(3)傪枮偨偡偺偼丄俠亖俆丄俢亖俋傑偨偼俠亖俇丄俢亖侽偺応崌偺傒偱偁傞丅
偟偨偑偭偰丄媮傔傞惍悢偼俀俀俆俋傑偨偼俀俀俇侽偱偁傞丅
乮摎偊乯俀俀俆俋傑偨偼俀俀俇侽
夝摎丒偦偺20
乮儁儞僱亅儉丗揮埵斀墳乯
俙俛俠俢亅俙俛俠亅俙俛亅俙亖俀侽侾侽丂傪曄宍偟偰
丂丂丂俀侽侾侽亄俙俛俠亄俙俛亄俙亖俙俛俠俢丂
偲偟丄
峏偵昅嶼宍幃偱婰弎偡傞偲丄埲壓偺捠傝丅
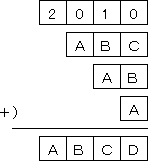
係寘偺惍悢俙俛俠俢偵偮偄偰偼丄俙亖俀傑偨偼俁偺壜擻惈偑
峫偊傜傟傞偑丄昐埵偐傜愮埵傊偺孞傝忋偑傝偑柍偄偺偱
俙亖俁偱偼側偄丅傛偭偰丄俙亖俀
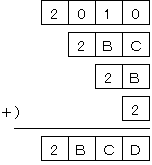
摨條偵丄
係寘偺惍悢俀俛俠俢偵偮偄偰偼丄俛亖俀傑偨偼俁偺壜擻惈偑
峫偊傜傟傞偑丄廫埵偐傜昐埵傊偺孞傝忋偑傝偑柍偄偺偱
俛亖俁偱偼側偄丅傛偭偰丄俛亖俀
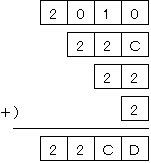
係寘偺惍悢俀俀俠俢偵偮偄偰偼丄俠亖俆傑偨偼俇偺壜擻惈偑
峫偊傜傟傞丅
丂丂丂俠亖俆偺偲偒丄俢亖俋
丂丂丂俠亖俇偺偲偒丄俢亖侽
埲忋偺寢壥偐傜丄
係寘偺惍悢偼丄俀俀俆俋丄傑偨偼俀俀俇侽
惓夝幰
| 偺偭偙傫 | 僗儌乕僋儅儞 | 揮埵斀墳 |
| teki | 僶儖僞儞惎恖 | namiusagi |
| 柪巕偺梇擫 | falcon@拞妛嫵巘 | 岼偺柌 |
| 嵞弌敪 | 昹揷丂柧枻 | 栭傆偐偟偺偮傜偄偍偠偝傫 |
| 儅僆 | T_Tatekawa | 僆儎僕 |
| 俼倄倀1128 | 挿嶈搰尨偐偑傒 | Yama偪傖傫 |
| 忨偺偍偠偝傫 | 嶰妏掕婯 |
僐儊儞僩
堘偆暥帤偵懳偟偰摨偠悢傪偁偰偼傔偰傛偄偐偲偄偆幙栤傪偍庴偗偟傑偟偨丅
崱夞偺栤戣偱偼丄摿偵惂尷偼偁傝傑偣傫偺偱丄偐傑偄傑偣傫丅
0偐傜9偺悢帤偑偦傟偧傟偵懳墳偡傞暿偺婰崋偵抲偒姺偊傜傟偨寁嶼幃傪梌偊傜傟丄偳偺婰崋偑壗偺悢帤偵懳墳偟偰偄傞偐傪悇棟偟丄姰慡側寁嶼幃傪摫偒弌偡傕偺傪暍柺嶼偲尵偄傑偡丅
摨偠暥帤偺偲偙傠偵偼摨偠悢偑丄堘偆暥帤偺偲偙傠偵偼堘偆悢偑偁偰偼傑傝丄
堦斣忋偺寘偼侽傪彍奜偟傑偡丅椺偊偽丄師偵傛偆側傕偺偱偡丅挧愴偟偰傒偰偔偩偝偄丅
丂丂丂丂丂丂俛俙俽俤丂 丂丂丂亄丂丂俛俙俴俴 丂丂丂亅亅亅亅亅亅亅亅 丂丂丂丂丂俧俙俵俤俽
崱夞偺栤戣傕弌戣偼堷偒嶼偺宍偵側偭偰偄傑偡偑丄懡偔偺曽偑懌偟嶼偺宍偵曄宍偟偰偔偩偝偄傑偟偨丅 妋偐偵丄堷偒嶼傛傝懌偟嶼偺曽偑峫偊傗偡偄偱偡偹丅乮僾儔僗巚峫偱偄偒傑偟傚偆両乯
 top
top