栤戣156丂惎嵗偺栤戣
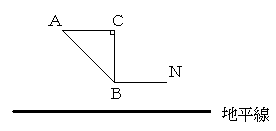
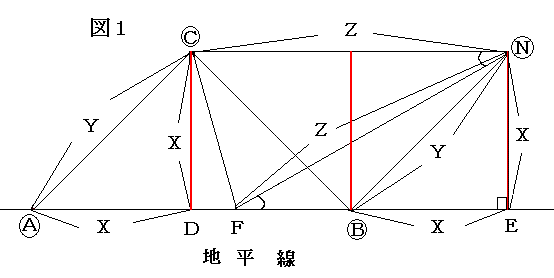
屵屻俇帪30暘丄杒偺嬻偵杒嬌惎俶偲捈妏擇摍曈嶰妏宍偺宍偵側傞惎俙丄俛丄俠偑
恾偺傛偆偵尒偊傑偟偨丅
乮俶偺嵍偵俛丄俛偺忋偵俠丄俠偺嵍偵俙偱丄俶俛亖俛俠亖俠俙乯丅
壗帪娫偐屻偵惎俙偲惎俛偑摨帪偵抧暯慄偵捑傒傑偟偨丅偦偺偁偲惎俠偑捑傒傑偟偨丅
惎俠偑捑傫偩帪崗傪媮傔偰偔偩偝偄丅
偨偩偟丄惎俙丄俛丄俠偼杒嬌惎偺廃傝傪24帪娫偐偗偰斀帪寁廃傝偵侾廃偟傑偡丅
傑偨丄抧暯慄偼悈暯側捈慄偲偟傑偡丅
栤戣偺弌揟
嶼悢僆儕儞僺僢僋偵挧愴
嶼悢僆儕儞僺僢僋埾堳夛曇
島択幮僽儖乕僶僢僋僗
2005擭僼傽僀僫儖栤戣
(弌戣丗壨栰廏庽)
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
摎偊
屵屻侾侾帪俁侽暘
峫偊曽丗俙俛俶俠偼暯峴巐曈宍偱丄俙俛偑抧暯慄偵棃傞偵偼係俆搙夞揮偡傞丅
傑偨丄俶偐傜抧暯慄偵壓傠偟偨悅慄偺懌傪俫偲偡傞偲
丂丂俶俠亖俀俶俫
屘偵俠偑抧暯慄偵棃傞偲偒偼丄惓尫偑侾乛俀偲側傞俁侽搙偝傜偵摦偔偙偲偵側傞丅
侾帪娫偵侾俆搙偢偮夞揮偡傞偺偱乮係俆亄俁侽乯乛侾俆亖俆帪娫屻
夝摎丒偦偺2
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
崱夞偺栤戣偼...AB 偑摨帪偵悈暯慄偵杤偡傞偲偒偺恾傪昤偄偰傒偨傜...
C 偑悈暯慄偵堏摦偡傞傑偱偺妏搙偼...NC=併2 : 悈暯慄傑偱偺崅偝=併2/2 偲側傞偺偱...
妏搙偵偡傞偲 30亱側偺偱...
AB 偑悈暯偵側傞傑偱 45亱偲壛偊偰...
24*((30+45)/360)=2+3=5
6:30+5:00=11:30 pm
偵側傝傑偡偹 侓
夝摎丒偦偺3
乮儁儞僱亅儉丗柪巕偺梇擫乯

惎俙偲惎俛偑摨帪偵抧暯慄偵捑傫偩偲偒偺惎俠偺埵抲傪俢
惎俠偑抧暯慄偵捑傫偩偲偒偺惎俠偺埵抲傪俤偲偍偔丅
惎俙偲惎俛偑摨帪偵抧暯慄偵捑傫偩偲偒
捈慄俙俛偑悈暯側偺偱丄捈慄俶俢傕悈暯偵側傞丅
偙偺偲偒偺夞揮妏搙偼係俆搙丅
俶俛亖俛俠亖俠俙偺挿偝傪侾偲抲偔偲
嶰妏宍俙俛俠丄嶰妏宍俶俛俠丄偺柺愊偑侾乛俀側偺偱丄
嶰妏宍俢俶俤偼丄柺愊偑侾乛俀丄幬曈偑併俀
幬曈偵悅慄傪壓傠偟偨偲偒丄偦偺悅慄偺挿偝偼侾乛乮併俀乯
幬曈丗悅慄偺挿偝偺斾偑俀丗侾偺捈妏嶰妏宍偺妏搙偼丄
俋侽搙丄俇侽搙丄俁侽搙丄偱偁傞偺偱丄妏俢俶俤偼俁侽搙丅
傛偭偰丄埲忋傛傝丄惎俠偑抧暯慄偵捑傫偩偲偒偺夞揮妏搙偼俈俆搙丅
堦擔偱俁俇侽搙夞揮偡傞惎偑俈俆搙夞揮偡傞偺偵昁梫側帪娫偼丄
俀係帪娫仏俈俆搙乛俁俇侽搙亖俆帪娫丅
屵屻俇帪30暘傛傝俆帪娫宱夁偟偨帪崗偼屵屻11帪30暘丅
摎丗屵屻11帪30暘
夝摎丒偦偺4
乮儁儞僱亅儉丗AND乯
摎偊丗侾侾帪俁侽暘

乮弶婜忬懺偐傜暘偐傞偙偲乯
N丒A丒B丒C偼掕媊傛傝丄暯峴巐曈宍偵側偭偰偍傝丄N俛亖俛俠亖俠俙偺挿偝傪侾偲
偡傞偲丄僺僞僑儔僗偺掕棟偐傜俶亅俙亖併俆丄N亅C亖併俀丂偲側傝丄傑偨丄
暯峴慄俶亅俠偲俙亅俛偺娫偺嫍棧偼丄併俀亐俀偲側傝傑偡丅
傑偨丄弶婜忬懺乮俇帪俁侽暘乯帪揰偺悈暯慄偲慄暘俶亅俠偲偺妏搙偼丄掕媊
乮俶俛亖俛俠乯傛傝係俆搙偲側傝傑偡丅
乮惎俙丒俛偑摨帪偵悈暯慄偵捑傫偩偙偲偐傜暘偐傞偙偲乯
偙偙偱丄傑偢俙偲俛偼摨帪偵悈暯慄偵捑傫偩偺偱偡偐傜丄偦偺偲偒偼杒嬌惎俶偲
惎俠偼悈暯慄偲暯峴偵側偭偰偄傞偙偲偵側傝傑偡丅丂偙偺偙偲偐傜悈暯慄偲
杒嬌惎偺娫偺嫍棧偼丄併俀亐俀偲側傝傑偡丅
乮惎俠偑悈暯慄偵捑傓帪崗傪憐掕偟偰暘偐傞偙偲乯
偄傑丄惎俠偑悈暯慄偵捑傫偩忬懺傪峫偊傞偲杒嬌惎俶偲惎俠偺娫偺嫍棧偼丄
併俀偱偁傝丄惎俠偲悈暯慄偺嫍棧偼併俀亐俀偲側傝傑偡偐傜丄惎俠偑悈暯慄偵
捑傫偩帪揰偱偺慄暘俶亅俠偲悈暯慄偺妏搙偼丄俽倝値乮倃乯亖侾乛俀偐傜俁侽搙偲
側傝傑偡丅
乮偙傟傑偱丄暘偐偭偨偙偲傪惍棟偡傞偲乯
埲忋傛傝丄媮傔傞摎偊偼丄俇帪俁侽暘傛傝丄俈俆搙乛俁俇侽搙妏搙偑夞揮偟偨
帪崗傪媮傔傟偽傛偄偙偲偵側傝傑偡丅
俈俆搙偼乮侾帪娫亖侾俆搙傛傝乯俆帪娫偱偡偐傜丄媮傔傞惎俠偑悈暯慄偵捑傫偩
帪崗偼丄侾侾帪俁侽暘偲側傝傑偡丅
夝摎丒偦偺5
乮儁儞僱亅儉丗儅僆乯
夝摎丗屵屻11帪30暘
AC=BN,AC//BN傛傝仩ABNC偼暯峴巐曈宍丅
BN=1 偲偡傞偲丄CN=併2 , AN=併5偲側傞丅
A,B偑抧暯慄偵捑傓偲偒偺A,B,C埵抲傪A',B',C'
C偑抧暯慄偵捑傓偲偒偺埵抲傪C"偲偡傞丅
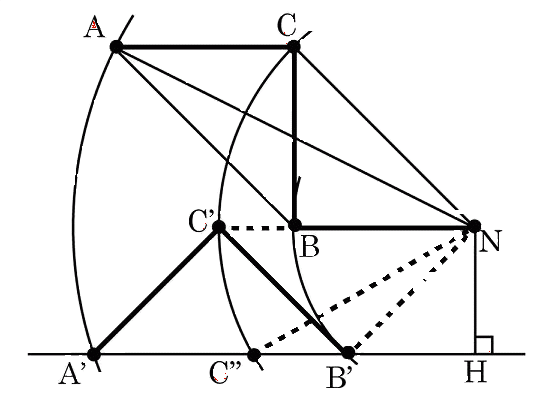
AB偑抧暯慄偵廳側傞偲偒丄C'N//A'B'傛傝丄
揰B偼C'N忋偵偁傞丅
揰N偐傜抧暯慄偵悅慄傪壓傠偟丄岎揰傪H偲偡傞偲丄
仮NHB'偼捈妏擇摍曈嶰妏宍偱丄NB'=1 傛傝 NH=併2/2
NC"=併2傛傝丄仮NC"H偼 1:2:併3偺捈妏嶰妏宍偲側傝丄
佢C"NH=60亱偲側傞丅
傛偭偰佢CNC"=佢CNC'+佢C'NH-佢C"NH
=(45+90-60)亱
=75亱
揰C偑抧暯慄偵捑傓傑偱偵偐偐傞帪娫偼
丂丂24亊75亐360=5
偙傟傛傝丄揰C偑抧暯慄偵捑傓帪崗偼
5帪娫屻偺 屵屻11帪30暘
夝摎丒偦偺6
乮儁儞僱亅儉丗嵞弌敪乯
惎俙丄俛偼抧暯慄偵扝傝拝偔傑偱偵俶傪拞怱偵佢俛俶俠亖係俆並偩偗夞揮偟傑偡丅
偮偓偵丄慄暘俙俛忋偵俠俶亖俢俶偲側傞傛偆偵揰俢傪偲傞偲
佢俢俶俠亖俁侽並偲側傝丄
乮佹丂揰俢偐傜慄暘俶俠偵悅慄俢俤傪壓傠偡偲俢俤丗俢俶亖侾丗俀乯
揰俠偑俶傪拞怱偵慄暘俙俛偵扝傝拝偔傑偱偵俁侽並偩偗夞揮偟傑偡丅
偟偨偑偭偰丄屵屻俇帪俁侽暘偐傜惎偨偪偼
杒嬌惎傪拞怱偵俈俆並偩偗夞揮偟偨傛偆偵尒偊傑偡丅
偦傟偵梫偟偨帪娫偼
俀係亊俈俆亐俁俇侽亖俆丂帪娫偱偡丅
偙偺偙偲偐傜惎俠偑捑傫偩帪娫偼屵屻侾侾帪俁侽暘偱偁傞偙偲偑暘偐傝傑偡丅
夝摎丒偦偺7
乮儁儞僱亅儉丗嶰妏掕婯乯
乽惎俙偲惎俛偑摨帪偵抧暯慄偵捑傫偩乿 偲偒丆
慄暘 NB 偼斀帪寁夞傝偵 45並 夞揮偟偰恾偺傛偆偵側偭偨丅
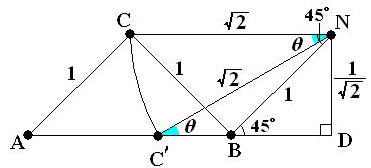
慄暘 NC 偑偝傜偵兤夞揮偟惎俠偑捑傓偲偒丆恾偺傛偆偵丆佢CNC'亖佢NC'D 偱
丂丂sin佢NC'D亖ND/NC'亖1/2
偩偐傜丆兤亖30並
惎乆偼丆杒嬌惎俶偺夞傝傪侾帪娫偵 15並夞揮偡傞偐傜丆45並亄30並 夞揮偡傞偺偼 5 帪娫屻丅
傛偭偰丆惎俠偑抧暯慄偵捑傓偺偼丆屵屻11帪30暘丅乧乵摎乶
夝摎丒偦偺8
乮儁儞僱亅儉丗namiusagi乯
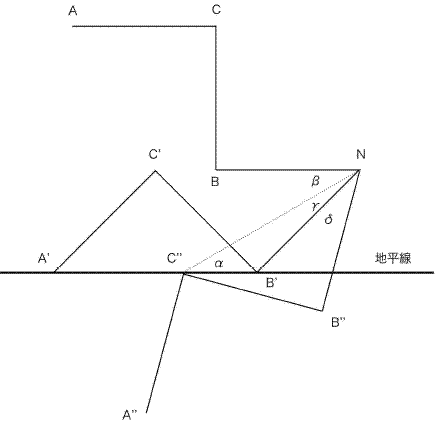 惎A偲惎B偑摨帪偵抧暯慄偵捑傫偩偺偱丄恾偺A',C',B',N偺條偵側傞丅偙偺帪45亱夞揮偟偨偙偲偵側傞丅
惎A偲惎B偑摨帪偵抧暯慄偵捑傫偩偺偱丄恾偺A',C',B',N偺條偵側傞丅偙偺帪45亱夞揮偟偨偙偲偵側傞丅
偙偙偐傜恾偺A'',C'',B'',N偺條偵側偭偨帪偑惎C(C'')偑捑傫偩帪偱偁傞丅
恾偺妏兛偼30亱偩偐傜丄兝=30亱丄兞=15亱丄兟=30亱偱屵屻6帪30暘偐傜75亱夞揮偟偨偙偲偵側傞丅
24帪娫偱堦廃乮360亱乯偡傞偺偱
丂丂丂(75/360)*24=5
亪屵屻11帪30暘
夝摎丒偦偺9
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎丂屵屻11帪30暘偱偡丅
俙丆俛偺惎偑抧暯慄偵捑傓偺偼45亱夞揮偟偨帪偱偁傞丅
廬偭偰丂堦帪娫偺夞揮妏搙偼丂(俁俇侽亱)/俀係亖15亱側偺偱丂(係俆亱)/(侾俆亱)亖3丂帪娫丂屻偲側傞丅
壓偺恾偼俙丆俛偺惎偑抧暯慄偵捑傫偩帪偺俠惎偺埵抲偱偡丅
俶俤亖俠俢丂挿偝傪X偲偡傞丅
俙俠亖俠俛亖俛俶丂挿偝傪Y偲偡傞丅
俶俠亖俶俥丂挿偝傪Z偲偡傞丅
佢俠俶俥亖佢俶俥俤丂偼嶖妏偱摨偠妏搙偱偡丅
X亖1偲偟偰Y傪媮傔傞偲Y亖併2
Z亖併(Y2+Y2 )亖2偲側傝傑偡丅
佢俶俥俤傪媮傔傑偡丅
SIN兤亖倃/倅亖侾/俀亖0.5
廬偭偰妏搙偼30亱偵側傝傑偡丅
帪娫偼丂俁侽亱/侾俆亱亖2丂帪娫屻偲側傞丅
俠惎偑抧暯慄偵捑傓偺偼丄屵屻6帪30暘亄3帪娫亄2帪娫亖屵屻11帪30暘丂偲側傝傑偡丅
夝摎丒偦偺10
乮儁儞僱亅儉丗傗側偣乯

惎娫嫍棧俶丆俛亖俛丆俠亖俠丆俙偲
惎娫傪寢傫偩慄丄俶丆俛偲俛丆俠捈岎偡傞
枖俛丆俠偲俠丆俙傕捈岎偡傞
慄俶丆俛偲俠丆俙偼抧暯慄偲暯峴偵側傞
尰嵼偺帪娫偼屵屻俇帪敿
俀係帪娫偱侾廃偡傞
彮偟偼夝傝傗偡偄偐偲巚偭偰杒嬌惎俶傪拞怱偵墌傪昤偄偰傒偨
梌偊傜傟偨忦審偐傜抧暯慄偐傜杒嬌惎俶偺崅偝偼惎俶丆俠娫偺敿暘偵側傝傑偡丅
恾偱偼俙乫丄俛乫丄俠乫偺帪偑惎俙丆俛偑摨帪偵抧暯慄偵捑傓帪偱偡丅
媮傔傞偺偼俠偑抧暯慄偵捑傓帪娫偱偡偐傜捑傓偲偒偺惎俠偺抧揰傪俠乭偲偡傟偽
佢俠丆俶丆俠乭偺妏搙倂偑夝傟偽
俠偑捑傓傑偱偺宱夁帪娫偑夝傝傑偡丅
佢俛丆俶丆俠偼係俆亱側偺偱巆傝偺佢倃偑偄偔傜偐偱偡偑
俶偐傜俠乭偵慄傪堷偔偲暯峴慄偵岎傢傞慄暘偑側傫偨傜偐傫偨傜偺掕棟偱
佢倄亖佢倃
俶偐傜抧暯慄偵捈岎偡傞慄傪堷偒岎傢傞偲偙傠傪俢偲偡傞偲
慄暘俢丆俠乭亖俶丄俢亊俀
佢俶丆俢丆俠乭捈妏側偺偱扤偐偝傫偺嶰妏宍偺掕棟偐傜
佢倃亖俁侽亱亖佢倄偑夝傝傑偡丅
偙傟偐傜
佢倂亖係俆亱亄俁侽亱偵側傞
俀係帪娫偱侾廃偡傞偺偱
俀係亊俈俆亐俁俇侽亖俆乮帪娫乯
屵屻俇帪俁侽暘亄俆帪娫亖屵屻侾侾帪俁侽暘
摎偊
屵屻侾侾帪敿
夝摎丒偦偺11
乮儁儞僱亅儉丗僆儎僕乯
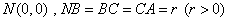 偲偡傞偲
偲偡傞偲
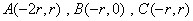 偲側傞
偲側傞
愭偢丄俙丆俛偑抧暯慄偵摨帪偵捑傓忬嫷傪峫偊傞丅
妏懍搙偼丄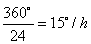
俙俠偲抧暯慄,丂傑偨俛俶偲抧暯慄偺側偡妏搙偼,
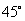 偱偁傝丄
偱偁傝丄
妏懍搙傪峫偊傞偲丄屵屻俇帪俁侽暘偺係俆亐侾俆亖俁帪娫屻偺
屵屻俋帪俁侽暘
偙偺帪丂杒嬌惎偐傜抧暯慄偵偍傠偟偨悅慄偺懌傪俫偲偡傞偲挿偝丂丂
丂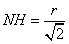
師偵,丂俠偑抧暯慄偵捑傓忬嫷傪峫偊傞偲丂 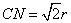 丂丂嶰妏宍俶俠俫傪峫偊傞偲丂
俶俫丗俠俶丗俠俫亖侾丗俀丗
丂丂嶰妏宍俶俠俫傪峫偊傞偲丂
俶俫丗俠俶丗俠俫亖侾丗俀丗 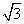
廬偭偰丂佢俶俠俫亖 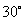 廬偭偰丂佢俶俠俛亖
廬偭偰丂佢俶俠俛亖 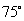
妏懍搙傪峫偊傞偲丂屵屻俇帪俁侽暘偺丂俈俆亐侾俆亖俆帪娫屻偺
屵屻侾侾帪俁侽暘丂
亪丂屵屻丂侾侾帪俁侽暘
夝摎丒偦偺12
乮儁儞僱亅儉丗偺偭偙傫乯

惎俙偑抧暯慄偵捑傓帪偵偦傟偑愯傔傞埵抲傪俹丄
惎俛偑抧暯慄偵捑傓帪偵偦傟偑愯傔傞埵抲傪俻丄
惎俠偑抧暯慄偵捑傓帪偵偦傟偑愯傔傞埵抲傪俼偲偡傞丅
俹丄俻丄俼偼悈暯側捈慄忋偵偁傞
俶俛亖俛俠亖俠俙亖侾 偲偟
俶乮侽丄侽乯丄俙乮亅俀丄侾乯丄俛乮亅侾丆侽乯丄俠乮亅侾丄侾乯偲偡傞
俛偺婳愓偼 x2+y2=1丒丒丒(1)
俠偺婳愓偼 x2+y2=2丒丒丒(2)偱偁傞
仮俶俙俛佭仮俶俹俻丄佢俙俛俶亖135亱偩偐傜
俶俻偺曽掱幃偼 y=x丒丒丒(3)
(3)傪(1)偵戙擖偟偰 俻乮亅1/併2丄亅1/併2乯
傛偭偰俼偺y嵗昗偼亅1/併2
y亖亅1/併2 傪(2)偵戙擖偟偰
俼偺x嵗昗偼亅併3/併2
俶俛偺墑挿偵俼偐傜悅慄傪壓偟丄偦偺懌傪俫偲偡傞偲
俼俫丗俫俶丗俶俼亖1丗併3丗2
傛偭偰佢俛俶俼亖30亱
佢俠俶俼亖佢俠俶俛亄佢俛俶俼亖45亱亄30亱亖75亱
15亱偺夞揮偱1帪娫偩偐傜
75亱偺夞揮偱偼5帪娫
俠偑捑傓偺偼5帪娫屻偺屵屻11帪30暘
夝摎丒偦偺13
乮儁儞僱亅儉丗haya乯
揰 C 偑悈暯慄偵杤偡傞帪崗偼 11帪30暘 偱偡丅
亂夝偒曽亃
揰 N 傪拞怱偵夞揮偟偰 A, B 揰偑摨偠崅偝偵暲傇偵偼丄慄暘 AB 偺墑挿慄偲悈暯慄偺側偡妏搙丄
偮傑傝 45亱夞揮偡傞昁梫偑偁傞丄偙偺偨傔偺帪娫偼
丂丂24 x 45 / 360 = 3 (H)
偙偙偐傜揰 C 偑悈暯慄偵杤偡傞偵偼丄N 傪拞怱偲偟偰敿宎 CN 偺墌屖傪昤偄偨帪偵慄暘 AB 偲岎傢傞揰傪 D 偲偟偰丄
兤 = 佢CND 偩偗峏偵夞揮偝偣傞昁梫偑偁傞丅
弌戣偺恾偱丄N 傪尨揰偲偡傞捈岎嵗昗傪峫偊丄B 偺嵗昗傪 (-1,0)丄C 傪 (-1,1)偲偲傞丅
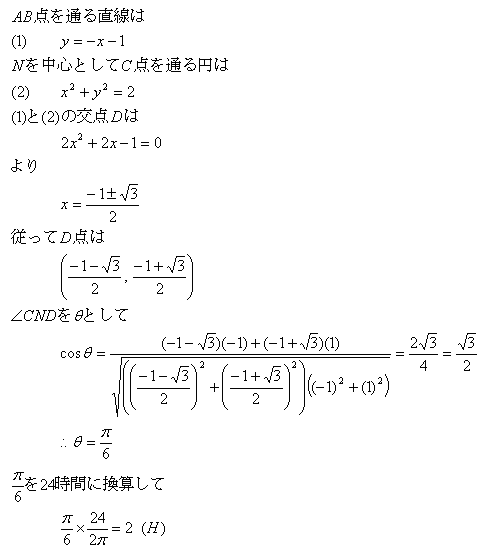

廬偭偰夞揮偵昁梫側帪娫偼丄
丂丂3 + 2 = 5 (H)
帪崗偺弶婜抣偼 6:30 偱偁傞偐傜丄揰 C 偑悈暯慄偵杤偡傞帪崗偼
丂丂11:30
偲側傞丅
夝摎丒偦偺14
乮儁儞僱亅儉丗偙偨偮乯
N傪拞怱偵24帪娫偱360亱夞揮偡傞偙偲偐傜1帪娫偱15亱亖 兾/12夞揮偡傞
BN偺嫍棧傪1偲偟偰丄N傪嵗昗偺拞怱偲傒傞偲
惎C偺嵗昗偼(Xc , 併2sin(3兾/4 + t兾/12) )偲側傞丅
仸t偼P.M6:30偐傜偺帪娫乮扨埵偼乽帪娫乿乯
慄暘AB偲慄暘CN偼暯峴偱偁傞偙偲偐傜惎A,B偑抧暯慄偵拝偄偨帪丄惎C,N傕抧暯慄偲暯峴偵墶偵暲傫偱偄傞忬懺
偦偟偰丄偙偺帪惎C偺抧暯慄偐傜偺崅偝偼併2/2偱偁傞丅
傛偭偰惎C偑捑傓帪偼C偺嵗昗偑(Xc1 , -併2/2) 偲側傞
併2sin(3兾/4 + t兾/12) = -併2/2丂傪枮偨偡t偼
Sin(3兾/4 + t兾/12) = -1/2丂仺丂3兾/4 + t兾/12 =7兾/6
傛偭偰丂t = 5
惎C偼P.M6:30偐傜5帪娫屻偵捑傓
摎偊偼屵屻11帪30暘
夝摎丒偦偺15
乮儁儞僱亅儉丗僔儏儗乕僨傿儞僈乕偺嶰栄擫乯
亙曽恓亜
惎俙丄俛偑捑傓弖娫偺忬懺偐傜抧暯慄偲俶丄俠偲偺娭學傪帵偟丄
惎俶偍傛傃俠傪寢傇慄暘偺嫇摦傪丄俶傪拞怱偲偡傞扨埵墌偐傜峫嶡偡傞丅
亙夝摎亜

屵屻6帪30暘傪弶婜帪崗偲偡傞丅宖戣偺恾傛傝丄弶婜帪崗偵偍偄偰俙俠偲俛俶偼暯峴偱丄
傑偨抧暯慄偲偦傟偧傟暯峴偱偁傞偲夝庍偡傞丅
俶俛亖俛俠亖俠俙丄偐偮佢俶俠俛偼捈妏側偺偱丄嶰妏宍俶俛俠偲嶰妏宍俙俛俠偼屳偄偵崌摨偱偁傞丅
傛偭偰丄俙俛俶俠偼暯峴巐曈宍偱偁傞丅
戣堄傛傝丄惎俶偐傜傒偨惎俙丄俛丄俠偺憡懳揑側埵抲娭學偼曄傢傜側偄偺偱丄
惎俙丄俛偑捑傓偲偒丄懄偪俙俛偑抧暯慄偲愙偡傞偲偒丄俠俶偼抧暯慄偲暯峴偲側傞丅
偙偙偱丄俠俶亖俙俛亖侾偲偍偔丅偙偺偲偒丄嶰妏宍俙俛俠偲嶰妏宍俶俛俠偼崌摨側捈妏擇摍曈嶰妏宍側偺偱丄
丂丂俙俠亖俠俛亖俛俶亖1/併2
俶偐傜抧暯慄偵壓傠偟偨悅慄偲抧暯慄偲偺岎揰傪俹丄
摨條偵俠偐傜抧暯慄偵壓傠偟偨悅慄偲抧暯慄偲偺岎揰傪俫偲偍偔丅
嶰妏宍俙俠俫偲嶰妏宍俛俠俫偼崌摨偱偁傝乮佹幬曈偲侾塻妏偑偦傟偧傟摍偟偄乯丄
偦傟偧傟捈妏擇摍曈嶰妏宍偲側傞丅
傑偨丄俙俠偲俛俶偼屳偄偵暯峴巐曈宍偺懳曈側偺偱丄
丂丂俙俠亖俛俶丄俙俠//俛俶丄佢俠俙俫亖佢俶俛俹丅
傛偭偰丄嶰妏宍俙俠俫偼嶰妏宍俛俶俹偲傕崌摨偱偁傞乮佹幬曈偲侾塻妏偑偦傟偧傟摍偟偄乯丅
偝偰丄嶰妏宍俙俠俫偲嶰妏宍俛俠俫偼崌摨側捈妏擇摍曈嶰妏宍側偺偱丄
嶰妏宍俙俛俠偵偍偄偰俫偼慄暘俙俛傪擇摍暘偟丄偐偮偦偺挿偝偼俠俫偲傕摍偟偄丅
俙俛亖侾偲偍偄偨偺偱偁傞偐傜丄俙俫亖俫俛亖俠俫亖1/2
嶰妏宍俙俠俫偼嶰妏宍俛俶俹偲傕崌摨側偺偱丄俠俫亖俶俹亖1/2
廬偭偰丄惎俶偼抧暯慄偐傜1/2偺崅偝偵偁傞偙偲偑傢偐傞丅
偙偙偱丄惎俶傪拞怱偲偡傞扨埵墌乮恀搶偐傜偺斀帪寁夞傝傪妏搙偺惓偲偡傞乯傪偲傞偲丄偙傟偼惎俠偺婳愓偲側傝丄
抧暯慄偼倷亖-1/2偺捈慄偱昞偣傞丅
惎俙丄俛偑捑傓偲偒偺俶俠偺妏搙偼兾丄俶俛偺妏搙偼兾亄兾/4偲側傞丅
弶婜帪崗偱偺俶俛偺妏搙偼兾側偺偱丄弶婜帪崗偐傜俙丄俛偑捑傓傑偱偵
俙丄俛丄俠偑堏摦偟偨妏搙偼偦傟偧傟兾/4偱偁傞丅
偙偙偐傜丄弶婜帪崗偱偺俶俠偺妏搙偼
丂丂兾-兾/4亖3兾/4丂丒丒丒(1)
偲媮傑傞丅
堦曽丄俠偑捑傫偩偲偒偼丄俠偺倷嵗昗偑-1/2偲側傞丅
懄偪丄偙偺偲偒偺俶俠偺妏搙兤偲偍偄偨偲偒丄sin兤亖-1/2丄偙傟傪戞3徾尷偺妏偲偟偰夝偄偰丄
丂丂兤亖7兾/6丂丒丒丒(2)
弶婜帪崗偐傜俠偑捑傓傑偱偵堏摦偟偨妏搙偼丄
丂丂(2)-(1)亖5兾/12丂丒丒丒(3)
偲媮傑偭偨丅
偝偰丄帪娫偺曄壔検傪嚈t丄妏搙偺曄壔検傪嚈兤偲偍偔偲丄惎俠偼24帪娫偱俶偺廃傝傪堦廃偡傞偙偲偐傜丄
丂丂嚈兤亖2兾嚈t/24 丟乮嚈t偺扨埵偼"帪娫"乯
偲偄偆娭學幃偑摼傜傟傞丅偙偙偵嚈兤亖(3)亖5兾/12傪戙擖偟偰嚈t偵偮偄偰夝偔偲丄
丂丂嚈t亖5(帪娫)
弶婜帪崗偑屵屻6帪30暘偩偭偨偺偱丄惎俠偑捑傓帪崗偼屵屻11帪30暘丅
夝摎丒偦偺16
乮儁儞僱亅儉丗棔偺嬻乯
俶偼杒嬌惎偱偁傞偐傜丄晄摦偱偁傞偲偡傞丅
忬懺嘥偵偍偄偰丄俶偐傜抧暯慄偵堷偄偨悅慄傪揰俷偲偡傞乮偙偺揰傕晄摦偱偁傞乯丅
捈慄俛俠偵偮偄偰俶偲懳徧側揰傪俶乫偲偡傞丅
傑偨丄俙俠亖俠俛亖俛俶亖俶乫俛亖a丂偲偡傞丅
丂丂俙俠亖俶俛 丆佢俙俠俛亖佢俶俛俠亖俋侽亱(乧(1))丆俛俠偼堦抳
偙偺俁揰傛傝丂仮俙俛俠佭仮俶俠俛
丂丂亪 俙俛亖俶俠
傑偨丄仮俙俛俠偼擇摍曈嶰妏宍偱偁傝丄(1)傛傝
丂丂佢俠俙俛亖佢俠俛俙亖係俆亱
丂丂亪 俙俛亖併2 a乮亖俶俠乯
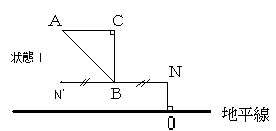
忬懺嘥偱丄俶乫偼俙偺恀壓偵埵抲偡傞偺偱丄
丂丂俶乫俛俙亖係俆亱丂偲側傞偺偱丄捈慄俙俛偲悈暯慄偲偼45亱偺妏搙傪側偟偰偄傞丅
値帪娫屻偵俙偲俛偑摨帪偵悈暯慄偵捑傓偲偒丄俙俛偼悈暯慄偲暯峴乮堦抳乯偱偁傞偐傜丄
値帪娫偺娫偵係俆亱俙丆俛偼堏摦偟偨偲暘偐傞丅
偲偙傠偱丄俀係帪娫偱堦廃乮俁俇侽亱夞揮乯偡傞偲偄偆偙偲偼侾帪娫偱侾俆亱夞揮偡傞偲偄偆偙偲偱偁傞丅
傛偭偰丄値*侾俆亖係俆丂丂亪値亖俁丂乮俋帪俁侽暘偵捑傫偩乯乧(2)
側偍丄俙俛亖俠俶 丆 俙俠亖俛俶傛傝巐妏宍俙俛俶俠偼暯峴巐曈宍偱偁傞偐傜
俙俛偑悈暯慄偲暯峴偱偁傞偲偒丄俠俶傕悈暯慄偲暯峴偱偁傞丅
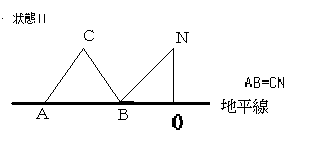
師偵丄恾偵偮偄偰峫偊傞乮偨偩偟丄俠偺埵抲偼忬懺嘦偲摨偠偱偁傝丄墶慄偼抧暯慄偱偁傞乯丅
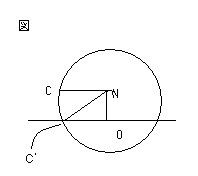
惎俠偑倣帪娫屻偵抧暯慄偵捑傓偲偒丄偦偺埵抲偼俠乫偱偁傞偐傜丄佢俶俠乫俷亖兤丂偲偡傞偲
丂丂sin兤 = 俠乫俶乛俶俷
俠乫俶偼敿宎偱偁傞偐傜丂sin兤 = (a/併2) /併2 a = 1/2
丂丂亪 兤=30亱
俠俶//俠乫俷丂偱偁傞偐傜嶖妏傛傝丂佢俠俶俠乫亖佢俶俠乫俷亖俁侽亱
傛偭偰丄惎俠偼俁侽亱夞揮偟偨偲偒抧暯慄偵捑傓丅
傛偭偰 倣*侾俆亖俁侽丂丂亪倣亖俀丂乮擇帪娫屻偵捑傓乯乧嘊
(2),(3)傛傝丂屵屻俇帪俁侽暘偐傜俆帪娫屻偵惎俠偼抧暯慄偵捑傓偺偱
惎俠偺捑傫偩帪崗偼丄丂屵屻侾侾帪俁侽暘丂偱偁傞丂//
夝摎丒偦偺17
乮儁儞僱亅儉丗岼偺柌乯
* B偲C傪媡偵偟偰峫偊偰偔偩偝偄丅
戣堄傛傝AB=BC=CN亖1偲偡傞偲丄壓婰偺恾偑昤偗傞丅
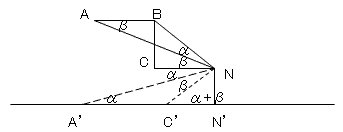
崱丄A丄C奺乆偺抧暯慄偵捑傫偩埵抲傪A乫,C乫偲偟丄佢A乪傪兛丄佢C乫NN乫傪兝偲偡傞偲丄
佢NC乫N乫偼兛+兝偲側傞丅
偙傟偼C偑捑傓傑偱偵摦偄偨妏搙偱偁傞偐傜丄摨帪崗偵捑傫偩A偵偮偄偰偺堏摦妏ANN乫傕兛+兝偲側傞丅
枖丄仮NC乫A乫偲仮NAB偼崌摨偱偁傞丅乮佹AN=NA乫丄AB=NC乫丄佢NAB亖佢A乫NC乫傛傝擇曈嫴妏偑摍偟偄乯
懄偪佢ANB亖兛偲側傞丅偙傟傛傝佢BNC亖45亱亖兛+兝偲側傞丅
場偭偰丄A偲C偼屵屻6帪30暘偐傜3帪娫屻乮15亱偱1帪娫乯偵捑傫偩偙偲偵側傞丅
師偵B偵偮偄偰峫偊傞偲丄屵屻9帪30暘偺埵抲偼C偱偁傞丅
偙偺B偺捑傫偩埵抲傪B乫偲偡傞偲
NB乫亖併2丄枖NN乫亖1/併2亖併2/2偱偁傞偐傜丄NB乫丗 NN乫亖2丗1偺捈妏嶰妏宍丅
場偭偰係丄仮NB乫N乫偵偍偄偰佢B乫亖30亱偱偁傞帠偑暘偐傞丅
30亱偼2帪娫偱偁傞偺偱B偼A,C傛傝2帪娫抶傟偰捑傫偩偙偲偵側傞丅
懄偪丄媮傔傞傕偺偼屵屻11帪30暘偱偁傞丅
夝摎丒偦偺18
乮儁儞僱亅儉丗falcon@拞妛嫵巘乯
屵屻11帪30暘
亙峫偊曽亜
仮NCB偼NB亖BC亖CA 丄佢ACB亖佢NBC亖俋侽亱傛傝丄仮ABC偲崌摨側捈妏擇摍曈嶰妏宍偲傢偐傞丅
N傛傝抧暯慄偵悅慄ND傪壓傠偡偲丄惎A偲惎B偑摨帪偵抧暯慄偵捑傓偲偒丄惎偺埵抲娭學偼恾侾偺傛偆偵側傞丅
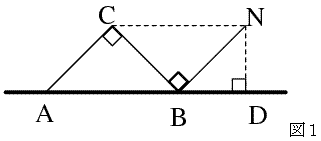
佢CNB亖係俆亱側偺偱丄曈NB偵拲栚偡傞偲恾侾偼屵屻6帪30暘偺恾傛傝係俆亱夞揮偟偨恾偲傢偐傞丅
曈ND偺挿偝傪 偲偍偔偲丄仮NBD丄仮NCB偼捈妏擇摍曈嶰妏宍偱偁傞偺偱丄NB亖併俀 倶丄NC亖俀倶 偲側傞丅
偝傜偵惎C偑抧暯慄偵捑傓偲偒丄C偺忋曽偵佢NEC亖俋侽亱偲側傞傛偆偵E傪偲傞偲丄惎偺埵抲娭學偼恾俀偺傛偆偵側傞丅
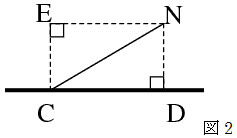
偙偺偲偒丄EC亖ND亖 偱偁傞偺偱丄 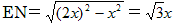 偲側傞丅
偲側傞丅
傛偭偰丄EC丗NC丗EN亖侾丗俀丗併俁 偲側傞偺偱丄佢ENC亖俁侽亱偲傢偐傞丅
偟偨偑偭偰丄曈NC偵拲栚偡傞偲恾俀偼恾侾傛傝俁侽亱夞揮偟偨恾偱偁傞偺偱丄屵屻俇帪俁侽暘傛傝俈俆亱夞揮偟偨恾偲偄偆偙偲偵側傞丅
惎偼俀係帪娫偐偗偰侾廃偡傞偺偱俈俆亱夞揮偡傞偨傔偵偼丄俀係亊俈俆亐俁俇侽亖俆帪娫偺宱夁偑昁梫丅
偟偨偑偭偰丄惎C偑捑傫偩帪娫偼丄屵屻俇帪俁侽暘傛傝俆帪娫屻偺屵屻侾侾帪俁侽暘丅
夝摎丒偦偺19
乮儁儞僱亅儉丗揮埵斀墳乯
惎俠偲惎俶傪寢傫偱偱偒傞巐妏宍俙俛俶俠偼暯峴巐曈宍偱偁傝丄
惎俙丆俛偑摨帪偵抧暯慄偵捑傓帪偺恾偼壓婰偺捠傝丅
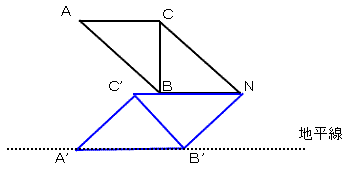
惎嵗偼俀係帪娫偐偗偰侾廃偡傞偺偱丄
丂丂俁俇侽亱乛俀係帪娫亖侾俆亱乛帪娫
惎俙丆俛偑摨帪偵抧暯慄偵捑傓偺偼丄佢俛'俶俠'亖係俆亱側偺偱
丂丂係俆亱乛侾俆亱亖俁帪娫屻
惎俠偑抧暯慄偵捑傫偩偲偒偺恾偼壓婰偺捠傝丅
俠'丄俶偐傜抧暯慄傊壓傠偟偨悅慄偲偺岎揰傪偦傟偧傟俹丄俻偲偡傞丅
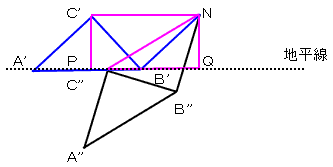
俠'俶亖俠''俶丂(俶傪拞怱偲偡傞夞揮墌偺敿宎側偺偱)
丂丂俶俻亖俠'俹丂(仮俙'俠'俹佭仮俛'俶俻側偺偱)
丂丂俠'俹亖侾乛俀俙'俛'亖侾乛俀俠'俶
丂亪俶俻亖侾乛俀俠''俶丂
傛偭偰丄仮俠''俶俻偼丄佢C''俶俻亖俇侽亱丄佢俶C''俻亖30亱偺捈妏嶰妏宍
丂亪佢俠'俶俠''亖俁侽亱
丂丂俁侽亱乛侾俆亱亖俀帪娫
傛偭偰丄惎俠偑捑傓偺偼俁亄俀亖俆丂帪娫屻偺屵屻侾侾帪俁侽暘
夝摎丒偦偺20
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
仮ABC偼捈妏擇摍曈嶰妏宍偱偡丅
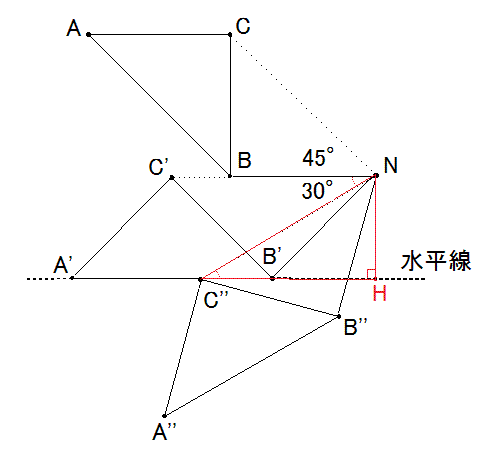
惎A丄B偑抧暯慄偵捑傓偲偒偺條巕傪A'丄B'偱偁傜傢偟傑偡丅
偙偺偲偒仮ABC丄仮A'B'C'丄仮CBN丄仮C'B'N偼傒側崌摨偱偡丅
偩偐傜丄佢BNC亖係俆亱偱偡丅
惎C偑悈暯慄偵捑傓偲偒偺條巕傪C''偱偁傜傢偟傑偡丅
N偐傜悈暯慄偵壓傠偟偨悅慄偺懌傪H偲偟傑偡丅
捈妏嶰妏宍NC''H偵偍偄偰丄NH偺挿偝傪侾乮捈妏擇摍曈嶰妏宍ABC偺幬曈偺敿暘乯偲偡傞偲丄
幬曈偺NC''偼俀乮捈妏擇摍曈嶰妏宍偺幬曈乯偵側傝傑偡丅
偡傞偲丄僺僞僑儔僗偺掕棟傛傝丄C''H偺挿偝偼丂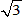 丂偵側傝傑偡丅
丂偵側傝傑偡丅
偮傑傝丄佢NC''H亖俁侽亱偱偡丅乮侾丗俀丗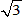 偺捈妏嶰妏宍乯
偺捈妏嶰妏宍乯
傛偭偰丄佢BNC''亖俁侽亱偱偡丅乮暯峴慄偺嶖妎乯
埲忋偐傜丄佢CNC''亖俈俆亱偱偡丅
惎偼俀係帪娫偐偗偰俁俇侽亱夞傞偺偱丄
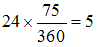 丂帪娫宱夁偟偰偄傑偡丅
丂帪娫宱夁偟偰偄傑偡丅
傛偭偰丄帪崗偼屵屻11帪俁侽暘偱偡丅
惓夝幰
| falcon@拞妛嫵巘 | 僗儌乕僋儅儞 | 棔偺嬻 |
| namiusagi | 嵞弌敪 | 偺偭偙傫 |
| 僔儏儗乕僨傿儞僈乕偺嶰栄擫 | 岼偺柌 | haya |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | AND | 忨偺偍偠偝傫 |
| 僆儎僕 | 傗側偣 | 柪巕偺梇擫 |
| 儅僆 | 揮埵斀墳 | 偙偨偮 |
| 嶰妏掕婯 | 僶儖僞儞惎恖 |
僐儊儞僩
惎俠偑悈暯慄偵捑傓傑偱偵偼丄杒嬌惎俶傪拞怱偵俈俆亱夞揮偡傞昁梫偑偁傝丄
偙傟偵偼俆帪娫偐偐傝傑偡偺偱丄侾侾帪俁侽暘偲側傝傑偡丅
抧媴偼丄栺俀係帪娫傪偐偗偰帺揮偟偰偄傑偡偺偱丄侾帪娫偁偨傝侾俆亱偺夞揮偲偄偆偙偲偵側傝傑偡丅
乮帪嵎傕偙傟偵墳偠偰惗偠傑偡偐傜丄宱搙侾俆亱偵懳偟偰丄帪嵎偼侾帪娫偱偡偹丅乯
嵟嬤偼栭嬻傪尒忋偘傞偙偲傕彮側偔側傝傑偟偨偑丄搤偺嬻偼悷傫偱偄偰惎偑尒傗偡偄
偺偱丄偨傑偵偼惎偺娤嶡傕偄偄偱偡偹丅
 top
top