栤戣155丂奼戝僐僺乕偺栤戣
101% 偐傜 1% 偛偲偵 199% 傑偱奼戝偱偒傞僐僺乕婡偑偁傝傑偡丅
偙偺僐僺乕婡傪俀夞巊偭偰偁傞尨峞傪偪傚偆偳 200% 偵奼戝偡傞曽朄傪媮傔偰偔偩偝偄丅
栤戣偺弌揟
嶼悢僆儕儞僺僢僋偵挧愴
嶼悢僆儕儞僺僢僋埾堳夛曇
島択幮僽儖乕僶僢僋僗
2005擭僩儔僀儎儖栤戣
摎偊偲夝愢
夝摎丒偦偺1
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊偼丂侾夞栚丂侾俀俆亾仺俀夞栚丂侾俇侽亾仺俀侽侽亾丂枖偼
侾夞栚丂侾俇侽亾仺俀夞栚丂侾俀俆亾仺俀侽侽亾丂偱偡丅
俙乛侾侽侽仏俛乛侾侽侽亖俀侽侽乛侾侽侽偺忦審傪廩偨偡俙丆俛乮惍悢乯傪
俠俙俽俬俷丂俥倃亅俉俈侽俹丄俥倃亅俉俋侽俹丂偱丂僾儘僌儔儉傪嶌傝寁嶼偟傑偟偨丅
俁侽峴乣俉侽峴偺僾儘僌儔儉偵傛傝
乮侾俋俋亅侾侽侾亄侾乯亊乮侾俋俋亅侾侽侾亄侾乯亖俋俋亊俋俋亖俋俉侽侾夞
偺儖乕僾偵傛傝寁嶼偟摎偊傪弌偟傑偟偨丅係暘係侽昩乮俀俉侽昩乯側偺偱1昩娫丄
栺俁俆夞寁嶼偟偰偄傞偙偲偵側傝傑偡丅僾儘僌儔儉偼師偺捠傝偱偡丅
侾侽丏俢俬俵丂俢乮俀乯丆俤乮俀乯 俀侽丏俹俼俬俶俿乬俲俙俲倀俢俙俬乭丗俥亖侾 俁侽丏俬俥丂俬俶俲俤倄亹亖乬乭俿俫俤俶丂俁侽 係侽丏俥俷俼丂俙亖侾侽侾丂俿俷丂侾俋俋 俆侽丏俥俷俼丂俛亖侾侽侾丂俿俷丂侾俋俋 俇侽丏俠亖俙仏俛 俈侽丏俬俥丂俠亖俀侽侽侽侽丂俿俫俤俶丂俢乮俥乯亖俙丗俤乮俥乯亖俛丗俥亖俥亄侾 俉侽丏俶俤倃俿丂俛 俋侽丏俶俤倃俿丂俙 侾侽侽丏俛俤俤俹丂侾 侾侾侽丏俥俷俼丂俧亖侾丂俿俷丂俥亅侾 侾俀侽丏俹俼俬俶俿乬俙乭丟俧丟乬亖乭丟俢乮俧乯丟乬亾丂仌丂俛乭丟俧丟乬亖乭丟俤乮俧乯丟乬亾乭 侾俁侽丏俶俤倃俿丂俧 侾係侽丏俬俥丂俬俶俲俤倄亹亖乬乭丂俿俫俤俶丂侾係侽 侾俆侽丏俠俴俽丗俧俷俿俷丂俀侽
僾儘僌儔儉偺愢柧
侾侽峴偺俢乮俀乯丄俤乮俀乯偼摎偊偑俀屄偁傞偙偲偑暘偐傝傑偟偨偺偱曄悢傪乮俀乯偲偟傑偟偨丅
俀侽峴偱俲俙俲倀俢俙俬偲昞帵偝傟偨傜俤倃俤僉乕傪墴偟傑偡丅
侾侽侽峴偺俛俤俤俹壒偑柭傝侾俀侽峴偱師偺傛偆偵僨傿僗僾儗僀偵摎偊偑昞帵偝傟傑偡丅
丂丂丂俙乮侾乯亖侾俀俆亾丂仌丂俛乮侾乯亖侾俇侽亾
丂丂丂俙乮俀乯亖侾俇侽亾丂仌丂俛乮俀乯亖侾俀俆亾
偦偺娫俀俉侽昩偱偡丅僄僋僙儖摍偱嶌傞儐乕僓乕僼僅乕儉偺Visual Basic側傜弖娫偵
摎偊偑弌傑偡丅
夝摎丒偦偺2
乮儁儞僱亅儉丗昹揷丂柧枻乯
僄僋僙儖偺儅僋儘偱夝偒傑偟偨丅暋悢慻偺摎偑弌偰棃偰傕懳墳弌棃傞傛偆偵偟偰偁傝傑偡丅
侾俀俆亾偲侾俇侽亾偱僐僺乕偡傟偽偄偄偱偡丅
摨偠奼戝棪偲偡傞偲丄挷榓暯嬒偺偄偄椺偲側傝傑偡丅偮傑傝丄侾侽侽併俀亾佮侾係侾亾偱偡偹丅
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Dim n1 As Long
Dim n2 As Long
For n1 = 101 To 199
For n2 = n1 To 199
If n1 * n2 = 20000 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = n1
Cells(Cells(1, 1).Value, 3).Value = n2
End If
Next n2
Next n1
End Sub
夝摎丒偦偺3
乮儁儞僱亅儉丗恀壞偺僒儞僞乯
侾俀俆僷乕僙儞僩亊侾俇侽僷乕僙儞僩亖俀侽侽僷乕僙儞僩 偱偡丅
俀侽侽亖侾俇亊侾俀丏俆偵偟偰偐傜侾俇偲侾俀丏俆傪侾侽偱妱傞偺偑傢偐傝傗偡偄偲巚偄傑偟偨丅
夝摎丒偦偺4
乮儁儞僱亅儉丗僆儎僕乯
侽丏侽侾亝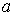 ,
,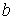 亝侽丏俋俋
亝侽丏俋俋
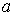 亝丂
亝丂
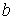 扐偟
扐偟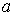 ,
, 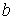 偼侽丏侽侾崗傒丂丒丒丒(1)
偼侽丏侽侾崗傒丂丒丒丒(1)
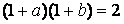 傛傝
傛傝
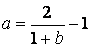
傑偨丂(1)傛傝丂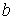 亞
亞
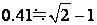
偙偙偱,丂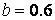 偲偡傞偲丂
偲偡傞偲丂
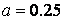
亪丂侾俀俆亾丂偲丂侾俇侽亾丂偺俀夞
夝摎丒偦偺5
乮儁儞僱亅儉丗namiusagi乯
堦夞栚偺奼戝棪傪X(1.01乣1.99)偲偟丄擇夞栚偺奼戝棪傪Y偲偟偰丄
Y=2亐X偺彜偑彫悢揰2寘枠偱妱愗傟傟偽偦傟偑摎偲側傞丅
奼戝棪(X丄Y)偺彫悢揰埲壓2寘栚偺偳偪傜偐偑0偐5側偺偱X=(21乣39)/20=m/20丄Y=(21乣39)=n/20偲偟偰丄
XY=mn/400=2偱丄mn=800偲側傝丄800偺栺悢偺偆偪21偐傜39偺娫偵偁傞偺偼32,25偺2屄偱晇乆偑m偲n偵側傞丅
X=25/20=1.25丄Y=32/20=1.6傕偟偔偼X=1.6丄Y=1.25
屘偵堦夞栚偺奼戝傪125%丄擇夞栚傪160%偵偡傞偐丄媡偵堦夞栚偺奼戝傪160%丄擇夞栚傪125%偵偡傟偽椙偄丅
夝摎丒偦偺6
乮儁儞僱亅儉丗偺偭偙傫乯
俀侽侽侽侽亖俀俆丒俆係
傛偭偰俀侽侽侽侽偺栺悢偺屄悢偼俇丒俆亖俁侽乮屄乯
彫偝偄曽偐傜悢偊偰侾俆斣栚傑偱傪暲傋傞偲
侾丄俀丄係丄俆丄俉丄侾侽丄侾俇丄俀侽丄俀俆丄俁俀丄係侽丄俆侽丄俉侽丄侾侽侽丄侾俀俆
戣堄傛傝丂俀侽侽侽侽亖侾俀俆丒侾俇侽
乮摎乯侾夞栚丒丒丒侾俀俆亾丄俀夞栚丒丒丒侾俇侽亾丂乮偁傞偄偼偦偺媡乯
偄偄栤戣偱偡偹両姶怱偟傑偟偨丅
夝摎丒偦偺7
乮儁儞僱亅儉丗haya乯
亂夝摎亃
125% x 160% 偱偡丅
亂夝偒曽亃
m x n = 20000 偲側傞傛偆側 101 乣 199 偺娫偺 2 偮偺惍悢 m, n 傪媮傔傞丅
偲偙傠偱丄20000 = 25 * 54 偱偁傝栺悢偼30屄偁偭偰徃弴偵暲傋傞偲丄
1
2
4
5
8
10
16
20
25
32
40
50
80
100
125
160
200
250
400
500
625
800
1000
1250
2000
2500
4000
5000
10000
20000偲側傝丄101 乣 199 偺娫偵偁傞傕偺偼丄125 偲 160 偺 2 屄丅丂偙傟偑丄
125 * 160 = 20000 偲戣堄傪枮偨偟偰偄傞丅
夝摎丒偦偺8
乮儁儞僱亅儉丗SOU乯
a*b=20000丂側傞 a,b 傪媮傔傞丅
a 懄偪 20000/b 偑惍悢偱偁傞偙偲偐傜 b 偼 20000 偺栺悢丅
偦偺傛偆側 b 偵懳墳偡傞 a 偲偱慻傪嶌傞偲丄
忦審傪枮偨偡傕偺偼 53 偲 5*25 偲偄偆慻傒崌傢偣偺傒丅
懄偪丄125% 偲 160% 偲偄偆慻傒崌傢偣偺傒偑摎偱丄懠偵偼懚嵼偟側偄丅
夝摎丒偦偺9
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
堦弖壜擻側傫偩傠偐丒丒丒丠偭偰巚偄傑偟偨偑...姩偱丄125*160=20000 偵側傞傫偩
偲巚偄寁嶼偟偰傒傑偟偨丒丒丒
丂丂丂(1+a/100)(1+b/100)=2
丂丂丂(100+a)(100+b)=20000
丂丂丂20000=25*54
偙傟傪100戜偺3寘摨巑偺愊偵偡傟偽偄偄偺偱...
丂丂丂53=125,25*5=160
52 偩偗偩偲丄22*52=100,
23*52=200 偵側偭偰偟傑偆偺偱...側偄丅
丂丂丂54=625亜200
偗偭偒傚偔...堦堄偵寛傑傞傫偱偡偹 ^^
125%偲160%傪巊偊偽偄偄傢偗偱偡偹乮弴斣偼偳偪傜偱傕傛偄乯侓
夝摎丒偦偺10
乮儁儞僱亅儉丗柪巕偺梇擫乯
妡偗嶼偟偰暘曣偑10,000丄暘巕偑20,000偩偐傜20,000傪慺場悢暘夝偟偰丒丒
199傪挻偊側偄2偮偺惍悢偵栠偣偽偄偄偺偱丄
丂20000
=5*10*5*10*2*2*2
=5*5*5*5*2*2*2*2*2
=25*5*5*2*2*2*2*2
=125*5*2*2*2*2*2
=125*10*2*2*2*2
=125*160
摎丗125%偲160%
夝摎丒偦偺11
乮儁儞僱亅儉丗儅僆乯
夝摎丗160%偱僐僺乕偟偨屻丄125亾偱僐僺乕偡傞乮枖偼偦偺媡乯丅
侾夞栚偺僐僺乕偺攞棪傪x % , 俀夞栚偺攞棪傪y % 偲偡傞丅
丂丂丂1 亊 x/100 亊 y/100 = 2
傛傝丄xy = 20000
塃曈傪場悢暘夝偟偰丄
丂丂丂xy = 25 亊 54
101 亝 x 亝 199丄101 亝 y 亝 199
傛傝丄x亜y偺偲偒
丂丂丂x=25 亊 5 = 160丄y=53 = 125
偙傟傛傝丄160%偱僐僺乕偟偨屻丄125亾偱僐僺乕乮枖偼偦偺媡乯偡傟偽丄
俀夞偺僐僺乕偱200亾偵偱偒傞丅
夝摎丒偦偺12
乮儁儞僱亅儉丗嵞弌敪乯
20000=25*54
101埲忋199埲壓偺愊偵曄宍偟偰
丂丂20000=125*160
偲偄偆偙偲偱丄
125%偲160%傪偮偐偆丅丒丒丒乮摎乯
夝摎丒偦偺13
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
摎偊
侾俀俆亾偲侾俇侽亾乮媡弴偲偁傢偣俀捠傝乯
峫偊曽
梫偼妡偗偰侾侽侾乣侾俋俋偺俀悢傪偐偗偰俀侽侽侽侽偵偡傟偽椙偄丅
傑偢偼慺場悢暘夝丅俀5亊俆4
俆偺係忔偼俇俀俆側偺偱丄俆偺晹暘偼俀俆偲俀俆偁傞偄偼俆偲侾俀俆
俀俆偺応崌偼係攞偱侾侽侽丆俉攞偱俀侽侽偲側傞偺偱晄揔丅
備偊偵桞堦夝偼丄侾俀俆偲侾俇侽乮亖俆亊俁俀乯
夝摎丒偦偺14
乮儁儞僱亅儉丗挿嶈搰尨丂偐偑傒乯
俀侽侽亾傪俀侽侽侽侽偲峫偊傞丅
椺偊偽丂侾俀侽亾亊侾俇侽亾亖侾俋俀侽侽偲峫偊傞丅
偙偺偲偒丄戣堄傪枮偨偡偵偼丄俀侽侽侽侽偵側傟偽傛偄丅
俀侽侽侽侽亖俀俆亊俆係 偩偐傜
俀俆偺栺悢偲俆係偺栺悢偺慻崌偣傪峫偊偰丄
乷侾丆俀侾丆俀俀丆俀俁丆俀係丆俀俆乸偲乷侾丆俆侾丆俆俀丆俆俁丆俆係乸偺梫慺偺妡偗崌傢偣偺拞偱丄俀侽侽侽侽偵側傞偺偼
俆俁 亊乮俀俆亊俆乯偺慻崌偣偩偗偱偁傞丅
偡側傢偪丄侾俀俆亊侾俇侽亖俀侽侽侽侽
偟偨偑偭偰丄侾俀俆亾偲侾俇侽亾乮弴晄摨乯偺奼戝僐僺乕傪侾夞偢偮偡傟偽傛偄丅
亂摎亃丂侾俀俆亾偲侾俇侽亾
夝摎丒偦偺15
乮儁儞僱亅儉丗僇儕僆僇乯
125%亊160%丂偱丂200%偱偡丅
a/100亊b/100=2=20000/10000側偺偱丄101亝a,b亝199偱愊偑20000偵側傞20000偺栺悢
a,b偺慻崌傢偣傪媮傔傟偽傛偄丅
20000=25亊54偱偁傞偙偲偐傜奩摉偡傞傕偺傪扵
偡偲53亊(5亊25)懄偪125亊160偑偙傟偵摉偰偼傑傞丅
夝摎丒偦偺16
乮儁儞僱亅儉丗AND乯
傑偢丄栤戣傪埲壓偺傛偆側摨摍偺栤戣偵抲偒姺偊偰峫偊偰傒傑偟偨丅
亂栤戣侾俆俆偲摨摍偺栤戣亃
侾侽侽傛傝戝偒偔俀侽侽枹枮偺惍悢丄X偲Y偲偺愊偑20,000偲側傞X偲Y偺慻崌偣傪慡偰媮傔傛丅
仧夝朄
傑偢丄20,000傪慺場悢暘夝偟偰傒傑偟偨丅
20,000亖25 * 54 = 32 * 625
俁俀偼侾侽侽傛傝彫偝偔丄俇俀俆偼俀侽侽傛傝戝偒偄偨傔丄
俁俀仏俆丂偲丂俇俀俆亐俆丂傪帋偡偲丄侾俇侽偲侾俀俆偲側傝丄
忦審偵偁偆偙偲偑暘偐傞丅
師偵丄侾俇侽偲侾俀俆傪婎弨偲偟偰丄偦偺嬤朤偺夝偺慻崌偣傪
帋偟偰傒傞偑丄偄偢傟傕侾侽侽埲壓偐丄200埲忋偲側傞偨傔丄
忋婰偺侾俇侽偲侾俀俆偑桞堦偺慻崌偣偲側傞丅
夝摎丒偦偺17
乮儁儞僱亅儉丗嶰妏掕婯乯
戣堄傛傝丆兛丆兝傪 1亝兛丆兝亙100 偺惍悢偲偟偰丆
丂丂丂丂(1亄兛/100)(1亄兝/100)亖2丂亪 (100亄兛)(100亄兝)亖20,000亖25丒54
偑惉傝棫偮丅
100亄兛丆100亄兝 偼 20,000 偺栺悢偱丆偦傟偧傟 101 埲忋丆200 枹枮偩偐傜
丂丂丂丂100亄兛亖53亖125丆100亄兝亖25丒5亖160丂乮傑偨偼丆偙偺媡乯
傛偭偰丆200亾奼戝偡傞偵偼丆125亾 偲 160亾 偺奼戝傪峴偆丅媡偱傕傛偄丅乧乵摎乶
夝摎丒偦偺18
乮儁儞僱亅儉丗falcon@拞妛嫵巘乯
亙摎偊亜
弴斣偼娭學側偔125亾丄160亾傪1夞偢偮峴偆丅
亙峫偊曽亜
200亾偼丄挿偝傪2攞偵偡傞偲偄偆堄枴側偺偱
1夞栚偺僐僺乕偱a攞丄2夞栚偺僐僺乕偱b攞偵偡傞丄偲暥帤傪抲偔偲
丂丂a亊b亖2丂
偲偄偆幃偑摼傜傟傞丅
a攞佁100a 亾丄丂b攞佁100b 亾偲偄偆懳墳偱偁傞偺偱忋婰偺幃偐傜
丂丂100a亊100b亖20000丂
偲偄偆幃偑摼傜傟傞丅
100a丄100b偼偦傟偧傟乽101埲忋199埲壓偺惍悢乿偱偁傞偺偱
乽偐偗偰20000偲側傞昐偺埵偑侾偱偁傞嶰寘偺俀偮偺惍悢偺慻乿傪偝偑偣偽傛偄丅
20000傪慺場悢暘夝偡傞偲丄25 亊 54 偱偁傞偺偱丄忦審偵崌偆慻傒崌傢偣傪扵偡偲丄
53 亖 125丄丂25 亊 5 亖160偺慻傒崌傢偣偺偲偒丄
125亊160亖20000偲側傝丄偆傑偔偄偔丅
偮傑傝125亾偲160亾偺慻傒崌傢偣偺偲偒偵200亾偺奼戝偑婲偒傞丅
偙偺庤弴偺弴斣偼栤傢側偄偺偱
2夞偺僐僺乕偱200亾偵奼戝偡傞偵偼
弴斣偼娭學側偔125亾丄160亾傪1夞偢偮峴偊偽傛偄丅
亙峫偊曽俀亜
俀夞偺奼戝傪廔偊偰俀侽侽亾丄偮傑傝俀攞偵偡傞偙偲偲僐僺乕婡偺攞棪偑桳棟悢偱偁傞偙偲傪峫椂偡傞偲丄
俀夞偺奼戝傪偦傟偧傟倐/倎攞丄俀倎/倐攞偲昞偣傞丅 乮倎偲倐偼屳偄偵慺側惍悢乯
攞棪偑侾丏侽侾攞乣侾丏俋俋攞偱偁傞偺偱倎亙倐亙俀倎
傑偨倐/倎丄俀倎/倐偺岓曗偼侾侽侾/侾侽侽乣侾俋俋/侾侽侽側偺偱
暘曣偱偁傞倎偲倐偺岓曗偼侾侽侽偺栺悢偵尷傜傟傞丅
乮侾侽侽偺栺悢偼侾丄俀丄係丄俆丄侾侽丄俀侽丄俀俆丄俆侽丄侾侽侽乯
偝傜偵丄倎偲倐偼屳偄偵慺偱偁傝丄倎亙倐亙俀倎偱偁傞偺偱
乮倎丆倐乯亖乮係丆俆乯偲寛傑傞丅
偮傑傝丄媮傔傞俀夞偺奼戝偼
倐/倎攞亖俆/係攞亖侾俀俆亾丄俀倎/倐攞亖俉/俆攞亖侾俇侽亾偱偁傞丅
夝摎丒偦偺19
乮儁儞僱亅儉丗teki乯
摎偊
侾俀俆亾偵奼戝屻丄侾俇侽亾偵奼戝偡傞丅乮弴晄摨乯
峫偊曽
俀侽侽侽侽侽偺栺悢偼丄俀偲俆偟偐偁傝傑偣傫丅乮俀侽侽侽侽侽亖俀俆亊俆係乯
偱丄俀偲俆偱偗巊偭偰偱偒傞侾侽侾偐傜侾俋俋偺俀悢傪媮傔傟偽偄偄傢偗偱偡丅
偐偗偰挌搙俀侽侽侽侽侽偵側傞偺偼丄侾俀俆偲侾俇侽偺俀悢偟偐偁傝傑偣傫丅
夝摎丒偦偺20
乮儁儞僱亅儉丗岼偺柌乯
1夞栚偲2夞栚偺攞棪傪奺乆A,B偲偡傞偲丄
戣堄傛傝丂丂丂A丒B亖20000丂丂丒丒丒丒丒丒(1)丂
丂丂丂丂丂丂丂101亙A,B丂亙199丂丂丒丒丒丒(2)丂丂偑惉棫偡傞丅
偲偙傠偱丄20000亖25亊54丂偱偁傞偐傜丄
(2)偺忦審傛傝戝偒偄曽偺抣偼嵟戝偱傕25亊5亖160偱偁傝丄
偙偺偲偒傕偆堦曽偼53丂亖125偲側傞丅摨條偵偟偰懠偺悢偑側偄偐妋偐傔傞偲丄
忦審(2)偑岠偄偰偍傝柍偄帠偑暘偐傞丅
場偭偰丄媮傔傞攞棪偼125亾偲160亾偱偁傞丅
夝摎丒偦偺21
乮儁儞僱亅儉丗揮埵斀墳乯
偙偺栤戣偼丄侾侽侾亝倃丆倄亝侾俋俋丂偺斖埻偵偁傞惍悢偺偆偪丄
倃倄亖俀侽侽侽侽傪枮偨偡擇偮偺栺悢傪媮傔傞偙偲偵摍偟偄丅
俀侽侽侽侽亖俀俆亊俆係丂偲慺場悢暘夝偱偒傞偺偱
俀俆亊俆亖侾俇侽丄俆俁亖侾俀俆丂偩偗偑忋婰忦審傪枮懌偡傞丅
傛偭偰丄侾俀俆亾偲侾俇侽亾偺奼戝僐僺乕傪奺堦夞偢偮峴偊偽栚揑傪払惉偱偒傞丅
夝摎丒偦偺22
乮儁儞僱亅儉丗T_Tatekawa乯
2夞巊偭偰200%偵偡傞偺偱丆1AB % 偲 1CD % (A, B, C, D 偼 0-9 偺悢帤) 傪
慻傒崌傢偣偰丆200.00% 偵偡傞帠傪峫偊傑偡丏
20000 傪慺場悢暘夝偡傞偲丆
丂丂丂20000 = 2x2x2x2x2 x 5x5x5x5
偱偡丏偙偙偐傜 100 傛傝戝偒偔 200 傛傝彫偝偄 20000 偺栺悢傪峫偊傞偲丆
125 偲 160 偟偐偁傝傑偣傫丏
丂丂丂125 x 160 = 20000
側偺偱丆僐僺乕偼 125% 偲 160% 傪孞傝曉偣偽 200% 偵奼戝偱偒傑偡丏
夝摎丒偦偺23
乮儁儞僱亅儉丗僔儏儗乕僨傿儞僈乕偺嶰栄擫乯
尨峞偺奼戝棪偺扨埵傪亾偲偟丄1夞栚丒2夞栚偦傟偧傟偺奼戝棪傪a,b偲偍偔丅
戣堄傛傝a,b偺忦審偼丄
丂丂101亝 a,b 亝199丂(a,b偼惍悢)丂丒丒丒乮仏乯
偱偁傞丅
傕偲偺尨峞偺戝偒偝傪俽偲偍偔偲丄1夞栚偺僐僺乕偱偼(a/100)亊俽偲奼戝偝傟丄
2夞栚偺僐僺乕偱尨峞偼乷乮a/100乯亊俽乸(b/100)偺戝偒偝偲側傞丅
偙傟偑尦偺尨峞偺200亾偺戝偒偝偱偁傞偙偲偐傜丄
丂丂乮a/100乯(b/100)亊S亖乮200/100乯亊俽丂丒丒丒(1)
偑惉傝棫偮丅嘆偺椉曈偵10000傪偐偗傞偙偲偱
丂丂a亊b亖20000丂丒丒丒(2)
傪摼偰丄(2)偍傛傃忦審乮仏乯傪枮偨偡a,b偑夝偲側傞丅偝偰丄
丂丂20000亖25亊54丂丒丒丒(3)
偲慺場悢暘夝偱偒傞偺偱丄0亝m亝5, 0亝n亝4側傞惍悢m,n傪梡偄偰丄(a,b)偺慻偼
丂丂乮a,b乯亖乮2m亊5n, 25-m亊54-n乯丂丒丒丒(4)
偲彂偒壓偡偙偲偑偱偒傞丅
偙偙偱丄(4)偵懳偟n偵偮偄偰応崌暘偗傪峴偄丄忦審乮仏乯傪枮偨偡慻傪挷傋傞丅
(鶣乯n亖0偺偲偒
丂丂乮a,b乯亖{2m, 25-m亊54}
偲側傞偑丄m偺偲傝摼傞慡偰偺抣偵偍偄偰丄25-m亊54亖25-m亊625亜199側偺偱晄揔丅
(鶤乯n亖1偺偲偒
丂丂乮a,b乯亖乷2m亊5, 25-m亊53乸
0亝m亝4偺応崌丄25亙101側偺偱晄揔丅
m亖5偺応崌丄(a,b)亖乮160,125乯丂偲側偭偰忦審傪枮偨偡丅
(鶥乯n亖2偺偲偒
丂丂乮a,b乯亖乷2m亊52, 25-m亊52乸
m亖0偺応崌丄a亖25亙101偲側傞偺偱晄揔丅
m亖1,2,3,4偺応崌丄2m亊52亙101側偺偱晄揔丅
m亖5偺応崌丄b亖25亙101偲側傞偺偱晄揔丅
(鶦)n亖3偺偲偒
丂丂乮a,b乯亖乷2m亊53, 25-m亊5乸
m亖0偺応崌丄(a,b)亖乮125,160乯偲側偭偰忦審傪枮偨偡丅
1亝m亝5偺応崌丄2m亊53亖2m亊125亜199側偺偱晄揔丅
(鶧乯n亖4偺偲偒
丂丂(a,b乯亖乷2m亊54, 25-m乸
偲側傞偑丄m偺偲傝摼傞慡偰偺抣偵偍偄偰丄2m亊54亖2m亊625亜199側偺偱晄揔丅
埲忋傛傝丄嘇偍傛傃忦審乮仏乯傪枮偨偡(a,b)偺慻
丂丂(a,b)亖乮125, 160乯, (160, 125)
傪夝偲偟偰摼傞丅
夝摎丒偦偺24
乮儁儞僱亅儉丗棔偺嬻乯
擇偮偺攞棪傪偦傟偧傟倶丆倷(%)乮偦傟偧傟帺慠悢乯偲偡傞偲丄
(x/100)丒(y/100)=200/100
丂丂丂丂丂丂亪xy=20000
=25丒54
偙偺偲偒丄攞棪x偵偮偄偰峫偊傞偲
x偼 101亝x亝199 乮乧(1)乯 偺斖埻偺帺慠悢偱偁傞偐傜
帺慠悢倣丆値乮1亝m亝5,1亝n亝4乯傪梡偄偰
x=2m丒5n丂丂偲昞偣傞丅
偙偺偲偒(1)傪枮偨偡(m,n)偺慻傒崌傢偣傪峫偊傞丅
[1] n=0丂偺偲偒丂丂101亝2m亝199 傪枮偨偡m偺抣偼
丂25=32亙101丂傛傝懚嵼偟側偄丅
[2] n=1丂偺偲偒丂101/5(=20,2)亝2m亝199/5(=39,8) 傪枮偨偡m偺抣偼
丂24=16 , 25=32丂丂傛傝丂m=5
[3] n=2丂偺偲偒丂101/25(=4,04)亝2m亝199/25(=7,96) 傪枮偨偡m偺抣偼
丂22=4 , 23=8丂丂 傛傝懚嵼偟側偄丅
[4] n=3丂偺偲偒丂101/125(=0,808)亝2m亝199/125(=1,592) 傪枮偨偡m偺抣偼
丂20=1 , 21=2丂丂 傛傝m=0
[5] n=4丂偺偲偒丂x=625丂傛傝晄揔丅
傛偭偰丄嘆傪枮偨偡(m,n)偺慻傒崌傢偣偼
(m,n) = (5, 1) 乧(2)丂, (0, 3) 乧(3)
丂(2)偺偲偒丄 x=25丒51 =160
丂丂傑偨丄丂 y=20000/160 =125
丂(3)偺偲偒丄 x=20丒53 =125
丂丂傑偨丄丂 y=20000/125 =160
傛偭偰丄擇夞偺奼戝偱尦偺尨峞偺戝偒偝傪擇攞偵偡傞傛偆側奼戝偺巇曽偼
丂125%佀160%丂 傕偟偔偼丂丂160%佀125%丂丂偺擇捠傝偱偁傞丅
夝摎丒偦偺25
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
侾侽侾偐傜侾俋俋偺斖埻偺俀惍悢偺愊偑丄俀侽侽侽侽偵側傟偽傛偄偙偲偵側傝傑偡丅
俀侽侽侽侽亖俀亊俀亊俀亊俀亊俀亊俆亊俆亊俆亊俆偲慺場悢暘夝偝傟傑偡丅
俆偺暘偗曽偼丄(1)係屄偲侽屄丄(2)俁屄偲侾屄丄(3)俀屄偲俀屄偺俁捠傝偱偡丅
(1)偺俆偑係屄偺応崌丄愊偼俇俀俆偱偡丅
偙傟偼侾侽侾偐傜侾俋俋偵擖傜側偄偺偱丄忦審偵崌偄傑偣傫丅
(3)偺俆偑俀屄偺応崌丄愊偼俀俆偱偡丅
巆傝偺場悢偼俀偩偗側偺偱丄俀俆亊俀亊俀亖侾侽侽丄俀俆亊俀亊俀亊俀亖俀侽侽偲側傝侾侽侾偐傜侾俋俋偵廂傑傞傛偆偵偼偱偒傑偣傫丅
(2)偺俆偑俁屄偺応崌丄愊偼侾俀俆偱偡丅
巆傝偺場悢偺愊俀亊俀亊俀亊俀亊俀亊俆亖侾俇侽偱偡丅
(2)偺応崌偆傑偔偄偔椺偑尒偮偐傝傑偟偨丅
偙偺懠偵偼椺偑側偄偙偲偑師偺傛偆偵峫偊傞偲愢柧偱偒傑偡丅
俆傪擖傟懼偊偰傕偆傑偔偄偒傑偣傫丅
(2)偺忬懺偐傜俆偺傗傝偲傝傪偡傞偲丄(1)偐(3)偺応崌偵側傝傑偡偑丄偲傕偵偆傑偔偄偐側偄偙偲偑暘偐偭偰偄傑偡丅
侾俀俆偵俀傪偐偗傞偲侾俋俋傪挻偊偆傑偔偄偒傑偣傫丅
埲忋偐傜丄侾俀俆攞丄侾俇侽攞乮媡傕壜乯偲僐僺乕傪偡傟偽偆傑偔偄偒傑偡丅
惓夝幰
| namiusagi | 僆儎僕 | 僗儌乕僋儅儞 |
| falcon@拞妛嫵巘 | 嵞弌敪 | 岼偺柌 |
| 偺偭偙傫 | haya | 儅僆 |
| teki | 揮埵斀墳 | 僶儖僞儞惎恖 |
| 柪巕偺梇擫 | 昹揷柧枻 | 忨偺偍偠偝傫 |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | 僇儕僆僇 | 挿嶈搰尨丂偐偑傒 |
| 僔儏儗乕僨傿儞僈乕偺嶰栄擫 | 棔偺嬻 | AND |
| T_Tatekawa | SOU | 恀壞偺僒儞僞 |
| 嶰妏掕婯 |
僐儊儞僩
偙偺栤戣偼丄愊偑20000偵側傞俀偮偺惍悢偺慻崌偣傪扵偟偰偔傞偲偄偆偙偲偵側傝傑偡丅
懡偔偺曽偑慺場悢暘夝傪庤妡偐傝偵扵偟偰偔偩偝偄傑偟偨丅
奼戝棪200%(俀攞)偲偄偆偺偼丄憡帡斾(挿偝偺斾乯偱偡偐傜丄柺愊斾偱偄偆偲係攞偲偄偆偙偲偵側傝傑偡丅
堦斒揑側僐僺乕婡偱偼丄乽俙係仺俙俁乿丄乽俛俆仺俛係乿偲偄偆柺愊偑俀攞偵側傞奼戝偑儊僯儏乕偵偁傞偲巚偄傑偡丅
偙傟偼柺愊斾俀攞偱偡偐傜丄憡帡斾(挿偝偺斾乯併俀攞偺奼戝傪峴偭偰偄傞偙偲偵側傝傑偡丅
偙傟傪俀夞孞傝曉偣偽丄憡帡斾(挿偝偺斾乯俀攞丄柺愊斾係攞偲側傝傑偡丅
尰幚揑偵偼偙偆偡傞偺偱偟傚偆偑丄崱夞偼丄
惍悢奼戝偟偐偱偒側偄僐僺乕婡傪巊偭偰偍摎偊偄偨偩偒傑偟偨偺偱丄偙傟偼偩傔偱偡偹丅
 top
top