問題154　正十二角形の問題

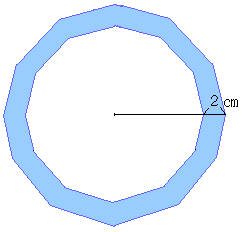図のように、同じ中心を持ち、半径の差が２cmの２つの円の内側にそれぞれ接する正十二角形があります。両者に挟まれたブルーの部分の面積が2004cm^２のとき、小さい方の円の半径を求めてください。

問題の出典

算数オリンピックに挑戦
算数オリンピック委員会編
講談社ブルーバックス
2004年ファイナル問題
(出題：般若尚之)

答えと解説

解答・その1

（ペンネ－ム：松本峻典）

答えは１６６ｃｍです。
大きい正１２角形の面積は
{大きい方の半径をｘとします。｝
　　　x・(x/2)・(1/2)・12＝３x^２
半径は｛ｘ－２｝なので
内側の十二角形の面積は、｛x－２｝を代入し
　　　３・{x－２}^２
つまり
　　　３ｘ^２－３・{x－２}^２＝２００４
ｘ＝１６８

解答・その2

（ペンネ－ム：SOU）

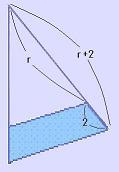
(小さい円の半径がr) 問の図形を12等分し、上図のような台形(面積167cm²)を考えると、大きな三角形の面積から小さな三角形の面積を引くことでこの台形の面積が出せますので、

　　

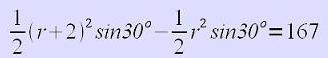
よって r=166 //

解答・その3

（ペンネ－ム：のっこん）

小さい方の円の半径： r (cm)
大きい方の円の半径： r+2 (cm)
　　　2004/12=167
(1/2)・(r+2)²・sin30°-(1/2)・r²・sin30°=167
r=166(cm)

解答・その4

（ペンネ－ム：バルタン星人）

答え
１６６ｃｍ

考え方：
内側の円の半径をＸとする。
１２角形を１２等分した、すなわち頂角が３０度の二等辺三角形で考えると、内外の差は２００４／１２＝１６７
また三角形の面積差は、Ｓｉｎ３０度が１／２なので
［（Ｘ＋２）^２－Ｘ^２］／４＝１６７
展開すると
Ｘ＋１＝１６７　　Ｘ＝１６６

＊三角形の二辺をＡ，Ｂ、挟角をθとすると△の面積は1/2Ａ・ＢSinθから面積差を計算

解答・その5

（ペンネ－ム：長崎島原　かがみ）

求める半径をｒとすると、

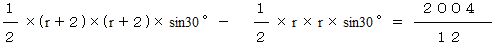
これを解いて、ｒ＝１６６㎝

解答・その6

（ペンネ－ム：namiusagi）

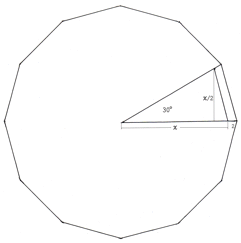
12角形の一部分を考える。
小さい方の円の半径をxとすると、大きい方の円の半径はx+2 となる。
一部分は全体の12分の1だから大小の面積の差は2004/12=167 なる。
図の角30度の三角形の面積は大きい方が{(x+2)*(x+2)/2}/2=(x+2)* (x+2)/4,
同じく三角形の面積は小さい方が(x*x/2)/2=x*x/4となる。
この面積の差が167なので(x+2)(x+2)/4-x*x/4=(4x+4)/4=x+1=167
∴ x=166cm

解答・その7

（ペンネ－ム：再出発）

１２分割されたうちの一組の二等辺三角形を考えて
ブルーの部分の面積は
　　2004/12=167
小円の半径を r とすると、
∴　{(r+2)²*sin(π/6)}/2-{r²*sin(π/6)}/2=167
これを解いて
　　r = 166 (cm)・・・（答）

解答・その8

（ペンネ－ム：オヤジ）

大きな正十二角形の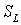面積をとし、小さな正十二角形の面積を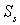とする、また小さい方の円の半径を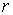とすると。題意より

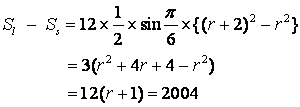
これを解いて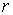＝１６６　　　
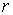　∴ ＝１６６ｃｍ

解答・その9

（ペンネ－ム：haya）

問題154 正十二角形の問題の解は 166 cm です。

【解き方】
小円の半径を r とすると、内接する12角形を構成する三角形 1 個の面積は
　　　1/2 x r² x sin(2π/12) = 1/2 x r² x 1/2 = 1/4 x r²
同様に大円では
　　　1/4 x (r + 2)²
水色の部分の面積は、両者の差の 12 倍であるから
　　　1/4 x [(r + 2)² - r²] x 12
これが 2004 cm² であるから
　　　3 x (4r + 4) = 2004
これを解いて
　　　r = 166

解答・その10

（ペンネ－ム：浜田　明巳）

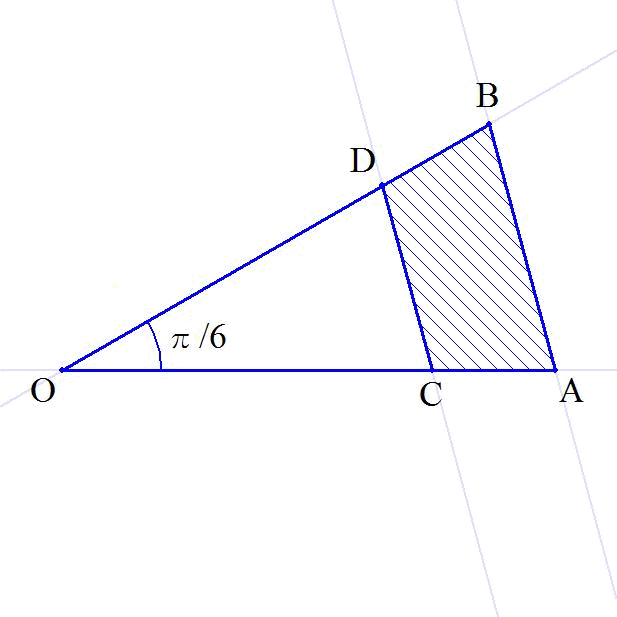
同心円の中心をＯ，外部の正十二角形の辺の１つをＡＢとし，△ＯＡＢを取り出す．その三角形内の内部の正十二角形の辺をＣＤとする．
四角形ＡＢＤＣの面積の１２倍が図のブルーの部分の面積となる．
　ＯＣ＝ＯＤ＝ｒ（cm）とすると，
　　１２×{(ｒ＋２)^２－ｒ^２}×sin(π／６)／２＝３(４ｒ＋４)＝１２(ｒ＋１)＝２００４
　　∴ｒ＋１＝１６７
　　∴ｒ＝１６６（cm）………(答)

解答・その11

（ペンネ－ム：三角定規）

半径 a の円に内接する正12角形は，図のように角度 π/12 の直角三角形を24個集めたもので，
　　　面積＝24・(1/2)acos(π/12)・asin(π/12)
　　　　　＝6a²sin(π/6)
　　　　　＝3a²
題意より
　　3(a＋2)²－3a²＝2004　∴ 4a＋4＝668　∴ a＝166 [cm²]

解答・その12

（ペンネ－ム：スモークマン）

大円の半径：R
小円の半径：r
30度の1辺がRの二等辺三角形を2個くっつけたら...正三角形が中にでき...
高さはR/2
青の面積は...12(R²-r²)/4=2004
R²-r²=2004/3=668
(r+2)²-r²=4r+4=668
4r=664
r=166

解答・その13

（ペンネ－ム：迷子の雄猫）

小さい方の円の半径を2xとおく。
正１２角形を１２等分すると頂角30度、斜辺(2X+2)cmの二等辺三角形ができる。
底辺(2X+2)cmと考えると高さは(X+1)cmの三角形ができる。
面積は(2X+2)*(X+1)/2=(X+1)*(X+1)=X²+2x+1(cm²)

また、青色の部分を除くと、底辺(2X)cm高さは(X)cmの三角形ができる。面積は
x²(cm²)
2004/12=167なので、この三角形の面積の差が167(cm²)
2x+1=167より2x=166

よって小さい方の円の半径は166cm

解答・その14

（ペンネ－ム：杖のおじさん）

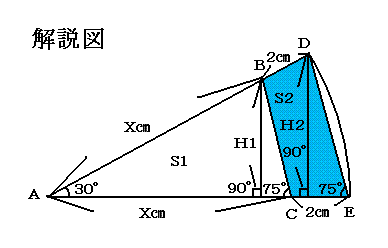
１２角形の１２分の１を切り取るとその三角形のＢＤＣＥの面積は２００４／１２＝１６７cm²になります。
切り取った三角形は小さい△ABC　と　大きい△ADE は二等辺三角形です。
（△ADE（面積）－△ABC（面積））×１２＝２００４ｃｍ²なのでこれを数式で解きます。
小さい三角形 △ＡＢＣの高さをＨ１として面積をＳ１とすると次の式になります。
S1=底辺AC（X）×H1／２
Ｈ１はＳＩＮ３０°＝Ｈ１／Ｘ　→　Ｈ１＝Ｘ／２
面積はＳ１＝Ｘ×４／Ｘ
大きい三角形 △ＡＤＥの高さをＨ2 として面積をＳ２とすると次の式になります。
S2=底辺AE（X+２）×H2／２
Ｈ２はＳＩＮ３０°＝Ｈ２／（Ｘ＋２）
2×Ｈ２＝（Ｘ＋２）→　Ｈ２＝Ｘ／２＋１
面積Ｓ２＝（Ｘ＋２）×（Ｘ／４＋１／２）
大きい三角形の面積から小さい三角形の面積を引くと次の式になります。
S2－S１=２００４／１２＝１６７ｃｍ²
（（Ｘ＋２）×（Ｘ／４＋１／２）―Ｘ×４／Ｘ）＝１６７
Ｘ＝１６７－１＝１６６ｃｍ²
答え　１６６ｃｍ²　です。

解答・その15

（ペンネ－ム：巷の夢）

題意より外円と内円の1/12部分のみを取り出し、間の部分の面積を計算してみる。
取り出した三角形はどちらも頂角30°（360°/12）の二等辺三角形であり、内円の半径をＲとすると、30°の直角三角形の高さは斜辺の1/2であるから、全体の1/12の内円と外円の間の面積をＳ、内円と外円部の三角形の面積を各々Ｓ_Ｒ、Ｓ_Ｒ＋２とすると、
　　　Ｓ＝2004/12＝Ｓ_Ｒ＋２　－Ｓ_Ｒ　＝〔（Ｒ+2）²－Ｒ²〕/4　＝Ｒ+1
因って、Ｒ＝166㎝となる。即ち、求める内円の半径は166㎝である。　

解答・その16

（ペンネ－ム：転位反応）

正十二角形を構成する十二の二等辺三角形のうちのひとつを△ABCとして図示する。　∠ACB=30°
ここで、AからBCに対して垂線を下ろし、その交点をD、AC=BC=ａとする

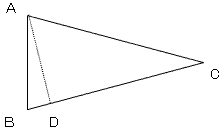
△ADCは、一辺の長さがａの正三角形の半分なので、AD＝ａ／２
よって、△ABCの面積はａ^２／４
同様にして、辺の長さがａ+２の二等辺三角形の面積は
（ａ＋２）^２／４
よって、題意より
（ａ＋２）^２／４－ａ^２／４＝２００４／１２
ａ＝１６６
小さい方の円の半径は、１６６ｃｍである。

解答・その17

（ペンネ－ム：falcon@中学教師）

＜答え＞
１６６（cm）

＜考え方＞
基本的な考え方は同じですが、３種類の方法で求めてみました。
その１は中学生の内容で充分、その２は高校生の内容まで及ぶかと。
しかし、問題の出典が、「算数」オリンピック・・・
時間があればもう少し考えてみます。

その１
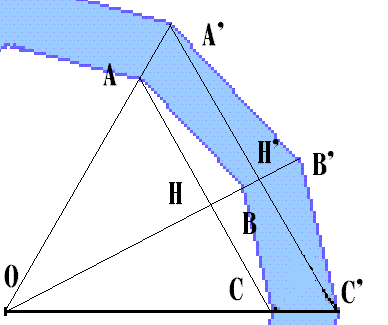まず図のように補助線を引きます。
この時点でわかることは・・・
　・OA=OB=OC=AC
　・OA'=OB'=OC'=A'C'
　・∠AOB=∠BOC=３６０°÷１２＝３０°

線分OB、OB'はそれぞれ∠AOC、∠A'OC'の二等分線になるので H、H'はそれぞれAC、A'C'の中点になる。さらにAH⊥OB、A'H'⊥OB'となる。
台形ABB'A'の面積はちょうどブルーの部分の面積の１２分の１であるので
　　　２００４÷１２＝１６７（cm²）
では、小さい方の円の半径をx ｃmとすると・・・ △OA'B'－△OAB＝台形ABB'A'であるから
　　　(x+2)/2 × (x+2) ×1/2 － x/2 × x ×1/2 ＝ 167
これを解くと、x＝１６６

その２
△OA'B'－△OAB＝台形ABB'A'を使うのは同じです。三角比を使って求めます。
　　　1/2 (x+2)² sin30°－ 1/2 x² sin30°＝　167
これを解くと、x＝１６６

その３
小さい方の円の半径を x (cm) とし、小さい方の正十二角形の面積を y (cm²) とする。
２つの正十二角形は相似な関係にあるので、以下の比を使った式が成り立つ。
　　　x² ： (x+2)² ＝ y ： y+2004
この式より内項の積、外項の積を利用して以下の式が成り立つ。
　　　(x+2)² × y ＝ x² × (y+2004)
展開して整理すると
　　　xy + y - 501x² ＝ 0 ・・・(1)
一方で、小さい方の正十二角形の面積 y を x を用いて表すと
　　　y ＝ 3x² ・・・(2)　（←これは前の解答で用いたやり方を利用して出します。）
(2)を(1)に代入して整理して解いていくと・・・
　　　3x³ - 498 x² ＝ 0
　　　x³ - 166 x² ＝ 0
　　　x² × (x-166) ＝ 0
　　　x ＝ 0 ，166
x ＝ 0 は不適なので、x ＝ 166

解答・その18

（ペンネ－ム：teki）

答え　　１６６ｃｍ

＜解法＞

１
まず、半径ｒの円に内接する正十二角形の面積は、３ｒ^２であることを証明しておきます。
半径ｒの円に内接する正十二角形を１２等分すると、頂角３０度の二等辺三角形ができます。
この面積は、３０度を挟む辺（長さ＝ｒ）を底辺とすると、高さは、1/2ｒです。
（正三角形の1/2、つまり３０度、６０度、９０度の直角三角形を考えれば明らかです。）
よって、この二等辺三角形１個の面積は、ｒ×1/2ｒ÷２＝1/4×ｒ^２です。
正十二角形の面積は、これの１２倍ですから、１２×1/4×ｒ^２＝３ｒ^２となります。

２
問題の小さい方の正十二角形に外接する円の半径をｒとすると、大きい方の正十二角形に外接する円の半径はｒ＋２です。
よって、２００４＝３×（ｒ＋２）^２－３ｒ^２＝１２ｒ＋１２　が成立します。
これを解いて、ｒ＝１６６　　ですね。
この部分は、算数で解こうとすると、面積図を描けば解けますね。
（わたしゃ、面倒なので方程式ですが・・・・・。）

解答・その19

（ペンネ－ム：夜ふかしのつらいおじさん）

その１

正12角形の１辺がつくる三角形に注目します。

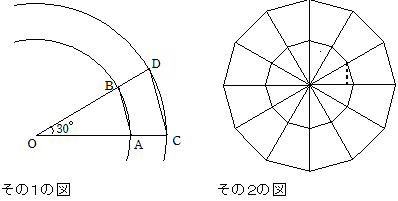
その２

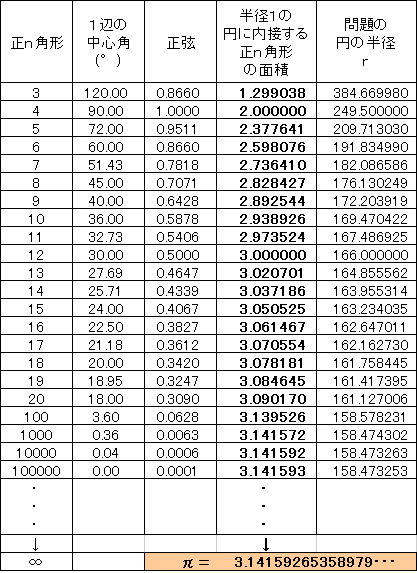
半径１の円に内接する正12角形の面積は、３です。

合同な図形の面積は、対応する長さの２乗に比例します。
だから半径ｒの円に内接する正12角形の面積は、３ｒ²、半径（ｒ＋２）の円に内接する正12角形の面積は、３（ｒ＋２）²です。
３（ｒ＋２）²ー３ｒ²＝２００４となればよいわけです。
よって、この方程式を解くと、ｒ＝１６６です。

問題の正12角形をいろいろ変えてみます。
正12角形のときは、答えが整数になるようです。

正解者

haya スモークマンのっこん

オヤジ迷子の雄猫 falcon@中学教師

長崎島原　かがみ SOU teki

転位反応巷の夢浜田明巳

namiusagi 杖のおじさんバルタン星人

夜ふかしのつらいおじさん松本峻典再出発

三角定規

まずは、図形を12等分し、三角関数を使うと大きい円の半径を求めることができますね。
三角定規にある30°、60°、90°の三角形の３辺の比が、１：２：√３であることを知っていれば、これを使って三角形の面積を求めることもできます。
夜ふかしのつらいおじさんが、おもしろいシミュレーションをしてくださいました。正12角形の2004というのは、絶妙な組み合わせのようです。

Challenge!