侾俆俁丏係寘偺惍悢
係寘偺惍悢偑偁傝傑偡丅偙偺惍悢偺奺埵偺悢帤偼偡傋偰堎側偭偰偄偰丄傑偨侽偱偼偁傝傑偣傫丅
偙偺惍悢偺悢帤傪側傜傋偐偊偰偱偒傞偡傋偰偺惍悢偺偆偪嵟戝偺惍悢偲偙偺惍悢偲偺嵎偼3618偱丄
嵟彫偺惍悢偲偙偺惍悢偲偺嵎偼4554偱偡丅偙偺係寘偺惍悢傪媮傔偰偔偩偝偄丅
栤戣偺弌揟
嶼悢僆儕儞僺僢僋偵挧愴
嶼悢僆儕儞僺僢僋埾堳夛曇
島択幮僽儖乕僶僢僋僗
2004擭僩儔僀傾儖栤戣
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗昹揷丂柧枻乯
僄僋僙儖偺儅僋儘偱夝偒傑偟偨丏摎偼俆俋侾俁偱偡丏
Option Explicit
Dim a(4) As Integer
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Range
Call saiki(1)
End Sub
Sub saiki(ByVal n As Integer)
a(n) = 1
While a(n) <= 9
If onaji(n) = 0 Then
If n < 4 Then
Call saiki(n + 1)
Else
Call check(1)
End If
End If
a(n) = a(n) + 1
Wend
End Sub
Sub check(ByVal x As Variant)
Dim b(4) As Integer
Dim s As Integer
Dim ss As Integer
Dim dame As Integer
Dim j As Integer
Dim jj As Integer
Dim jjj As Integer
For j = 1 To 4
b(j) = a(j)
Next j
For j = 1 To 4 - 1
For jj = j + 1 To 4
If b(j) < b(jj) Then
b(0) = b(j)
b(j) = b(jj)
b(jj) = b(0)
End If
Next jj
Next j
dame = 0
j = 1
While dame = 0 And j <= 2
s = 0
For jj = 1 To 4
ss = a(jj) - b(-jj * (j = 1) - (5 - jj) * (j = 2))
For jjj = 1 To 4 - jj
ss = ss * 10
Next jjj
s = s + ss
Next jj
s = Abs(s)
If (j = 1 And s = 3618) Or (j = 2 And s = 4554) Then
j = j + 1
Else
dame = 1
End If
Wend
If dame = 0 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
s = 0
For j = 1 To 4
ss = a(j)
For jj = 1 To 4 - j
ss = ss * 10
Next jj
s = s + ss
Next j
Cells(Cells(1, 1).Value, 2).Value = s
End If
End Sub
Private Function onaji(ByVal n As Integer) As Integer
Dim j As Integer
onaji = 0
j = 1
While onaji = 0 And j < n
If a(j) = a(n) Then
onaji = 1
Else
j = j + 1
End If
Wend
End Function
夝摎丒偦偺2
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
摎偊
俆俋侾俁
峫偊曽丗
暲傋懼偊偨嵟戝偺悢傪俙俛俠俢偲偡傞偲嵟彫偼俢俠俛俙
俙俛俠俢亅俢俠俛俙亖俁俇侾俉亄係俆俆係亖俉侾俈俀
俙亅俢偑俉偵側傞偺偼俙亖俋丂俢亖侾偺帪偺傒
杮棃偺悢偺枛旜乮俛傑偨偼俠乯偼丄侾侾亅俉亖俁
傑偨愭摢偼俆傑偨偼俇丄俆偺帪戣堄傪枮偨偟
尦偺悢偼俆俋侾俁
夝摎丒偦偺3
乮儁儞僱亅儉丗僆儎僕乯
夝丂丂俆俋侾俁
佹丂媮傔傞悢傪丂倶丂偲偡傞偲
丂丂丂嵟戝抣亅倶亖俁俇侾俉丂丒丒丒嘥
丂丂丂倶亅嵟彫抣亖係俆俆係丂丒丒丒嘦
嘥亄嘦傛傝
丂丂丂嵟戝抣丂亅丂嵟彫抣亖丂俉侾俈俀丂丒丒丒嘨
嘨傛傝丂俉侾俈俀亖俋俉俇侾亅侾俇俉俋丂亖丂俋俇係侾亅侾係俇俋
丂丂丂丂丂丂丂丂丂亖俋俆俁侾亅侾俁俆俋丂亖丂俋係俀侾亅侾俀係俋丂
側偳偑峫偊傜傟傞
忦審傛傝
丂丂丂丂丂俋俆俁侾丂丂丂丂丂丂侾俁俆俋 丂丂丂丂亅俁俇侾俉丂丂丂丂丂亄係俆俆係 丂丂丂丂丂俆俋侾俁丂丂丂丂丂丂俆俋侾俁
夝摎丒偦偺4
乮儁儞僱亅儉丗haya乯
5913 偱偡
亂夝偒曽亃
媮傔傞 4寘偺惍悢傪 n_ans 偲偡傞偲
丂丂丂(1) 崀弴偵寘暲傋懼偊(n_ans) - n_ans = 3618
丂丂丂(2) n_ans - 徃弴偵寘暲傋懼偊(n_ans) = 4554
(1) + (2) 偐傜
丂丂丂崀弴偵寘暲傋懼偊(n_ans) - 徃弴偵寘暲傋懼偊(n_ans) = 8172
崀弴偵寘暲傋懼偊偨係寘偺惍悢傪嵍偐傜弴偵 z, y, x, w 偲偡傞偲
z y x w - w x y z --------------------- 8 1 7 2
z - w = 8
w - z = 2 or 10 + w - z = 2
傛傝丄0 傪晄壜偲偡傟偽丄z = 9, w = 1 傪摼傞丅
(1) 傛傝
丂丂丂n_ans = 崀弴偵寘暲傋懼偊(n_ans) - 3618 = 9531 - 3618 = 5913
PS丗 昐偺埵埲壓偱 0 傪晄壜偲偟側偗傟偽 4802 傕夝偵側傝傑偡丅
夝摎丒偦偺5
乮儁儞僱亅儉丗挿嶈搰尨丂偐偑傒乯
媮傔傞惍悢傪倫丄暲傋偐偊偨嵟戝悢傪俵丄暲傋偐偊偨嵟戝悢傪倣偲偡傞丅
戣堄傛傝丄俵亅倫亖俁俇侾俉丄倫亅倣亖係俆俆係丂偩偐傜丄
偙偺俀幃傪曈乆壛偊傞偲丄
丂丂丂俵亅倣亖俉侾俈俀丂
偲側傞丅
偦偙偱丄
丂丂丂俵亖俋仩仩仩
丂丂丂倣亖侾仩仩仩
偟偐峫偊傜傟側偄偺偱丄師偵仩仩仩傪帋峴嶖岆偟偰擖傟偰傒傞偙偲偵偟偨丅
偦偟偰丄
丂丂丂俵亖俋俆俁侾
丂丂丂倣亖侾俁俆俋
偲偟偰傒傞偲丄
俵亅倣亖俉侾俈俀
偲側傞丅
師偵丄倫亖俆俋侾俁丂偲偡傞偲丄
丂丂丂俵亅倫亖俋俆俁侾亅俆俋侾俁亖俁俇侾俉
丂丂丂倫亅倣亖俆俋侾俁亅侾俁俆俋亖係俆俆係
偲側傞丅偟偨偑偭偰丄媮傔傞惍悢偼丂俆俋侾俁丂偱偁傞丅
夝摎丒偦偺6
乮儁儞僱亅儉丗柪巕偺梇擫乯
嵟戝偺惍悢傪x丄嵟彫偺惍悢傪z丄偙偺係寘偺惍悢傪y偲偍偔丅
偙偺惍悢偺奺埵偺悢帤偼偡傋偰堎側偭偰偄傞偺偱
偦傟偧傟偺悢帤傪彫偝偄弴偐傜a,b,c,d偲偍偔丅
a,b,c,d偄偢傟傕侽偱偼側偔丄
偙偺惍悢偺悢帤傪側傜傋偐偊偰偱偒傞丂偡傋偰偺惍悢偺偆偪
嵟戝偺惍悢偲偙偺惍悢偲偺嵎偼3618偱丄
嵟彫偺惍悢偲偙偺惍悢偲偺嵎偼4554偱偁傞偺偱丄
丂丂丂x-y=3618
丂丂丂y-z=4554
丂丂丂x-z=8172丂傛傝
丂丂丂1000d+100c+10b+a - (1000a+100b+10c+d) = 8172丂...乮幃1乯
d=8偲偡傞偲丄a=1偱傕x偲z偺嵎偑8000傪壓夞傞偺偱丄d=9丄a=1
幃1偵戙擖偟偰
丂丂丂9000+100c+10b+1 - (1000+100b+10c+9) = 8172
丂丂丂100c+10b - (100b+10c) = 180
丂丂丂9c-9b = 18
丂丂丂c-b = 2
傛偭偰丄(c,b) = (7,5) , (6,4) , (5,3) , (4,2)
x偺侾偺埵偑侾偱丄x-y=3618側偺偩偐傜丄
y偺侾偺埵傪峫偊傞偲丄3偱側偔偰偼側傜側偄丅
傛偭偰丄(c,b)=(5,3)偱偁傝丄偙偺惍悢偼5913
丂丂丂9531-5913=3618
丂丂丂5913-1359=4554
偱偁傞偺偱戣堄傪枮偨偡丅
夝摎丒偦偺7
乮儁儞僱亅儉丗SOU乯
崱丄奺埵偺悢帤偑 a,b,c,d 偱峔惉偝傟偰偄偰丄
丂d亜c亜b亜a
偲偄偆娭學偑偁傞偲偡傞丅
偙傟偵傛傝昞偝傟傞嵟戝偺惍悢丄嵟彫偺惍悢偼奺乆
丂1000d + 100c + 10b + a
丂1000a + 100b + 10c + d
偲側傝丄偦偺嵎偼 8172 側偺偱
丂999(d-a) + 90(c-b) = 8172丂仛
偲偄偆娭學幃偑偱偒傞丅
8172偺丄1偺埵傪寛傔傜傟傞偺偼丄嵍曈偺 999(d-a) 偺晹暘偩偗偱丄
丂d-a = 8
偱側偗傟偽側傜側偄丅
忦審偐傜丄
丂(d,a)=(9,1)
埲奜偵柍偄偙偲偑傢偐傞丅偡傞偲仛偼
丂c-b = 2
偲側傞丅慻傒崌傢偣偲偟偰偼丄
丂(c,b) = (4,2),(5,3),(6,4),(7,5),(8,6)
偑偁偘傜傟傞偑丄偙偺拞偱巆傝擇偮偺忦審傪枮偨偡傕偺偼
丂(c,b) = (5,3)
偺慻偺傒丅埲忋偺帠偐傜尦偺惍悢偼 5913 //
夝摎丒偦偺8
乮儁儞僱亅儉丗偺偭偙傫乯
嵟彫偺惍悢偺愮偺埵傪a,昐偺埵傪b,廫偺埵傪c,堦偺埵傪d 偲偡傞
丂乮埲壓偙傟傪 abcd 偺傛偆偵昞傢偡乯
嵟戝偺惍悢偼 dcba 偲昞傢偝傟傞
3618 + 4554 = 8172 偩偐傜 abcd+8172=dcba 丒丒丒(1) 偲側傞
(1) 偺昐偺埵偺寁嶼偵偍偄偰丂b亝俈 偩偐傜丂b+1亝8, b+2亝9
傛偭偰昐偺埵偐傜愮偺埵傊偺孞傝忋偑傝偼側偄
a+8=d 傛傝 a=1,d=9
(1) 偵a=1,d=9 傪戙擖偟偰丂1bc9+8172=9cb1丒丒丒(2) 偲側傞
(2) 偺堦偺埵偺寁嶼偵偍偄偰丂9+2=11 偩偐傜丂廫偺埵偺寁嶼偼 c+8 偲側傞
c亞3 偩偐傜 c+8亞11 傛偭偰昐偺埵偺寁嶼偼 b+2 偲側傞
b+2=c 傪枮偨偡偺偼師偺俆偮
(b,c)=(2,4),(3,5),(4,6),(5,7),(6,8)
(a,b,c,d)=(1,2,4,9) 偺帪丄媮傔傞惍悢偼5803丒丒丒偙傟偼1,2,4,9 偺暲傋懼偊偱偼側偄
丂丂丂丂丂=(1,3,5,9) 偺帪丄丂丂丂乂丂丂丂5913丒丒丒偙傟偼1,3,5,9 偺暲傋懼偊偱偁傞
丂丂丂丂丂=(1,4,6,9) 偺帪丄丂丂丂乂丂丂丂6023丒丒丒偙傟偼1,4,6,9 偺暲傋懼偊偱偼側偄
丂丂丂丂丂=(1,5,7,9) 偺帪丄丂丂丂乂丂丂丂6133丒丒丒偙傟偼1,5,7,9 偺丂丂丂丂乂
丂丂丂丂丂=(1,6,8,9) 偺帪丄丂丂丂乂丂丂丂6243丒丒丒偙傟偼1,6,8,9 偺丂丂丂丂乂
傛偭偰媮傔傞惍悢偼丂5913
傕偭偲娙扨側夝偒曽偑偁傞傫偩傠偆側偁乣
偄偄栤戣偩偲巚偄傑偡
夝摎丒偦偺9
乮儁儞僱亅儉丗falcon@拞妛嫵巘乯
亙摎偊亜
5913
亙峫偊曽亜
媮傔傞惍悢傪 X 偲偟丄係寘傪峔惉偟偰偄傞係偮偺悢帤傪 a, b, c, d 偲偡傞丅
偝傜偵堦堄惈偼曄傢傜側偄偺偱丄a亜b亜c亜d 偲偡傞丅
昞尰傪娙扨偵偟偨偄偺偱丄
側傜傋偐偊偰偱偒傞嵟戝偺惍悢傪 abcd
嵟彫偺惍悢傪 dcba 偲昞尰偡傞偙偲偵偡傞丅
梌偊傜傟偨忦審偼
丂丂丂abcd亅X亖3618
丂丂丂X亅dcba亖4554
偙偺俀偮偺幃傪懌偟偰丄abcd亅dcba亖8172偲偄偆幃傪嶌傞丅
偙偙偱係寘栚偺寢壥偵拲栚偡傞偲丄
奺寘偼侾乣俋偺悢偺傒傪梡偄傞偙偲偑忦審側偺偱丄a=9, d=1 偲寛傑傞丅
師偵丄巆傝偺b, c 傪寛掕偡傞偨傔偵昅嶼偺宍傪庢偭偰峫偊偰傒傞丅
丂俋倐們侾 亅侾們倐俋 亅亅亅亅亅 俉侾俈俀係寘栚偼孞傝壓偑傝偺塭嬁傪庴偗偢丄侾寘栚偱孞傝壓偑傝偑婲偙傞偺偼柧敀丅
偁偲偼俀寘栚偱孞傝壓偑傝偑婲偙傞偐偳偆偐丅
乮侾乯孞傝壓偑傝偑婲偙傜側偄偲偡傞偲丒丒丒
俀寘栚偺寁嶼偼乮們亅侾乯亅倐亖俈
俁寘栚偺寁嶼偼倐亅們亖侾
偙偺俀偮偺幃偺楢棫曽掱幃偵偼夝偑側偄偺偱晄揔
乮俀乯孞傝壓偑傝偑婲偙偭偨偲偡傞偲乧
俀寘栚偺寁嶼偼侾侽亄乮們亅侾乯亅倐亖俈
俁寘栚偺寁嶼偼乮倐亅侾乯亅們亖侾
偙偺俀偮偺幃偺楢棫曽掱幃偵偼夝偑柍悢偵懚嵼偟丄偦偺忦審偼倐亅們亖俀
傛偭偰丄孞傝壓偑傝偑婲偙偭偨偲偟偰巆偭偰偄傞悢帤偐傜峫偊傞偲
乮倐丆們乯亖乮俉丆俇乯丄乮俈丆俆乯丄乮俇丆係乯丄乮俆丆俁乯丄乮係丆俀乯
尦乆梌偊傜傟偰偄傞忦審偺堦偮丄abcd亅X亖3618
偙傟傪曄宍偝偣偰X亖abcd亅3618偲偟偰偙偺幃偵岓曗傪摉偰偼傔偰偄偔偲
戣堄偵崌偆偺偼乮倐丆們乯亖乮俆丆俁乯偺傒偱丄X亖5913偲弌偰偔傞丅
乮傕偆堦偮偺忦審幃偵摉偰偼傔偰妋擣偡傞偲丄傗偼傝偙傟傕惉傝棫偮丅乯
夝摎丒偦偺10
乮儁儞僱亅儉丗K偺恖乯
4寘偺悢偺奺寘偺悢傪 a,b,c,d 偲偟丄 d亙c亙b亙a 偲偡傞丅
4寘偺悢傪暲傃懼偊偰偱偒傞嵟戝偺悢偲偙偺悢偲偺嵎偑3618丄
嵟彫偺悢偲偺嵎偑4554偱偁傞偺偱嵟戝偺悢偲嵟彫偺悢偲偺嵎偼 3618+4554=8172 偲側傞丅
偙偺偙偲偐傜丄
丂丂丂(1000a+100b+10c+d)-(1000d+100c+10b+a)=8172
偲偄偆幃偑惉傝棫偮丅偙傟傪惍棟偟偰丄
丂丂丂111(a-d)+10(b-c)=908
偝偰 a,b,c,d 偼偦傟偧傟1寘偺0偱側偄帺慠悢偱 d亙c亙b亙a 偱偁傞偺偱 a-d , b-c 傕偦傟偧傟1寘偺0偱側偄帺慠悢偱偁傞丅
偙偺偙偲偐傜丄 111(a-d) 偼 333,444,555,666,777,888
(1亝a亝6,4亝d亝9偱偁傞偺偱)偺偄偢傟偐偱偁傝丄10(b-c) 偼
10,20,30,40,50,60(2亝c亝7,3亝b亝8偱偁傞偺偱)偺偄偢傟偐偱偁傞丅
111(a-d)+10(b-c)=908 偱偁傝丄908 偺1偺埵偑8偱丄10(b-c) 10,20,30,40,50,60偺偄偢傟偐側偺偱
丂丂丂111(a-d)=888
丂丂丂a-d=8
丂丂丂10(b-c)=20
丂丂丂b-c=2
偱偁傞丅
a-d=8偲側傞慻傒崌傢偣偼丄a=9,d=1偺傒偱偁傞丅
b-c=2偲側傞慻傒崌傢偣偼a=9,d=1偱偁傞偙偲傪峫偊偰丄
丂丂丂(b=8,c=6),(b=7,c=5),(b=6,c=4),(b=5,c=3),(b=4,c=2)
偱偁傞丅
a=9,d=1偲偟丄b,c偲忋婰偺慻傒崌傢偣偺拞偐傜慖傫偱偦傟偧傟傪暲傃懼偊偨嵟戝偺悢傪嶌傞偲偦傟偧傟
9861,9751,9641,9531,9421 偱偁傞丅偙傟傜悢偐傜偦傟偧傟3618傪堷偔偲弴偵
6243,6133,6123,5913,5803 偲側傞丅
偙傟傜偺悢偺拞偱3618傪堷偄偨偁偲偺悢偺奺寘偺悢傪暲傃懼偊偰堷偔慜偺悢偵側傞偺偼5913偺傒偱偁傞丅
5913偺奺寘偺悢傪暲傃懼偊偰偱偒傞嵟彫偺悢偼1359丅偙傟偲尦偺悢偲偺嵎偼4554偱偁傝摎偊偲偟偰傆偝傢偟偄丅
傛偭偰媮傔傞傋偒悢偼丄5913
夝摎丒偦偺11
乮儁儞僱亅儉丗揮埵斀墳乯
係寘偺惍悢傪俼丄嵟戝媦傃嵟彫偺惍悢傪偦傟偧傟俼max丄俼min偲偡傞丅
丂丂丂俼min亙俼亙俼max丂側偺偱
丂丂丂俼max亅俼min亖俁俇侾俉亄係俆俆係亖俉侾俈俀
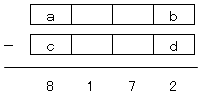
倎丆們偵偮偄偰偼丄倎亖俋丆們亖侾偺応崌偵尷傜傟傞偺偱
戣堄偐傜丄倐亖侾丆倓亖俋
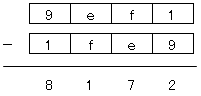
廬偭偰丄嵎偑侾俉偲側傞俀寘偺惍悢傪尒偮偗傟偽椙偄丅
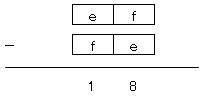
峫偊傜傟傞慡偰偺俀寘偺惍悢偺慻崌偣偼埲壓偺捠傝丅
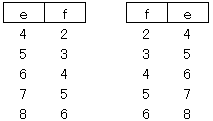
偦傟偧傟偺慻崌偣偵偮偄偰専徹偡傞偲丄
媮傔傞係寘偺惍悢偼丄俼亖俆俋侾俁

夝摎丒偦偺12
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
偙偺惍悢偵巊傢傟偰偄傞係屄偺悢帤傪彫偝偄弴偵a,b,c,d偲偟傑偡丅
傑偨偙偺悢傪pqrs偱昞偟傑偡丅乮p,q,r,s偼丄偦傟偧傟a,b,c,d偺偳傟偐乯
偡傞偲丄


媮傔傞夝摎偼俆俋侾俁偱偡丅
夝摎丒偦偺13
乮儁儞僱亅儉丗岼偺柌乯
戣堄傛傝媮傔傞4寘偺惍悢傪Y丄嵟戝悢傪X丄嵟彫悢傪Z偲偡傞偲
丂丂丂X-Y亖3618丂丒丒丒丒丒丒(1)
丂丂丂Y-Z亖4554丂丒丒丒丒丒丒(2)
偙偺(1)偍傛傃(2)傛傝Y偺4寘栚偼嵟戝悢偱側偔丄嵟彫悢偱傕側偄偲傢偐傞丅
丂丂丂(1)+(2)傛傝X-Z亖8172丂丒丒丒丒丒(3)
偙傟傛傝X偺4寘栚偼9丄Z偺4寘栚偼1偱偁傞丅偡傞偲巆傝偺2悢偼乮2,3,4,5,6,7,8乯偺拞偺擇偮偱偁傞丅
X偼9仜仮1丄Z偼1仮仜9偲彂偗傞丅
偙傟傛傝丂仮-仜亖8側偄偟10-仜丂+仮-1亖7丄懄偪丄仜-仮亖2偱偁傞丅仮-仜亖8偲側傞偵偼9偲1偟偐側偔丄
偙傟傜偼婛偵妋掕偟偰偄傞偺偱丄仜-仮亖2偱偁傞丅
場偭偰丄乮仜丄仮乯亖乮8,6乯乮7,5乯乮6,4乯乮5,3乯乮4,2乯偺偳傟偐偱偁傞丅
偲偙傠偱丄(1)偲(2)傛傝Y偺4寘栚偼5偐6偱偁傞偲暘偐傞丅
偙傟傛傝丄6側傜乮仜丄仮乯亖乮8,6乯側偄偟乮6,4乯
5側傜乮仜丄仮乯亖乮7,5乯側偄偟乮5,3乯丂偲側傞丅
埲忋傛傝乮X丄Z乯偼乮9861,1689乯乮9641,1469乯乮9751,1579乯乮9531,1359乯偲側傞丅
偙偺4働乕僗偺Y傪媮傔傞偲丄奺乆7243,6023,6133.5913偲側傞丅
偙偺偆偪婛抦偺9偲1偑擖偭偰偄傞惍悢偼5913偺傒偱偁傝丄偙傟偑媮傔傞傕偺偱偁傞丅
夝摎丒偦偺14
乮儁儞僱亅儉丗teki乯
係寘偺悢偵巊傢傟偰偄傞係偮偺悢帤傪丄彫偝偄弴偵a,b,c,d偲偟傑偡丅
傕偲偺悢傪A偲偡傞偲丄
丂丂丂A-1000a-100b-10c-d亖3618
丂丂丂1000倓+100們+10倐+a-A亖4554
偑惉棫偟傑偡丅曈乆懌偟偰丄
丂丂丂1000*乮d-a)+100*(c-b)+10*(b-c)+a-d亖8172
尦偺悢傕暲傋懼偊偨悢傕係寘側偺偱丄愮偺埵偑俉偱偁傞偙偲偐傜
丂丂丂d=9 , a=1
偱偡丅傑偨丄10偺埵偼侾偺埵偺堷偒嶼偐傜
丂丂丂倐-們+9亖7丄
100偺埵偼侾0偺埵偺堷偒嶼偐傜
丂丂丂們-倐-侾亖1
偱丄倐亖俁丄們亖俆丂偲側傝傑偡丅
夝摎丒偦偺15
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂俆俋侾俁
偙偺惍悢偺奺寘偺悢傪戝偒偄弴偵A,B,C,D偲偡傞偲嵟戝偺悢帤偼A,B,C,D偱
嵟彫偺悢帤偼D,C,B,A偲側傝傑偡丅
乮椺丂媮傔傞悢帤偑俆俀俁俋偲偡傞偲俋俆俁俀偑嵟戝偱俀俁俆俋偑嵟彮偵側傝傑偡丅乯
嵟戝偐傜嵟彫傪堷偔偲俁俇侾俉亄係俆俆係亖俉侾俈俀偲側傝傑偡丅
廬偭偰係寘栚偼俋偐傜俋亅X=8丂仺X=9-8=1
偙偺係寘偵俋偲侾偑擖偭偰偄傞偙偲偑暘偐傝傑偡丅A,B,C,D,偼侽埲奜側偺偱A=9
D=1偲側傝傑偡丅
ABCD-DCBA=俋BC1-侾CB俋亖俋侽侽侾亅侾侽侽俋亄BC侽亅CB侽亖俈俋俋俀亄BC0亅CB0亖俉侾俈俀
乮BC亅CB乯亊侾侽亖俉侾俈俀亅俈俋俋俀亖侾俉侽
廬偭偰BC亅CB=18
B亜C偱偁傝B偲C偼俋偲侾埲奜偺悢側偺偱偔傝壓偑偭偰俉偲側傞偨傔偵偼B亅C=侾亄侾亖俀偵側傜側偗傟偽側傜側偄丅
偦偺忦審偵摉偨傞偺偑師偺俆捠傝偲側傝傑偡丅
乮係丆俀乯乮俆丆俁乯乮俇丆係乯乮俈丆俆乯乮俉丆俇乯嵟戝偺惍悢偼
俋BC1亅俁俇侾俉亖仩仩仩俁偲側傝傑偡丅
B偲C偺偳偪傜偐偑俁偱偁傞偙偲偑暘偐傝傑偡丅
偙傟偵傛傝忋婰偺慻傒崌傢偣偺拞偐傜B=3丂C=5偱偁傞偙偲偑暘偐傝傑偡丅
俋俆俁侾亅俁俇侾俉亖俆俋侾俁偲側傝傑偡丅
嵟戝偺悢帤偐傜媮傔傞悢帤傪堷偔偲俁俇侾俉側偺偱
俋俆俁侾亅X=俁俇侾俉仺俋俆俁侾亅俁俇侾俉亖俆俋侾俁
摎偊丂俆俋侾俁偱偡丅
夝摎丒偦偺16
乮儁儞僱亅儉丗lotus乯
奺寘偺悢巐偮傪愮偺埵偐傜戝偒偄弴偵暲傋懼偊偨嵟戝悢偲彫偝偄弴偵暲傋懼偊偨嵟
彫悢偺嵎偼丄3618+4554=8172丂偲側傞丅
偳偺寘偺悢傕0偱偼側偔1偐傜9傑偱偺惍悢偱偁傞偐傜丄嵎偑8000戜偵側傞偺偼
愮偺埵偺悢偑9偲1偺応崌偟偐偁傝摼側偄丅
廬偭偰丄嵟戝悢偼丂9仜仮侾丆嵟彫悢偼1仮仜9丂乮仜亜仮乯偲側傝丄戣堄傪枮偨偡仜偲仮偺悢
帤傪媮傔偰偄偔丅
9仜仮侾-8172=1仮仜9丂壓嶰寘偵拝栚偟
仜仮侾-172=仮仜9丂仺丂10+(仮-1)-7=仜(廫偺埵乯丄仜-1-仮=1(昐偺埵)丂偮傑傝仜-仮=2
偟偨偑偭偰(仜丄仮)偼(8,6)(7,5)(6,4)(5,3)(4,2)偺偄偢傟偐偱偁傞丅
(1偲9偼婛偵巊偭偰偄傞偺偱(9,7)偲(3,1)偼晄壜乯
尦偺悢偐傜1仮仜9傪堷偄偨嵎偑4554側偺偱丄尦偺悢偺堦偺埵偺悢偼3偲暘偐傝丄
(仜丄仮)偺慻傒崌傢偣偱3偑娷傑傟偰偄傞傕偺偼(5,3)偟偐側偄丅
埲忋偐傜4偮偺悢1,3,5,9偑敾柧偟偨偺偱丄偁偲偼忦審傪枮偨偡悢傪媮傔傟偽椙偔丄
摎偊偼丂5913丂偱偁傞丅
夝摎丒偦偺17
乮儁儞僱亅儉丗嶰妏掕婯乯
媮傔傞4寘偺惍悢傪 N丆N 傪暲傋懼偊偰偱偒傞嵟戝悢傪 Max丆嵟彫悢傪 min 偲偡傞偲丆戣堄傛傝
丂丂Max亅N亖3618 乧 (1)
丂丂N亅min亖4554 乧 (2)
(1)亄(2)丗 Max亅min亖8172 乧 (3)
(3)傛傝丆N 偺奺埵偺悢偼 1丆9 傪娷傒丆Max亖9仩仮1丆min亖1仮仩9 乧 (4)
(4)傪(3)偵戙擖偟偰丆仩仮亖86丆75丆64丆53丆42 乧 (5)
(1)亅(2)丗 Max亄min亅2N亖亅936丂亪 N亖(Max亄min亄936)/2 乧 (6)
(5)偺奺悢傪(6)偵戙擖偟戣堄傪枮偨偡傕偺偼 仩仮亖53 偱丆N亖5913 乧[摎]
惓夝幰
| falcon@拞妛嫵巘 | teki | 僶儖僞儞惎恖 |
| 僆儎僕 | 柪巕偺梇擫 | 偺偭偙傫 |
| haya | 岼偺柌 | lotus |
| 挿嶈搰尨丂偐偑傒 | 揮埵斀墳 | K偺恖 |
| 昹揷柧枻 | 忨偺偍偠偝傫 | 嶰妏掕婯 |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | SOU |
僐儊儞僩
3618偲4554傪懌偡偲丄嵟戝偺惍悢偲嵟彫偺惍悢偺嵎偵側偭偰偄傞偲偄偆
偲偙傠偑億僀儞僩偱偟傚偆偐丅偦偙傪庤妡偐傝偵丄係偮偺悢帤傪峣傝偙傫偱偄偒傑偡偑丄
嶰妏掕婯偝傫偺夝摎偵偁傞傛偆偵丄崱搙偼3618偲4554偺嵎傪
峫偊傞偲偄偆偺傕丄偍傕偟傠偄敪憐偩側偁偲巚偄傑偡丅
 top
top