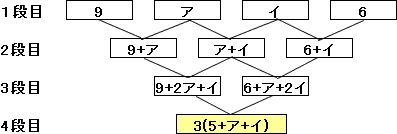
侾俆俀丏侾寘偺懌偟嶼
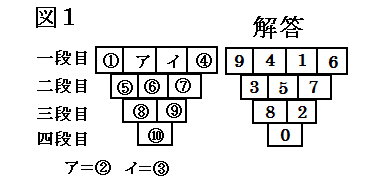
恾侾偺侾抜栚偺仩偺拞偵侾寘偺惍悢傪擖傟丄偲側傝崌偭偨悢偺寘傪寁嶼偟丄
偦偺堦偺埵偺悢傪俀抜栚偺仩偺拞偵擖傟傑偡丅摨偠傛偆偵丄俀抜栚偺偲側傝崌偭偨悢偺榓傪寁嶼偟丄
偦偺堦偺埵偺悢傪俁抜栚偺仩偺拞偵擖傟傑偡丅偝傜偵丄俁抜栚偺偲側傝崌偭偨悢偺榓傪寁嶼偟丄
偦偺堦偺埵偺悢傪係抜栚偺仩偺拞偵擖傟傑偡丅
恾俀偼丄侾抜栚偵乮俁丆侽丆俆丆俋乯傪擖傟偨偲偒偺椺偱偡丅
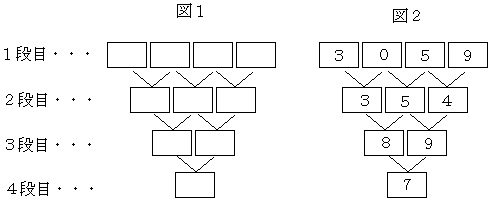
偄傑丄侾抜栚偐傜係抜栚傑偱偺10屄偺仩偺拞偵丄侽偐傜俋偺10屄偺悢帤偑
侾偮偢偮擖傞傛偆偵偟偨偄偲巚偄傑偡丅偨偩偟丄俇偲俋偺
埵抲偼恾俁偺傛偆偵寛傑偭偰偄傑偡丅
偙偺偲偒丄師偺奺栤偄偵摎偊偰偔偩偝偄丅
(1)係抜栚偺仩偵擖傞悢偼壗偱偡偐丅
(2)傾丄僀偵擖傞悢傪媮傔側偝偄丅
栤戣偺弌揟
僙儞僗偺傛偄擼傪偮偔傞丂戝恖偺嶼悢僷僘儖
壨悾丂岤丂挊
帺桼崙柉幮
愱廋戝妛徏屗拞妛峑丂2006擭
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗傗側偣乯
栤偄侾偺摎偊偼丂丂丂侽丂偱偡
栤偄俀偺摎偊丂丂丂傾偵偼丂係丂偱丂丂丂僀偵偼丂侾丂偱偡丅
偱傕側偤偦偆側傞偺偐丄懠偺悢帤偱偼側偤僟儊側偺偐偺悢妛揑徹柧偼
憡曄傢傜偢夝傜側偄丒丒丒丒丒
偟傜傒偮傇偟偺僄僋僙儖棅傝乮儅僋儘偼巊偊側偄丒丒抦傜側偄乯
嵟屻偑侽偭偰偺偼丄摨偠悢帤傪俀搙偲巊梡偟側偄偭偰強偐傜
悇應偑偮偒傑偟偨偗偳偹乮偁偔傑偱傕悇應偱偡丒丒丒姶丠乯
偦偙偐傜丄俇偲俋偑婛偵巊傢傟偰偄傞偺偱
俁抜栚偼俁偲俈偐丂丂俉偲俀堄奜偵柍偄偲峫偊偰
傑偭偦傫側強偐傜丄怓乆扵偭偰偺摎偊偱偡丅
夝摎丒偦偺2
乮儁儞僱亅儉丗僆儎僕乯
夝摎丂乮侾乯丂侽丂丂乮俀乯傾丗係丂丂僀丗侾
佹丂乮侾乯搑拞偺抜偱丄侽偑尰傟傞偲忋壓偺抜偱摨偠悢帤偑尰傟傞偨傔丅
丂丂乮俀乯俁恾偺俁抜栚偼丄乽俀偲俉乿傑偨偼丄乽俁偲俈乿偺俀庬椶偟偐懚嵼偟側偄丅丂
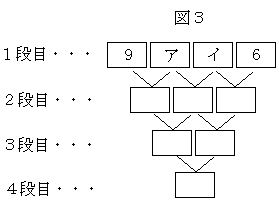
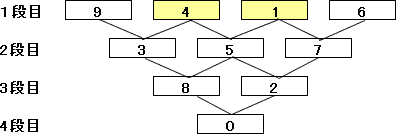
9 4 1 6
3 5 7
8 2
0
夝摎丒偦偺3
乮儁儞僱亅儉丗teki乯
侾丂侽
俀丂傾丂係丂丂僀丂侾
係抜栚偼侽偟偐偁傝摼傑偣傫丅
側偤偐偭偰丠丂俁抜栚傛傝忋抜偵侽偑偁傞偲丄摨堦悢帤偑昁偢尰傟傞偐傜偱偡丅
偱丄俁抜栚偼乮俀丏俉乯枖偼乮俁丏俈乯偺慻傒崌傢偣偲側傝傑偡丅
屻偼帋峴嶖岆偱丒丒丒丒丒丒丅
俋丂係丂侾丂俇 丂俁丂俆丂俈 丂丂俉丂俀 丂丂丂侽
夝摎丒偦偺4
乮儁儞僱亅儉丗嶰妏掕婯乯
(1) 係抜栚偵擖傞悢帤偼丆0 乧[摎]
側偤側傜丆懠偺応強偵 0 偑擖傞偲偡傞偲丆椬偺悢偲偺榓偑椬偺悢偲側傝丆
乽悢偑 1 偮偢偮擖傞乿 偲偄偆忦審偵斀偡傞偐傜丅
(2) 恾俁偺偲偒丆嬻棑偵擖傞偡傋偰偺悢偼壓偺恾偺傛偆偵側傝傑偡丅戝曄忕挿偵側傞偺偱愢柧偼徣棯偟傑偡丅
傛偭偰丆傾 偼 4丆僀 偼 1 乧[摎]
夝摎丒偦偺5
乮儁儞僱亅儉丗haya乯
(1) 0
(2) 4, 1
亂夝偒曽亃
(1) 堦斣壓偺敔埲奜偱 侽 傪巊偆偲椬偺悢帤偲摨偠悢抣偑壓偵弌偰廳暋偟偰偟傑偆偺偱丄
堦斣壓偺敔偼昁慠揑偵 侽 偲側傞丅
(2) 偦偆偡傞偲丄堦偮忋偺敔偼丄3 偲 7 偐 2 偲 8 偲側傞丅丂
巆偭偨悢帤偺慻崌偣傪帋偡偲丄3 偲 7 偱偼晄惉棫丄8 偲 2 偱壓恾偺傛偆側慻崌偣偺傒偑戣堄傪枮懌偡傞丅丂
廬偭偰夝偼丄4, 1 偱偡丅
丂俋 係 侾 俇 丂丂V V V 丂丂俁 俆 俈 丂丂丂V丂V 丂丂 俉 俀 丂丂丂 V 丂丂丂 侽
夝摎丒偦偺6
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
侾乯侽
俀乯傾係丂僀侾
峫偊曽丗
侾乯侽偑懠偺埵抲偵棃傞偲丄摨偠悢偑弌棃傞偺偱晄揔丅
俀乯俁抜栚偺榓偼侾侽丅俇丆俋偑巊傢傟偰偄傞偺偱乮俀丆俉乯傑偨偼乮俁丆俈乯丅
乮俀丆俉乯側傜偽俀抜栚偵係偼擖傟側偄乮係亄俉亖侾俀丆係亄係亖俉乯
偐傜丄傾偑係丅偦偺嵍壓偼俁丅俋偑巊傢傟偰偄傞偺偱偦偺壓偼俉丅
埲壓丄堭偯傞偱
丂丂俋丂係丂侾丂俇 丂丂丂俁丂俆丂俈 丂丂丂丂俉丂俀 丂丂丂丂丂侽俁抜栚偑乮俁丆俈乯側傜侾抜栚偵係偼擖傟側偄偺偱俀抜栚偵側傞偑 俀抜栚偱傕係亄俋亖侾俁丆係亄俁亖俈偲俁抜栚偺俁傑偨偼俈傪 嶌傞偙偲偑弌棃側偄偨傔柕弬丅 屘偵丄忋婰偑桞堦夝丅
夝摎丒偦偺7
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
0乣9 傑偱偺榓=45 側偺偱...嵟屻偺壓堦寘偼5偺傛偆側婥偑偟偨偗偳...
0偑搑拞偵偁偭偨傜摨偠悢偑偱傞偐傜...嵟屻偼0
偦偺忋偼丄2-8,3-7 偟偐側偄丅
丂7=2+5
偟偐偟丄2=6+6=3+9 側偺偱柍棟丅
丂8=1+7=3+5
偟偐偟丄1=2+9=6+5
側偺偱丄柍棟丅
偮傑傝丄8=3+5
9 4 1 6 3 5 7 8 2 0偱價儞僑侓
媡偩偲柍棟側偺偼埲壓偩偐傜...
9 8 7 6 7 5 3 2 8 0寢嬊丄
(1)係抜栚偺仩偵擖傞悢偼壗偱偡偐丅丒丒丒0
(2)傾丄僀偵擖傞悢傪媮傔側偝偄丅丒丒丒傾丗4,僀丗1
偺堦捠傝偵寛掕偝傟偨侓
夝摎丒偦偺8
乮儁儞僱亅儉丗偺偭偙傫乯
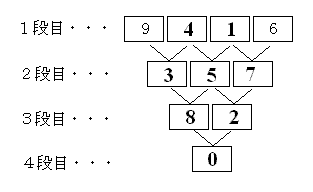
俀抜栚傪嵍偐傜僂丄僄丄僆
俁抜栚傪嵍偐傜僇丄僉
係抜栚傪 僋 偲偡傞
乮侾乯侽偼侾抜栚偵傕俀抜栚偵傕俁抜栚偵傕擖傞偙偲偑偱偒側偄偺偱丂僋亖侽
丂丂乮侾抜栚偵擖傞偲侾抜栚偲俀抜栚偱悢帤偑廳暋偡傞丄
丂丂丂俀抜栚偵擖傞偲俀抜栚偲俁抜栚偱悢帤偑廳暋偡傞丄
丂丂丂俁抜栚偵擖傞偲俁抜栚偲係抜栚偱悢帤偑廳暋偡傞乯
乮俀乯乮僇丄僉乯亖乮俀丄俉乯傑偨偼乮俉丄俀乯傑偨偼乮俁丄俈乯傑偨偼乮俈丄俁乯側偺偱偙偺係偮偺応崌偵暘偗傞
俙丏乮僇丄僉乯亖乮俀丄俉乯偺帪
丂丂乮僂丄僄乯亖乮俆丄俈乯傑偨偼乮俈丄俆乯側偺偱
丂丂乮僂丄僄丄僆乯亖乮俆丄俈丄侾乯傑偨偼乮俈丄俆丄俁乯丒丒丒丒偄偢傟傕晄揔
俛丏乮僇丄僉乯亖乮俉丄俀乯偺帪
丂丂乮僄丄僆乯亖乮俆丄俈乯傑偨偼乮俈丄俆乯側偺偱
丂丂乮僂丄僄丄僆乯亖乮俁丄俆丄俈乯傑偨偼乮侾丄俈丄俆乯
丂丂乮僂丄僄丄僆乯亖乮俁丄俆丄俈乯偼丂乮傾丄僀乯亖乮係丄侾乯偺帪丄戣堄傪枮偨偡
丂丂乮僂丄僄丄僆乯亖乮侾丄俈丄俆乯丒丒丒丒晄揔
俠丏乮僇丄僉乯亖乮俁丄俈乯偺帪
丂丂乮僄丄僆乯亖乮俀丄俆乯傑偨偼乮俆丄俀乯側偺偱
丂丂乮僂丄僄丄僆乯亖乮侾丄俀丄俆乯傑偨偼乮俉丄俆丄俀乯丒丒丒丒偄偢傟傕晄揔
俢丏乮僇丄僉乯亖乮俈丄俁乯偺帪
丂丂乮僂丄僄乯亖乮俀丄俆乯傑偨偼乮俆丄俀乯側偺偱
丂丂乮僂丄僄丄僆乯亖乮俀丄俆丄俉乯傑偨偼乮俆丄俀丄侾乯丒丒丒丒偄偢傟傕晄揔
摎偊丒丒丒乮傾丄僀乯亖乮係丄侾乯
夝摎丒偦偺9
乮儁儞僱亅儉丗falcon@拞妛嫵巘乯
亙摎偊亜
乮侾乯丂侽
乮俀乯丂傾亖係丄僀亖侾
亙峫偊曽亜
傑偢丄侾乣俁抜栚偱侽偲偺壛朄偑峴傢傟傞偲抜偺忋壓偱摨偠悢偑弌偰偒偰偟傑偆偺偱
侽偑擖傞偺偼4抜栚偵尷傜傟傞丅
偟偨偑偭偰栤戣乮侾乯偺摎偊偼丂侽
師偵3抜栚傪峫偊傞丅
4抜栚偱侽偑弌傞偨傔偵偼丄懌偟偰侾侽偵側傞2悢偺暲傃偱側偄偲偄偗側偄丅
偨偩偟丄1抜栚偱俋偲俇偑巊傢傟偰偄傞偺偱
3抜栚偺壜擻惈偼乮俀丆俉乯丄乮俉丆俀乯丄乮俁丆俈乯丄乮俁丆俈乯偺係捠傝偵側傞丅
偄偭偨傫丄偙偙偱奺仩偺拞偵擖傞悢帤偑丄偳偺傛偆側悢偺堦偺埵偱偁傞偐傪恾帵偡傞偲丒丒丒
侾抜栚丒丒丒俋丂丂丂丂丂丂丂丂傾丂丂丂丂丂丂丂丂丂丂丂僀丂丂丂丂丂丂丂丂丂丂丂俇 俀抜栚丒丒丒丂丂俋亄傾丂丂丂丂丂丂丂丂丂傾亄僀丂丂丂丂丂丂丂丂丂僀亄俇 俁抜栚丒丒丒丂丂丂丂丂俋亄俀亊傾亄僀丂丂丂丂丂傾亄俀亊僀亄俇 係抜栚丒丒丒丂丂丂丂丂丂丂丂丂丂俋亄俁亊乮傾亄僀乯亄俇丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俀乣係抜栚偼嵍恾偺幃偱昞偝傟傞悢偺堦偺埵乯係抜栚偑侽偩偲傢偐偭偰偄傞偺偱
俋亄俁亊乮傾亄僀乯亄俇亖乮侾侽偺攞悢乯偲側傝丄
偙偺娭學幃偐傜傢偐傞傾偲僀偺壜擻惈偼乮侾丆係乯丄乮係丆侾乯丄乮俀丆俁乯丄乮俁丆俀乯丄乮俈丆俉乯丄乮俉丆俈乯
偟偐偟丄3抜栚偺壜擻惈偑乮俀丆俉乯丄乮俉丆俀乯丄乮俁丆俈乯丄乮俁丆俈乯偩偭偨偙偲傪峫椂偵擖傟傞偲
傾偲僀偺壜擻惈偼乮侾丆係乯丄乮係丆侾乯偺俀捠傝偵峣傜傟傞丅
偁偲偼丄戙擖偟偰帋偟偰傒傞丅
乮傾丆僀乯亖乮侾丆係乯偩偲偡傞偲丒丒丒
侾抜栚丒丒丒俋丂丂丂侾丂丂丂係丂丂丂俇 俀抜栚丒丒丒丂丂侽丂丂丂俆丂丂丂侽 俁抜栚丒丒丒丂丂丂丂俆丂丂丂俆 係抜栚丒丒丒丂丂丂丂丂丂侽偲側傝丄晄揔
乮傾丆僀乯亖乮係丆侾乯偩偲偡傞偲丒丒丒
侾抜栚丒丒丒俋丂丂丂係丂丂丂侾丂丂丂俇 俀抜栚丒丒丒丂丂俁丂丂丂俆丂丂丂俈 俁抜栚丒丒丒丂丂丂丂俉丂丂丂俀 係抜栚丒丒丒丂丂丂丂丂丂侽偲側傝丄偆傑偔偄偔丅
偟偨偑偭偰栤戣乮俀乯偺摎偊偼丂傾亖係丄僀亖侾
夝摎丒偦偺10
乮儁儞僱亅儉丗揮埵斀墳乯
(1) 1丄2傑偨偼3抜栚偵丄乽0乿傪擖傟傞偲偦偺壓抜偵摨偠悢帤偑尰傟丄
戣堄傪枮偨偝側偄丅傛偭偰丄係抜栚偺悢帤偑侽偱偁傞丅
(2) 3(5+傾+僀)偺堦埵偑0偱偁傞偙偲
偐偮丄3亝(傾+僀)亝15 偱偁傞偙偲偐傜丄傾丄僀偼埲壓偺忦審傪枮偨偡丅
丂 3(5+傾+僀)=30 丒丒丒(1)
丂傑偨偼丄
丂3(5+傾+僀)=60丂丒丒丒(2)
丂丒働乕僗(1)丗 傾+僀=5
峫偊傜傟傞(傾,僀)偲偟偰丄(1,4)丄(2,3)丄(4,1)丄(3,2)
丂丂丂専徹偡傞偲丄(4,1)埲奜偼戣堄傪枮偨偝側偄
丂丒働乕僗(2)丗 傾+僀=15
峫偊傜傟傞(傾,僀)偲偟偰丄(6,9)丄(7,8)丄(8,7)丄(9,6)
丂 専徹偡傞偲丄壗傟傕戣堄傪枮偨偝側偄
傛偭偰丄傾=4丄僀=1
夝摎丒偦偺11
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂傾亖係丂僀亖侾丂偱偡丅
嘆乣嘔傑偱偺仩偺拞偵侽傪擖傟傞偲壓偺抜偺仩偵摨偠悢帤偑弌傑偡偺偱
侽偼巐抜栚偺嘔偵擖傝傑偡丅
嶰抜栚偺嘒嘓偺崌寁悢帤偑侽偵側傞慻崌偣偼師偺係僷僞乕儞偵側傝傑偡丅
俙丏俁偲俈丂丂俛丏俈偲俁丂丂俠丏俀偲俉丂丂俢丏俉偲俀
俙偲俛偺僷僞乕儞偼侽仺俁仺1仺俁偱俁偲偄偆摨偠悢帤偑偱傑偡偺偱懯栚偱偡丅
侽仺俈仺係傪擖傟偰専徹偡傞偲嵍偺俁仺係偲側傝摨偠悢帤偑弌傞偺偱懯栚偱偡丅
廬偭偰俉偲俀偑偁傞俠偲俢偺僷僞乕儞傪専徹偟傑偡丅
嶰抜栚偺嘒偵俉傪擖傟傞偲慡偰偺仩偵0乣俋傑偱偺堎側傞悢帤傪擖傟傞帠偑弌棃傑偡丅
嶰抜栚偺嘒偵俀傪擖傟傞偲摨偠悢帤偑弌棃傑偡偺偱懯栚偱偡丅
廬偭偰恾侾偺捠傝偺悢帤偺攝抲偲側傝摎偊偼傾亖係丂僀亖侾偑摎偊偵側傝傑偡丅
夝摎丒偦偺12
乮儁儞僱亅儉丗tt乯
(1)侾乣3抜栚偵0偑擖傞偲偡傞偲丄摨偠悢帤偑擇夞擖偭偰偟傑偆乮亖0偺椬偺悢帤
偲丄0偺壓偺悢帤偑摨偠偵側傞乯偺偱戣堄偵斀偡傞丅
廬偭偰丄0偑擖傞偺偼4抜栚偟偐偁傝摼側偄丅摎偊丂0
(暿夝:壓抜偺悢帤偼忋抜偺擇偮偺悢帤偺榓偺堦偺埵偺悢偱偁傞偑丄
榓偑擇寘偵側傞応崌偵廫偺埵偺悢帤傪巆偟偰偄偭偰丄嵟屻偵堦偺埵偺悢帤傪巆偟偰
傕
寢壥偼摨偠偵側傞丅偙偺惈幙傪棙梡偟丄堦抜栚偐傜壓抜偵岦偐偭偰丄
壛偊偨悢帤偺堦偺埵偩偗傪巆偡偺偱側偔
廫偺埵傕娷傔偨悢帤傪婰擖偟偰偄偔偲偡傞丅偦偺忋偱峏偵偡傋偰偺悢帤傪懌偡
偲丄榓偼
俋亄傾亄僀亄俇亄
乮俋亄傾乯亄乮傾亄僀乯亄乮僀亄俇乯亄
乮俋亄傾亄傾亄僀乯亄乮傾亄僀亄僀亄俇乯亄
乮俋亄傾亄傾亄僀亄傾亄僀亄僀亄俇乯
亖俋亊乮傾亄僀乯亄俇侽
偲側傞丅偙偺堦偺埵偺悢偼
幚嵺偵偼10屄偺仩撪偵0偐傜9傑偱偺悢帤偑堦偮偢偮擖偭偰偄傞偺偱偦偺憤榓
丂丂0+1+2+3+4+5+6+7+8+9=45
偺堦偺埵偺悢帤丄懄偪俆偱偁傞丅廬偭偰
9亊乮傾亄僀乯偺堦偺埵偑5偱偁傞偺偱丄乮傾亄僀乯偼5枖偼15偱偁傞丅
乮侾亝乮傾亄僀乯亝15側偺偱乯 (*)
4抜栚偺悢帤偼3亊傾亄3亊僀亄15亖3亊乮傾亄僀亄俆乯偺堦偺埵偺悢帤偱偁傞偲偙傠丄
乮傾亄僀乯偑俆枖偼15偱偁傞偙偲偐傜乮傾亄僀亄5乯偼10偺攞悢偵側傞丅埲忋偐傜丄
4抜栚偺悢帤偼0偱偁傞丅)
(2)忋婰 (*)偐傜丄傑偢擇抜栚恀傫拞偺仩偵擖傞悢帤乮(傾亄僀)偺堦偺埵偺悢帤)偼5
偲暘偐傞丅
偦偙偱乮傾亄僀乯偑5偱偁傞偐15偱偁傞偐傪峫偊傞偑丄15偱偁傞偲偡傞
偲丄乮傾丄僀乯亖乮俉丆俈乯枖偼乮俈丆俉乯
偺偳偪傜偐偺応崌偟偐偁傝摼側偄丅傾亖俉偱偁傞偲偡傞偲擇抜栚嵍偺仩偵偼俈偑擖傞
偑丄僀亖俈偱偁傞偙偲偐傜
廳暋偟偰偟傑偆偺偱晄壜丅傾亖俈偱偁傞偲偡傞偲擇抜栚嵍偺仩偵偼俇偑擖傞偑丄俇偼
婛偵堦抜栚偺堦斣塃偵
擖偭偰偄傞偺偱偙傟傕廳暋偑惗偠丄晄壜偱偁傞丅廬偭偰丄傾亄僀亖5偱偁傞丅偙傟傑
偱偵0,5,6,9偑偳偺仩偵偼偄傞偐
暘偐偭偰偄傞偺偱丄巆傞6偮偺仩偵1,2,3,4,7,8偑堦偮偢偮擖傞偙偲偵側傞丅偙傟傜俇
偮偺仩偵擖傞悢帤偼偦傟偧傟
堦抜栚乮傾丄僀乯丄擇抜栚乮乮傾亄俋乯偺堦偺埵偺悢帤丄乮僀亄俇乯偺堦偺埵偺悢
帤乯丄嶰抜栚乮乮傾亄俋亄俆丆懄偪傾亄侾係乯偺堦偺埵偺悢帤丄乮僀亄俇亄俆丄懄
偪僀亄侾侾乯偺堦偺埵偺悢帤乯
偲側偭偰偄傞偲偙傠丄擇抜栚嵍偼乮傾亅侾乯丄嶰抜栚塃偼乮僀亄侾乯偱偁傞丅埲忋
偐傜丄傾亄僀亖俆丄1亝傾亝係丄1亝僀亝係偱偁傝丄
偐偮丂僀丄乮僀亄侾乯丄乮傾亅侾乯丄傾偺係偮偺悢帤偑憡堎側偭偰偄傞昁梫偑偁
傞丅偙偺忦審傪枮偨偡偺偼
僀亖侾丄傾亖係丂埲奜偵偼側偔丄幚嵺偵寁嶼偟偰傒偰廫屄偺仩偵0乣9偑堦偮偢偮擖傞
偙偲傪妋擣偟偨丅
摎偊丗丂傾偼係丆僀偼侾丅
夝摎丒偦偺13
乮儁儞僱亅儉丗岼偺柌乯
 塃恾偺傛偆偵斣崋傪傆傝戣堄傪峫偊傞丅
塃恾偺傛偆偵斣崋傪傆傝戣堄傪峫偊傞丅
忦審傪惍棟偡傞偲丄0乣9偺悢偼奺乆1夞偟偐巊梡偱偒側偄丅
懄偪丄摨偠悢傪2夞巊梡偟偰偼偄偗側偄偺偱0偼嵟屻偺抜偱偟偐巊梡偱偒側偄偙偲偵側傞丅
場偭偰丄僋亖0偲側傞丅
偙傟傛傝丄(僇丄僉)偼乮2,丂8乯側偄偟乮3丄7乯偟偐側偄偙偲偑暘偐傞丅
崱丄僇亖8丄僉亖2偲偟偰傒傞偲丄
僂+僄亖1+7丄7+1丄3+5丄5+3偺偳傟偐偱偁傝丄僄+僆傕
奺乆偵懳偟丄
僄+僆亖7+5丄5+7偺偳偪傜偐偱偁傞丅懄偪丄
乮僂丄僄丄僆乯亖乮1,7,5乯側偄偟乮3,5,7乯偺偳偪傜偐偱偁傞丅
崱丄僂亖1偲偡傞偲丄傾亖2偲側傝僉偲摨偠抣偲側傞偺偱懯栚偱偁傞丅偦偙偱丄僂亖3偲偡傞偲丄
傾亖4偲側傞丅場偭偰丄傾亄僀亖4亄僀亖5傛傝僀亖1偲側傞丅僀+6亖1+6亖7亖僆偲側傝戣堄傪枮偨偡丅
懄偪丄偙傟偑媮傔傞傕偺偱偁傞丅
場偭偰丄傾亖4丄僀亖1偱偁傞丅
師偵(僇丄僉)亖乮2,丂8乯丄乮3,7乯偍傛傃乮7,3乯偺3働乕僗偵偮偄偰傕摨條側専摙傪峴偆偲丄慡偰柕弬偑惗偠偰偟傑偆丅
場偭偰丄慜婰夝摎偑媮傔傞傕偺偱偁傞丅
夝摎丒偦偺14
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
(1)係抜栚偺悢偼丄侽偱偡丅
侽偼壗偲懌偟偰傕偦偺悢傪曄壔偝偣側偄偺偱俁抜栚傑偱偵偁偭偰偼側傝傑偣傫丅
侾侽屄偺応強偵丄侾侽庬偺悢傪擖傟傞偙偲偑偱偒側偔側傝傑偡丅
(2)応崌偺悢偑偦傫側偵懡偔側偄偺偱忦審傪憹傗偟偰嫹傔偰偄偒傑偡丅
侾抜栚偺傾偲僀偵丄侽丆俇丆俋偑偙側偄偲偡傞偲
俈P俀亖俈亊俇亖係俀捠傝
偝傜偵俀抜栚偺椉抂偵侽丆俇丆俋偑偙側偄偙偲傪忦審偲偟偰壛偊傞偲
傾偵侽丆俁丆係傪丄僀偵侽丆侾丆俈傪梡偄側偄偺偱丄師偺俀俀捠傝偱偡丅
| 丂 | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 傾 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 5 | 5 | 5 | 5 | 7 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 |
| 僀 | 2 | 3 | 4 | 5 | 8 | 3 | 4 | 5 | 8 | 2 | 3 | 4 | 8 | 2 | 3 | 4 | 5 | 8 | 2 | 3 | 4 | 5 |
応崌偺悢偑懡偔側偄偺偱嬶懱揑偵彂偒弌偟偰傒傞偲丄
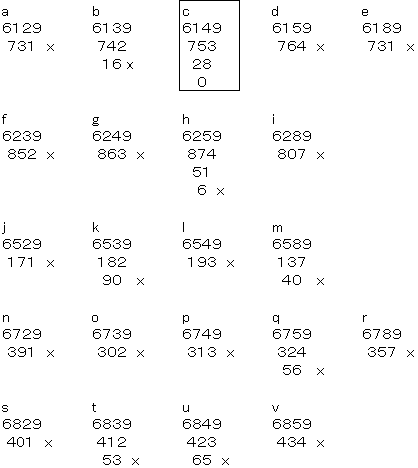
傾偼侾丄僀偼係偱偡丅
夝摎丒偦偺15
乮儁儞僱亅儉丗T_Tatekawa乯
(1) 4抜栚埲奜偵0偑擖傞偲丆偦偺偡偖壓偺仩偼椬偺悢帤偲摨偠偵側偭偰偟傑偆丏傛偭偰4抜栚偺仩偼0丏
(2) (1) 偐傜3抜栚偺仩偺榓偼10偱偁傞丏1抜栚偱6偲9偑巊傢傟偰偄傞偺偱丆 (2, 8) 偐 (3, 7) 偺慻傒崌傢偣丏
婏悢傪 o丆嬼悢傪 e 偲偟偰1抜栚偐傜暲傋偰傒傞丏
1抜栚偵婏悢偐嬼悢偺偄偢傟偐偑懙偆偲
9 o o 6 9 e e 6
e e o o o e
e o e o
偲側傝丆4抜栚偑0乮嬼悢乯偵側傜側偄偺偱僟儊丏
9 o e 6 9 e o 6
e o e o o o
o o e e
0 0
慜幰偺応崌丆嵍懁偑7偱側偄偲2抜栚偺 o 偵揔偟偨悢偑擖傜側偄丏
9 o e 6 9 o e 6
e o e e o e
7 3 3 7
0 0
塃懁偼丆2抜栚偺o傪1偵偡傞偲偦偺塃偑6側偺偱柕弬丏2抜栚偺o傪5偵偡傞偲偦偺塃偑2丏1抜栚偺6偺嵍傕6偵側傝柕弬丏
嵍懁偱2抜栚偺 o 傪 5 偵偡傞偲丆2抜栚偼廂傑傞丏
9 o e 6
2 5 8
7 3
0
偲偙傠偑偙傟偱傕1抜栚偑偩傔丏9 3 2 6 偱偼 2 偲 3 偑廳暋丏傛偭偰3抜栚偵栠傝丆(2, 8) 偺慻傪峫偊傞丏
1抜栚偺e偑巆傝偺 4 偵側傞丏
9 4 o 6 9 4 o 6
o o o o o o
2 8 8 2
0 0
9 4 o 6 9 4 o 6
3 o o 3 o o
2 8 8 2
0 0
嵍懁偼 3 偺椬偑 9 偵側傞偺偱柕弬丏巆傞摎偊偼
9 4 1 6
3 5 7
8 2
0
偱偁傞丏傾偼 4丆僀偼 1丏
夝摎丒偦偺16
乮儁儞僱亅儉丗偔偭偒乕侓乯
 乮侾乯侽
乮侾乯侽
乮俀乯傾亖係丄僀亖侾
峫偊曽丗
侾抜栚偼栤戣傛傝丄俋丄傾丄僀丄俇
俀抜栚傪嵍偐傜弴偵丄僂丄僄丄僆
俁抜栚傪嵍偐傜弴偵丄 僇丄僉
係抜栚傪 僋偲偟傑偡丅
婰崋乽佭乿傪乽侾侽偱妱偭偨偁傑傝偑摍偟偄乿偙偲傪堄枴偡傞偲偟傑偡
乮侾侽傪朄偲偡傞忚梋偲偄偆尵偄曽偱偄偄傫偱偟偨偭偗丅丅乯丅
乮侾乯
偨偲偊偽丄僂亖侽偲偟偰傒傞偲丄僇佭僂亄僄亖僄丅
偟偐偟側偑傜丄侾寘偺悢帤傪堦夞偯偮巊偆偲偄偆忦審偐傜丄
僇亖僄偼偁傝偊側偄丅
偟偨偑偭偰丄僂亗侽丅
摨條偵丄傾乣僉偼侽偱偼偁傝偊傑偣傫丅
寢嬊丄侽偑擖傞偙偲偑偱偒傞偺偼堦斣壓偺僋偺傒偱偡丅
乮俀乯
僇亄僉傪峫偊傑偡丅
僋佭僇亄僉偱丄
僋亖侽丄僇偲僉偼堦寘偺悢帤側偺偱丄僇亄僉亖侾侽丅
傑偨丄僇亄僉佭僂亄僆側偺偱丄僂亄僆佭侽丅
偙傟偲丄僂亄僆佭俋亄傾亄僀亄俇偐傜丄傾亄僀佭俆丅
傾亄僀佭俆傪枮偨偡傾偲僀偺慻傒崌傢偣偼丄
乮傾丄僀乯亖乮侾丄係乯丄乮係丄侾乯丄乮俈丄俉乯丄乮俉丄俈乯偺係捠傝丅
乮傾丄僀乯亖乮侾丄係乯偼丄僂佭傾亄俋佭侽偲側傝晄揔丅
乮傾丄僀乯亖乮俈丄俉乯偼丄僂佭傾亄俋佭俇偲側傝晄揔丅
乮傾丄僀乯亖乮俉丄俈乯偼丄僂佭傾亄俋佭俈亖僀偲側傝晄揔丅
徚嫀朄偱巆傞偺偼丄乮傾丄僀乯亖乮係丄侾乯偺慻傒崌傢偣丅
偦偟偰丄偙偺偲偒
乮傾丄僀丄僂丄僄丄僆丄僇丄僉丄僋乯亖乮係丄侾丄俁丄俆丄俈丄俉丄俀丄侽乯偲
側傝丄妋偐偵戣堄傪枮偨偡夝偑摼傜傟傞丅
[曗懌]乽僇亄僉佭僂亄僆乿偵偮偄偰
僇亄僉佭侽偱偁傝丄僇亗僉偩偐傜
僇佭俆亄兛丄僉佭俆亅兛偲偍偗傑偡乮僇佭俆亅兛丄僉佭俆亄兛偱傕摨偠乯丅
僇佭僂亄僄偐傜丄僂亄僄佭俆亄兛
僉佭僆亄僄偐傜丄僆亄僄佭俆亅兛佭俆亄乮侾侽亅兛乯
僄偼丄僂亄僄偲僆亄僄偵嫟捠偟偰偄傞場巕偩偐傜丄僄亖俆偲寢榑偟傑偟偨丅
偟偨偑偄傑偟偰丄僇亄僉佭僂亄僄亄僆亄僄佭僂亄僆亄侾侽佭僂亄僆偵側傝傑偟偨丅
夝摎丒偦偺17
乮儁儞僱亅儉丗柪巕偺梇擫乯
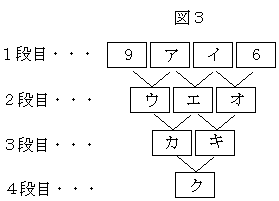
恾偺彙栚偵埲壓偺偲偍傝婰崋傪偮偗傞丅
侾抜栚嵍偐傜丄俋丄傾丄僀丄俇
俀抜栚嵍偐傜丄丂僂丄僄丄僆
俁抜栚嵍偐傜丄丂丂僇丄僉
係抜栚嵍偐傜丄丂丂丂僋
傾丄僀偺儅僗偺偄偢傟偐偑偑侽偩偲偡傞偲丄僂傑偨偼僆偺儅僗偑丄俋傑偨偼俇偵側偭偰偟傑偆丅
摨條偵丄僂丄僄丄僆丄僇丄僉偺儅僗偺偄偢傟偐偑偑侽偩偲偡傞偲丄
壓偺抜偺彙栚偺悢帤偑丄忋偺抜偺彙栚偺悢帤偲摨偠偵側偭偰偟傑偆偺偱丄
侾抜栚偐傜係抜栚傑偱偺10屄偺仩偺拞偵丄侽偐傜俋偺10屄偺悢帤偑侾偮偢偮擖傜側偔側偭偰偟傑偆丅
傛偭偰丄侽偼僋偺儅僗偵擖傞丅
僇丄僉偺慻傒崌傢偣偲偟偰偁傝偊傞偺偼
乮僇丆僉乯亖乮侾丆俋乯丆乮俀丆俉乯丆乮俁丆俈乯丆乮係丆俇乯丆乮俆丆俆乯丆
乮俋丆侾乯丆乮俉丆俀乯丆乮俈丆俁乯丆乮俇丆係乯
偱偁傞偑丄俋丆俇偼婛偵巊梡偝傟偰偄傞偺偱丄
乮僇丆僉乯亖乮俀丆俉乯丆乮俁丆俈乯丆乮俉丆俀乯丆乮俈丆俁乯
彙栚偺攝抲傛傝丄
乮俋亄傾乯亄乮傾亄僀乯亄乮僀亄俇乯亖僂亄僄亄僆丂乮mod 10乯
乮僂亄僄乯亄乮僄亄僆乯亖僇亄僉亖僋亖侽丂乮mod 10乯
乮俋亄傾乯亄乮傾亄僀乯亄乮僀亄俇乯亄乮傾亄僀乯亖侽丂乮mod 10乯
俁傾亄俁僀亄侾俆亖侽丂乮mod 10乯
俁乮傾亄僀亄俆乯亖侽丂乮mod 10乯
乮傾丆僀乯偺慻傒崌傢偣偲偟偰偁傝偊傞偺偼
乮傾丆僀乯亖乮侽丆俆乯丆乮侾丆係乯丆乮俀丆俁乯丆乮俁丆俀乯丆乮係丆侾乯丆
乮俆丆侽乯丆乮俇丆俋乯丆乮俈丆俉乯丆乮俉丆俈乯丆乮俋丆俇乯
偱偁傞偑丄侽丆俋丆俇偼婛偵巊梡偝傟偰偄傞偺偱丄
乮傾丆僀乯亖乮侾丆係乯丆乮俀丆俁乯丆乮俁丆俀乯丆乮係丆侾乯丆乮俈丆俉乯丆
乮俉丆俈乯
偱偁傞偑丄乮僇丆僉乯偺彙栚偵偼俀偐俁偺堦曽丄俈偐俉偺堦曽偼擖傞偙偲偐傜丄
乮傾丆僀乯亖乮侾丆係乯丆乮係丆侾乯
乮傾丆僀乯亖乮侾丆係乯偲偡傞偲
俋侾係俇 侽俆侽 丂俆俆 丂侽偲側偭偰悢帤偑廳暋偡傞丅
乮傾丆僀乯亖乮係丆侾乯偲偡傞偲
俋係侾俇 俁俆俈 俉俀 丂 侽偲側偭偰10屄偺悢帤偑侾偮偢偮擖傞丅
夝摎丒偦偺18
乮儁儞僱亅儉丗昹揷柧枻乯
(1) 侽
(2) 傾丗係丆僀丗侾
Option Explicit
'9 a b 6
' c d e
' f g
' h
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Dim a As Integer
Dim b As Integer
Dim c As Integer
Dim d As Integer
Dim e As Integer
Dim f As Integer
Dim g As Integer
Dim h As Integer
For a = 0 To 8
If a <> 6 Then
c = (9 + a) Mod 10
If c <> 6 And c < 9 And a <> c Then
For b = 0 To 8
If b <> 6 And a <> b And b <> c Then
d = (a + b) Mod 10
If d <> 6 And d < 9 And a <> d And b <> d And c <> d Then
e = (b + 6) Mod 10
If e <> 6 And e < 9 And a <> e And b <> e And c <> e And d <> e Then
f = (c + d) Mod 10
If f <> 6 And f < 9 And a <> f And b <> f And c <> f And d <> f And e <> f Then
g = (d + e) Mod 10
If g <> 6 And g < 9 And a <> g And b <> g And c <> g And d <> g And e <> g And f <> g Then
h = (f + g) Mod 10
If a + b + c + d + e + f + g + h = 0 + 1 + 2 + 3 + 4 + 5 + 7 + 8 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = a
Cells(Cells(1, 1).Value, 3).Value = b
Cells(Cells(1, 1).Value, 4).Value = c
Cells(Cells(1, 1).Value, 5).Value = d
Cells(Cells(1, 1).Value, 6).Value = e
Cells(Cells(1, 1).Value, 7).Value = f
Cells(Cells(1, 1).Value, 8).Value = g
Cells(Cells(1, 1).Value, 9).Value = h
End If
End If
End If
End If
End If
End If
Next b
End If
End If
Next a
End Sub
惓夝幰
| 僆儎僕 | teki | 偺偭偙傫 |
| 揮埵斀墳 | 僗儌乕僋儅儞 | falcon@拞妛嫵巘 |
| 柪巕偺梇擫 | 岼偺柌 | haya |
| 偔偭偒乕侓 | 忨偺偍偠偝傫 | 昹揷柧枻 |
| tt | 傗側偣 | T_Tatekawa |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | 嶰妏掕婯 | 僶儖僞儞惎恖 |
僐儊儞僩
haya偝傫偐傜師偺傛偆側儊乕儖傪偄偨偩偒傑偟偨丅
偲偙傠偱丄9 偲 6 偺惂栺傪奜偟偰丄PC偱夝傪専嶕偡傞偲丄拞搑敿抂偵 8 僷僞乕儞弌偰偒傑偡丅 嵍忋偺敔偵 1 乣 9 偺悢帤偑偦傟偧傟擖偭偰巒傑傝傑偡偑丄5 偱巒傑傞傕偺偑側偄偺偱偡丅 5 偼偳偺僷僞乕儞偱傕2抜栚偺拞墰偵偁偭偰丄 堦斣壓偺敔偑 0 偱側偗傟偽側傜側偄偺偲摨條側埖偄傪偡傋偒悢抣偲側偭偰偄傑偟偨丅
偦偙偑 5 偩偲傢偐偭偰偄傟偽榖偼傕偭偲娙扨偵側傞偺偱偡偑丄徹柧偱偒傑偣傫丅 巊偊傞悢帤偼婏悢5屄偲嬼悢5屄偱偡偐傜丄5 偑擖傞敔偑婏悢偵尷傞偙偲偼徹柧偱偒傞偺偱偡偑丒丒丒丅
偝傜偵丄栤戣偺敔傪戣堄偵増偭偰枮偨偡偵偼丄悢帤傪嬒摍偵偽傜嶵偔偙偲偑億僀儞僩側傛偆偱丄 惉棫偟偨僷僞乕儞傪尒傞偲丄壗傟傕堦抜栚偺崌寁偼 20丄擇抜栚偺崌寁偼 15丄嶰抜栚偺崌寁偼 10 偱偟 偨丅挌搙丄1 乣 9 偺暯嬒 5 偺屄悢攞偵側偭偰偄傑偡丅
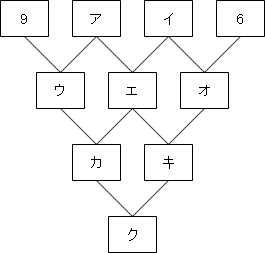
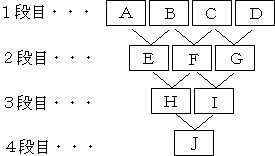 峫偊偰傒傑偟偨丅塃偺恾偺傛偆偵丄奺仩傪俙乣俰偲偟傑偡丅
峫偊偰傒傑偟偨丅塃偺恾偺傛偆偵丄奺仩傪俙乣俰偲偟傑偡丅
倃偲倄偺偦傟偧傟侾偺埵偑摍偟偄偲偒丄倃佭倄丂(mod 10)丂偲彂偔偙偲偵偟傑偡丅10偱妱偭偨忚梋偑摍偟偄偲偄偆偙偲偱偡丅
丂丂俤佭俙亄俛丂(mod 10)
丂丂俥佭俛亄俠丂(mod 10)
丂丂俧佭俠亄俢丂(mod 10)
丂丂俫佭俤亄俥佭俙亄俀俛亄俠丂(mod 10)
丂丂俬佭俥亄俧佭俛亄俀俠亄俢丂(mod 10)
丂丂俰佭俫亄俬佭俙亄俁俛亄俁俠亄俢丂(mod 10)
俰亖侽傛傝丄俰佭乮俙亄俢乯亄俁乮俛亄俠乯佭侽丂(mod 10)丒丒丒(1)丂偱偁傞丅
偙偙偱丄慡偰偺悢偺榓丂俙亄俛亄丒丒丒亄俰傪峫偊傞丅
丂丂俙亄俛亄丒丒丒亄俰
丂佭乮俙亄俛亄俠亄俢乯亄乮俤亄俥亄俧乯亄乮俫亄俬乯亄俰丂(mod 10)
丂佭俙亄俛亄俠亄俢亄乮俙亄俀俛亄俀俠亄俢乯亄乮俙亄俁俛亄俁俠亄俢乯亄乮俙亄俁俛亄俁俠亄俢乯丂(mod 10)
丂佭係乮俙亄俢乯亄俋乮俛亄俠乯丂(mod 10)
堦曽丄俙亄俛亄丒丒丒亄俰亖係俆偩偐傜丄
丂丂丂係乮俙亄俢乯亄俋乮俛亄俠乯佭俆丂(mod 10)丒丒丒(2)丂
(1)傛傝丄俁乮俛亄俠乯佭亅乮俙亄俢乯丂(mod 10)丂偱偁傞偐傜丄偙傟傪(2)偵戙擖偡傞偲丄
丂丂丂俙亄俢佭俆丂(mod 10)丒丒丒(3)丂
偙偺偲偒丄幃(1)傛傝丄俁乮俛亄俠乯佭亅俆佭俆丂(mod 10)丂偲側傝丄
偙傟傛傝丄俛亄俠佭俆丂(mod 10)偲側傞丅
俥佭俛亄俠佭俆丂(mod 10) 偱偁傝丄俥偼侾寘偺悢偩偐傜丄俥亖俆偲側傞丅
師偵丄抜偛偲偺悢偺榓傪峫偊偰傒傞丅
係抜栚偼丄俰亖侽
俁抜栚偼丄俫亄俬佭俰丂(mod 10)丄俰亖侽偱偁傝丄侾寘偺悢俀偮偺榓
偱偁傞偙偲傪峫椂偡傞偲丄俫亄俬亖侾侽
俀抜栚偼丄俤亄俥亄俧佭乮俙亄俢乯亄俀乮俛亄俠乯佭乮俙亄俢乯亄俀俥佭乮俙亄俢乯亄侾侽佭俆丂(mod 10)
侾寘偺悢俁偮偺榓偱偁傞偙偲傪峫椂偡傞偲丄俤亄俥亄俧亖侾俆
侾抜栚偼丄俙亄俛亄俠亄俢佭乮俙亄俢乯亄乮俛亄俠乯佭侽丂(mod 10)
侾寘偺悢係偮偺榓偱偁傞偙偲傪峫椂偡傞偲丄俙亄俛亄俠亄俢亖俀侽
 top
top