侾俆侾丏俉偮偺嶰妏宍偺柺愊
惓曽宍俙俛俠俢偼柺愊偑俋cm俀偱丄
惓曽宍俤俥俧俫偼惓曽宍俙俛俠俢偺偦傟偧傟偺曈傪俁摍暘偟偨揰傪捠偭偰偄傑偡丅
偙偺偲偒丄師偺奺栤偄偵摎偊側偝偄丅
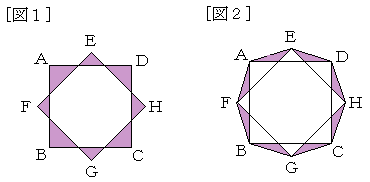
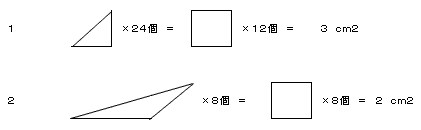
(1) [恾侾] 偱丄怓偺偮偄偨晹暘(俀偮偺惓曽宍傪廳偹偰偱偒偨俉偮偺嶰妏宍)偺柺愊偼壗cm偱偡偐丅
(2) [恾侾] 偺捀揰俙丄俥丄俛丄俧丄俠丄俫丄俢丄俤傪寢傫偩 [恾俀] 偱
怓偺偮偄偨晹暘(俉妏宍偲偺寗娫偵偱偒偨俉偮偺嶰妏宍)偺柺愊偼壗cm偱偡偐丅
栤戣偺弌揟
僙儞僗偺傛偄擼傪偮偔傞丂戝恖偺嶼悢僷僘儖
壨悾丂岤丂挊
帺桼崙柉幮
朙搰壀彈巕妛墍拞妛峑丒2006擭
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗傗側偣乯
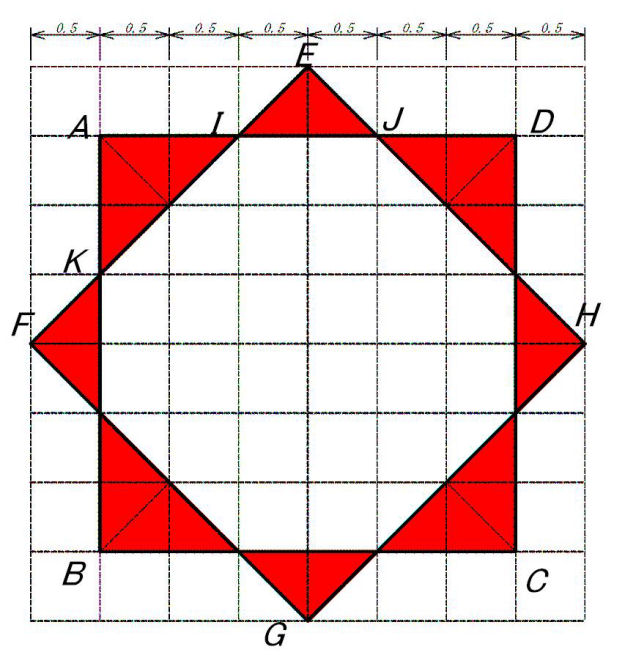
栤偄侾
恾傪0.5們倣娫妘偺彙栚偺忋偵昤偔偲旕忢偵夝傝傗偡偔側傝傑偡丅
彫偝側仮俤 俬 俰偺柺愊偼戝偒側仮俙 俲 俬偺柺愊偺敿暘偵側傞偺偑夝傝傑偡丅
戝偒側仮俙 俲 俬偺柺愊偼仩俙 俛 俠 俢偺柺愊偺1/18
偙傟偐傜彫偝側仮俤 俬 俰偺柺愊偼仩俙 俛 俠 俢偺柺愊偺1/36
偦傟偧傟偵係屄偯偮偁傞偺偱
仩俙 俛 俠 俢偺柺愊偺1/18亊係亄1/36亊係亖8/36亄4/36亖12/36亖1/3
摎偊丂丂丂俁 cm2
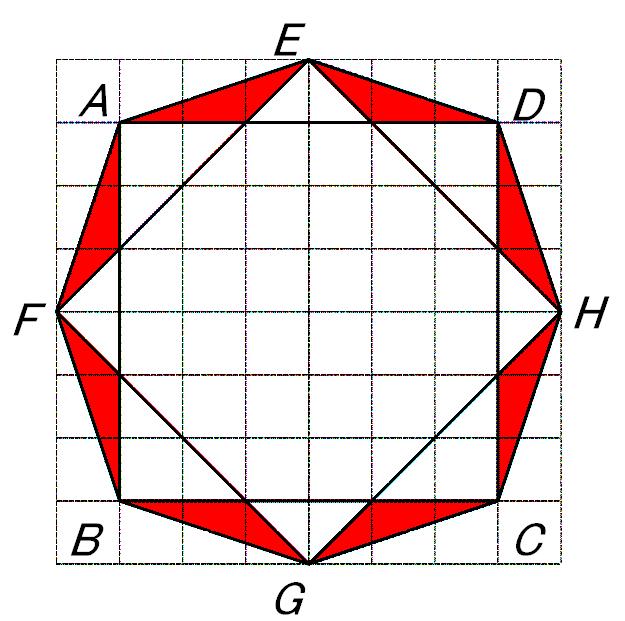
栤偄俀
仮俤 俬 俙偺柺愊偼掙曈偺挿偝偲崅偝偑仮俤 俬 俰偲摨偠側偺偱柺愊傕摨偠偵側傝傑偡丅
慡懱偱俉屄桳傞偺偱
仩俙 俛 俠 俢偺柺愊偺1/36亊8亖8/36亖2/9
摎偊丂丂俀 cm2
夝摎丒偦偺2
乮儁儞僱亅儉丗teki乯
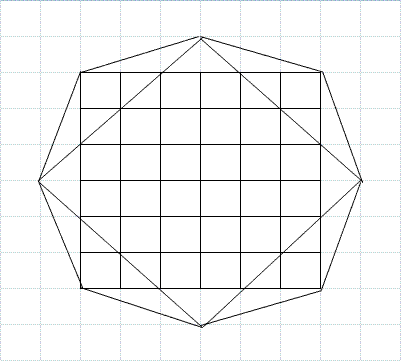
夝摎丒偦偺3
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
摎偊
丂侾乯俁
丂俀乯俀
峫偊曽丗
丂侾乯戝偒側嶰妏宍乮俙懠乯偼係屄偱丄堦曈侾偺惓曽宍偑俀屄偱偒傞丅
丂丂丂彫偝側嶰妏宍乮俤懠乯偼係屄偱堦曈侾偺惓曽宍偑侾屄偱偒傞丅
丂丂丂偁傢偣偰俁偵側傞丅
丂俀乯堦偮偺嶰妏宍偼掙曈侾丄崅偝偑彫偝側嶰妏宍俤偲嫟捠側偺偱柺愊偼摍偟偔側傞丅
丂丂丂侾乛係亊俉亖俀丂
夝摎丒偦偺4
乮儁儞僱亅儉丗偺偭偙傫乯
乮侾乯
俉屄偺嶰妏宍乮捈妏擇摍曈嶰妏宍乯偼師偺俀庬椶偵暘偗傜傟傞丂丂奺乆係屄偱偁傞
丂丂(i)戝偒偄曽丒丒丒捈妏傪偼偝傓曈偺挿偝偑侾
丂丂(ii)彫偝偄曽丒丒丒幬曈偺挿偝偑侾
(i)偲(ii)偺憡帡斾偼乮併俀乯丗侾丂丂傛偭偰柺愊斾偼俀丗侾
(i)偺柺愊亖侾/俀 偩偐傜丄(ii)偺柺愊亖侾/係
丂丂丂乮侾/俀乯亄乮侾/係乯亖俁/係 丂S亖乮俁/係乯丒係亖俁(cm2乯
乮俀乯
俉屄偺嶰妏宍偼偄偢傟傕乮侾乯偵偍偗傞(ii)偺柺愊偵摍偟偄偐傜
丂丂丂S亖乮侾/係乯丒俉亖俀乮cm2乯
夝摎丒偦偺5
乮儁儞僱亅儉丗僆儎僕乯
乮侾乯 恾侾偺係偮偺幬曈
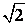 們倣偺捈妏俀摍曈嶰妏宍偺柺愊
丗係亊侾亊侾亐俀亖俀們倣俀丂丒丒乮嘥)
們倣偺捈妏俀摍曈嶰妏宍偺柺愊
丗係亊侾亊侾亐俀亖俀們倣俀丂丒丒乮嘥)
懠偺係偮偺幬曈侾們倣偺捈妏俀摍曈嶰妏宍偺柺愊丗係亊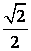 亊
亊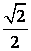 亐俀亖侾們倣俀丒(嘦乯
亐俀亖侾們倣俀丒(嘦乯
廬偭偰丂乮嘥乯丆乮嘦乯傛傝丂俀亄侾亖俁們倣俀丂丂丂丂丂丂丂丂丂丂亪丂俁們倣俀
丂丂
乮俀乯 恾俀偺俉偮偺嶰妏宍偼丄慡偰崌摨偱
堦曈偑丆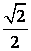 們倣丂
偲丂侾們倣丂嫴傑傟傞妏偑丂侾俁俆亱傛傝
們倣丂
偲丂侾們倣丂嫴傑傟傞妏偑丂侾俁俆亱傛傝
俉亊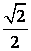 亊侾亊
亊侾亊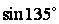 亐俀亖丂俀們倣俀丂丂丂丂丂丂丂丂丂丂亪丂俀們倣俀丂丂丂
亐俀亖丂俀們倣俀丂丂丂丂丂丂丂丂丂丂亪丂俀們倣俀丂丂丂
夝摎丒偦偺6
乮儁儞僱亅儉丗haya乯
(1) 3 cm2
(2) 2 cm2
亂夝偒曽亃
(1) 戝偒側嶰妏宍偼捈妏傪嫴傓擇曈偑 1cm 偱偁傞偐傜柺愊偼
丂丂丂 [(1 x 1)/2] x 4 = 2 cm2
彫偝側嶰妏宍偼幬曈偑 1cm丄捈妏傪嫴傓擇曈偑
 cm 側偺偱柺愊偼
cm 側偺偱柺愊偼
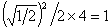 cm2
cm2
柺愊偺崌寁偼丄 2 + 1 = 3 cm2
(2) 仮EAD偼丄掙曈偑 3cm丄崅偝偑 1/2 cm 偩偐傜丄柺愊偼
丂丂丂 (3 x 1/2)/2 x 4 = 3 cm2
撪晹偺彫偝側敀偄嶰妏宍偺柺愊偼 (1) 傛傝 1 cm2 偩偐傜
柺愊偼丄3 - 1 = 2 cm2
夝摎丒偦偺7
乮儁儞僱亅儉丗ykak乯
1)丂俁 cm2
2)丂俀 cm2
峫偊曽
1)栤戣偺嶰妏宍偺偆偪戝偒偄傎偆偺嶰妏宍偼丄捈妏傪偼偝傓俀曈偺挿偝偑偳偪傜傕侾僙儞僠儊乕僩儖
偩偐傜丄俀摍曈嶰妏宍偱偁傝丄嶰妏宍偺捈妏偱側偄懠偺擇偮偺撪妏偼係俆搙偱偁傞丅
彫偝偄傎偆偺嶰妏宍偺捈妏偱側偄撪妏偼丄戝偒偄傎偆偺嶰妏宍偺係俆搙偺撪妏偲摨偠偩偐傜丄係俆搙偱丄
偙傟傕俀摍曈嶰妏宍偱偁傞
惓曽宍ABCD偱丄奺曈傪俁摍暘偟偨揰傪廲墶偵寢傫偱偱偒傞俋偮偺彫偝偄惓曽宍傪峫偊傞偲丄
偙偺惓曽宍偼侾曈偺挿偝偑侾偩偐傜丄柺愊偼侾 cm2 偱偁傞偑丄戝偒偄傎偆偺嶰妏宍偼丄忋偵弎傋偨偙偲偐傜
偙偺惓曽宍偺敿暘偺柺愊偱偁傞偙偲偑暘偐傞丅
傑偨彫偝偄傎偆偺嶰妏宍偼丄堦斣挿偄曈傪幉偵偟偰惓曽宍偺撪晹偵愜傝曉偟偰傒傞偲暘偐傝傗偡偄偑丄
彫偝偄惓曽宍偺柺愊偺係暘偺侾偵側傞丅
栤戣偺柺愊偼丄戝偒偄傎偆傕彫偝偄傎偆傕奺係屄暘偺柺愊偩偐傜丄俀暘偺侾亊係偲係暘偺侾亊係傪懌偟偰俁 cm2 偵側傞丅
2)栤戣偺嶰妏宍傪1)偺彫偝偄傎偆偺嶰妏宍偲斾傋偰傒傞丅惓曽宍偺曈AD傪嶰妏宍偺掙曈偲峫偊傞偲
栤戣偺嶰妏宍偲彫偝偄傎偆偺嶰妏宍偼丄掙曈偑偳偪傜傕侾偱丄崅偝傕偍側偠偱偁傞偐傜丄柺愊偼摍偟偄丅
摎偊偼嶰妏宍俉屄暘偺柺愊偩偐傜丄係暘偺侾亊俉偱俀 cm2 偲側傞丅
夝摎丒偦偺8
乮儁儞僱亅儉丗庴尡惗偺晝乯
(1) 8偮偺嶰妏宍偺偆偪丄捀揰A,B,C,D傪娷傓4偮傪崌傢偣傞偲堦曈偑1cm偺惓曽宍擇偮
偵側傝傑偡丅
巆傝偺4偮丄捀揰E,F,G,H傪娷傓傕偺傪崌傢偣傞偲堦曈偑1cm偺惓曽宍堦偮偵側傝傑
偡丅
傛偭偰
丂摎丂丗丂1亊1亊3亖3 cm2
(2) 8偮偺嶰妏宍偺堦偮丄椺偊偽捀揰A偲E傪娷傓傕偺偼丄恾侾偺捀揰E傪娷傓嶰妏宍偲
掙曈偑摨偠挿偝偱捀揰傪嫟桳偟偰偄傞偺偱丄摨偠柺愊偵側傝傑偡丅偙偺嶰妏宍偼4偮
崌傢偣傞偲堦曈偑1cm偺惓曽宍偵側傞偺偱丄8偮偱偡偲偦偺攞丄
偡側傢偪
丂摎丂丗丂2 cm2 偲側傝傑偡丅
夝摎丒偦偺9
乮儁儞僱亅儉丗柪巕偺梇擫乯
乮侾乯
惓曽宍俙俛俠俢偺柺愊偑俋cm2側偺偱丄惓曽宍俙俛俠俢偺堦曈偼俁cm
嶰妏宍俙偑捈妏擇摍曈嶰妏宍偵側傞偺偱丄捈慄俙俠偲捈慄俤俥偑係俆搙偱岎嵎偟偰偄傞丅傛偭偰丄
嶰妏宍俙丄俛丄俠丄俢偼崌摨偱丄捈妏傪偼偝傓堦曈偑侾cm偺捈妏擇摍曈嶰妏宍
嶰妏宍俤丄俥丄俧丄俫偼崌摨偱丄幬曈偑侾cm偺捈妏擇摍曈嶰妏宍
傛偭偰丄嶰妏宍俙丄俛丄俠丄俢傪俀偮慻傒崌傢偣傞偲堦曈偑侾cm偺惓曽宍偵側傞丅
嶰妏宍俤丄俥丄俧丄俫傪係偮慻傒崌傢偣傞偲堦曈偑侾cm偺惓曽宍偵側傞丅
恾侾偱丄怓偺偮偄偨晹暘偺柺愊偼俁cm2
乮俀乯
曈俙俢偺俁摍暘揰傪俲丄俴偲偡傞丅
俤偐傜曈俲俴偵悅慄傪堷偒丄悅慄偲曈俲俴偺岎揰傪俹偲偡傞丅
妏俤俲俹偲妏俤俴俹偑摍偟偔係俆搙側偺偱丄妏俲俤俹偲妏俴俤俹傕摍偟偔係俆搙丅
嶰妏宍俤俲俹偲嶰妏宍俤俴俹偼曈俤俹偑嫟捠偱丄
曈俤俲偲曈俤俴偺挿偝偑摍偟偄偺偱崌摨偱偁傞偺偱丄
堦曈偑侽丏俆cm偺捈妏擇摍曈嶰妏宍丅
嶰妏宍俙俲俤偼掙曈侾cm崅偝侽丏俆cm偺嶰妏宍偵側傞偺偱丄柺愊偼侽丏俀俆cm2
恾俀偱丄怓偺偮偄偨晹暘偺柺愊偼嶰妏宍俙俲俤偑俉偮暘偵側傞偺偱丄
柺愊偼俀cm2
夝摎丒偦偺10
乮儁儞僱亅儉丗T_Tatekawa乯
(1)
傑偢丆惓曽宍摨巑偑45搙偢傟偰偄傞帠傪妋偐傔傑偡丏
捀揰A傪娷傓怓偺偮偄偨嶰妏宍偼丆戣堄偐傜幬曈埲奜偺擇曈偺挿偝偑
摨偠偱偡丏
捀揰A偼捈妏側偺偱丆懠偺擇偮偺妏偼45搙偱偡丏
懳捀妏傪梡偄偰弴乆偵帵偟偰峴偔偲丆怓偺偮偄偨嶰妏宍偼
慡偰捈妏擇摍曈嶰妏宍偩偲暘偐傝傑偡丏
師偵曈AD偵拲栚偟傑偡丏
惓曽宍偺柺愊偑9 cm2 側偺偱丆惓曽宍偺堦曈偺挿偝偼3cm偱偡丏
曈偑嶰摍暘偝傟傞偲丆奺乆偺慄暘偺挿偝偼1cm偱偡丏
捀揰A, D 傪娷傓捈妏擇摍曈嶰妏宍偼堦曈偺挿偝偑1cm偱偡丏
捀揰E傪娷傓捈妏擇摍曈嶰妏宍偼丆幬曈偺挿偝偑1cm偱偡丏
傛偭偰丆捀揰A, B, C, D 傪娷傓捈妏擇摍曈嶰妏宍偺柺愊偼
丂丂(1 x 1) /2 = 1/2 cm2
捀揰E, F, G, H 傪娷傓捈妏擇摍曈嶰妏宍偺柺愊偼
丂丂(1 x 1/2) /2 = 1/4 cm2
偦傟偧傟4偮偢偮偁傞偺偱丆崌寁偺柺愊偼
丂丂(1/2 + 1/4) x 4 = 3 cm2
(2)
揰E偺幬曈偺挿偝偑1cm偱偁傞偺偱丆嶰妏宍ADE偺崅偝偼 1/2cm丏
傛偭偰丆媮傔傞柺愊偼
丂丂(((3-1)x 1/2)/2) x 4 = 2 cm2
夝摎丒偦偺11
乮儁儞僱亅儉丗挿嶈搰尨丂偐偑傒乯
俀偮偺惓曽宍偺侾曈偺挿偝偼堘偆傫偱偡偹丅偁傇側偄傾僽僫僀両
乮侾乯丂
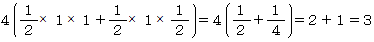
乮摎乯丂丂俁噋俀
乮俀乯丂幬慄晹偺侾屄暘偼
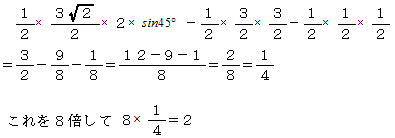
乮摎乯丂丂俀噋俀
夝摎丒偦偺12
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
(1)
丂丂丂(12/2)*4+(12/2)*(1/2)2*8=2+1=3 cm2
(2)
丂丂丂(12/2)*(1/2)2*2*8=2 cm2
偍傑偗丒丒丒恀傫拞偺惓曽宍(EFGH)偺柺愊偼(3+2*(1/2))2/2=8 cm2
偵側傞傫偱偡偹侓
夝摎丒偦偺13
乮儁儞僱亅儉丗揮埵斀墳乯
(1)俉偮偺嶰妏宍偼壓恾偺傛偆偵堏摦偱偒傞偺偱柺愊偼俁cm2
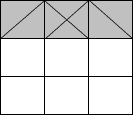
(2)怓偺晅偄偨嶰妏宍偺掙曈偲崅偝偼丄忋婰(1)偺彫偝偄嶰妏宍偺掙曈偲崅偝偲摍偟偄偺偱丄柺愊傕摍偟偄丅
傛偭偰丄媮傔傞柺愊偼俀cm2
夝摎丒偦偺14
乮儁儞僱亅儉丗岼偺柌乯

乮1乯惓曽宍ABCD偺堦曈偺挿偝傪3a偲偡傞偲丄
偦偺柺愊偑9 cm2 偱偁傞偐傜a2亖1偲側傞丅
4嬿偺嶰妏宍偺柺愊偼a2/2偑4屄側偺偱2 cm2
傑偨丄惓曽宍EFGH偺4嬿偺嶰妏宍偼幬曈偺挿偝
偑a偱偁傞偐傜柺愊偼a2/4偑4屄側偺偱1 cm2
偙傟傜傪壛偊偰丄媮傔傞傕偺偼3 cm2 偱偁傞丅
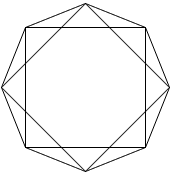
乮2乯8屄偺嶰妏宍偺崅偝偲掙曈偺挿偝偼惓曽宍
EFGH偵墬偗傞4嬿偺嶰妏宍偺柺愊偲摍偟偄偺偱丄
4屄偱1 cm2 丄8屄側偺偱2 cm2 偑媮傔傞傕偺偱偁傞丅
夝摎丒偦偺15
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
栤侾偺摎偊丂俁 cm2 偱偡丅
栤俀偺摎偊丂俀 cm2 偱偡丅
惓曽宍ABCD偺柺愊偑俋 cm2 側偺偱慄暘AJ = JI = ID = 1偲暘偐傝傑偡丅
栤侾丏
仮A偲仮B 偲仮C偲仮D偼摨偠柺愊側偺偱A偺柺愊傪媮傔偰係攞偡傞丅
掙曈妡偗傞崅偝妱傞俀側偺偱
丂丂丂乮侾亊侾乯/2 = 0.5亊4 = 2 cm2 丒丒丒(1)
仮E偲仮F偲仮G偲仮H偼摨偠柺愊側偺偱E偺柺愊傪媮傔偰係攞偡傞丅
仮E偺崅偝偼師偺曽掱幃偱媮傔傑偟偨丅Y = X - 1
X偵侾丏俆傪戙擖偡傞偲Y = 1.5-1 = 侽丏俆
廬偭偰E偺柺愊偼
丂丂丂乮1亊侽丏俆乯/2 = 0.25亊係 = 侾 cm2 丒丒丒(2)
丂丂丂(1)+(2) = 俀 cm2 亄侾 cm2 = 俁 cm2 偱偡丅
栤俀丏
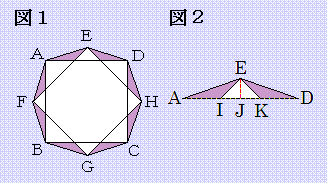
恾俀偼奼戝恾偱偡丅
慄暘AD偲EF偺岎揰傪I偲偡傞丅
慄暘AD偲EH偺岎揰傪K偲偡傞丅
捀揰E傛傝慄暘AD偵悅慄傪堷偒偦偺岎揰傪J偲偡傞丅
仮EAI偲仮EIK偺柺愊偼摍偟偄
掙曈丂AE = IK = 1噋
嶰妏宍偺崅偝偼慄暘AD偐傜E偺埵抲傑偱乮EJ乯側偺偱摨偠偱偡丅崅偝偼侽丏俆噋側偺偱柺愊偼
丂丂丂侽丏俆亊(1/2) = 侽丏俀俆
嶰妏宍偑俉屄偁傞偺偱
丂丂丂俉亊侽丏俀俆 = 俀 cm2
夝摎丒偦偺16
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
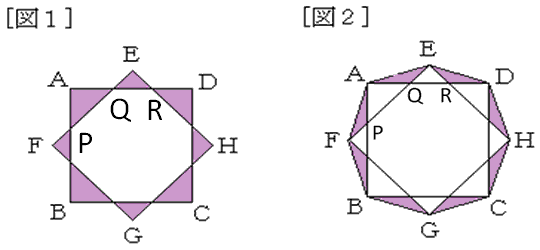
(1)
恾侾偵偍偄偰丄
仮APQ偲崌摨偱偁傞嶰妏宍偼係偮偁傝傑偡丅
仮APQ傪俀偮廤傔傞偲侾曈偺挿偝偑侾偺惓曽宍偵側傝傑偡丅
偩偐傜丄侾亊侾亊俀亖俀
仮EQR偲崌摨偱偁傞嶰妏宍偼係偮偁傝傑偡丅
仮EQR傪俀偮廤傔傞偲侾曈偺挿偝偑侾乛併俀偺惓曽宍偵側傝傑偡丅
偩偐傜丄(侾乛併俀)亊(侾乛併俀)亊俀亖侾
傛偭偰丄崌寁偺柺愊偼俁偱偡丅
乮俀乯
恾俀偵偍偄偰丄
仮AEQ偲崌摨偱偁傞嶰妏宍偼俉偮偁傝傑偡丅
AQ傪掙曈偲偟偨応崌丄崅偝偼侾乛俀偱偡丅
偩偐傜丄崌寁偺柺愊偼丄(侾乛俀)亊侾亊(侾乛俀)亊俉亖俀
夝摎丒偦偺17
乮儁儞僱亅儉丗嶰妏掕婯乯
亂夝摎亃
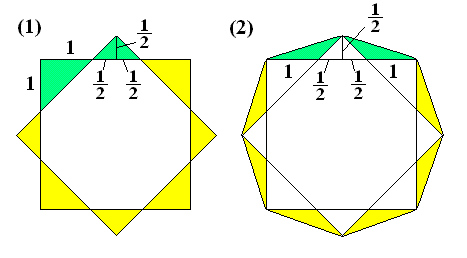
(1) 媮傔傞柺愊偼丆恾偺椢怓偺柺愊偺係攞丅
丂丂傛偭偰丆4亊{(1/2)丒1丒1亄(1/2)丒1丒(1/2)}亖2亄1亖3 cm2 乧(摎)
(2) 媮傔傞柺愊偼丆恾偺椢怓偺柺愊偺係攞丅
丂丂傛偭偰丆4亊(1/2)丒(1亄1)丒(1/2)亖2 cm2 乧(摎)
惓夝幰
| 挿嶈搰尨丂偐偑傒 | teki | 柪巕偺梇擫 |
| 庴尡惗偺晝 | 偺偭偙傫 | 岼偺柌 |
| 僗儌乕僋儅儞 | 揮埵斀墳 | ykak |
| 僆儎僕 | 忨偺偍偠偝傫 | 傗側偣 |
| haya | T_Tatekawa | 嶰妏掕婯 |
| 僶儖僞儞惎恖 | 栭傆偐偟偺偮傜偄偍偠偝傫 |
僐儊儞僩
(1)偵偮偄偰偼丄偡偖偵偍婥偯偒偺傛偆偵丄俉偮偺嶰妏宍偼戝偒偝偺堘偆俀庬椶偵暘椶偝傟傑偡丅
傑偨丄壗恖偐偺曽偐傜偛巜揈傪偄偨偩偄偰偄傞傛偆偵丄惓曽宍ABCD偲惓曽宍EFGH偼崌摨偱偼偁傝傑偣傫丅
偦偺偁偨傝偵拲堄偡傞昁梫偑偁傝傑偡偹丅
(2)偵偮偄偰偼丄懡偔偺恖偺夝摎偵偁傞傛偆偵丄嶰妏宍侾偮偺柺愊偑丄(1)偵搊応偟偨彫偝偄曽偺嶰妏宍偺柺愊偲摍偟偄
偙偲偐傜丄媮傔傞偙偲偑偱偒傑偡偹丅

 top
top