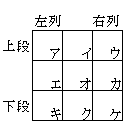
150.必勝法
下のアからケの9つのマスの中に、まもる君とたかし君が
1,3,4,5,6,7,8,9,10の9つの数字をどれか一つずつ順番に入れた後に、
まもる君は上段と下段の6つのマスの数の和を、
たかし君は左列と右列の6つのマスの数の和を計算し、
和の大きいほうが勝ちというゲームです。
まもる君から始めるとして、まもる君が必ず勝つためには、
はじめにどのマスにどの数を入れるとよいですか。
問題の出典
広中杯ハイレベル中学数学に挑戦
算数オリンピック委員会監修
講談社ブルーバックス
2001年トライヤル問題
答えと解説
解答・その1
(ペンネ−ム:スモークマン)
まもるくんとたかしくんとの得点の差は
イ+ク>エ+カ
になることを考えればよいので...
10-(9)-8-(7) と相手も最大になるように埋めていっても...10+8=18 > 9+7=16 で必
勝だと思ったけど...
そうか...相手につぎに自分のマスに1を入れられたら10+1で、2がないので、3を相手
のマスに入れても、3+9=12 で負けちゃうんだ!!
ならば...相手のマス(エ or カ)に1を放り込めばいいですね♪
そうすれば、、、相手は10を選ぼうが、11にしかならないので、自分のマスに9を入
れれば、相手は2を入れられないから3でも9+3=12 で勝てるんですね ^^v
おもしろかったです Orz〜
解答・その6
(ペンネ−ム:迷子の雄猫)
エまたはカのマスに1を入れる。
まもる君は上段と下段の6つのマスの数の和を、たかし君は左列と右列の6つの
マスの数の和を計算するのだから、まもる君、たかし君に共通するマスには、ど
んな数字が入っていても二人の差には関係がない。
よって、まもる君はイとクの2つのマスの数の和を、たかし君はエとカの2つの
マスの数の和を計算すると考えてよい。
まもる君にとっての初手、たかし君にとっての第2手について、2種類の戦略が
考えられる。自分が大きい数字を確保するか、相手に小さい数字を取らせるか、
である。
たかし君が第2手で、まもる君と同じ戦略を取ったとしたら、まもる君が勝つの
は明白なので、たかし君は第2手で、まもる君と逆の戦略を取ることにする。
1.まもる君が初手で、自分で大きい数字を確保した場合
| 手番 | まもる君 | たかし君 |
| まもる君 | 10 | (なし) |
| たかし君 | 10,1 | (なし) |
| まもる君 | 10,1 | 3 |
| たかし君 | 10,1 | 3,9 |
結果、まもる君11点、たかし君12点でたかし君の勝ち。
2.まもる君が初手で、相手に小さい数字を取らせた場合
| 手番 | まもる君 | たかし君 |
| まもる君 | (なし) | 1 |
| たかし君 | (なし) | 1,10 |
| まもる君 | 3 | 1,10 |
| たかし君 | 3,9 | 1,10 |
結果、まもる君12点、たかし君11点でまもる君の勝ち。
よって、まもる君が初手で、相手に小さい数字を取らせれば必ず勝てる。
解答・その7
(ペンネ−ム:のっこん)
ア、ウ、キ、ケはいずれにも関係し、オはいずれにも関係しない
よって先手にのみ関係するイ、クと後手にのみ関係するエ、カについてだけ考えればよい
先手が勝つための方針は次の2つ
1 (イ+ク)を大きくする
2 (エ+カ)を小さくする
方針1に従ってみる
先手 イ=10
この時、後手の最善手はク=1である
こうされると先手はエ=3とするしかないが ※2が欠けているので
カ=9とすれば後手の勝ち
よって方針1では勝つことができない
方針2に従ってみる
先手 エ=1
この時、後手の選択は次の2つ
1 カ=10
2 イ=3
選択1の時、イ=9とすれば先手の勝ち
選択2の時、ク=10とすれば先手の勝ち
結論 エ(またはカ)に1を入れれば先手が勝つ
解答・その13
(ペンネ−ム:バルタン星人)
答え
エまたはカに「1」を入れる。
考え方:
3−10は連続なので、一つ飛ばしの1を相手のみの場所(エまはカ)
に入れればよい。
次に相手が10を取っても、こちらは9を取り、3を与えられても
(3+9)−(10+1)=1だけ勝てる。
解答・その3
(ペンネ−ム:teki)
答え エ か カ に 1 を入れる。
まもる君とたかし君の合計数の差は、イ+ク−エ−カ ですので、これが正に
なるようにすれば、まもる君が勝ちます。
で、引く数をできるだけ小さくするために、エかカに1をいれるのが正着です。
実際、これ以外の手では、勝てません。(説明は長くなるので割愛します。)
解答・その8
(ペンネ−ム:T_Tatekawa)
まもる君の和にだけ影響があるマスはイとク,
たかし君の和にだけ影響があるマスはエとカです.
まもる君から始めるならば,イとクの和をエとカの和よりも大きく
すればいいのです.そのためにはイかクに10を入れるのではなく,
エかカに1を入れるという手を使います.
エかカに1を入れた次の手を考えます.
1) たかし君はエとカの残った方に10を入れるとします.すると,
エ+カ=11
です.その後にまもる君がイかクに9を入れると,残った数字で最小なのは
3なので,
イ+ク≧12>エ+カ
になって勝ちます.
2) たかし君が対抗してイかクに3を入れたとします.
すると,
2-a) まもる君がイとクの残った方に10を入れます.
この後で残った数字で最大のものは9です.
よって,
イ+ク=13>10≧エ+カ
になります.
2-b) まもる君がエとカの残った方に4を入れます.
この後で残った数字で最小のものは5です.
よって,
イ+ク≧8>5=エ+カ
になります.
いずれの場合もまもる君の勝ちが決定します.
よって,最初にエかカに1を入れるのが必勝法です.
解答・その9
(ペンネ−ム:オヤジ)
解答(エ)または(カ)に1を入れる。
∵
(1)
まもる君が、例えば(エ)に1を入れたとする、たかし君は(カ)に10を入れる
のがベスト、次にまもる君が、(イ)または(ク)に9を入れ、たかし君が(イ)または(ク)の
残りに3を入れると残り(ア),(ウ),(オ),(キ),(ケ)にそれぞれ
A,B,α,C,Dに何を入れても A+B+α+C+D=30
但し α=4,5,6,7,8 のいずれか
まもる君の和は、A+B+C+D+12=42−α
たかし君の和は、A+B+C+D+11=41−α

(2)
まもる君が、例えば(エ)に1を入れたとする,たかし君が(イ)または(ク)に3を入れたとしても まもる君が、
(イ)または(ク)の残りに10 さらにたかし君が,(カ)に9を入れ 残り(ア),(ウ),(オ),(キ),(ケ)にそれぞれ
A,B,α,C,Dに何を入れても A+B+α+C+D=30
但し α=4,5,6,7,8 のいずれか
まもる君の和は、A+B+C+D+13=43−α
たかし君の和は、A+B+C+D+10=40−α
従って まもる君が,(エ)または(カ)に1を入れると,必勝。
解答・その15
(ペンネ−ム:haya)
問題150 「必勝法」 の解は、
「最初に、相手の固有の得点圏である、
「エ」(または「カ」)に最小数の1を入力して相手の得点を妨害すること」
相手が残る「カ」に最大数の10を入力しても、3手目で自己の固有の得点圏である「イ」
(または「ク」)に残る最大数の9を入力すれば、次に相手が「ク」に入力できる最少数は3なので、
12:11で1点差で勝つことができる。
解答・その4
(ペンネ−ム:kiyo)
結局
イ+ク>エ+カ となればよい。
したがって、最初に相手の得点になるエリアである「エ」か「カ」に最小の1を書けばよい。
例えば、
| * | * | * |
| 1 | * | * |
| * | * | * |
| * | * | * |
| 1 | * | 10 |
| * | * | * |
| * | 9 | * |
| 1 | * | 10 |
| * | * | * |
| * | 9 | * |
| 1 | * | 10 |
| * | 3 | * |
解答・その16
(ペンネ−ム:三角定規)
<ア><ウ><キ><ケ>は共有なので,勝敗は <イ>+<ク>,<エ>+<カ> の大小で決まる。
勝つためには,相手の得点が自分の得点より低ければよい。よって,
・まもる君の初手は … 1 を (たかし君の得点となる) <エ> または <カ> に入れる。 ←[答]
たかし君が初手で 10 を選んでも <エ>+<カ>=1+10=11。
まもる君が第2手で 9 を選べば,後どのように進んでも <イ>+<ク>≧9+3=12 だから,まもる君の勝ち。
解答・その14
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
まもる君の合計をMとする。
たかし君の合計をTとする。
M=ア+イ+ウ+キ+ク+ケ
T=ア+ウ+エ+カ+キ+ケ
MとTの差をXとすると
X=(イ+ク)−(エ+カ)
この時にX>0ならばまもる君の勝ちになります。
まもる君がエかカに1を入れると
その一方に10を入れたとすると
たかし君がエかカに10を入れるとまもる君はイかクに9を入れれば残った方に3以上の数字が入るので
イ+ク>=9+3>11=エ+カ
でXの値は必ず正となります。
たかし君がエかカに10以外の数字を入れたとするとまもる君がイかクに10を入れれば良い。
イ+ク>10=1+9>エ+カ
まもる君はエかカのマスに1を入れると勝ちになる。
解答・その10
(ペンネ−ム:長崎島原 かがみ)
【まもる君】=ア+イ+ウ+キ+ク+ケ
【たかし君】=ア+エ+キ+ウ+カ+ケ
であり、題意を満たすには、
【まもる君】−【たかし君】=イ−エ+ク−カ>0
となればよい。
すなわち イ+ク>エ+カ・・・(1) である。
※しかも、2が無いわけで、小さい方から2個と大きい方から2個の、
1,3,9,10 を使用しても、12>11となり、引き分けになることはない。
そこで、意地悪く入れることにして、
1手目に【まもる君】は【たかし君】陣地の「エ」(または「カ」)に最小数1を入れると、
式(1)は イ+ク>1+カ・・・(2) となり、
2手目に【たかし君】が、【たかし君】陣地の「カ」(または「エ」)に最大数10を入れ、
式(2)は イ+ク>1+10 すなわち イ+ク>11・・・(3) となる。
残った数は、3,4,5,6,7,8,9だから、
3手目に【まもる君】が、【まもる君】陣地の「イ」(または「ク」)に9を入れると、
式(3)は 9+ク>11 すなわち ク>2・・・(4) となる。
よって、残った数、3,4,5,6,7,8のどの数を「ク」に入れても、式(4)は満たされる。
したがって、
(答)【まもる君】は、意地悪く、最初に「エ」(または「カ」)に最小数1を入れる。
解答・その11
(ペンネ−ム:巷の夢)
まさる君(Mと表す)の合計は、ア+ イ+ ウ+ キ+ ク+ ケ
たかし君(Tと表す)の合計は、ア+ ウ+ エ+ カ+ キ+ ケ
共通のア、ウ、キ、ケ以外2箇所の和の大小で勝負は決まる。
まさる君が先手であるので、エ+ カの合計がなるべく小さくなるような数をエかカに入れてしまえば良い。
そこで、以下の様に考える。
【1のケース】
・Mがエかカに一番小さな数1を入れる。
・Tがエとカの残りに10をいれた場合
・Mはイかクに9を入れる
・Tが残りの数のうち一番小さな3をイかカの残りにいれても
9+3=12>10+1=11でMの勝ち
・もしTが8をどこかにいれても
・Mはイかカの残りの数何をいれても11より大きくなり勝ち
【2のケース】
・Mがエかカに一番小さな数1を入れる。
・Tがエとカ以外に10をいれた場合
・Mはイかクに9を入れる
・Tが残りの数のうち何をいれても勝ち
即ち必勝法はエかカに1を入れれば良い。
解答・その2
(ペンネ−ム:転位反応)
ア、ウ、キ、ケは二人に共通のマス、オは計算には
無関係なので、エまたはカの何れかに最小の数字
である1を入れれば良い。
そうすれば、常にイ+ク>エ+カが成立する。
解答: まもる君は、エまたはカに1を入れると良い。
解答・その12
(ペンネ−ム:受験生の父)
まもる君の得点 ア+イ+ウ+キ+ク+ケ (1)
たかし君の得点 ア+エ+キ+ウ+カ+ケ (2)
(1)-(2)= (イ+ク)-(エ+カ)
なので、まもる君が勝つためには (イ+ク)>(エ+カ)となるようにすればよい。
先手のまもる君がエに1を入れれば、たかし君が(エ+カ)を最大にするためにカに
10を入れ(エ+カ)=11としても、次にまもる君がイに9を入れれば、クに入る数字は
3以上8以下(残り札)となり
(イ+ク)≧12>11=(エ+カ)
となるので、勝つ。
エとカは入れ替えても同じことなので、
答: エ又はカに1を入れる
解答・その5
(ペンネ−ム:くっきー♪)
必勝手)エまたはカに「1」
考え方)
たかし君の得点は、ア+エ+キ+ウ+カ+ケ
まもる君の得点は、ア+イ+ウ+キ+ク+ケ
なので、
まもる君の得点とたかし君の得点の差は、(イ+ク)−(エ+カ)
つまり、
条件A)イ+ク>エ+カであれば、他のマス目の数字が何であってもまもる君の勝ち
また、与えられた数字は、1、3、4、5、6、7、8、9、10なので、
最小の組み合わせは、1+10=11。
つまり、
条件B)エとカに1と10を書いたら、あとはどう転んでもまもる君の勝ち。
そこで、2つの条件AとBとを考慮して、
1回表まもる君の攻撃はエに1を入れてみます(カに入れても同じ)。
1回表 エ−1(エに1を書き込むことをあらわします。以下同様)
1回裏 たかし君の攻撃で場合わけ。
A)10を使う場合
A−1)イ−10、またはク−10
→2回表、カ−9。
この時点でイ+ク>10=エ+カとなるので、まもる勝利。
A−2)カ−10
→エ+カ=11となり、たかし自滅
A−3)イ、ク、カ以外に10
→2回表、イ−9。
この時点でイ+ク>9、エ=1、8>カなので、エ+カ<9.まもる勝利。
B)10を使わない場合
B−1)カに10以外の数を入れる(2回表のカ−10を阻止する)
→2回表、イ−10。この時点でイ+ク>10≧エ+カとなるので、まもる勝利。
B−2)上記以外
→2回表、カ−10。イ+カ=11となり、たかし敗北。
以上、1回表でエ−1とすれば、まもる必勝です。
解答・その17
(ペンネ−ム:夜ふかしのつらいおじさん)
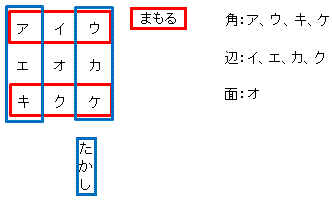
要点は、自分だけに関係する辺の「イ・エ・カ・キ」の攻防です。
考え方は、
(1)自分の得点を多くする。
(2)相手の得点を低くする。
条件は、
○使う数の差が均一でない。
です。
数が、「1・3・4・5・6・7・8・9・10」の9個なら
まもるは、1手目にたかしの辺のエかカに1を入れます。
たかしが、残りのたかしの辺に10を入れるとすると、
まもるは、まもるの辺のイかクに9を入れます。
すると、あとはどうやってもまもるの勝ちになります。
得点差が一番小さいのは、まもるの残りの辺に3が入る場合です。
使う数の差が均一でないためにこの場合でもまもるが1点勝ります。
数が、「1・2・3・4・5・6・7・8・10」の9個なら
まもるは、1手目にまもるの辺のイかクに10を入れます。
たかしが、残りのまもるの辺に1を入れるとすると、
まもるは、たかしの辺のエかカに2を入れます。
すると、あとはどうやってもまもるの勝ちになります。
得点差が一番小さいのは、たかしの残りの辺に8が入る場合です。
使う数の差が均一でないためにこの場合でもまもるが1点勝ります。
正解者
| バルタン星人 | スモークマン | haya |
| 転位反応 | くっきー♪ | オヤジ |
| 夜ふかしのつらいおじさん | teki | 長崎島原 かがみ |
| のっこん | 巷の夢 | kiyo |
| 杖のおじさん | 迷子の雄猫 | T_Tatekawa |
| 三角定規 | 受験生の父 |
コメント
このような場合、大きい数字を自分の側に確保したいと考えがちですが、
たかし君の側に一番小さい数字を入れ込んでしまいます。
一度入れた数字は、変えられませんから、たかし君はどうすることもできず、結果的にまもる君の勝ちとなります。
逆転の発想ですね。
用意された数字が連続しているようですが、「2」だけないことにお気づきでしょうか。
夜ふかしのつらいおじさんの解答にもあるように、
ここがもうひとつのポイントです。
 top
top