Weekend Mathematics／問題／問題15

１５．直方体の問題

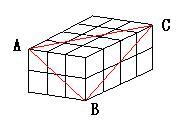
（１）下の図のように小さな立方体を縦３個、横４個、高さ２個 積み重ねて直方体ができています。 この直方体を、Ａ、Ｂ、Ｃの３つの点を通る平面で切りました。 小さな立方体のうち何個が切られましたか。

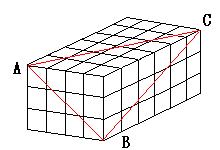
（２）今度は６×４×３に積み上げて直方体を作ります。 この直方体を、Ａ、Ｂ、Ｃの３つの点を通る平面で切りました。 小さな立方体はいくつ切られるでしょうか

何もわざわざスライスしなくても 　そのまま作図をすれば答がでます。
（１）については左の図参照。
答え　１２個

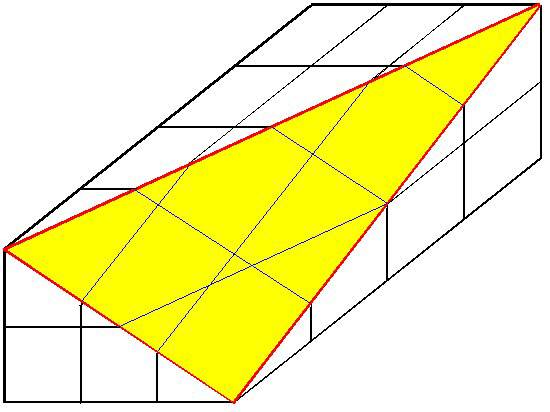
直線ＡＢ，ＢＣ，ＣＤ（赤い線）が それぞれ小さな立方体の辺と交差する点を直線（青い線）で結び 黄色い面の青い線で仕切られた数を数えれば答はでます。 一目瞭然です。
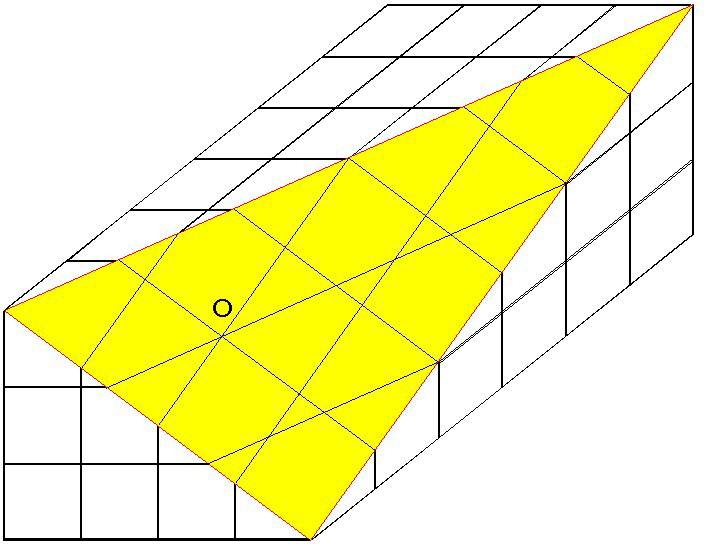
（２）は２４個ですがよく見ると１ヶ所３本の直線が交差する 点Ｏがあります。
もしこれが１点で交わらなければ ここに小さな三角形ができ２５個となります。

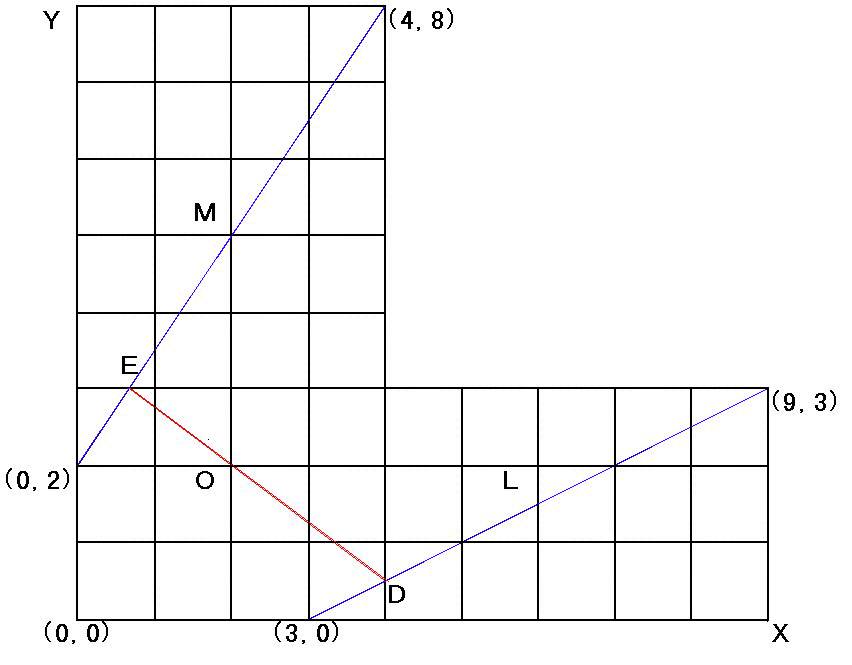
点Ｏで３本の直線が交わっていることの証明

手前の６個の立方体を取り除いた平面がこの図です。

Ｘ，Ｙ座標で考えると
　　直線Ｌは（３，０）（９，３）を通るので
　　　　　Ｙ＝（１／２）Ｘ−（３／２）・・・（イ）
　　直線Ｍは（０，２）（４，８）を通るので
　　　　　Ｙ＝（３／２）Ｘ＋２・・・・・・・（ロ）　となる
　　点Ｄの座標　　（イ）にＸ＝４を代入し　Ｙ＝１／２　　　（４，１／２）
　　点Ｅの座標　　（ロ）にＹ＝３を代入し　Ｘ＝２／３　　　（２／３，３）
　　よってＤ，Ｅを通る直線は　　Ｙ＝（−３／４）Ｘ＋（７／２）　となる
　　ここでＸ＝２の時　Ｙ＝２となり　点Ｏで交わる。

以上３つの図についても、ご本人の提供です。

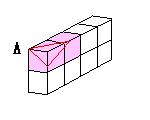
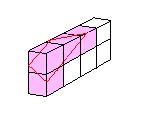
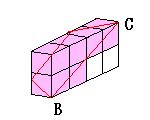
３列それぞれについて考える。
図より、１２個の小さな立方体が切られた。

立体を考えるのは、なかなかむずかしいですよね。
そこで、水平に１段ずつ分けてみました。
上面を通過する線と下面を通過する線を赤でかきました。
これをつなぐ面が切断面となるわけです。
切られる立方体を黄色でぬってあります。

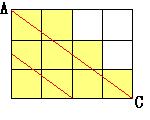
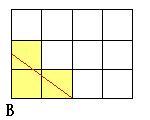
（１）については１２個の立方体が切られます。

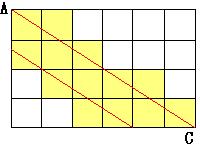
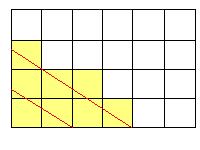
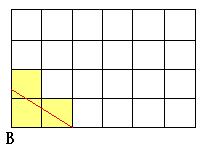
（２）については２４個の立方体が切られます。
立体のまま考えようとせず、平面にわけて考えるのがコツですね。

戻る