問題149　観覧車の問題

１４９．観覧車の問題

14分で一周する、直径が40メートルの観覧車がある。地上から30メートル以上のところから見える景色を「すばらしい景色」ということにすると、この観覧車で１周する14分間のうち、「すばらしい景色」が見られるのは何分何秒か。ただし、観覧車のゴンドラは直径40メートルの円周上を動くものとし、この観覧車の一番高い地点は地上40メートルであるとする。また、ゴンドラは一定速度で動くものとする。

問題の出典

広中杯ハイレベル中学数学に挑戦
算数オリンピック委員会監修
講談社ブルーバックス
2006年トライヤル問題

答えと解説

解答・その1

（ペンネ－ム：BossF）

14/3[m]=4’40”

解答・その2

（ペンネ－ム：真夏のサンタ）

今月の問題をやってみました。
図がかけないのですが、上の１２０°の間がいい景色ということになるので、４分４０秒！　

解答・その3

（ペンネ－ム：スモークマン）

地上から３０mのところは、半径の真ん中なので、正三角形２個分の角度＝１２０度から、 14/3=4+2/3=4分40秒は素晴らしい景色が見えるハッピータイムとなりますね♪

解答・その4

（ペンネ－ム：赤影）

答えは４分４０秒でしょうか？
以下、考え方です。
テキストのみで書くので分かりにくいかもですが、、、、、、、

観覧車の中心をＯ、真横から見て最初に高さ３０ｍに達する円周上の点をＡ、次に高さ３０ｍに達する円周上の点をＢとします。
題意は、弧ＡＢ（短い方）を移動する時間を求めることになります。
そのためには、角ＡＯＢの角度が分かれば、
　　１４分×（その角度／３６０度）で求められます。・・・・・・(1)
そこで、角ＡＯＢを求めます。
ここで、線分ＡＢの中点をＣとすると、三角形ＡＯＣは角Ｃを直角とする直角三角形になります。
　　ＡＯ＝観覧車の半径＝２０ｍ
　　Ｃ０＝点Cの地上からの高さ－観覧車の半径＝３０ｍ－２０ｍ＝１０ｍ
よって、
　　ＡＯ：ＣＯ＝２０：１０＝２：１
このことから、角ＡＯＣは６０度と分かります。
ゆえに角ＡＯＢ＝２×角ＡＯＣ＝１２０度
これを式(1)に代入すれば、求める答えは
　　１４分×（１２０／３６０）＝１４×６０秒÷３＝１４×２０秒＝２８０秒＝４分４０秒
が答えとなると思います。

解答・その5

（ペンネ－ム：迷子の雄猫）

観覧車の中心をＯ，頂上をＴ，地上からの高さが３０ｍである地点をＰ，Ｑ，直線ＯＴ上で、高さが３０ｍである地点をＨ，とする。
題意より、ＯＰ＝ＯＴ＝２０ｍ、ＯＨ＝ＨＴ＝１０ｍ
角ＯＨＰ＝角ＴＨＰ＝９０度であるので、三角形ＯＨＰと、三角形ＴＨＰは合同
ＴＰ＝２０ｍとなるので三角形ＯＴＰは正三角形となり、角ＰＯＴは６０度、角ＰＯＱは１２０度、となる。
ゴンドラは一定速度で移動するのであるから、ゴンドラが円弧Ｐ～Ｑ間を移動するのにかかる時間は、
全体の１２０／３６０＝１／３
１４分の１／３は２８０秒つまり４分４０秒

答え：４分４０秒

解答・その6

（ペンネ－ム：のっこん）

直径４０mの円の中心をO、地上から３０mの地点の１つをAとする
Oを通り地面に平行な直線を引き、Aからこの直線に下した垂線の足をHとすると
OA＝20(m)、AH＝10(m)となる　　　よって∠AOH＝30°
「すばらしい景色」が見られるのは３６０度のうちの120度、つまり１/３
１４（分）/３＝４分４０秒

解答・その7

（ペンネ－ム：バルタン星人）

答え
１４／３分＝４分４０秒

考え方：
観覧車の上半分を考えると、半径２０ｍの半円の高さ１０ｍ以上の部分。
２０：１０の直角三角形の挟角は６０度なので、１０ｍ以上の部分は１２０度で全周の１／３

解答・その8

（ペンネ－ム：teki）

答え　　４分４０秒

地上から３０ｍ以上の地点から「素晴しい景色」が見られるのですから、半径２０ｍの円の上部１０ｍ（この表現は適当ではないですが）が該当部分です。
半径が２０ｍなので、中心と弦が成す角は１２０度（１：２：√３の三角形、（小学生が解くとすれば、正三角形の半分と説明すればいいですね）が２つくっついた形なので６０＋６０＝１２０度）です。つまり円周の３分の１が該当する部分になります。
１周１４分なので、「素晴しい景色」が見られるのは、１４/３分＝４分４０秒です。

解答・その9

（ペンネ－ム：T_Tatekawa）

観覧車の直径40メートルなので，半径20メートル．観覧車の軸を原点にして x, y 軸を取り，x 軸と観覧車のゴンドラがなす角を s とする．

　　30 = 20 + 20 * 0.5 = 20 + 20 * sin(s)

となる s を考えると，30 度と 150 度．
ゴンドラが30メートル以上の高さにいるのは，全体に対して

　　(150-30)/360 = 1/3

である．1周が14分なので，

　　14 * 60 * 1/3= 280 秒 = 4分40秒

の間は，「すばらしい景色」が見られる．

解答・その10

（ペンネ－ム：ykak）

答え　４分４０秒

【考え方】
まずゴンドラの中心をＯ、ゴンドラが最高の高さに達した点をＡとする。
またゴンドラが最高点から下りはじめて高さが３０メートルの位置に達した点をＢとし、中心Ｏと点Ａを結んだ直線上の真ん中の点をＣとする。
中心Ｏは直径４０メートルのゴンドラの中心だから、地上からの高さ２０メートルの位置にあり、また点Ｏは最高点だから地上から４０メートルの位置にある。そうすると、点ＣはＯとＡを結んだ直線上で地上からの高さが３０メートルの位置にあることになる。
次に、点Ｃは直線ＡＯの中点だから、直線ＡＣと直線ＣＯの長さはそれぞれ１０メートルで等しく、また点Ｂも点Ｃも地上から３０メートルの高さにあるから直線ＢＣは地表の線と平行であり、したがって直線ＡＯと直線ＢＣは直角に交わる。
以上のことから、上記の点のうちＡＢＣを頂点とする三角形とＢＣＯを頂点とする三角形は合同であることが分かる。なぜなら、＜ＡＣＢ（直線ＡＣと直線ＢＣのなす角度をこう書くとする）＜ＢＣＯはともに９０度、また直線ＡＣと直線ＣＯの長さは等しく、直線ＢＣは二つの三角形に共通だからもちろん長さが等しい。ということで、一つの角とそれを挟む２辺の長さが等しいということになり、二つの三角形は合同であると言える。
そうすると直線ＡＢの長さは直線ＢＯの長さと等しいということになるが、ＢＯはゴンドラの円の半径であるから長さは２０メートルであり、ＡＢの長さも２０メートルである。
結局、直線ＡＯ、直線ＢＯ、直線ＡＢの長さはいずれも２０メートルということになるからこれらの直線で作られる三角形ＡＢＯは正三角形である。そうすると＜ＡＯＢは６０度であることが分かる。
ゴンドラの円周上で点Ａから点Ｂまでは地上から３０メートル以上の高さにあり、その円周上の長さは全体の６分の一である（３６０度　÷　６０度）。
ゴンドラの円周上で点Ａを中心として点Ｂと対称な位置を点Ｄとすれば、円周上の点Ａから点Ｄまでの間も同様に地上から３０メートル以上の高さにあるから、全体では６分の１の２倍、すなわち円周の長さの３分の１の間が地上から３０メートル以上の高さにあるということになる。
ゴンドラは等速で１４分かかって１周するから、答えはその３分の１の時間、すなわち４分４０秒ということになる。

解答・その11

（ペンネ－ム：オヤジ）

１４分＝１４×６０＝８４０秒　で一周するから，角速度を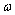とすると８４０＝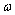
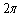
従って　
　　　
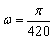
観覧車のゴンドラの高さを　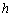　とすると，　
　　　
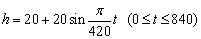
「すばらしい景色」となるのは、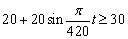　より
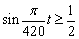　　　　を解くと
　　　
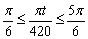
すなわち
　　　
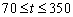
従って　求める時間は，３５０－７０（秒）＝２８０秒＝４分４０秒　∴　４分４０秒　　　　　　　　　　

解答・その12

（ペンネ－ム：haya）

問題149 観覧車の問題の解は 4分40秒です。

【解き方】
観覧車の円の軌跡の中心に直交座標の原点を置き、高さ 30m 以上となる角度を y = 10 を弦とする交点として求める。

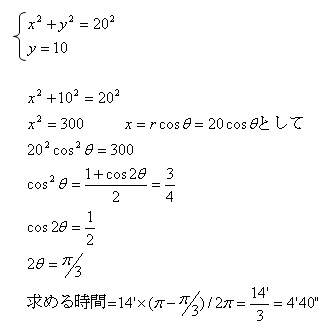
解答・その13

（ペンネ－ム：三角定規）

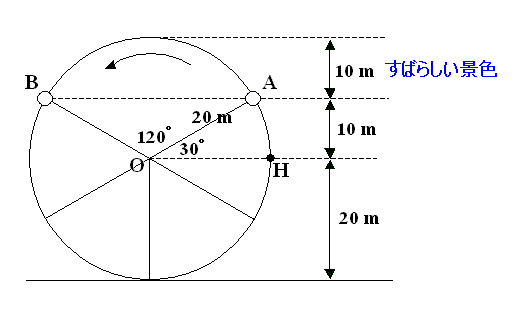
「すばらしい景色」が見えるのは，ゴンドラが図の劣弧AB上にあるときである。
題意から∠AOH＝30°，∠AOB＝120°で，これは１周の 1/3。
よって，「すばらしい景色」が見えるのは，14分/3＝4分40秒 …［答］

解答・その14

（ペンネ－ム：杖のおじさん）

答え　４分４０秒です。

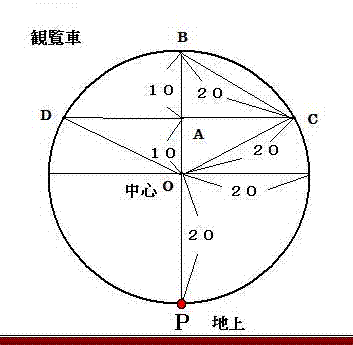
図の説明
観覧車の中心をＯ、一番高い地点をＢ、線分ＯＢの中点をＡとしてＡから水平に線を引いて円周との接点をＣ、Ｄ、観覧車の一番低い地点をＰとする。
△ＯＢＣは一辺を２０mとする正三角形です。従って∠BOC＝∠OBC＝∠BCO＝∠BOD＝６０°
∠COD＝６０°＋６０°＝１２０°
３６０°回転（一周）するのに１４分かかりますが地上から３０ｍ以上が「すばらしい景色」なので次の式で計算できます。
１４分＝８４０秒
８４０秒×１２０°/３６０°＝２８０秒/６０秒＝４分４０秒

解答・その15

（ペンネ－ム：長崎島原　かがみ）

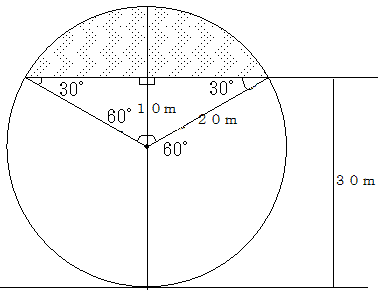
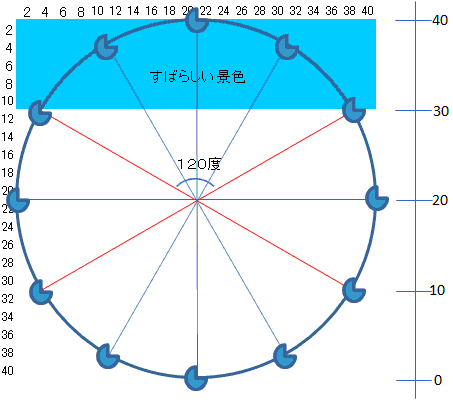
下図において、網掛け部分が「すばらしい景色」となり、１２０°分になる。
したがって、１４分の３分の１だから４分４０秒である。
（答）４分４０秒

解答・その16

（ペンネ－ム：巷の夢）

題意より観覧車の関係図は以下の様になる。即ち弧ABの短い方にあれば、最高の景色を望見できる。∠AOBが120°と全周角の1/3であるから14分の1/3が求めるもので、 4分40秒となる。図形的な説明は以下に示す。

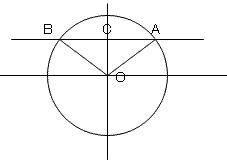
OA＝20ｍ、OC＝10ｍ、∠ACO＝90°であるから△ACOは直角三角形であり長さの比から ∠AOC＝60°となる。因って∠AOB＝120°である。

解答・その17

（ペンネ－ム：転位反応）

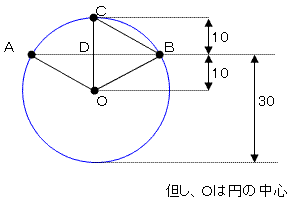
求める時間は、弧ＡＢをゴンドラが通過するのに要する時間に等しいので、中心角∠ＡＯＢを求めれば良い。
△ＢＣＤと△ＢＯＤにおいて、
ＣＤ＝ＯＤ＝１０、ＢＤは共通、∠ＢＤＣ＝∠ＢＤＯ＝９０°なので、
二辺とその挟角が等しいことから、
△ＢＣＤ≡△ＢＯＤ
従って、
ＢＯ＝ＣＯ＝ＢＣ＝２０（半径）であることから△ＢＯＣは正三角形
つまり、∠ＢＯＣ＝６０°であることから、∠ＡＯＢ＝１２０°
よって、１４分 × １２０／３６０＝４分４０秒

解答・その18

（ペンネ－ム：やなせ）

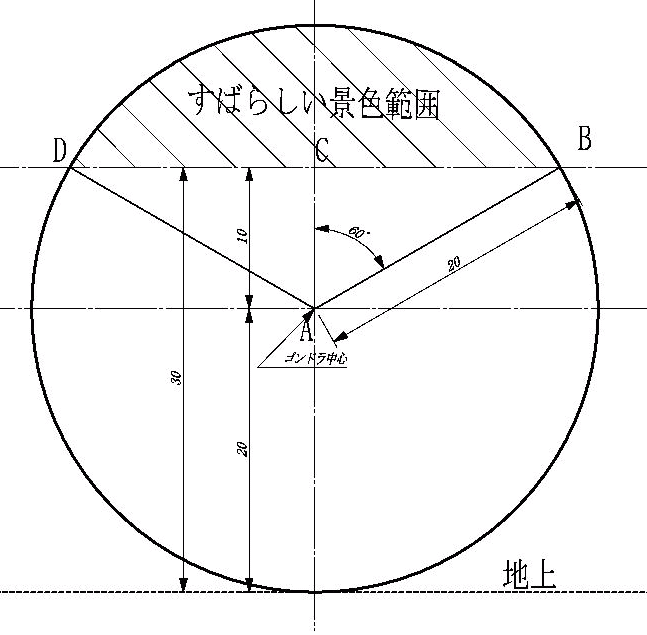
与えられた条件からゴンドラ中心Aからすばらしい景色ラインＤＢの中点Ｃまでは１０ｍ同じく中心ＡからＢまでは２０ｍになります。つまり、三角形（Ａ、Ｃ、Ｂ）はピタゴラスの定理に当てはまる
　ＡＢ＝２０ｍ，ＡＣ＝１０ｍ，ＣＢ＝１０√３ｍの
三角形になり頂点ＣとＢとの間は１７．３２ｍになることが解ります。
このことから角（Ｃ、Ａ、Ｂ）は６０°
それが左右に有るので、すばらしい景色が見える範囲角度は１２０°
すばらしい景色１２０°÷ゴンドラ一周は３６０°＝１／３
　１４分×１／３＝４分４０秒

答え
４分４０秒

解答・その19

（ペンネ－ム：夜ふかしのつらいおじさん）

次の図のように「すばらしい景色」が見えるのは、１２０度の範囲なので１４分のうちの３分の１です。
だから、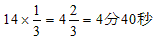です。

正解者

teki のっこん haya

BossF 転位反応杖のおじさん

T_Tatekawa 真夏のサンタ赤影

夜ふかしのつらいおじさんスモークマン迷子の雄猫

やなせバルタン星人巷の夢

オヤジ ykak 長崎島原　かがみ

三角定規

たくさんの方から、解答をお寄せいただき、どうもありがとうございました。
私の住む横浜にも、「コスモクロック」という大きな観覧車があります。今までは、遠くからイルミネーションを楽しむだけだったのですが、この機会に「すばらしい景色」を体験しなければということで、出かけてきました。最初の45°くらいは、だんだん高度があがっていくので、ちょっとどきどきでした。真下を見ないようにして景色を楽しんでいるうちに、頂点を過ぎ、徐々に下がりだすと、寂しいようなホットしたような・・・。
→　観覧車からのすばらしい景色

Challenge!