�P�S�W�D�K��̖��
���̐����ɑ��A���I�� ���̊K��Ƃ����A���ȉ��̑S�Ă̐��̐����̐ς�\�����̂Ƃ���B�Ⴆ�A
�@�@�@�S�I���S�~�R�~�Q�~�P���Q�S�ł���B
(1) �Q�O�I��f������������B
(2) �Q�O�I�̐��̖ŁA�������ł�����̂͂������邩�B���̌�����B
�����ɁA�������Ƃ́A�P�A�W�A�Q�V�Ȃǂ̂悤�ɁA���鐳�����̂R��ŕ\����鐔�̂��Ƃ������B
(3) �Q�O�I�̐��̖ŁA�P�X�I�̖łȂ����̂͂������邩�B
���̌���f�������������`�œ�����B
(4) �Q�O�I�̐��̖ŁA�i�P�O�i�@�ŕ\�����Ƃ��́j�e���̘a���Q�ł�����̂�
�������邩�B���̌�����B
���̏o�T
�L���t�n�C���x�����w���w�ɒ���
�Z���I�����s�b�N�ψ���ďC
�u�k�Ѓu���[�o�b�N�X
2006�N�t�@�C�i�����
�����Ɖ��
�E����1
�i�y���l�|���F�O�p��K�j
(1) 20!��218�E38�E54�E72�E11�E13�E17�E19
(2) 23��a�C33��b�C53=c �Ƃ����ƁC
�@20!��a6�Eb2�Ec�E11�E13�E17�E19�@�ł��邩��C
�@�������ł���̌��� (6�{1)3�{1)(1�{1)��42 ��
(3) Pass
(4) ��ӂ������̂́C
�@2�C 20�C 200�C 2000�C 20000�@�� 2�E(2�E5)n (n��0�C1�C2�C3�C4)
�@11�C 110�C 1100�C 11000�C 110000�@�� 11�E(2�E5)n
�@1001�C10010�C100100�C1001000�C10010000�@�� 7�E11�E13�E(2�E5)n
�@�� 15 �� ������������B���̑��ɂ́C
�@101 �� 3�C7 ��ɂ����Ȃ��B
�@10001 �́C3�C7�C11�C13�C17�C19 ��ɂ����Ȃ��B
�@100001��11�E9091 �ŁC9091 �� 3�C7�C11�C13�C17�C19 ��ɂ����Ȃ��B
�@1000001��969969��3�E7�E11�E13�E17�E19
�@������C�����܂Œ��ׂ�悭�C���̌��́C15 �B�@��
�E����2
�i�y���l�|���F���q�̗Y�L�j
(1)�Q�O�I���P�X���P�V���P�R���P�P���V�Q���T�S���R�W���Q�P�W
(2) �Q�O�I�̐��̖ŁA�������ł�����̂�
�i�T�O���T�R�j���i�R�O���R�R���R�U�j��
�i�Q�O���Q�R���Q�U���Q�X���Q�P�Q���Q�P�T���Q�P�W�j
�ł��邩����́A2*3*7��
(3) �P�X�I�͂P�X���P�V*�P�R*�P�P*�V�Q���T�R���R�W���Q�P�U
�ł��邩��A
�i�P�X�O���P�X�P�j��
�i�P�V�O���P�V�P�j��
�i�P�R�O���P�R�P�j��
�i�P�P�O���P�P�P�j��
�i�V�O���V�P���V�Q�j��
�i�R�O���R�P���R�Q���R�R���R�S���R�T���R�U���R�V���R�W�j��
�o
�@�@�i�T�S���Q�O�`�Q�P�U�j
�@�@�܂���
�@�@�i�T�O�`�T�S���Q�P�V�`�Q�P�W�j
�p
�ł��邩��
�@�Q�S���R���X���i�P�V�{�T���Q�j
���Q�S���R���X���Q�V
���Q�S���R���X���R���X
���Q�S���R�U�i�j
(4) �Q�O�I�̐��̖ŁA�i�P�O�i�@�ŕ\�����Ƃ��́j�e���̘a���Q�ł�����̂�
���Ƃ��Ĉȉ��̂��̂��l������B
�@�i���j2���i�P�O�O�`�P�O�S�j
�@�i���j11���i�P�O�O�`�P�O�S�j
�@�i���j101���i�P�O�O�`�P�O�S�j
�@�i���j1001���i�P�O�O�`�P�O�S�j
�@�i���j10001���i�P�O�O�`�P�O�S�j
�@�i���j100001���i�P�O�O�`�P�O�S�j
�@�i���j1000001���i�P�O�O�`�P�O�S�j
10..01�̌`�̐����́A2,3,5�Ŋ����Ȃ��͎̂����Ȃ̂ŁA
�P�X���P�V*�P�R*�P�P*�V�Q��2263261���10000001�i�O�͂U�j�ȏ�͖�
�Ȃ肦�Ȃ��B
�i�P�O�O�`�P�O�S�j�����́i�i�Q���T�j�O�`�i�Q���T�j�S�j�ł���̂łQ�O�I�̖�
����đO�������̂ݒ��ׂ�B�ȉ��i�P�j�̌��ʂ��E�E�E
�@�i���j�Q�͂Q�O�I�̖A�Ȃ̂łQ�O�I�̖�
�@�i���j�P�P�͂Q�O�I�̖A�Ȃ̂łQ�O�I�̖�
�@�i���j�P�O�P�͑f���A�Ȃ̂łQ�O�I�̖ł͂Ȃ�
�@�i���j�P�O�O�P���V���P�P���P�R�A�Ȃ̂łQ�O�I�̖�
�@�i���j�P�O�O�O�P�͂V�`�P�X�̂�����ł������Ȃ��̂łQ�O�I�̖ł͂Ȃ�
�@�i���j�P�O�O�O�O�P���P�P���X�O�X�P�ŁA�X�O�X�P��7,13,17,19�̂�����ł������Ȃ��̂łQ�O�I�̖ł͂Ȃ�
�@�i���j�P�O�O�O�O�O�P�͂V�`�P�X�̂�����ł������Ȃ��̂łQ�O�I�̖ł͂Ȃ�
����Ď��ۂɂQ�O�I�̐��̖ŁA�i�P�O�i�@�ŕ\�����Ƃ��́j�e���̘a���Q�ł�����̂�
�ȉ��̂R���T�i�j���P�T�i�j
�@�i���j2���i�P�O�O�`�P�O�S�j
�@�i���j11���i�P�O�O�`�P�O�S�j
�@�i���j1001���i�P�O�O�`�P�O�S�j
�E����3
�i�y���l�|���Fhaya�j
(1)���� �@218 * 38 * 54 * 72 * 11 * 13 * 17 * 19
(2)�����@42��
(3)�����@24 * 36
(4)�����@15��
�y�������z
(1) 1�`20�܂ł̐��������ꂼ��f�����������A�w������������
(2) 1=13 ��ʊi�Ƃ��āA23, 33, 53 ��g�ݍ��킹��
�@[1] 1��ނ�
�@�@13
�@�@23, 26, 29, 212, 215, 218
�@�@33, 36
�@�@53
�@[2] 2��ގg����
�@�@23*33, 23*36, 23*53,
�@�@26*33, 26*36, 26*53,
�@�@29*33, 29*36, 29*53
�@�@212*33, 212*36, 212*53,
�@�@215*33, 215*36, 215*53,
�@�@218*33, 218*36, 218*53
�@�@33*53, 36*53
�@[3] 3��ގg����
�@�@23*33*53, 23*36*53,
�@�@26*33*53, 26*36*53,
�@�@29*33*53, 29*36*53,
�@�@212*33*53, 212*36*53,
�@�@215*33*53, 215*36*53,
�@�@218*33*53, 218*36*53
�ȏ�A�v42��
(3) 217, 218, 54 �������19!�̖ɂȂ�Ȃ�
�@[1] 217 �܂��� 218 �������Ă��邪 54 �������Ă��Ȃ��P�[�X
�@�@2�̗ݏ��2��ށA3�̗ݏ��0�`8�܂ł�9��ށA5�̗ݏ��0�`3�܂ł�4��ށA
�@�@7��0�`2�܂ł�3��ށA11, 13, 17, 19 �͂��ꂼ�� 0�`1 �̃o���G�[�V���������邩��A
�@�@2*9*4*3*24
�@[2] 217 �y�� 218 �͓��炸 54 �������Ă���P�[�X
�@�@���l�ɁA17*9*1*3*24
�@[3] 217 �܂��� 218 �� 54 �������ɓ����Ă���P�[�X
�@�@2*9*1*3*24
���߂����
�@[1]+[2]+[3] = (2*4 + 17*1 + 2*1)*9*3*24 = 27*9*3*24 = 24 * 36
(4) 20 ! �̖́Aa=0�`18 , b=0�`8, c=0�`4, d=0�`2, e=0�`1, f=0�`1, g=0�`1, h=0�`1 �Ƃ��āA
�@2a * 3b * 5c * 7d * 11e * 13f * 17g * 19h
�Ə�����B���߂�̌����\�����鐔�l�� 2 ��1�ł���ȊO�� 0 �Ƃ����
�@2*10i
�̌`�ɏ�����B�@���������E�ӂƂ��鎮�����ΐ������A
�@a*log2 + b*log3 + c*log5 + d*log7 + e*log11 + f*log13 + g*log17 + h*log19 = log2 + i
b = d = e = f = g = h = 0 �͕K�R�ŁA
�@log2 + i*(log2 + log5) = log2 + i
�ƂȂ邩��Aj = 0, 1, 2, 3, 4 ��K�p���āA
�@2
�@20
�@200
�@2000
�@20000
�����\�����鐔�l�� 1 ��2�A����ȊO�� 0 �Ƃ����
�@2a * 3b * 5c * 7d * 11e * 13f * 17g * 19h = (10i + 1)*10j
���l�ɗ��ӂ̑ΐ�������
�@a*log2 + b*log3 + c*log5 + d*log7 + e*log11 + f*log13 + g*log17 + h*log19 = log(10i + 1) + j
i = 1 �� i = 3 �̎��ɂ��ꂼ��
�@log11 + j(log2 + log5) = log11 + j
(log 7 + log11 + log13) + j(log2 + log5) = log1001 + j
�ƂȂ邩��Aj = 0, 1, 2, 3, 4 ��K�p���āA
�@11
�@110
�@1100
�@11000
�@110000
�@��
�@1001
�@10010
�@100100
�@1001000
�@10010000
��B�@�]���āA���̌��� 15��
�E����4
�i�y���l�|���F�R�E�j
(1)���炩����20�I�Ɍ���鐮����f�����������w���̎c��`�ŕ\���ƁA
20��22*51�A19��191�A18��21*32�A17��171�A16��24�A15��31*51�A
14��21*71�A13��131�A12��22*31�A11��111�A10��21*51�A9��32�A
8��23�A7��71�A6��21*31�A5��51�A4��22�A3��31�A2��21
����������20�I��218*38*54*72*11*13*17*19�@ans.
(2) 20 �I �̐��̖��m�Ƃ����
�m��2a * 3b * 5c * 7d * 11e * 13f * 17g * 19h
�@�ƕ\����B
�i�A���Aa�`h�́A0��a��18�A0��b��8�A0��c��4�A0��d��2�A0��e��1�A0��f��1�A0��g��1�A0��h��1���������j
�m���������ƂȂ邽�߂ɂ́A�m�̑f�����̎w���܂�a�`h���A���ׂĂR�̔{���ƂȂ�悢�B
����ď�������a��7�ʂ�Ab��3�ʂ�Ac��2�ʂ�Ad�`h��1�ʂ�B
���������đ�ӂ����m�̌���7*3*2��42�� ans.
(3)
20�I��218*38*54*72*11*13*17*19
19�I��216*38*53*72*11*13*17*19
����������20�I�̐��̖̂����A217�A218�A54��
�Ɏ����̂�19�I�̐��̖Ɋ܂܂�Ȃ����ƂɂȂ�B
�@�j�m��217���܂܂��ꍇ
�@�@�f�����Q�ȊO�̎w���͔C�ӂɑI�ׂ�̂�
�@�@1*9*5*3*2*2*2*2��24*33*5��
�A�j�m��218���܂܂��ꍇ
�@�@�@�j�̏ꍇ�Ɠ��l�ɂ���1*9*5*3*2*2*2*2��24*33*5
�B�j�m��54���܂܂��ꍇ
�@�@�f�����T�ȊO�̎w���͔C�ӂɑI�ׂ�̂�
�@�@19*9*1*3*2*2*2*2��24*33*19
�C�j�m��54��217�A��������4��218���܂܂��ꍇ
�@�@�f�����Q�ƂT�ȊO�̎w���͔C�ӂɂɑI�ׂ�̂�
�@�@2*9*1*3*2*2*2*2��24*33*2
�ȏ��苁�߂����24*33*(5+5+19-2)��24*36�� ans.
(4)
��ӂ�������
[1] 2*10n
[2] �l*10n�@�̂ǂ��炩�̌`�ŕ\�����B
�i�A���l��m���̐���1�ʂ̐���m�ʂ̐���1�j
[1] �̏ꍇ
�@�@n��20�I��2��5�̎w���̊W���0��n��4�ƂȂ�̂ŋ��߂����5�B
[2] �̏ꍇ
�@�@�܂��l�ɂ��čl����B
�@�@M�͊i���̘a���Q�ł��邱�ƂƁA�P�ʂ̐����P�ł��邱�Ƃ��A���Ȃ��Ƃ��Q�C�R�C�T�̔{���ł͂Ȃ��B
�@�@����Ăl��72*11*13*17*19��2263261
�@�@���������Ăl��1000001�C100001�C10001�C1001�C101�C11
�@�@���̂���20�I�̖ł���̂�1001�i��7*11*13�j��11�̂�
�@�@���[1]�Ɠ��l�ɂ���2*5��10�B
�ȏ��苁�߂����15�� ans.
�E����5
�i�y���l�|���FK�̐l�j
(1)
�K��̒�`���
�@20 ! =1�~2�~3�~4�~...�~19�~20�@�ł��̂ŁA���ꂼ��̈�����f������������Γ����������܂��B
�@4=22 , 6=3�~2 , 8=23 , 9=32 , 10=5�~2 , 12=22�~3 , 14=7�~2 ,
�@15=3�~5 , 16=24 , 18=32�~2 , 20��5�~22 (�f���͏ȗ�)
����ē����́A
�@20 ! =218�~38�~54�~72�~11�~13�~17�~19
(2)
(1)�̓����𗘗p���܂��B
���ׂĂ̎��R���͑f���̐ςŕ\�����Ƃ��ł��A���������̑g�ݍ��킹��1�ʂ肵������܂���B
�������̌������߂�ȏ�A�g�p����f���͏��Ȃ��Ƃ��������̂�3�Ȃ��Ă͂����܂���B
�@����� 2 , 3 , 5
���炢�����̐���I��Ŋ|�����킹�����̂ɂȂ�܂����A2����͍ő�6�A3����͍ő�2�A
5����͍ő�1�̐������g�����Ƃ��o���܂���B
�Ȃ̂�2�����0�`6��7�ʂ�A3�����0�`2��3�ʂ�A
5�����0�`1��2�ʂ�̑I�ѕ������邱�ƂɂȂ�̂œ�����
�@ 7�~3�~2=42
�ƂȂ���42�̑g�ݍ��킹�������邱�ƂɂȂ�A���ꂪ�����ƂȂ�܂��B
�@A, 42��
(3)
(1)�̓����𗘗p���܂��B
�@20 ! =218�~38�~54�~72�~11�~13�~17�~19
�ł����̂� 19! �͂���� 20=22�~5 �Ŋ��������ɂȂ�܂��B���Ȃ킿
�@19 ! =216�~38�~53�~72�~11�~13�~17�~19
�͂��ꂼ��̑f�����炢������I�т������킹�����̂ɂȂ�܂��̂�(2)�Ɠ����v�̂�
20 ! �̖̌���
�@19�~9�~5�~3�~2�~2�~2�~2 (��)
19 ! �̖̌���
�@17�~9�~4�~3�~2�~2�~2�~2 (��)
������
(19�~9�~5�~3�~2�~2�~2�~2)-(17�~9�~4�~3�~2�~2�~2�~2)=24�~33�~((19�~5)-(17�~4))
=24�~33�~27=24�~36
�@ A.24�~36 ��
(4)
���̏ꍇ�e���̐���2�Ƃ�������0�ō\������Ă���ꍇ�ƁA2��1�Ƃ�������0�ō\������Ă���ꍇ���l�����܂��B
2�Ƃ�������0�ō\������Ă���ꍇ�K��2���ŏ��ɕt���A���̂��Ƃ�0�������������Ƃ����`�ɂȂ�܂��B
�����f������������ƁA
�@2�~(2�~5)n
�ƕ\�����Ƃ��o���܂��B����Ă��̏ꍇ�̌���20 ! �̑f������5�̑I�ѕ��A���Ȃ킿5�ʂ�ƂȂ�܂��B
2��1�Ƃ�������0�ō\������Ă���ꍇ���̂悤�ɑf������������܂��̂ŁA
�@11�~(2�~5)n
���̏ꍇ��5���݂��邱�ƂɂȂ�܂��B
����ɁA1���ŏ��ɂ��ĊԂ�0������������Ō��1�����Ƃ������̂ōl���Ă݂����ʁA
�����ɓ��Ă͂܂���̂Ƃ��āA1001������܂��B
�@1001�~(2�~5)n
���̏ꍇ��5���݂��܂��B
3�̐������v���ē�����15��
�E����6
�i�y���l�|���F�]�ʔ����j
(1) �Q�O�I���Q�O�~�P�X�~�P�W�~�P�V�~�P�U�~�P�T�~�P�S�~�P�R�~�P�Q�~�P�P�~�P�O�~�X�~�W�~�V�~�U�~�T�~�S�~�R�~�Q�~�P
�����ŁA
�@�Q�O���Q�~�Q�~�T
�@�P�W���Q�~�R�~�R
�@�P�U���Q�~�Q�~�Q�~�Q
�@�P�T���R�~�T
�@�P�S���Q�~�V
�@�P�Q���Q�~�Q�~�R
�@�P�O���Q�~�T
�@�@�X���R�~�R
�@�@�W���Q�~�Q�~�Q
�@�@�U���Q�~�R
�@�@�S���Q�~�Q
����āA
�Q�O�I���Q18�~�R8�~�T4�~�V2�~�P�P�~�P�R�~�P�V�~�P�X
(2)�f���̗������́A�P�C�Q�R�C�R�R�C�T�R �E�E�E(1)
�����ŁA
�Q18���S�X���W�U���P�U�S.�T���R�Q�R.�U���U�S�R����A�S�R�C�W�R�C�P�U�R�C�R�Q�R�C�U�S�R���ŗ������E�E�E(2)
�R�W���X�S����A�X�R���ŗ������E�E�E(3)
�����̗��������g�����Ăł���͂Q�O�E�E�E(4)
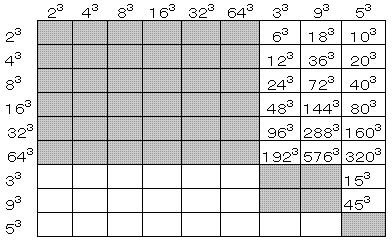
����ɁA�O�g�����Ăł���͂P�Q�E�E�E(5)
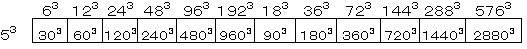
����āA(1)�`(5)�����v���ĂS�Q��
(3) �Q�O�I���Q18�~�R8�~�T4�~�V2�~�P�P�~�P�R�~�P�V�~�P�X
�@�@�@�@�@�@���Q�O�~�P�X�I
�@�@�@�@�@�@���Q2�~�T�~�P�X�I
����āA
�P�X�I��16�~�R8�~�T3�~�V2�~�P�P�~�P�R�~�P�V�~�P�X
��ӂ̌��́A�Q�O�I�̖ƂP�X�I�̖̌��̍��ł��邩��A
�@���P�X�~�X�~�T�~�R�~�Q�~�Q�~�Q�~�Q�|�P�V�~�X�~�S�~�R�~�Q�~�Q�~�Q�~�Q
�@���i�P�X�~�T�|�P�V�~�S�j�~�X�~�R�~�Q�~�Q�~�Q�~�Q
�@���Q�V�~�X�~�R�~�Q�~�Q�~�Q�~�Q
�@���Q�S�~�R�U
(4)�e���̘a���Q�ł��鐮���́A�P���Q�܂ށA�����͂Q���ЂƂ܂݁A�c��̌��͂O�ł���B
��̓I�ɂ́A�Q�A�P�P�A�y�ш�ʂƍŏ�ʂ��P�ŁA���̈ʂ͑S�ĂO�ł��鐮���i�Ⴆ�P�O�O�P�j��
�����̂P�O�{�A�P�O�O�{�A�P�O�O�O�{�A�P�O�O�O�O�{�̐����ł���B
�����ŁA�P�O�O�P���V�~�P�P�~�P�R�Ȃ̂ŁA�P�O�O�P�́A�Q�O�I�̖ł���B
���̃^�C�v�̐����ŁA�Q�O�I�̖ƂȂ���̂́A���ɂ͖����B
���͈ȉ��̒ʂ�B
�P�O�O�E�E�E�O�O�P�̃^�C�v�̐����́A���炩�ɂQ�A�R�A�T��Ɏ����Ȃ��B
����ŁA
�V2�A�P�P�A�P�R�A�P�V�A�P�X�̖̑g�����ŁA��ʂ��P�ƂȂ�g�����́A
�ȉ��̒ʂ�ł��邪�A��ӂ��������͂P�O�O�P�̂݁B
�@�R�~�P�V���X�P
�@�R�~�P�V�~�P�P���P�O�O�P
�@�P�R�~�P�V���Q�Q�P
�@�P�R�~�P�V�~�P�P���Q�S�R�P
�@�V�~�V�~�P�X���X�R�P
�@�V�~�V�~�P�X�~�P�P���P�O�Q�S�P
�@�V�~�V�~�P�R�~�P�V�~�P�X���Q�O�T�V�T�P
�@�V�~�V�~�P�P�~�P�R�~�P�V�~�P�X���Q�Q�U�R�Q�U�P
����āA��ӂ��������́A�ȉ��̂P�T�ʂ�B
�P�P���P�P�~�P
�P�P�O���Q�~�T�~�P�P
�P�P�O�O���Q�~�T�~�Q�~�T�~�P�P���Q�Q�~�T�Q�~�P�P
�P�P�O�O�O���Q�Q�~�T�Q�~�Q�~�T�~�P�P���Q�R�~�T�R�~�P�P
�P�P�O�O�O�O���Q�R�~�T�R�~�Q�~�T�~�P�P���Q�S�~�T�S�~�P�P
�P�O�O�P���V�~�P�P�~�P�R
�P�O�O�P�O���Q�~�T�~�V�~�P�P�~�P�R
�P�O�O�P�O�O���Q�~�T�~�Q�~�T�~�V�~�P�P�~�P�R���Q�Q�~�T�Q�~�V�~�P�P�~�P�R
�P�O�O�P�O�O�O���Q�~�T�~�Q�Q�~�T�Q�~�V�~�P�P�~�P�R���Q�R�~�T�R�~�V�~�P�P�~�P�R
�P�O�O�P�O�O�O�O���Q�~�T�~�Q�R�~�T�R�~�V�~�P�P�~�P�R���Q�S�~�T�S�~�V�~�P�P�~�P�R
�Q���Q�~�P
�Q�O���Q�~�Q�~�T���Q�Q�~�T
�Q�O�O���Q�Q�~�T�~�Q�~�T���Q�R�~�T�Q
�Q�O�O�O���Q�R�~�T�Q�~�Q�~�T���Q�S�~�T�R
�Q�O�O�O�O���Q�S�~�T�R�~�Q�~�T���Q�T�~�T�S
�E����7
�i�y���l�|���F�J�̖��j
�i1�j
20�I��20�~19�~18�~�E�E�E�E�E�E�E�E�E�E�~3�~2�~1
�@�@��218�~38�~54�~72�~11�~13�~17�~19
�i2�j
��L�i1�j���
| �E2�݂̂Ō`������� | �F | 23,(22)3,(23)3,(24)3,(25)3,(26)3 |
| �E3�݂̂Ō`������� | �F | 33,(32)3 |
| �E5�݂̂Ō`������� | �F | 53 |
| �E2��3�Ō`������� | �F | (2�~3)3,(22�~3)3,(23�~3)3,(24�~3)3,(25�~3)3,(26�~3)3 (2�~32)3,(22�~32)3,(23�~32)3,(24�~32)3,(25�~32)3,(26�~32)3 |
| �E2��5�Ō`������� | �F | (2�~5)3,(22�~5)3,(23�~5)3,(24�~5)3,(25�~5)3,(26�~5)3 |
| �E3��5�Ō`������� | �F | (3�~5)3,(32�~5)3 |
| �E2��3��5�Ō`������� | �F | (2�~3�~5)3,(22�~3�~5)3,(23�~3�~5)3,(24�~3�~5)3,(25�~3�~5)3,(26�~3�~5)3 (2�~32�~5)3,(22�~32�~5)3,(23�~32�~5)3,(24�~32�~5)3,(25�~32�~5)3,(26�~32�~5)3 |
| �E1�Ō`������� | �F | 13 |
�����A42�ƂȂ�B
�i3�j
19�I��19�~18�~�E�E�E�E�E�E�E�E�E�E�~3�~2�~1
�@�@��216�~38�~53�~72�~11�~13�~17�~19
20�I��20�~19�~18�~�E�E�E�E�E�E�E�E�E�E�~3�~2�~1
�@�@��20�~19!
19�I�̖̌��i16+1�j�E�i8+1�j�E�i3+1�j�E�i2+1�j�E2�E2�E2�E2�@�� 26�~33�~17
20�I��218�~38�~54�~72�~11�~13�~17�~19
20�I�̖� 24�~33�~5�~19
�����āA�����̍����@ 24�~33�~5�~19-26�~33�~17
���@24�~36�����߂���̂ł���B
�i4�j
��ӂ��2�Ƃ���10�̗ݏ�{�̂��́A11�Ƃ���10�̗ݏ�{�̂��́A101,1001,10001�A�E�E�E�E�E
�����Ƃ��čl������B
10��2�~5�ł��邩��A2�A2�~�i2�~5�j�A2�~�i2�~5�j2�A2�~�i2�~5�j3�A2�~�i2�~5�j4
�S�����l��11�A11�~�i2�~5�j�A11�~�i2�~5�j2�A11�~�i2�~5�j3�A11�~�i2�~5�j4
1001��7�~11�~13�ł��邩��A��L�Ɠ��l��
7�~11�~13�A7�~11�~13�~�i2�~5�j�A7�~11�~13�~�i2�~5�j2�A7�~11�~13�~�i2�~5�j3�A
7�~11�~13�~�i2�~5�j4
�����A15�ł���B
�E����8
�i�y���l�|���FBossF�j
*�@�\�̈ꕔ���C�����܂�(5/6)�B�����܂���BJunko
(1)���̂悤�ȕ\���v�������ׂ܂���
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 |
|---|---|---|---|---|---|---|---|
| 10 | 6 | 4 | 2 | 1 | 1 | 1 | 1 |
| 5 | 2 | 1 | �@ | �@ | �@ | �@ | �@ |
| 2 | �@ | �@ | �@ | �@ | �@ | �@ | �@ |
| 1 | �@ | �@ | �@ | �@ | �@ | �@ | �@ |
| 18 | 8 | 5 | 2 | 1 | 1 | 1 | 1 |
20!=218�E38�E54�E72�E11�E13�E17�E19�@��
(2)(1)��藧�����̈����ɂȂ肤��̂�
2,3,5�A�ł��̌��͊e�X6��2��1�܂�
�@��(6+1)(2+1)(1+1)=42�@��
(3)20=22x5 ������@19!= 216�E38�E53�E72�E11�E13�E17�E19
����������
20�̖̌�-19�̖̌�=(19x5-17x4)x9x3x24=36x24�@��
(4)�e���̘a��2��20!�̖ň�̈ʂ�0�łȂ����̂�
2,11,1001�̂�
�e�X��1,10,100,1000���悶�����̂����߂���̂ł��邩��
3��5��15�@��
�E����9
�i�y���l�|���F�r�n�t�j
(1)
�@�@218�E38�E54�E72�E11�E13�E17�E19�@��
(2)
�@�@�������ɂȂ�\�����������́A2,3,5 �݂̂ŁA
( 1 + 23 + 26 + �c + 218 )(1 + 33 + 36)(1 + 53)
��W�J���đS�Ă̗������������܂��B
�@�@�W�J��̍����� 7*3*2=42 �ƂȂ�A���ꂪ�����@��
(3)
�@�@n�̖̏W����Sn�ƒ�`���܂��B
�@�@�܂��A20!�̖̏o�������l����ƁA
�@�@�@20! = 20*19!
�@�@����A
�@�@�@S20! = { s*t | s��S20 , t��S19! }
�@�@�Ƃ����`�ɂȂ��Ă��邱�Ƃ��킩��܂�����A
�@�@�@S20! �� S19!�@�@�c��
���]���܂��B
�@�@�܂��A(2)�̂悤�ȍl�����ɂ��A
�@�@�@n(S20!) = 24�33�5�19
�@�@�@n(S19!) = 26�33�17�@�c����
�@�@�Ƃ킩��܂��B
�@�@�� �� ���� ����A�P���Ɉ����Z�ōςނ��Ƃ��킩���Ă���̂ŁA
�@�@n(S20!) - n(S19!) = 24�36�@�������B�@��
(4)
�@�@�p�^�[���Ƃ��ẮA
�@�@�@[1]2��1�Ƃ�������0�ō\����������
�@�@�@[2]1��2�Ƃ�������0�ō\����������
�@�@��2�ʂ�B
�@�@[1]�Ɋւ��ẮA5��4�����������߁A
�@�@�@2 , 20 , 200 , 2000 , 20000
�@�@�@��5�ʂ肵�����݂��܂���B
�@�@[2]�ɂ��āA�����2�ʂ�ɕ������A
�@�@�@�@i) 10�c01 �̂悤��1�ŏI����Ă������(2��5���܂܂Ȃ�)
�@�@�@�@ii)10�c010�c0 �̂悤�ɓr����1������A0�ŏI����Ă������
�@�@�@�̂悤�ɂȂ�܂��B
�@�@�@ii) �ɂ��ẮA�����ł���2��5���Ă��܂��� i) �ɋA���ł���̂ŁA
�@�@�@i) �������l���܂��B
�@�@�@
�@�@�@�܂��A
�@�@�@�@11��S20!�@�@�@�@�@
�@�@�@�@1001=7�11�13��S20! �����
�@�@�@���]���܂��B
�@�@�@����������ȊO�̂��̌`�̐��ɂ��ẮA
�@�@�@�@101:�f��
�@�@�@�@10001=73�137
�@�@�@�@100001=11�9091
�@�@�@�@1000001=101�9901
�@ 10000001=11�909091
�@�@�@�@100000001=17�5882353
�@�@�@�@1000000001=7�11�13�19�52579
�@�@�@�@10000000001=101�3541�27961
�@�@�@�ƂȂ�A�S�� S20! �Ɋ܂܂�܂���B
�@�@�@(�������2��5���������ő�̐���2121322203�Ȃ̂ŁA�����܂łŏ\��)
�@�@�@������ S20! �̌��ɂ��\�����Ƃ��o���Ȃ����߁A
�@�@�@���LJA�̌`�ɂ��āA������
�@�@�@�@11 , 110 , 1100 , 11000 , 110000
�@�@�@�@1001 , 10010 , 100100 , 1001000 , 10010000
�@�@�@��10�ʂ肵���Ȃ����ƂɂȂ�܂��B
�@�@�ȏ�̂��Ƃ���A������15�� ��
�E����10
�i�y���l�|���F�I���W�j
(1)�P�`�Q�O�܂ł̑f���́A�o�Q�C�R�C�T�C�V�C�P�P�C�P�R�C�P�V�C�P�X�p
[�@]���AGauss�L���Ƃ���B
�Q�O�I���Q���~�R���~�T���~�V���~�P�P�~�P�R�~�P�V�~�P�X
�i�f���������j�Ƃ����
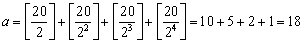
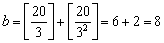
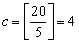
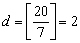
�]����
���@�Q�O�I���Q�P�W�~�R�W�~�T�S�~�V�Q�~�P�P�~�P�R�~�P�V�~�P�X
(2)�������́A���L�̂R�̏W������P���I���̐ςł���B
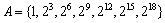
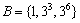
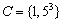
�]���ā@���߂闧�����̌��́@�V�~�R�~�Q���S�Q�@�@�@���@�S�Q��
(3) (1)���@�Q�O�I���Q�P�W�~�R�W�~�T�S�~�V�Q�~�P�P�~�P�R�~�P�V�~�P�X
���l�Ɂ@�@ �P�X�I���Q�P�U�~�R�W�~�T�R�~�V�Q�~�P�P�~�P�R�~�P�V�~�P�X
���߂���́A�i�P�X�~�T�|�P�V�~�S�j�~�X�~�R�~�Q�~�Q�~�Q�~�Q���@�R�U�~�Q�S
�@�@�@���@�R�U�~�Q�S�@��
(4)�d��Ōv�Z���܂������R��Ă��Ȃ����S�z�ł��B
�Q�O�I�͉��S���@�O���S���ԁ@���̂Ȃ�@�P�O���Q�~�T�@�Ɓi�P�j���
�e���̘a���@�Q�ƂȂ�@���̍ŏ���Ƃ��ā@�R��ނ̂�
�o�Q�C�P�P�C�P�O�O�P�p�@�������@�P�O�O�P���V�~�P�P�~�P�R�@�]����
���߂鐔�́A�o�Q�C�Q�O�C�Q�O�O�C�Q�O�O�O�C�Q�O�O�O�O�C�P�P�C�P�P�O�C�P�P�O�O�C
�P�P�O�O�O�C�P�P�O�O�O�O�C�P�O�O�P�C�P�O�O�P�O�C�P�O�O�P�O�O�C�P�O�O�P�O�O�O�C
�P�O�O�P�O�O�O�O�p�́@�P�T�@�@�@�@�@�@�@�@�@�@�@�@���@�P�T��
�E����11
�i�y���l�|���F�̂�����j
�i�P�j�@�Q�O�I���Q�P�W�E�R�W�E�T�S�E�V�Q�E�P�P�E�P�R�E�P�V�E�P�X
�i�Q�j
�i�P�j�ɂ����ĂQ�̎w���͂P�W�A�P�W�ȉ��̂R�̔{����0�C�R�C�U�C�X�C�P�Q�C�P�T�C�P�W�̂V��
�i�P�j�ɂ����ĂR�̎w���͂W�A�W�ȉ��̂R�̔{���͂O�C�R�C�U��3��
�i�P�j�ɂ����ĂT�̎w���͂S�A�S�ȉ��̂R�̔{���͂O�C�R��2��
�@�������̌��́@�V�E�R�E�Q���S�Q�i�j
�i�R�j
�Q�O���Q�Q�E�T ������@�P�X�I���Q�P�U�E�R�W�E�T�R�E�V�Q�E�P�P�E�P�R�E�P�V�E�P�X
�Q�O�I�̖̌��́@�P�X�E�X�E�T�E�R�E�Q�E�Q�E�Q�E�Q
�P�X�I�́@�@�@�V�@�@�@�@�@�P�V�E�X�E�S�E�R�E�Q�E�Q�E�Q�E�Q
���߂����
�@�@�Q�S�E�R�R�E�T�E�P�X�|�Q�U�E�R�R�E�P�V
�@���Q�S�E�R�R�i�T�E�P�X�|�Q�Q�E�P�V�j
�@���Q�S�E�R�R�E�Q�V
�@���Q�S�E�R�U
�i�S�j
[1]�P���Q�i���͂O�j�̎�
�V�Q�E�P�P�E�P�R�E�P�V�E�P�X�ɂ��čl����
���̖͎��̂S�W��
�P�j�����P�ƂȂ�E�E�E�P�C11�C91,221,931�C1001�C2261�C2431�C10241�C24871�C205751�C2263261
�Q�j�����R�ƂȂ�E�E�E13,133,143,323,833�C1463�C3553�C9163�C12103�C29393�C133133�C323323
�R�j�����V�ƂȂ�E�E�E7�C17�C77,187,247,637�C1547�C2717�C7007�C15827�C17017�C174097
�S�j�����X�ƂȂ�E�E�E19�C49,119,209,539�C1309�C1729�C4199�C10829�C19019�C46189�C119119
���̂����A�P�P�ƂP�O�O�P�͑�ӂ���
�i�P�j�ɂ����ĂT�̎w���͂S����������
�P�P�̑��ɂP�P�O�C�P�P�O�O�C�P�P�O�O�O�C�P�P�O�O�O�O����ӂ����E�E�E�E�E���P
�P�O�O�P�̑��ɂP�O�O�P�O�C�P�O�O�P�O�O�C�P�O�O�P�O�O�O�C�P�O�O�P�O�O�O�O����ӂ����E�E�E�E���Q
�P�j�̖��W�P�{���Ă��P���Q�i���͂O�j�ɂȂ邱�Ƃ͂Ȃ�
�@�@�@�V�@�@�U�T�U�P�{�@�@�@�@�@�@�@�@�@�@�V
�Q�j�̖��Q�V�{�@�@�@�@�@�@�@�@�@�@�@�V
�@�@�@�V�@�@�Q�P�W�V�{�@�@�@�@�@�@�@�@�@�@�V
�R�j�̖��R�{�@�@�@�@�@�@�@�@�@�@�@�@�V
�@�@�@�V�@�@�Q�S�R�{�@�@�@�@�@�@�@�@�@�@�@�V
�S�j�̖��X�{�@�@�@�@�@�@�@�@�@�@�@�@�V
�@�@�@�V�@�V�Q�X�{�@�@�@�@�@�@�@�@�@�@�@�@�V
[2]�Q���P�i���͂O�j�̎�
���炩�ɁA�Q�C�Q�O�C�Q�O�O�C�Q�O�O�O�C�Q�O�O�O�O�̂T����ӂ����E�E�E�E���R
���P�A���Q�A���R���@���߂���͂P�T�i�j
�E����12
�i�y���l�|���F�o���^�����l�j
(1) �Q18�~�R8�~�T4�~�V2�~�P�P�~�P�R�~�P�V�~�P�X
(2) �S�Q
(3) �Q4�~�R6
(4) �P�T��
�l�����F
�i�P�j�n���ɐ����܂����B�Q�ˋ����P�O�{�T�i�S�̔{���j�{�Q�i�W�̔{���j�{�P�i�P�U�j
�i�Q�j�R������̂͂Q�C�R�C�T�Ŋe�V�ʂ�A�R�ʂ�A�Q�ʂ�i�O��܂ށj�\�Ȃ̂ł��̐ςV�~�R�~�Q���S�Q
�i�R�j�̑�����ς̌`�ŋ��߂��̍����l����B
�@�Q�O�I�̖̌����P�X�~�X�~�T�~�R�~�Q�~�Q�~�Q�~�Q
�@�P�X�I�̖̌����P�V�~�X�~�S�~�R�~�Q�~�Q�~�Q�~�Q
�@�����Z���āA�i�X�T�|�U�W�j�~�Q4�~�R3���Q4�~�R6
�i�S�j�Q�ɂȂ�̂͂Q���P�܂��͂P���Q��
�@�Q�~�P�On�ƍl�����Ƃ��T�͂S��܂łȂ̂ŁA�T��
�@�P�P�~�P�On���������T��
�@�a���Q�Ȃ̂łR�͑f�����Ɋ܂܂�Ȃ��B
�@�����łV�C�P�P�C�P�R�C�P�V�C�P�X�̑g�����łQ�ɂȂ�\�����l����B
�@�V�~�P�R�~�P�P���P�O�O�P������������T�ł���B
�E����13
�i�y���l�|���Fteki�j
�P�D�Q�P�W�~�R�W�~�T�S�~�V�Q�~�P�P�~�P�R�~�P�V�~�P�X
�P�`�Q�O�܂łɂQ�̔{���́A�P�O�A�S�̔{���͂T�A�W�̔{���͂Q�A�P�U�̔{���͂P����܂��B
����ĂQ�͂P�O�{�T�{�Q�{�P���P�W�B
���l�ɂR�͂W�A�T�͂S�A�V�͂Q�A�P�P�C�P�R�C�P�V�C�P�X�͊e�P�B
�Q�D�S�Q��
��ʓI�Ɂ@�m��ap*bq*cr�E�E�E�E�E�E�E�E�@�@�Ƃ���ƁA
�m�̖̌��i�P�y�т��̐����g���܂ށj�́A(p+1)*(q+1)*(r+1)�E�E�E�E
�ł��邱�Ƃ𗘗p���܂��B
�������͂��R�̌`�ɂȂ�̂ŁA���ꂪ�\�Ȉ����͂Q�C�R�C�T�̂R�ł��B
�Q�́A�Q�R�A�Q�U�A�Q�X�A�Q�P�Q�A�Q�P�T�A�Q�P�W�̂U��ށA
�R�́A�R�R�A�R�U
�̂Q��ށA�T�͂T�R�̂P��ނł��̂ŁA
�i�U�{�P�j�~�i�Q�{�P�j�~�i�P�{�P�j���S�Q �ł��B
�R�D�R�U�~�Q�S
�Q�Ɠ��l�ɖ̌��̒藝���g���܂��B
�Q�O�I�̖̌��́A
�@�i�P�W�{�P�j�~�i�W�{�P�j�~�i�S�{1�j�~�i�Q�{�P�j�~�Q�~�Q�~�Q�~�Q��
����A�P�X�I�̖̌��́A
�@�i�P�U�{�P�j�~�i�W�{�P�j�~�i�R�{1�j�~�i�Q�{�P�j�~�Q�~�Q�~�Q�~�Q��
�Q�O�I�̖͕K���P�X�I�̖Ȃ̂ŁA���̂Q�̍�����ӂ̌��ł��B
�@�X�~�R�~�P�U�~�i�P�X�~�T�|�P�V�~�S�j���R�R�~�Q�S�~�Q�V���R�U�~�Q�S
�S�D�Q�A�Q�O�A�Q�O�O�A�Q�O�O�O�A�Q�O�O�O�O�A�P�P�A�P�P�O�A�P�P�O�O�A�P�P�O�O�O�A�P�P�O�O�O�O
�P�O�O�P�A�P�O�O�P�O�A�P�O�O�P�O�O�A�P�O�O�P�O�O�O�A�P�O�O�P�O�O�O�O�@�̌v�P�T��
���ł��B
�܂��A�e���̘a���Q�ł��鐔�́A�R�̔{���ł͂��蓾�܂���B
�܂��A�P�O�̔{���łȂ��T�̔{���ł����蓾�܂���B
[1]�@�Q�E�E�E�E�E�@�̃p�^�[���i�E�E�E�E�E�͂O�̘A���j
�Q�O�I�ɂ́A�����T���S����̂ŁA�O�̘A���͍ő�S�B
[2]�@�P�E�E�E�P�E�E�E�@�̃p�^�[���i�E�E�E�͂O�̘A���j
�㔼�̂O�̘A���́A[1]�ł��q�ׂ��Ƃ���A�ő�łS�ł��B
���́A�P�ƂP�̊Ԃ̂O�̘A�����ł����A
�@�V�Q�~�P�P�~�P�R�~�P�V�~�P�X�@���Q�Q�U�R�Q�U�P
�Ȃ̂ŁA�O����U�܂Œ��ׂ�Ώ\���ł��B
�P�P�A�P�O�P�A�P�O�O�P�A�P�O�O�O�P�A�P�O�O�O�O�P�A�P�O�O�O�O�O�P�A�P�O�O�O�O�O�O�P��
�����A�V�A�P�P�A�P�R�A�P�V�A�P�X�̈����݂̂����̂́A�P�P�y�тP�O�O�P
�i���V�~�P�P�~�P�R�j�̂Q�݂̂ł��B
�i�P�O�O�O�O�P���P�P�~�X�O�X�P�B�P�O�O�O�O�O�O�P���P�P�~�X�O�X�O�X�P�ł����A
��������V�A�P�P�A�P�R�A�P�V�A�P�X�Ŋ����܂���B�j
�E����14
�i�y���l�|���FT_Tatekawa�j
(1)
1�`20 �őf���� 2, 3, 5, 7, 11, 13, 17, 19
�@�@2�Ŋ����鍇������ 9�D
�@�@22=4 �Ŋ����鍇������ 5�D
�@�@23=8 �Ŋ����鍇������ 2�D
�@�@24=16 �Ŋ����鍇������ 1�D
�@�@3�Ŋ����鍇������ 5�D
�@�@32=9 �Ŋ����鍇������ 2�D
�@�@5�Ŋ����鍇������ 3�D
�@�@7�Ŋ����鍇������ 1�D
�ȏォ��C
�@�@20 ! = 2(1+9+5+2+1) x 3(1+5+2) x 54 x 72 x 11 x 13 x 17 x 19
�@�@�@�@ = 218 x 38 x 54 x 72 x 11 x 13 x 17 x 19
(2)
�������ł�������ɂ́C23, ..., 218, 33, 36, 53 �̂����ꂩ���܂ލ����������悢�D
�@�@ (1+6) x (1+2) x (1+1) = 42 �ʂ�
(3)
20 = 22 x 5
�Ȃ̂ŁC20! �̐��̖ŁC19! �̖łȂ����̂̐��́C
�@�@�@19 x 9 x 5 x 3 x 24 - 17 x 9 x 4 x 3 x 24
�@�@=(95-68) x 33 x 24
�@�@= 27 x 33 x 24
�@�@= 24 x 36 ��
(4)
�@2, 20, 200, 2000, 20000
�@11, 110, 1100, 11000, 110000
�@1001 =(7x11x13), 10010, 100100, 1001000, 10010000
���v15��
�E����15
�i�y���l�|���Fkiyo�j
1)
�@�@20 ! =218*38*54*72*11*13*17*19
2)
�@�@20 ! =(23)6*(33)2*32*(53)*5*72*11*13*17*19
�@�@(6+1)*(2+1)*(1+1)=42
3)
�@�@�@(18+1)*(8+1)*(4+1)*(2+1)*(1+1)*(1+1)*(1+1)*(1+1)-(16+1)*(8+1)*(3+1)*(2+1)*(1+1)*(1+1)*(1+1)*(1+1)
�@�@=(8+1)*(2+1)*(1+1)*(1+1)*(1+1)*(1+1)((18+1)*(4+1)-(16+1)*(3+1))
�@�@=32*3*24*(19*5-17*4)
�@�@=24*33*(95-68)
�@�@=24*33*27
�@�@=24*33*33
�@�@=24*36
4)
�@�@15�B
2=2
11=11
20=22*5
110=2*5*11
200=23*52
1001=7*11*13
1100=22*52*11
2000=24*53
10010=2*5*7*11*13
11000=23*53*11
20000=25*54
100100=22*52*7*11*13
110000=24*54*11
1001000=23*53*7*11*13
10010000=24*54*7*11*13
�E����16
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
�i�P�j�Q�O�I���Q�P�W���R�W���T�S���V�Q���P�P���P�R���P�V���P�X�E�E�E[1]
�ƂȂ�܂��B
�i�Q�j�Q�R�C�R�R�C�T�R�̃u���b�N�Ɋ܂߂��ς̎������B
�Q�O�I���i�Q�R�j�U���i�R�R�j�Q���T�R���i�R�Q���T���V���P�P���P�R���P�V���P�X�j
����������
�i�U�{�P�j���i�Q�{�P�j���i�P�{�P�j���S�Q��
�i�R�j�Q�O�I�̐��̖̐���
�i�P�W�{�P�j�i�W�{�P�j�i�S�{�P�j�i�Q�{�P�j�i�P�{�P�j�i�P�{�P�j�i�P�{�P�j�i�P�{�P�j
���P�X���X���T���R���Q�S
���P�X���R�R���T���Q�S�E�E�E[2]
�P�X�I�̊K���
�P�X�I���Q�P�U���R�W���T�R���V�Q���P�P���P�R���P�V���P�X���Q���Q�E�E�E[3]
�P�X�I�̐��̖́i�P�U�{�P�j�i�W�{�P�j�i�R�{�P�j�i�Q�{�S�j�{�Q�S���Q�`�U���R���R���P�V�ł��B
�]���āA
���̍�[2]�\[3]���Q�S���R���R���T���P�X�|�Q�U���R�R���P�V
���Q�S���R�R���i�X�T�|�U�W�j���Q�S���R�R���Q�V���Q�S���R�U�ł��B
�i�S�j
�P���Q���A�Q����̂��̂�T���܂����B
���v���Q�ɂȂ�͎̂��̂T���l�����܂��B
�Q�ƂP�P�C�P�O�P�C�P�O�O�P�C�P�O�O�O�P�C�P�O�O�O�O�P�̂T�ł������̒���
�P�O�P�A�P�O�O�O�P�A�P�O�O�O�O�P�̂R�͂V�Q���P�P���P�R���P�V���P�X�̖ł͂���܂���̂ŏ����܂��B
�]����
�Q�ƂP�P�ƂP�O�O�P�Ƃ��̐��̂P�O�{�A�P�O�O�{�A�P�O�O�O�{�A�P�O�O�O�O�{�ɂȂ�܂��B
���������ĂR�~�T���P�T�ɂȂ�܂��B
�E����17
�i�y���l�|���F�X���[�N�}���j
(1)
20 ! = 218*38*54*72*11*13*17*19
(2)
20!= 218*38*54*72*11*13*17*19 �Ȃ̂ŁA3�搔�̐��́A�A�A
�@18/3=6
�@8/3=2
�@4/3=1�@����A�A�A
7*3*2=42 �i�����1���܂܂��j
(3)
20=22*5 �Ȃ̂ŁA
�@20 ! �̖̌��[19 ! �̖̐�
=(19*5-17*4)*9*3*24
=27*9*3*24
=36*24 ��
(4)
5��4�Ȃ̂ŁA
2,20,200,2000,20000
11,110,1100,11000,110000
1001=7*11*13,10010,100100,1001000,10010000
72* 11 * 13 * 17 * 19 = 2263261 �Ȃ̂ŁA
10001,100001�܂łɂ͂Ȃ��B
101 �͂Ȃ��B
�ȏォ��A
2,11,1001 ��3��� x 5��15��
�E����18
�i�y���l�|���F��ӂ����̂炢��������j

�i�P�j
20�I��1�~2�~3�~4�~5�~6�~7�~8�~9�~10�~11�~12�~13�~14�~+15�~16�~17�~18�~19�~20
��2�~3�~22�~5�~2�3�~7�~23�~32�~2�5�~11�~22�3�~13�~2�7�~3�5�~24�~17�~2�32�~19�~22�5
��218�~38�~54�~72�~11�~13�~17�~19
�i�Q�j
23��A�A33��B�A53��C�Ƃ�����
20�I�̖ŗ������̍ő�́AA6�~B2�~C1
������A7�~3�~2��42��
�i�R�j
20�I�̖̌��́A19�~9�~5�~3�~2�~2�~2�~2��41040
19�I��216�~38�~53�~72�~11�~13�~17�~19���
19�I�̖̌��́A17�~9�~4�~3�~2�~2�~2�~2��29376
������A�@41040�|29376��11664��24�~36
�i�S�j
�e���̘a��2�ɂȂ鐔�́A
�@���j�ŏ�ʂ̐�����2�ő��̐�����0�ł���ꍇ
�@���j1��2�ő��͑S��0�ł���ꍇ
�Ƃɂ킩��܂��B
���j�̏ꍇ�A20�I�̖�
�@2�C20�C200�C2000�C20000
�@2��2
�@20��2�~(2�~5)
�@200��2�~(2�~5)2
�@2000��2�~(2�~5)3
�@20000��2�~(2�~5)4
�ȏ�̂T��
���j�̏ꍇ��
11�C101�C110�C1001�C1010�C1100�C�E�E�E�E�E�E�Ȃǂł��B
| �@ | 11 | �f�� | �� | �� |
| �@ | 101 | �f�� | �� | �~ |
| �@ | 110 | ��11�~(2�~5) | �� | �� |
| �@ | 1001 | ��11�~7�~13 | �� | �� |
| �@ | 1010 | ��101�~(2�~5) | �� | �~ |
| �@ | 1100 | ��11�~(2�~5)2 | �� | �� |
| �@ | 10001 | ��73�~137 | �� | �~ |
| �@ | 10010 | ��11�~7�~13�~(2�~5) | �� | �� |
| �@ | 10100 | ��101�~(2�~5)2 | �� | �~ |
| �@ | 11000 | ��11�~(2�~5)3 | �� | �� |
| �@ | 100001 | ��11�~9091 | �� | �~ |
| �@ | 100010 | ��73�~137�~(2�~5) | �� | �~ |
| �@ | 100100 | ��11�~7�~13�~(2�~5)2 | �� | �� |
| �@ | 101000 | ��101�~(2�~5)3 | �� | �~ |
| (��) | 110000 | ��11�~(2�~5)4 | �� | �� |
| �@ | 1000001 | ��101�~9901 | �� | �~ |
| �@ | 1000010 | ��11�~9091�~(2�~5) | �� | �~ |
| �@ | 1000100 | ��73�~137�~(2�~5)2 | �� | �~ |
| �@ | 1001000 | ��11�~7�~13�~(2�~5)3 | �� | �� |
| �@ | 1010000 | ��101�~(2�~5)4 | �� | �~ |
| �@ | 1100000 | ��11�~(2�~5)5 | �� | �~ |
| �@ | 10000001 | ��11�~909091 | �� | �~ ��909091��20�I�̈����͂���܂��� |
| �@ | 10000010 | ��101�~9901�~(2�~5) | �� | �~ |
| �@ | 10000100 | ��11�~9091�~(2�~5)2 | �� | �~ |
| �@ | 10001000 | ��73�~137�~(2�~5)3 | �� | �~ |
| (��) | 10010000 | ��11�~7�~13�~(2�~5)4 | �� | �� |
| �@ | 10100000 | ��101�~(2�~5)5 | �� | �~ |
| �@ | 11000000 | ��11�~(2�~5)6 | �� | �~ |
| �@ | 100000001 | ��17�~58823535 | �� | �~�@�@��5882353��20�I�̈����͂���܂��� |
| �@ | 100000010 | ��11�~909091�~(2�~5) | �� | �~ |
| �@ | 100000100 | ��101�~9901�~(2�~5)2 | �� | �~ |
| �@ | 100001000 | ��11�~9091�~(2�~5)3 | �� | �~ |
| �@ | 100010000 | ��73�~137�~(2�~5)4 | �� | �~ |
| �@ | 100100000 | ��11�~7�~13�~(2�~5)5 | �� | �~ |
| �@ | 101000000 | ��101�~(2�~5)6 | �� | �~ |
| �@ | 110000000 | ��11�~(2�~5)7 | �� | �~ |
| �@ | �E�E�E�E |
11�~10k�̌`�́A(��)���ő�ł��B
101�~10k�̌`�́A101���f���Ȃ̂ł��߂ł��B
1001�~10k�̌`�́A(��)���ő�ł��B
10001�~10k�̌`�́A73�~137�������Ȃ̂ł��߂ł��B
100001�~10k�̌`�́A9091���f���Ȃ̂ł��߂ł��B
1000001�~10k�̌`�́A101�~9091�������Ȃ̂ł��߂ł��B
10000001�~10k�̌`�́A909091��20�I�̖������ɂ����Ȃ��̂ł��߂ł��B
100000001�~10k�̌`�́A5882353�������Ȃ̂ł��߂ł��B
����ȍ~�\���͂���܂���B
100���01�̌`�̐��i0��8�ȏ�j�́A��ł���3�̔{���ł͂���܂���B
������A2��3��5�������ɂ����܂���B
20�I�̈����ł���ȊO�̈����̐ς��v�Z����ƁA72�~11�~13�~17�~19��2263261�B
���̐��́A2263261���傫���̂ŁA20�I��7����19�̈����ł͍��܂���B
�ȏォ��A10�ł��B
���킹��ƍ��v15�ł��B
������
| �o���^�����l | �I���W | �R�E |
| �J�̖� | haya | �X���[�N�}�� |
| �̂����� | teki | kiyo |
| T_Tatekawa | ��ӂ����̂炢�������� | �]�ʔ��� |
| ���q�̗Y�L | ��̂������� | �r�n�t |
| K�̐l | BossF | �O�p��K |
�R�����g
�Q�O�I�́A�ƂĂ��傫�Ȑ��ł�����A(1)���q���g�ɂȂ��Ă���悤�ɁA
�f���������������`�ōl����Ƃ����ł��ˁB
(4)�ɂ��ẮA�u�Q�v�Ɓu�P�O�E�E�E�O�P�v����{�`�ŁA
���̂P�O���{�i�������A�O�������S�j�Ɍ��肳��܂��B
 top
top