侾係俇丏僷僀惗抧嶌傝
x偺曽掱幃
丂丂丂乥2乥2乥2x-1乥-1乥-1乥亖x2
偺0亙x亙1 偵偍偗傞夝偺屄悢傪媮傔側偝偄丅
栤戣偺弌揟
峀拞攖僴僀儗儀儖拞妛悢妛偵挧愴
嶼悢僆儕儞僺僢僋埾堳夛娔廋
島択幮僽儖乕僶僢僋僗
2000擭僼傽僀僫儖栤戣
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗岼偺柌乯
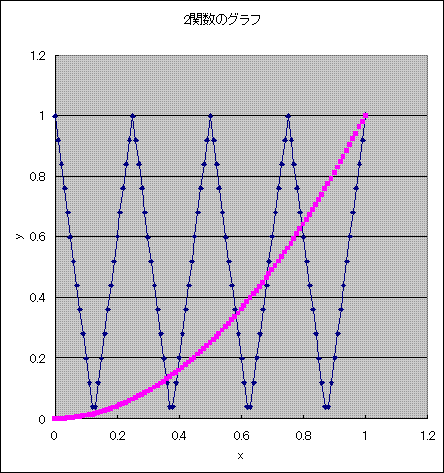
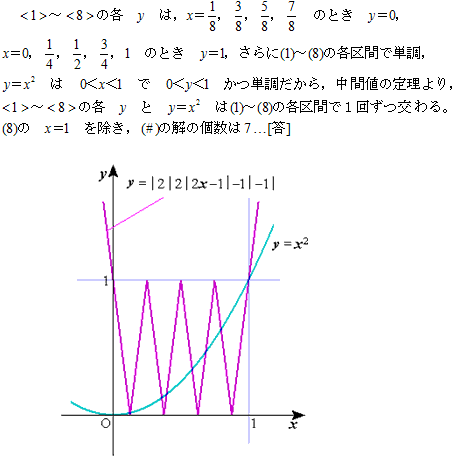
椉曽偺僌儔僼傪彂偄偰岎揰傪傕偲傔傞偲7屄乮0亙倶亙1偺斖埻乯偲側傞丅
夝摎丒偦偺2
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊偼俈捠傝偱偡丅
X2=乥俀乥俀乥俀X亅侾|亅侾乥亅侾乥
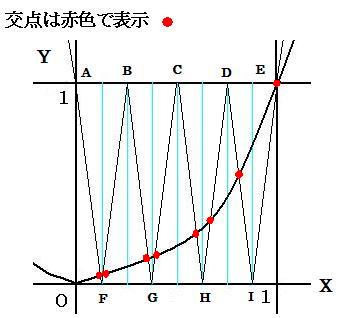
偙傟偼Y=X2偲Y=乥俀乥俀乥俀X亅侾|亅侾|亅侾乥偺僌儔僼傪昤偄偰偦偺岎揰偺悢傪悢偊傑偟偨丅
僌儔僼偺岎揰偼
慄暘 (1)A亅F 偲 (2)F亅B 偲 (3)B亅G 偲 (4)G亅C 偲 (5)C亅H 偲 (6)H亅D 偲 (7)D亅I 偲 (8)I乗E 偺俉揰偱偡偑
忦審偑侽亙X亙侾側偺偱忋婰偺 (8)I亅E 傪彍偄偨俈揰偵側傝傑偡丅廬偭偰俈捠傝偁傝傑偡丅
師偺捠傝偱偡丅
愨懳抣偺僌儔僼傪昤偒傑偡丅
夝摎丒偦偺3
乮儁儞僱亅儉丗teki乯
摎偊丂丂俈屄
僌儔僼偱峫偊傑偟偨丅
梌幃偺僌儔僼偼丄y=2x-1丂偺僌儔僼傪俁夞丄愜傝偨偨傫偱y幉曽岦偵堏摦
偝偣丄偦傟傪俀攞偡傞偲偄偆憖嶌傪孞傝曉偟偨愜傟慄僌儔僼偵側傝傑偡丅
乮偙偺偁偨傝偺條巕偑丄僞僀僩儖偺乽僷僀惗抧嶌傝乿偝側偑傜偱偡偹丅乯
堦曽丄y=x2偺僌儔僼偼丄x亜0偱扨挷憹壛偱偡偐傜丄偙偺俀偮偺僌儔僼偺
嫟桳揰偺屄悢偼丄x亙1偵偍偗傞y=x2偺孹偒偑俀傛傝彫偝偄偙偲偐傜丄x=1
傪娷傔偰俉揰偱偡丅
栤戣偼丄0亙x亙1偺斖埻偱偡偺偱丄俈屄偱偡偹丅
夝摎丒偦偺4
乮儁儞僱亅儉丗柪巕偺梇擫乯
0亙x亙1偺斖埻偱偼丄夝偼埲壓偺俈屄丅
丂0.123105626
丂0.127016654
丂0.358898944
丂0.394448725
丂0.582575695
丂0.68337521
丂0.795831523
丂丂丂乥2乥2乥2x-1乥-1乥-1乥亖x俀
応崌暘偗偺搒崌忋丄埲壓偺偲偍傝幃侾乣幃俇傪掕媊偡傞丅
幃侾亖 丂丂丂2x-1丂丂
幃俀亖丂丂丂乥2x-1乥丂丂
幃俁亖 丂丂2乥2x-1乥-1丂丂丂丂亖2乮幃俀乯-1
幃係亖丂 乥2乥2x-1乥-1乥丂
幃俆亖丂2乥2乥2x-1乥-1乥-1丂丂亖2乮幃係乯-1
幃俇亖乥2乥2乥2x-1乥-1乥-1乥丂亖梌幃偺嵍曈
- x=1/2偺偲偒乮嵍曈乯2x-1亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 0亙x亙1/2偺偲偒幃侾亙0傛傝幃俀亖1-2x丄幃俁亖1-4x
- x=1/4偺偲偒乮嵍曈乯幃俁亖1-4x亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 0亙x亙1/4偺偲偒幃俁亜0傛傝幃係亖1-4x丄幃俆亖1-8x
- x=1/8偺偲偒乮嵍曈乯幃俆亖1-8x亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 0亙x亙1/8偺偲偒幃俆亜0傛傝幃俇亖1-8x亖x俀丄傛傝x俀+8x-1=0
丂丂丂x=0.123105626丄-8.123105626傛傝夝侾屄
- 1/8亙x亙1/4偺偲偒幃俆亙0傛傝幃俇亖8x-1亖x俀丄傛傝x俀-8x+1=0
丂丂丂x=7.872983346丄0.127016654傛傝夝侾屄
- x=1/8偺偲偒乮嵍曈乯幃俆亖1-8x亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 1/4亙x亙1/2偺偲偒幃俁亙0傛傝幃係亖4x-1丄幃俆亖8x-3
- x=3/8偺偲偒乮嵍曈乯幃俆亖8x-3亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 1/4亙x亙3/8偺偲偒幃俆亙0傛傝幃俇亖-8x+3亖x俀丄傛傝x俀+8x-3=0
丂丂丂x=0.358898943540674丄-8.35889894354067傛傝丄夝侾屄
- 3/8亙x亙1/2偺偲偒幃俆亜0傛傝幃俇亖8x-3亖x俀丄傛傝x俀-8x+3=0
丂丂丂x=7.60555127546399丄0.394448724536011傛傝丄夝侾屄
- x=3/8偺偲偒乮嵍曈乯幃俆亖8x-3亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- x=1/4偺偲偒乮嵍曈乯幃俁亖1-4x亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 1/2亙x亙 1 偺偲偒幃侾亜0傛傝幃俀亖2x-1丄幃俁亖4x-3
- x=3/4偺偲偒乮嵍曈乯幃俁亖4x-3亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 1/2亙x亙<3/4偺偲偒幃俁亙0傛傝幃係亖3-4x丄幃俆亖5-8x
- x=5/8偺偲偒乮嵍曈乯幃俆亖5-8x亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 1/2亙x亙5/8偺偲偒幃俆亙0傛傝幃俇亖-8x+5亖x俀丄傛傝x俀+8x-5=0
丂丂丂x=0.58257569495584丄-8.58257569495584傛傝丄夝侾屄
- 5/8亙x亙3/4偺偲偒幃俆亜0傛傝幃俇亖8x-5亖x俀丄傛傝x俀-8x+5=0
丂丂丂x=7.3166247903554丄0.6833752096446傛傝丄夝侾屄
- x=5/8偺偲偒乮嵍曈乯幃俆亖5-8x亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 3/4亙x亙1 偺偲偒幃俁亜0傛傝幃係亖4x-3丄幃俆亖8x-7
- x=7/8偺偲偒乮嵍曈乯幃俆亖8x-7亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- 3/4亙x亙7/8偺偲偒幃俆亙0傛傝幃俇亖-8x+7亖x俀丄傛傝x俀+8x-7=0
丂丂丂x=0.795831523312719丄-8.79583152331272傛傝丄夝侾屄
- 7/8亙x亙 1 偺偲偒幃俆亜0傛傝幃俇亖8x-7亖x俀丄傛傝x俀-8x+7=0
丂丂丂x=7丄1傛傝丄夝側偟
- x=7/8偺偲偒乮嵍曈乯幃俆亖8x-7亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
- x=3/4偺偲偒乮嵍曈乯幃俁亖4x-3亖0傛傝惍悢丄乮塃曈乯旕惍悢偲側傝丄夝側偟
夝摎丒偦偺5
乮儁儞僱亅儉丗僆儎僕乯
愨懳抣偺応崌暘偗側傫偰夰偐偟偄偱偡丅
乮嘥乯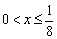 偺偲偒丂
乮侾乯偺幃偼丄
偺偲偒丂
乮侾乯偺幃偼丄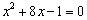 丂丂丂
亪丂
丂丂丂
亪丂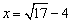
乮嘦乯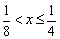 偺偲偒丂
乮侾乯偺幃偼丄
偺偲偒丂
乮侾乯偺幃偼丄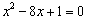 丂丂丂
亪丂
丂丂丂
亪丂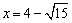
乮嘨乯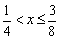 偺偲偒丂
乮侾乯偺幃偼丄
偺偲偒丂
乮侾乯偺幃偼丄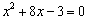 丂丂丂
亪丂
丂丂丂
亪丂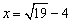
乮嘩乯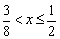 偺偲偒丂
乮侾乯偺幃偼丄
偺偲偒丂
乮侾乯偺幃偼丄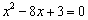 丂丂丂
亪丂
丂丂丂
亪丂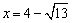
乮嘪乯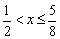 偺偲偒丂
乮侾乯偺幃偼丄
偺偲偒丂
乮侾乯偺幃偼丄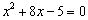 丂丂丂
亪丂
丂丂丂
亪丂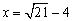
乮嘫乯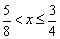 偺偲偒丂
乮侾乯偺幃偼丄
偺偲偒丂
乮侾乯偺幃偼丄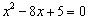 丂丂丂
亪丂
丂丂丂
亪丂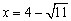
乮嘮乯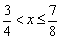 偺偲偒丂
乮侾乯偺幃偼丄
偺偲偒丂
乮侾乯偺幃偼丄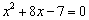 丂丂丂
亪丂
丂丂丂
亪丂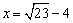
乮嘯乯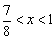 偺偲偒丂
乮侾乯偺幃偼丄
偺偲偒丂
乮侾乯偺幃偼丄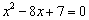 丂丂丂
亪丂丂夝側偟
丂丂丂
亪丂丂夝側偟
乮嘥乯乣乮嘯乯傛傝丂丂丂亪丂俈屄
夝摎丒偦偺6
乮儁儞僱亅儉丗偺偭偙傫乯
- x亝0.125偺帪丂丂1-8x=x2 丂 x=-4+
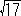 =0.123丒丒丒丂丂丂揔
=0.123丒丒丒丂丂丂揔
- 0.125亙x亝0.25偺帪丂丂8x-1=x2 x=4-
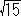 =0.127丒丒丒丂丂丂揔
=0.127丒丒丒丂丂丂揔
- 0.25亙x亙0.375偺帪丂丂丂3-8x=x2 x=-4+
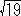 =0.358丒丒丒丂丂丂揔
=0.358丒丒丒丂丂丂揔
- 0.375亝x亙0.5偺帪丂丂丂8x-3=x2 x=4-
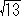 =0.394丒丒丒丂丂丂揔
=0.394丒丒丒丂丂丂揔
- 0.5亝倶亝0.625偺帪丂丂丂5-8x=x2 x=-4+
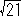 =0.582丒丒丒丂丂丂揔
=0.582丒丒丒丂丂丂揔
- 0.625亙x亙0.75偺帪丂丂丂8x-5=x2 x=4-
 =0.683丒丒丒丂丂丂揔
=0.683丒丒丒丂丂丂揔
- 0.75亝x亙0.875偺帪丂丂丂7-8x=x2 x=-4+
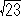 =0.795丒丒丒丂丂丂揔
=0.795丒丒丒丂丂丂揔
- 0.875亝x偺帪丂丂丂8x-7=x2 x=1,x=7 晄揔
丂丂乮摎偊乯夝偺屄悢偼7
儖-僩偺拞偑11丄13丄15丄17丄19丄21丄23偲側傝嫽枴怺偄偲偙傠偱偡
夝摎丒偦偺7
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
嵍曈偼捈慄丄塃曈偼 x2 (02=0丄12=1)側偺偱丄
嵍曈偑丄x=0 偱儅僀僫僗丄x=1 偱1傛傝戝偒偄偲偒丄嵍曈偑0傛傝戝偒偔丄x=1 偱1傛傝彫偝偗傟偽1揰偱岎傢傞丅
+-偁傞偺偱丄23=8 屄偺曽掱幃偱峫偊傟偽偄偄偲巚偆偺偱丄丄丄
- +++ 偺偲偒丄
丂8x-7=x2
丂x=0 偺偲偒丄嵍曈= -7丄x=1 偺偲偒丄嵍曈=1
丂偮傑傝丄x=1 偺1揰偱岎傢傞偺偱丄0亙x亙1 傪枮偨偝側偄丅
- ++- 偺偲偒丄
丂-8x+1=x2
丂x=0 偱丄嵍曈=1丄x=1 偱丄嵍曈=-7
丂偮傑傝丄0亙x亙1 偺娫偱1揰偱岎傢傞丅
- +-- 偺偲偒丄
丂8x-3=x2
丂嵍曈偼丄-3 偲5 側偺偱丄1揰岎傢傞丅
- +-+ 偺偲偒丄
丂-8x+5=x2
丂嵍曈偼丄5 偲-3 側偺偱丄1揰岎傢傞丅
- --- 偺偲偒丄
丂-8x+3=x2
丂嵍曈偼丄3 偲-5 側偺偱丄1揰岎傢傞丅
- --+ 偺偲偒丄
丂8x-5=x2
丂嵍曈偼丄-5 偲3側偺偱丄1揰岎傢傞丅
- -+- 偺偲偒丄
丂8x-1=x2
丂嵍曈偼丄-1 偲7側偺偱丄1揰岎傢傞丅
- -++ 偺偲偒丄
丂-8x+7=x2
丂嵍曈偼丄7 偲-1側偺偱丄1揰岎傢傞丅
埲忋傛傝丄7揰 偱偄偄偺偐側 ^^v
夝摎丒偦偺8
乮儁儞僱亅儉丗僄儖僪僗乯
夝摎丂 嵍曈偺愨懳抣傪弴偵奜偡偲丂
| (1) 1/2亝x亙1偺偲偒 | [2[4x-3 ]-1] |
| 丂丂(1-1) 3/4亝x亙1偺偲偒 | 丂[8x-7 ] |
| 丂丂丂丂(1-1-1) 7/8亝x亙1偺偲偒 | 丂丂丂 8x-7 |
| 丂丂丂丂(1-1-2) 3/4亝x亙7/8偺偲偒 | 丂丂丂-8x+7 |
| 丂丂(1-2) 1/2亝x亙3/4偺偲偒 | 丂[-8x+5] |
| 丂丂丂丂(1-2-1) 5/8亝x亙3/4 偺偲偒 | 丂丂丂 8x-5 |
| 丂丂丂丂(1-2-2) 1/2亝x亙5/8偺偲偒 | 丂丂丂-8x+5 |
| (2) 0亙x亙1/2偺偲偒 | [2[-4x+1]-1] |
| 丂丂(2-1) 1/4亝x亙1/2偺偲偒 | 丂[ 8x-3 ] |
| 丂丂丂丂(2-1-1) 3/8亝x亙1/2偺偲偒 | 丂丂丂 8x-3 |
| 丂丂丂丂(2-1-2) 1/4亝x亙3/8偺偲偒 | 丂丂丂-8x+3 |
| 丂丂(2-2) 0亙x亙1/4偺偲偒 | 丂[-8x+1] |
| 丂丂丂丂(2-2-1) 1/8亝x亙1/4偺偲偒 | 丂丂丂 8x-1 |
| 丂丂丂丂(2-2-2) 0亙x亙1/8偺偲偒 | 丂丂丂-8x+1 |
y亖[2[2[2x-1 ]-1]-1]丒丒丒丒(1)偲y=x2丒丒丒丒(2)偺僌儔僼傪偐偒丄0亙x亙1偱偺岎揰偺屄悢傪悢偊傞偲俈屄懚嵼偡傞丅
夝摎丒偦偺9
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
摎偊丗7屄
f(X)亖倃2亅乥2乥2乥2倃-1乥-1乥-1乥亖侽偲偡傞偲
7/8亝倃亙0 丂 丂倃2亅8倃亄俈亖侽丂倃亖侾丆俈丂丂丂丂丂夝側偟
3/4亝倃亙7/8丂丂倃2亄8倃亅俈亖侽丂倃亖亅係亇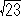 丂丂亄偺曽偺傒
丂丂亄偺曽偺傒
5/8亝倃亙3/4丂丂倃2亅8倃亄俆亖侽丂倃亖丂係亇 丂丂亅偺曽偺傒
丂丂亅偺曽偺傒
1/2亝倃亙5/8丂丂倃2亄8倃亅俆亖侽丂倃亖亅係亇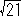 丂丂亄偺曽偺傒
丂丂亄偺曽偺傒
3/8亝倃亙1/2丂丂倃2亅8倃亄俁亖侽丂倃亖丂係亇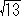 丂丂亅偺曽偺傒
丂丂亅偺曽偺傒
1/4亝倃亙3/8丂丂倃2亄8倃亅俁亖侽丂倃亖亅係亇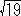 丂丂亄偺曽偺傒
丂丂亄偺曽偺傒
1/8亝倃亙1/4丂丂倃2亅8倃亄侾亖侽丂倃亖丂係亇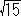 丂丂亅偺曽偺傒
丂丂亅偺曽偺傒
0亙倃亙1/8 丂丂 倃2亄8倃亅侾亖侽丂倃亖亅係亇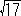 丂丂亄偺曽偺傒
丂丂亄偺曽偺傒
夝傪媮傔偢偵屄悢傪媮傔傞応崌偼f(0)亙0丄f(1/8)亜0傛傝偙偺娫偵侾屄偺傛
偆偵壓婰丄嫬栚偺惓晧偑媡揮偟偰偄偔偺偱奺侾屄丅
f(1/4)亙0丂f(3/8)亜0丂f(1/2)亙0丂f(5/8)亜0丂f(3/4)亙0
f(7/8)亜0丂f(1)亖侽
嵟屻偺嬫娫偺傒夝側偟偑媮傑傝傑偡偹
夝摎丒偦偺10
乮儁儞僱亅儉丗haya乯
僷僀惗抧嶌傝 偺夝偼 7屄偱偡丅
亂夝偒曽亃
愨懳抣偺婰崋偱幃偑嶰廳偵僱僗僩偝傟偰偄傞偐傜丄
拞恎偑惓偵側傞応崌偲晧偵側傞応崌偦傟偧傟2偮偵応崌暘偗偝傟崌寁 23=8 偵応崌暘偗偝傟傞丅
偦傟偧傟偵偮偄偰夝偑偁傞偙偲傪妋偐傔傞偲丄


傛傝丄夝偼 7屄偲側傞丅
夝摎丒偦偺11
乮儁儞僱亅儉丗昹揷柧枻乯
丂乥俀乥俀乥俀倶亅侾乥亅侾乥亅侾乥亖倶俀乮侽亙倶亙侾乯
丂乽乥倶乥亖倎丂佁丂倶亞侽偺偲偒倶亖倎丆倶亙侽偺偲偒倶亖亅倎乿
傪巊偆偲戝曄偦偆側偺偱丆
丂乽乥倶乥亖倎丂佁丂倶亖亇倎偐偮倎亞侽乿
傪夝摎曽恓偲偡傞丏
丂梌曽掱幃偐傜丆
丂丂俀乥俀乥俀倶亅侾乥亅侾乥亅侾亖亇倶俀
丂丂亪乥俀乥俀倶亅侾乥亅侾乥亖(侾亇倶俀)乛俀
i). 乥俀乥俀倶亅侾乥亅侾乥亖(侾亄倶俀)乛俀乮亜侽乯偺帪丆
丂丂俀乥俀倶亅侾乥亅侾亖亇(侾亄倶俀)乛俀
丂丂亪乥俀倶亅侾乥亖{侾亇(侾亄倶俀)乛俀}乛俀
i).-i). 乥俀倶亅侾乥亖{侾亄(侾亄倶俀)乛俀}乛俀亖(俁亄倶俀)乛係乮亜侽乯偺帪丆
丂丂係(俀倶亅侾)亖亇(俁亄倶俀)
i).-i).-i). 係(俀倶亅侾)亖俁亄倶俀偺帪丆
丂丂倶俀亅俉倶亄俈亖侽
丂丂亪(倶亅侾)(倶亅俈)亖侽
丂偙傟偼侽亙倶亙侾偵斀偡傞丏
i).-i).-ii). 係(俀倶亅侾)亖亅(俁亄倶俀)偺帪丆
丂丂倶俀亄俉倶亅侾亖侽
丂丂亪倶亖亅係亇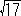
丂亅係亅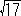 亙侽偱偁傝丆
亙侽偱偁傝丆
丂丂亅係亄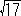 亖
亖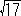 亅
亅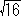 亜侽
亜侽
丂丂(亅係亄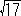 )亅侾
亖
)亅侾
亖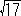 亅俆
亖
亅俆
亖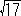 亅
亅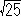 亙侽
亙侽
丂丂亪侽亙亅係亄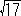 亙侾
亙侾
丂丂亪倶亖亅係亄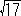
i).-ii). 乥俀倶亅侾乥亖{侾亅(侾亄倶俀)乛俀}乛俀亖(侾亅倶俀)乛係偺帪丆
丂侽亙倶亙侾偐傜丆(侾亅倶俀)乛係亜侽偲側傞丏
丂偙偺帪丆
丂丂係(俀倶亅侾)亖亇(侾亅倶俀)
i).-ii).-i). 係(俀倶亅侾)亖侾亅倶俀偺帪丆
丂丂倶俀亄俉倶亅俆亖侽
丂丂亪倶亖亅係亇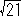
丂亅係亅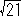 亙侽偱偁傝丆
亙侽偱偁傝丆
丂丂亅係亄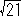 亖
亖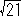 亅
亅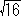 亜侽
亜侽
丂丂(亅係亄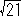 )亅侾
亖
)亅侾
亖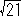 亅俆
亖
亅俆
亖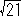 亅
亅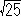 亙侽
亙侽
丂丂亪侽亙亅係亄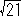 亙侾
亙侾
丂丂亪倶亖亅係亄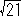
i).-ii).-ii). 係(俀倶亅侾)亖亅(侾亅倶俀)偺帪丆
丂丂倶俀亅俉倶亄俁亖侽
丂丂亪倶亖係亇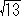
丂係亄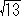 亜侾偱偁傝丆
亜侾偱偁傝丆
丂丂係亅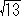 亖
亖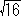 亅
亅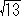 亜侽
亜侽
丂丂(係亅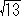 )亅侾
亖俁亅
)亅侾
亖俁亅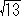 亖
亖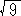 亅
亅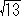 亙侽
亙侽
丂丂亪侽亙係亅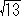 亙侾
亙侾
丂丂亪倶亖係亅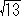
ii). 乥俀乥俀倶亅侾乥亅侾乥亖(侾亅倶俀)乛俀乮亜侽乯偺帪丆
丂丂俀乥俀倶亅侾乥亅侾亖亇(侾亅倶俀)乛俀
丂丂亪乥俀倶亅侾乥亖{侾亇(侾亅倶俀)乛俀}乛俀
ii).-i). 乥俀倶亅侾乥亖{侾亄(侾亅倶俀)乛俀}乛俀亖(俁亅倶俀)乛係偺帪丆
丂侽亙倶亙侾偐傜丆(俁亅倶俀)乛係亜侽偲側傞丏
丂偙偺帪丆
丂丂係(俀倶亅侾)亖亇(俁亅倶俀)
ii).-i).-i). 係(俀倶亅侾)亖俁亅倶俀偺帪丆
丂丂倶俀亄俉倶亅俈亖侽
丂丂亪倶亖亅係亇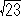
丂亅係亅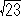 亙侽偱偁傝丆
亙侽偱偁傝丆
丂丂亅係亄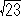 亖
亖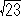 亅
亅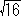 亜侽
亜侽
丂丂(亅係亄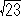 )亅侾亖
)亅侾亖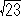 亅俆
亖
亅俆
亖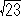 亅
亅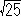 亙侽
亙侽
丂丂亪侽亙亅係亄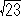 亙侾
亙侾
丂丂亪倶亖亅係亄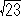
ii).-i).-ii). 係(俀倶亅侾)亖亅(俁亅倶俀)偺帪丆
丂丂倶俀亅俉倶亄侾亖侽
丂丂亪倶亖係亇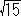
丂係亄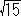 亜侾偱偁傝丆
亜侾偱偁傝丆
丂丂係亅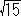 亖
亖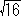 亅
亅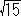 亜侽
亜侽
丂丂(係亅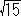 )亅侾亖俁亅
)亅侾亖俁亅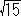 亖
亖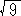 亅
亅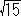 亙侽
亙侽
丂丂亪侽亙係亅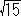 亙侾
亙侾
丂丂亪倶亖係亅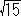
ii).-ii). 乥俀倶亅侾乥亖{侾亅(侾亅倶俀)乛俀}乛俀亖(侾亄倶俀)乛係乮亜侽乯偺帪丆
丂丂係(俀倶亅侾)亖亇(侾亄倶俀)
ii).-ii).-i). 係(俀倶亅侾)亖侾亄倶俀偺帪丆
丂丂倶俀亅俉倶亄俆亖侽
丂丂亪倶亖係亇
丂係亄 亜侾偱偁傝丆
亜侾偱偁傝丆
丂丂係亅 亖
亖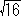 亅
亅 亜侽
亜侽
丂丂(係亅 )亅侾
亖俁亅
)亅侾
亖俁亅 亖
亖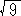 亅
亅 亙侽
亙侽
丂丂亪侽亙係亅 亙侾
亙侾
丂丂亪倶亖係亅
ii).-ii).-ii). 係(俀倶亅侾)亖亅(侾亄倶俀)偺帪丆
丂丂倶俀亄俉倶亅俁亖侽
丂丂亪倶亖亅係亇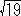
丂亅係亅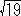 亙侽偱偁傝丆
亙侽偱偁傝丆
丂丂亅係亄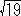 亖
亖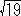 亅
亅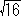 亜侽
亜侽
丂丂(亅係亄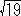 )亅侾
亖
)亅侾
亖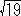 亅俆
亖
亅俆
亖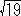 亅
亅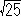 亙侽
亙侽
丂丂亪侽亙亅係亄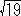 亙侾
亙侾
丂丂亪倶亖亅係亄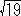
丂傑偲傔傞偲丆
丂丂倶亖亅係亄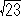 丆
亅係亄
丆
亅係亄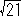 丆
亅係亄
丆
亅係亄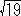 丆
亅係亄
丆
亅係亄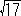 丆
係亅
丆
係亅 丆
係亅
丆
係亅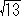 丆
係亅
丆
係亅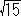
偺俈屄偁傞丏
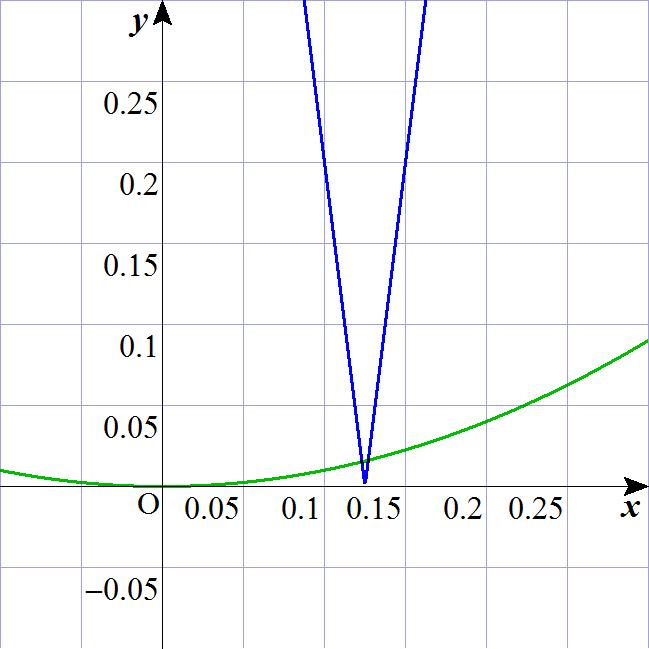
丂幚嵺俧俼俙俹俤俽傪巊偭偰丆倖(倶)亖乥俀倶亅侾乥偲偟偰丆僌儔僼倷亖倖(倖(倖(倶)))乮惵怓乯丆倷亖倶俀乮椢怓乯傪恾帵偟偰傒傞偲丆
侽亙倶亙侾偺晹暘偱俈屄偺岎揰偑懚嵼偡傞帠偑暘偐傞丏
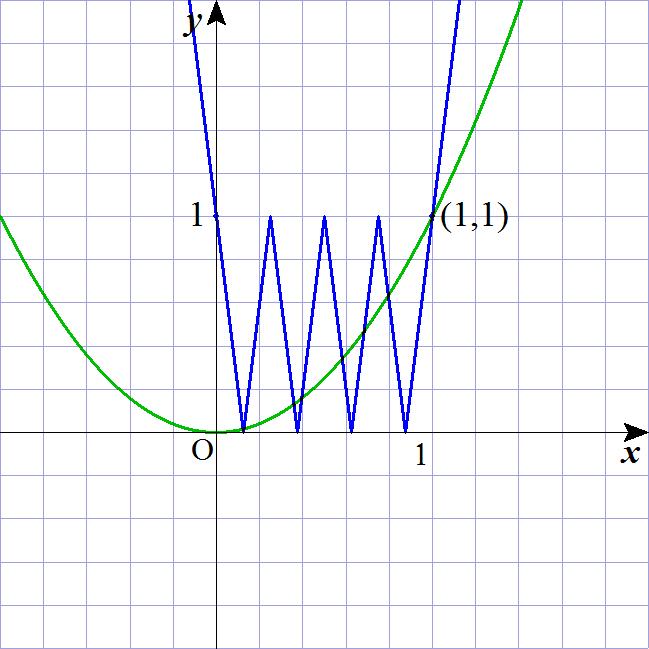
丂擮偺堊丆亅侽.侾亝倶亝侽.俁丆亅侽.侾亝倷亝侽.俁偺斖埻偵奼戝偟偨僌儔僼傪恾帵偟偰傕丆
妋偐偵偙偺斖埻偱俀揰偱岎傢偭偰偄傞帠偑暘偐傞丏
夝摎丒偦偺12
乮儁儞僱亅儉丗揮埵斀墳乯
f(x)=乥2乥2乥2x-1乥-1乥-1乥偲偡傞丅
侾丏2x-1亞0偺応崌丗1/2亝x亙1
丂丂丂f(x)=乥2乥2(2x-1)-1乥-1乥
丂丂丂丂丂=乥2乥4x-3乥-1乥
偙偙偱丄
丂丒4x-3亞0偺応崌丗3/4亝x亙1
丂丂丂f(x)=乥2(4x-3)-1乥
丂丂丂丂丂=乥8x-7乥
偝傜偵丄
丂丂丂丒8x-7亞0偺応崌丗偮傑傝丄7/8亝x亙1偱丄f(x)=8x-7
丂丂丂丒8x-7亙0偺応崌丗偮傑傝丄3/4亝x亙7/8偱丄f(x)=7-8x
丂丒4x-3亙0応崌丗1/2亝x亙3/4
丂丂丂f(x)=乥2(3-4x)-1乥
丂丂丂丂丂=乥5-8x乥
偝傜偵丄
丂丂丂丒5-8x亞0偺応崌丗偮傑傝丄1/2亝x亝5/8偱丄f(x)=5-8x
丂丂丂丒5-8x亙0偺応崌丗偮傑傝丄5/8亙x亙3/4偱丄f(x)=8x-5
俀丏2x-1亙0偺応崌偵偮偄偰傕摨條偵張棟偟丄侾丏偺寢壥偲嫟偵惍棟偡傞偲埲壓偺捠傝丅
廬偭偰丄0亙x亙1傪枮偨偡f(x)=x2偺夝傪媮傔傟偽椙偄丅
| x | f(x) |
|---|---|
| 0亙x亝1/8 | 1-8x |
| 1/8亙x亝1/4 | 8x-1 |
| 1/4亙x亙3/8 | 3-8x |
| 3/8亝x亙1/2 | 8x-3 |
| 1/2亝x亙5/8 | 5-8x |
| 5/8亙x亙3/4 | 8x-5 |
| 3/4亝x亙7/8 | 7-8x |
| 7/8亝x亙1 | 8x-7 |

夝摎丒偦偺13
乮儁儞僱亅儉丗嶰妏掕婯乯

夝摎丒偦偺14
乮儁儞僱亅儉丗T_Tatekawa乯
栤戣偺戣柤偺堄枴偼丆僌儔僼傪昤偄偰弶傔偰暘偐傝傑偟偨丏
y=x2 偲 y=| 2 | 2 | 2x-1 | -1 | -1 | 偺僌儔僼傪揧晅偟傑偡丏
暔棟偱傕丆椺偊偽僀儞僋傪悈偵悅傜偟偨帪偺奼嶶偺榖偱丆
乽僷僀偙偹曄姺乿偲偄偆榖偑弌偰偒傑偡丏
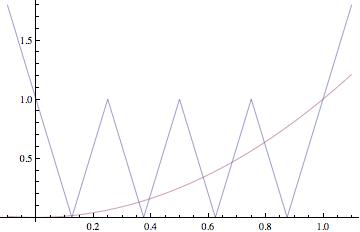
0亙x亙1 偺夝傪媮傔偰丆傂偨偡傜応崌暘偗偟偰偄偒傑偡丏
1) | 2 | 2 (2x-1) -1 | -1 | = x2 (x=> 1/2)
丂丂丂| 2 | 4x-3 | -1 | = x2
1A) | 2 (4x-3) -1 | = x2 (x => 3/4)
丂丂丂 | 8x-7 | = x2
1Aa) 8x-7 = x2 (x => 7/8)
丂丂丂夝偼 x=1, 7仺忦審偐傜柍偟
1Ab) -8x+7 = x2 (7/8 -> x => 3/4)
丂丂丂夝偼 x=-4+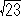 , -4-
, -4-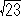
丂丂丂仺揔偟偨夝偼 x=-4+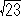
1B) | 2 (-4x+3) -1 | = x2 (3/4 => x => 1/2)
丂丂丂| -8x + 5 | = x2
1Ba) -8x+5 = x2 (5/8 => x => 1/2)
丂丂丂夝偼 x=-4+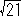 , -4-
, -4-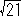
丂丂丂仺揔偟偨夝偼 x=-4+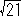
1Bb) 8x-5 = x2 (3/4 => x => 5/8)
丂丂丂夝偼 x=4+ , 4-
, 4-
丂丂丂仺揔偟偨夝偼 x=4-
2) | 2 | 2 (-2x+1) -1 | -1 | = x2 (x <= 1/2)
丂丂丂| 2 | -4x+1 | -1 | = x2
丂丂丂2A) | 2 (-4x+1) -1 | = x2 (x <= 1/4)
丂丂丂| -8x+1 | = x2
2Aa) -8x+1 = x2 (1/8 => x)
丂丂丂夝偼 x=-4+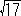 , -4-
, -4-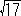
丂丂丂仺揔偟偨夝偼 x=-4+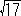
2Ab) 8x-1 = x2 (1/4 => x => 1/8)
丂丂丂夝偼 x=4-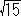 , 4+
, 4+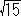
丂丂丂仺揔偟偨夝偼 x=4-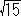
2B) | 2 (4x-1) -1 | = x2 ( 1/2 => x => 1/4 )
丂丂丂| 8x-3 | = x2
2Ba) 8x-3 = x2 (1/2 => x => 3/8)
丂丂丂夝偼 x=4-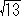 , 4+
, 4+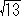
丂丂丂仺揔偟偨夝偼 x=4-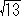
2Bb) -8x+3 = x2 (3/8 => x => 1/4)
丂丂丂夝偼 x=-4+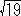 , -4-
, -4-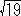
丂丂丂仺揔偟偨夝偼 x=-4+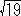
埲忋偐傜丆0亙x亙1 偵懚嵼偡傞夝偼 7屄丏
夝摎丒偦偺15
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
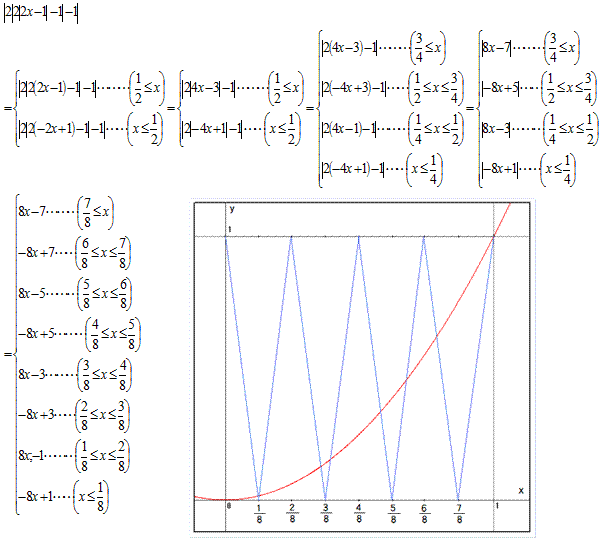
偙傟傜偺捈慄偲曻暔慄偺僌儔僼偺岎揰偺屄悢傪悢偊偰夝偼俈屄偱偡丅
夝摎俀
幃偺惉傝棫偪傪峫偊偰偁傫偪傚偙偵夝偄偰傒傑偡丅
偮傑傝丄俀攞偟偰侾傪堷偄偰愨懳抣傪偲傞偲偄偆憖嶌偑嶰廳偵側偭偰偄傑偡丅
y = | 2 x - 1 | 偺僌儔僼傪彂偄偰傒傑偡丅乮恾侾乯
愒偺曗彆慄偼丄 y = x 偺慄偱偡丅
x=0 偲 x=1 偱僌儔僼抣偼侾丄x=1/2 偱僌儔僼偺抣偼侽偵側偭偰偄傑偡丅
偙偺斖埻偱 | 2 x - 1 | 偲偄偆娭悢偼偦偆偄偆摥偒傪偟偰偄傑偡丅
師偵丄偙偺 | 2 x - 1 | 偺抣傪 倶 偲巚偭偰偙偺摥偒傪恾偵偟偰傒傑偡丅
愒偄V偺帤傪尒側偑傜僌儔僼傪彂偒傑偡丅乮恾俀乯
偝傜偵丄偙偺抣傪 x 偲巚偭偰偙偺摥偒傪恾偵偟偰傒傑偡丅
愒偄W偺帤傪尒側偑傜僌儔僼傪彂偒傑偡丅乮恾俁乯
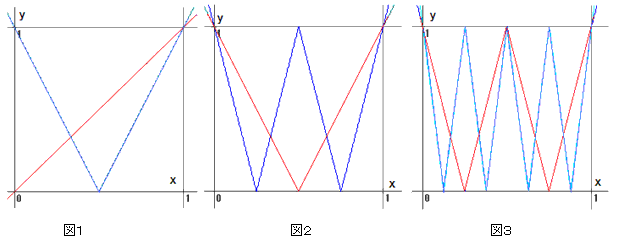
偡傞偲夝摎侾偲摨條側僌儔僼偑偱偒傑偡丅
偁偲偼曻暔慄偺僌儔僼偲廳偹偰岎揰偺屄悢傪悢偊傑偡丅
惓夝幰
| teki | 岼偺柌 | 僆儎僕 |
| 偺偭偙傫 | 昹揷柧枻 | 栭傆偐偟偺偮傜偄偍偠偝傫 |
| 僗儌乕僋儅儞 | 揮埵斀墳 | 柪巕偺梇擫 |
| T_Tatekawa | 忨偺偍偠偝傫 | 僄儖僪僗 |
| 嶰妏掕婯 | haya | 僶儖僞儞惎恖 |
僐儊儞僩
僞僀僩儖偺乽僷僀惗抧嶌傝乿傪媈栤偵巚偭偨曽傕偄傜偭偟傖傞偲巚偄傑偡丅
嵍曈傪娭悢f(x)偲偟傑偡丅
丂丂丂f(x)=乥2乥2乥2x-1乥-1乥-1乥
偙傟偼丄g(x)=乥2x-1乥偲偡傞側傜偽丄g(x)=f(f(f(x)))丄偮傑傝丄
娭悢g(x)傪俁夞崌惉偡傞偙偲偵側傝傑偡丅
偙偙偱娭悢g(x)偵偮偄偰丄僌儔僼傪昤偄偰峫偊偰傒傑偡丅
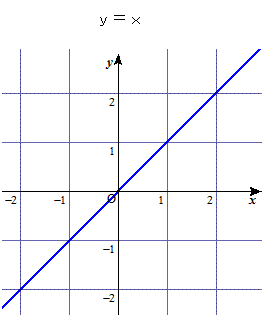
娭悢 y=x 偺僌儔僼偐傜僗僞乕僩偟傑偡丅
(1)娭悢 y=2x 偺僌儔僼偼丄y=x偺僌儔僼傪廲曽岦偵俀攞偡傞偙偲偵傛偭偰摼傜傟傑偡丅
(2)師偵丄娭悢 y=2x-1 偺僌儔僼偼丄y=2x偺僌儔僼傪廲乮壓乯曽岦偵侾偢傜偡偙偲偵傛偭偰摼傜傟傑偡丅
(3)偦偟偰丄g(x)=乥2x-1乥偺僌儔僼偼丄y=2x-1傪x幉偱忋懁偵愜傝曉偡偙偲偱摼傜傟傑偡丅
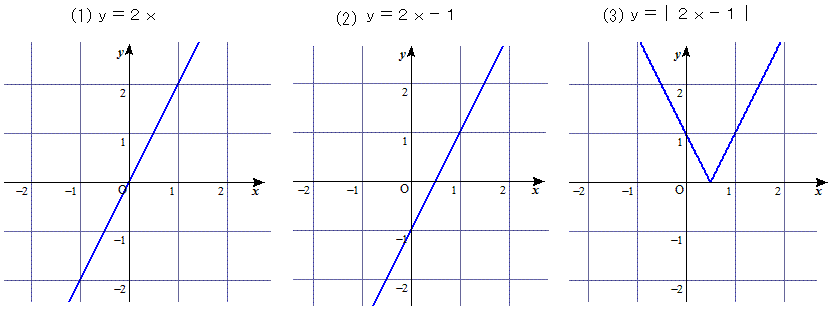
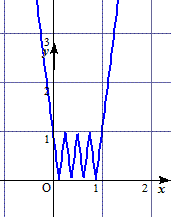
娭悢f(x)偺僌儔僼偼丄偙傟傪俁夞孞傝曉偣偽偄偄傢偗偱偡丅
偺偽偟偰丄偢傜偟偰丄愜傝曉偡丄
偙傟偭偰丄傑偝偵乽僷僀惗抧嶌傝乿偩偲巚偄傑偣傫偐丠
 top
top