侾係俁丏俆寘偺惍悢
[侾]丆[侾]丆[俀]丆[俀]丆[俁]丆[俁]丆[係]丆[係]丆[俆]丆[俆]偲彂偐傟偨10枃偺僇乕僪偑偁傞丅偙傟傜10枃偺拞偐傜俆枃傪慖傫偱丄嵍偐傜塃傊暲傋丄俆寘偺(惓偺)惍悢傪嶌傞丅
偨偲偊偽丄[侾]丆[侾]丆[俀]丆[俁]丆[係]偲暲傋傞偲丄11234偲側傞丅
偙偺傛偆偵偟偰偱偒傞俆寘偺惍悢偑俵捠傝偁傞偲偟偰丄埲壓偺栤偄偵摎偊傛丅
(1)俵偺抣傪媮傔丄俵偑10偺攞悢偱偁傞偙偲傪妋擣偣傛丅
(2)偙傟傜俵捠傝偺悢偺偆偪丄彫偝偄傎偆偐傜俵/2斣栚偺悢傪摎偊傛丅
(3)偙傟傜俵捠傝偺悢偺偆偪丄彫偝偄傎偆偐傜俵/5斣栚偺悢傪摎偊傛丅
(4)偙傟傜俵捠傝偺悢偺偆偪丄彫偝偄傎偆偐傜俵/10斣栚偺悢傪摎偊傛丅
栤戣偺弌揟
峀拞攖僴僀儗儀儖拞妛悢妛偵挧愴
嶼悢僆儕儞僺僢僋埾堳夛娔廋
島択幮僽儖乕僶僢僋僗
2004擭僼傽僀僫儖栤戣
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗昹揷丂柧枻乯
丂僄僋僙儖偺儅僋儘偱夝偒傑偟偨丏
(1) M=2220=222*10
(2) 33255
(3) 15544
(4) 13441
Option Explicit
Dim a(5) As Integer
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Call saiki(1)
'
If Cells(1, 1).Value Mod 10 = 0 Then
Cells(1, 3).Value = Cells(Cells(1, 1).Value / 2, 2).Value
Cells(1, 4).Value = Cells(Cells(1, 1).Value / 5, 2).Value
Cells(1, 5).Value = Cells(Cells(1, 1).Value / 10, 2).Value
Range("C1").Select
Else
Range("A1").Select
End If
End Sub
Sub saiki(ByVal n As Integer)
a(n) = 1
While a(n) <= 10
If onaji(n) = 0 Then
If n < 5 Then
Call saiki(n + 1)
Else
Call check(1)
End If
End If
a(n) = a(n) + 1
Wend
End Sub
Sub check(ByVal x As Integer)
Dim n As Long
Dim deta As Integer
Dim j As Integer
n = 0
For j = 1 To 5
n = n * 10 + num(a(j))
Next j
deta = 0
j = 1
While deta = 0 And j <= Cells(1, 1).Value
If n = Cells(j, 2).Value Then
deta = 1
Else
j = j + 1
End If
Wend
If deta = 0 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = n
Range("B" & Cells(1, 1).Value).Select
End If
End Sub
Private Function onaji(ByVal n As Integer) As Integer
Dim j As Integer
onaji = 0
j = 1
While onaji = 0 And j < n
If a(j) = a(n) Then
onaji = 1
Else
j = j + 1
End If
Wend
End Function
Private Function num(ByVal n As Integer) As Integer
Select Case n
Case 1, 2
num = 1
Case 3, 4
num = 2
Case 5, 6
num = 3
Case 7, 8
num = 4
Case Else
num = 5
End Select
End Function
夝摎丒偦偺2
乮儁儞僱亅儉丗挿嶈搰尨丂偐偑傒乯
乮栤侾乯
(鶣)丂A丄A丄B丄B丄C 傪慖傫偱暲傋傞僷僞乕儞(摨堦悢帤偑俀庬椶)
丂暲傋曽偼俆両亐俀両亐俀両亖俁侽捠傝
丂A丄B丄C 偺慖傃曽偼丂5俠2亊3俠1亖俁侽捠傝
丂亪俁侽亊俁侽亖俋侽侽捠傝
(鶤)丂A丄A丄B丄C丄D 傪慖傫偱暲傋傞僷僞乕儞(摨堦悢帤偑侾庬椶)
丂暲傋曽偼俆両亐俀両亖俇侽捠傝
丂A丄B丄C丄D 偺慖傃曽偼丂5俠1亊4俠3亖俀侽捠傝
丂亪俇侽亊俀侽亖侾俀侽侽捠傝
(鶥)丂A丄B丄C丄D丄E 傪慖傫偱暲傋傞僷僞乕儞(摨堦悢帤偑柍偄)
丂亪暲傋曽偼俆両亖侾俀侽捠傝
傛偭偰 俵亖俋侽侽亄侾俀侽侽亄侾俀侽亖俀俀俀侽捠傝偱偁傝丄侾侽偺攞悢偱偁傞丅
乮栤俀乯俵亐俀亖侾侾侾侽斣栚偺悢傪媮傔傞丅
(1)丂侾仯仯仯仯丂偺弴楍偵偮偄偰
丂(i)丂仯偑A丄A丄B丄B 偺応崌
丂丂丂 4俠2亊係両亐俀両亐俀両亖俁俇捠傝
丂(ii)丂仯偑A丄A丄B丄C 偺応崌
丂丂丂4俠1亊4俠2亊係両亐俀両亖俀俉俉捠傝
丂(iii)丂仯偑A丄B丄C丄D 偺応崌
丂丂丂5俹4亖侾俀侽捠傝
丂丂丂丂丂崌寁丂俁俇亄俀俉俉亄侾俀侽亖係係係捠傝 亙偙偙傑偱偱係係係斣栚亜
(2)丂俀仯仯仯仯丂偺弴楍偵偮偄偰
丂 (1)偲摨條偵係係係捠傝 亙偙偙傑偱偱俉俉俉斣栚亜
(3)丂俁仯仯仯仯丂偺弴楍偵偮偄偰
丂(i)俁侾仯仯仯偵偮偄偰
丂丂丂(傾)丂仯偑A丄A丄B 偺応崌
丂丂丂丂3俠1亊係亊俁亖俁俇捠傝
丂丂丂(僀)丂仯偑A丄B丄C 偺応崌
丂丂丂丂5俹3亖俇侽捠傝
丂丂丂丂丂寁俋俇捠傝 亙偙偙傑偱偱俋俉係斣栚亜
丂(ii)俁俀仯仯仯偵偮偄偰
丂丂丂(i)偲摨條偵俋俇捠傝 亙偙偙傑偱偱侾侽俉侽斣栚亜
丂(iii)俁俁仯仯仯偵偮偄偰
丂丂丂(傾)丂俁俁侾侾仯丂偱俁捠傝 亙偙偙傑偱偱侾侽俉俁斣栚亜
丂丂丂(僀)丂俁俁侾俀仯丂偱係捠傝 亙偙偙傑偱偱侾侽俉俈斣栚亜
丂丂丂(僂)丂俁俁侾係仯丂偱係捠傝 亙偙偙傑偱偱侾侽俋侾斣栚亜
丂丂丂(僄)丂俁俁侾俆仯丂偱係捠傝 亙偙偙傑偱偱侾侽俋俆斣栚亜
丂丂丂(僆)丂俁俁俀侾仯丂偱係捠傝 亙偙偙傑偱偱侾侽俋俋斣栚亜
丂丂丂(僇)丂俁俁俀俀仯丂偱俁捠傝 亙偙偙傑偱偱侾侾侽俀斣栚亜
丂丂丂(僉)丂俁俁俀係仯丂偱係捠傝 亙偙偙傑偱偱侾侾侽俇斣栚亜
丂丂丂(僋)丂俁俁俀俆仯丂偱係捠傝 亙偙偙傑偱偱侾侾侾侽斣栚亜
丂丂丂傛偭偰 侾侾侾侽斣栚偼丂俁俁俀俆俆丂偱偁傞丅
乮栤俁乯俵亐俆亖係係係斣栚偺悢傪媮傔傞丅
乮栤俀乯偺(1)(iii)傛傝丄侾仯仯仯仯偺嵟屻偺悢侾俆俆係係偑係係係斣栚偲側傞丅
傛偭偰丂係係係斣栚偼丂侾俆俆係係丂偱偁傞丅
乮栤係乯俵亐侾侽亖俀俀俀斣栚偺悢傪媮傔傞丅
(1)丂侾侾仯仯仯偵偮偄偰
丂(i) 仯偑A丄A丄B 偺応崌
丂丂丂4俠1亊俁亊俁亖俁俇捠傝 亙偙偙傑偱偱俁俇斣栚亜
丂(ii)仯偑A丄B丄C 偺応崌
丂丂丂4俹3亖俀係捠傝 丂丂丂丂 亙偙偙傑偱偱俇侽斣栚亜
(2)丂侾俀仯仯仯偵偮偄偰
丂(i)仯偑A丄A丄B 偺応崌
丂丂丂3俠1亊係亊俁亖俁俇捠傝 亙偙偙傑偱偱俋俇斣栚亜
丂(ii)仯偑A丄B丄C 偺応崌
丂丂丂5俹3亖俇侽捠傝 丂丂丂丂 亙偙偙傑偱偱侾俆俇斣栚亜
(3)丂侾俁仯仯仯偵偮偄偰
丂(i)侾俁侾仯仯偺応崌
丂丂丂(傾)丂仯偑A丄A 偺応崌俁捠傝 亙偙偙傑偱偱侾俆俋斣栚亜
丂丂丂(僀)丂仯偑A丄B 偺応崌4俹2亖侾俀捠傝 亙偙偙傑偱偱侾俈侾斣栚亜
丂(ii)侾俁俀仯仯偺応崌
丂丂丂(傾)丂仯偑A丄A 偺応崌俀捠傝 亙偙偙傑偱偱侾俈俁斣栚亜
丂丂丂(僀)丂仯偑A丄B 偺応崌5俹2亖俀侽捠傝 亙偙偙傑偱偱侾俋俁斣栚亜
丂(iii)侾俁俁仯仯偺応崌
丂丂丂(傾)丂仯偑A丄A 偺応崌俁捠傝 亙偙偙傑偱偱侾俋俇斣栚亜
丂丂丂(僀)丂仯偑A丄B 偺応崌4俹2亖侾俀捠傝 丂亙偙偙傑偱偱俀侽俉斣栚亜
丂(iv)侾俁係仯仯偺応崌
丂丂丂侾俁係侾俀丒丒丒俀侽俋斣栚
丂丂丂侾俁係侾俁丒丒丒俀侾侽斣栚
丂丂丂侾俁係侾係丒丒丒俀侾侾斣栚
丂丂丂侾俁係侾俆丒丒丒俀侾俀斣栚
丂丂丂侾俁係俀侾丒丒丒俀侾俁斣栚
丂丂丂侾俁係俀俀丒丒丒俀侾係斣栚
丂丂丂侾俁係俀俁丒丒丒俀侾俆斣栚
丂丂丂侾俁係俀係丒丒丒俀侾俇斣栚
丂丂丂侾俁係俀俆丒丒丒俀侾俈斣栚
丂丂丂侾俁係俁侾丒丒丒俀侾俉斣栚
丂丂丂侾俁係俁俀丒丒丒俀侾俋斣栚
丂丂丂侾俁係俁係丒丒丒俀俀侽斣栚
丂丂丂侾俁係俁俆丒丒丒俀俀侾斣栚
丂丂丂侾俁係係侾丒丒丒俀俀俀斣栚
傛偭偰丂俀俀俀斣栚偼丂侾俁係係侾丂偱偁傞丅
仚偪側傒偵俵傪媮傔傞偨傔偺堦棗昞仚
| 亙慖傫偱偒偨暥帤亜 | 捠傝 | 崌寁 |
|---|---|---|
| 侾丂侾丂俀丂俀丂俁丂 | 丒丒丒 俁侽 | 彫寁俋侽侽捠傝 |
| 侾丂侾丂俀丂俀丂俁丂 | 丒丒丒 俁侽 | |
| 侾丂侾丂俀丂俀丂係 | 丒丒丒 俁侽 | |
| 侾丂侾丂俀丂俀丂俆 | 丒丒丒 俁侽 | |
| 侾丂侾丂俁丂俁丂俀 | 丒丒丒 俁侽 | |
| 侾丂侾丂俁丂俁丂係 | 丒丒丒 俁侽 | |
| 侾丂侾丂俁丂俁丂俆 | 丒丒丒 俁侽 | |
| 侾丂侾丂係丂係丂俀 | 丒丒丒 俁侽 | |
| 侾丂侾丂係丂係丂俁 | 丒丒丒 俁侽 | |
| 侾丂侾丂係丂係丂俆 | 丒丒丒 俁侽 | |
| 侾丂侾丂俆丂俆丂俀 | 丒丒丒 俁侽 | |
| 侾丂侾丂俆丂俆丂俁 | 丒丒丒 俁侽 | |
| 侾丂侾丂俆丂俆丂係 | 丒丒丒 俁侽 | |
| 俀丂俀丂俁丂俁丂侾 | 丒丒丒 俁侽 | |
| 俀丂俀丂俁丂俁丂係 | 丒丒丒 俁侽 | |
| 俀丂俀丂俁丂俁丂俆 | 丒丒丒 俁侽 | |
| 俀丂俀丂係丂係丂侾 | 丒丒丒 俁侽 | |
| 俀丂俀丂係丂係丂俁 | 丒丒丒 俁侽 | |
| 俀丂俀丂係丂係丂俆 | 丒丒丒 俁侽 | |
| 俀丂俀丂俆丂俆丂侾 | 丒丒丒 俁侽 | |
| 俀丂俀丂俆丂俆丂俁 | 丒丒丒 俁侽 | |
| 俀丂俀丂俆丂俆丂係 | 丒丒丒 俁侽 | |
| 俁丂俁丂係丂係丂侾 | 丒丒丒 俁侽 | |
| 俁丂俁丂係丂係丂俀 | 丒丒丒 俁侽 | |
| 俁丂俁丂係丂係丂俆 | 丒丒丒 俁侽 | |
| 俁丂俁丂俆丂俆丂侾 | 丒丒丒 俁侽 | |
| 俁丂俁丂俆丂俆丂俀 | 丒丒丒 俁侽 | |
| 俁丂俁丂俆丂俆丂係 | 丒丒丒 俁侽 | |
| 係丂係丂俆丂俆丂侾 | 丒丒丒 俁侽 | |
| 係丂係丂俆丂俆丂俀 | 丒丒丒 俁侽 | |
| 係丂係丂俆丂俆丂俁 | 丒丒丒 俁侽 | |
| 侾丂侾丂俀丂俁丂係 | 丒丒丒 俇侽 | 彫寁侾俀侽侽捠傝 |
| 侾丂侾丂俀丂俁丂俆 | 丒丒丒 俇侽 | |
| 侾丂侾丂俀丂係丂俆 | 丒丒丒 俇侽 | |
| 侾丂侾丂俁丂係丂俆 | 丒丒丒 俇侽 | |
| 俀丂俀丂侾丂俁丂係 | 丒丒丒 俇侽 | |
| 俀丂俀丂侾丂俁丂俆 | 丒丒丒 俇侽 | |
| 俀丂俀丂侾丂係丂俆 | 丒丒丒 俇侽 | |
| 俀丂俀丂俁丂係丂俆 | 丒丒丒 俇侽 | |
| 俁丂俁丂侾丂俀丂係 | 丒丒丒 俇侽 | |
| 俁丂俁丂侾丂俀丂俆 | 丒丒丒 俇侽 | |
| 俁丂俁丂侾丂係丂俆 | 丒丒丒 俇侽 | |
| 俁丂俁丂俀丂係丂俆 | 丒丒丒 俇侽 | |
| 係丂係丂侾丂俀丂俁 | 丒丒丒 俇侽 | |
| 係丂係丂侾丂俀丂俆 | 丒丒丒 俇侽 | |
| 係丂係丂侾丂俁丂俆 | 丒丒丒 俇侽 | |
| 係丂係丂俀丂俁丂俆 | 丒丒丒 俇侽 | |
| 俆丂俆丂侾丂俀丂俁 | 丒丒丒 俇侽 | |
| 俆丂俆丂侾丂俀丂係 | 丒丒丒 俇侽 | |
| 俆丂俆丂侾丂俁丂係 | 丒丒丒 俇侽 | |
| 俆丂俆丂俀丂俁丂係 | 丒丒丒 俇侽 | |
| 侾丂俀丂俁丂係丂俆 | 丒丒丒侾俀侽 | 彫寁侾俀侽捠傝 |
| 丂 | 俵 | 崌寁俀俀俀侽捠傝 |
夝摎丒偦偺3
乮儁儞僱亅儉丗偺偭偙傫乯
乮侾乯
aabbc偺僞僀僾丂丂慖傃曽偼5俠2丒3俠1亖30捠傝丂暲傋曽偼30丒5両/乮2両丒2両乯亖900捠傝
aabcd偺僞僀僾丂丂慖傃曽偼5俠1丒4俠3亖20捠傝丂暲傋曽偼20丒5両/2両亖1200捠傝
abcde偺僞僀僾丂丂慖傃曽偼5俠0丒5俠5亖1捠傝丂暲傋曽偼1丒5両亖120捠傝
丂丂俵亖900亄1200亄120亖2220亖222丒10
乮俀乯
俵/2亖1110
1仜仜仜仜偺屄悢偼丂2220/5亖444屄
俀仜仜仜仜偺屄悢傕丂丂丂丂丂丂丂444屄丒丒丒丒椵寁888屄
俁仜仜仜仜偺屄悢傕丂丂丂丂丂丂丂444屄丒丒丒丒椵寁1332屄
傛偭偰媮傔傞悢偼丂俁仜仜仜仜
俁侾仜仜仜偺屄悢偼乮侾乯偲摨條偺寁嶼傪峴偭偰俋俇屄丒丒丒丒椵寁俋俉係屄
俁俀仜仜仜偺屄悢傕丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俋俇屄丒丒丒丒椵寁侾侽俉侽屄
俁俁仜仜仜偺屄悢偼丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俇侽屄丒丒丒丒椵寁侾侾係侽屄
傛偭偰媮傔傞悢偼丂俁俁仜仜仜
俁俁侾仜仜偺屄悢偼丂俇侽/係亖侾俆屄丒丒丒丒椵寁侾侽俋俆屄
俁俁俀仜仜偺屄悢傕丂丂丂丂丂丂侾俆屄丒丒丒丒椵寁侾侾侾侽屄
傛偭偰俁俁俀仜仜偺嵟戝悢偑摎偊偲側傞丂丂丂丂丂乮摎偊乯俁俁俀俆俆
乮俁乯
俵/俆亖444
乮俀乯偵偍偄偰丂侾仜仜仜仜偺屄悢偼444屄偩偭偨偐傜
侾仜仜仜仜偺嵟戝悢偑摎偊偲側傞丂丂丂丂丂丂丂乮摎偊乯侾俆俆係係
乮係乯
俵/10亖222
侾侾仜仜仜偺屄悢偼俁俁仜仜仜偺屄悢偲摨偠偩偐傜俇侽屄
侾俀仜仜仜偺屄悢偼俁侾仜仜仜偺屄悢偲摨偠偩偐傜俋俇屄丒丒丒丒椵寁侾俆俇屄
侾俁仜仜仜偺屄悢傕丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俋俇屄丒丒丒丒椵寁俀俆俀屄
傛偭偰媮傔傞悢偼侾俁仜仜仜
侾俁侾仜仜偺屄悢偼俁俁侾仜仜偺屄悢偲摨偠偩偐傜侾俆屄丒丒丒丒椵寁侾俈侾屄
侾俁俀仜仜偺屄悢偼乮侾乯偲摨條偺寁嶼傪峴偭偰俀俀屄丒丒丒丒椵寁侾俋俁屄
侾俁俁仜仜偺屄悢偼侾俁侾仜仜偺屄悢偲摨偠偩偐傜侾俆屄丒丒丒椵寁俀侽俉屄
侾俁係仜仜偺屄悢偼侾俁俀仜仜偺屄悢偲摨偠偩偐傜俀俀屄丒丒丒丒椵寁俀俁侽屄
傛偭偰媮傔傞悢偼侾俁係仜仜
侾俁係侾仜偺屄悢偼係屄丒丒丒丒椵寁俀侾俀屄
侾俁係俀仜偺屄悢偼俆屄丒丒丒丒椵寁俀侾俈屄
侾俁係俁仜偺屄悢偼係屄丒丒丒丒椵寁俀俀侾屄
傛偭偰侾俁係係仜偺嵟彫悢偑摎偊偲側傞丂丂丂丂丂丂乮摎偊乯侾俁係係侾
夝摎丒偦偺4
乮儁儞僱亅儉丗岼偺柌乯
乮1乯
(i)5庬椶慡偰傪巊偆応崌
5P4亖5亊4亊3亊2亖120
(ii)1庬椶偩偗摨偠悢傪
巊偆応崌
丒摨偠悢偼5庬椶
丒偦偺摨偠悢偺暲傋曽偼5C2亖5亊4/2亖10
丒偦偺懠偺3悢偼4庬椶偺拞偐傜慖傇偺偱4P3亖4亊3亊2亖24
場偭偰丄5亊10亊24亖1200
(iii)2庬椶摨偠悢傪巊偆応崌
丒摨偠悢偺慻傒崌傢偣偼5C2亖5亊4/2亖10
丒偦偺暲傋曽偼5C2亊3C2亖5亊4亊3/2亖30
丒巆傝偺悢偼3庬椶
場偭偰丄10亊30亊3亖900
埲忋偺悢傪慡晹壛偊偰丄媮傔傞悢偼120+1200+900亖2220偲側傞丅妋偐偵10偺攞悢偱偁傞丅
(2)
媮傔傞傕偺偼彫偝偄曽偐傜2220/2亖1110斣栚偱偁傞丅傎傏恀傫拞偺抣偲悇嶡偝傟傞丅
弌棃傞悢傪彂偒弌偡偲丄
1仜仜仜仜丄2仜仜仜仜丄3仜仜仜仜丄4仜仜仜仜媦傃5仜仜仜仜偵側傞偙偲偑暘偐傞丅
場偭偰丄奺乆偺悢偼2220/5亖444偯偮偁傞偲悇掕偝傟傞丅懄偪丄3仜仜仜仜偱偁傞丅
偲偙傠偱丄3仜仜仜仜偺師偺寘傪彂偔偲丄
31仜仜仜丄32仜仜仜丄33仜仜仜丄34仜仜仜媦傃35仜仜仜偱偁傝丄33仜仜仜埲奜偺奺乆偺彂偒弌偝傟傞悢抣偺悢偼摨偠偱偁傞丅
場偭偰丄33仜仜仜偺恀傫拞偵嬤偄偲暘偐傞丅
彫偝偄弴偵峫偊傞偲丄331仜仜偼1,2,24,4,5,5偺拞偐傜2悢慖傇帠偲側傝丄摨偠悢偺慻傒崌傢偣偼3捠傝丄堎側傞悢偺慻傒崌傢偣偼4P2亖4亊3亖12捠傝丄場偭偰15捠傝偱偁傞丅332仜仜丄
334仜仜丄335仜仜傕慡偔摨偠偱偁傞偺偱恀傫拞偺彫偝偄曽偺悢偼33255偱偁傞丅
(3)
媮傔傞傕偺偼彫偝偄曽偐傜2220/5亖444斣栚偱偁傞丅
偙傟偼忋婰(2)偱峫嶡偟偨傛偆偵1仜仜仜仜偺堦斣戝偒側悢偱偁傞偐傜丄帺偢偲15544偲側傞丅
(4)
媮傔傞傕偺偼彫偝偄曽偐傜2220/10亖222斣栚偱偁傞丅
偲偙傠偱丄11仜仜仜丄12仜仜仜丄13仜仜仜丄14仜仜仜媦傃15仜仜仜偱弌棃傞悢偼11仜仜仜偺傒偑彮側偔丄懠偼慡偰摨偠偱偁傞丅12仜仜仜傪峫偊傞偲丄1,2,3,3,4,4,5,5偺拞偐傜3悢傪慖傇帠偵側傞丅
丒巆傝3悢慡偰偑堎側傞悢偺慻傒崌傢偣偼丄5P3亖5亊4亊3亖60
丒巆傝3悢拞摨偠悢偑偁傞応崌偼丄3,4,5偺3庬椶偱巆傝偺悢偼4庬椶偐傜慖傇偺偱
3亊3亊4亖36偲側傞丅
場偭偰丄60+36亖96偲側傞丅偙傟偑4庬椶偁傞偺偱444-96亊4亖60偑11仜仜仜偺屄悢偱偁傞丅偙傟傜傛傝222亖60+96+66偲側傞丅懄偪丄13仜仜仜偺彫偝偄曽偐傜66斣栚偺悢偲側傞丅
13仜仜仜傪彫偝偄弴偵昞偡偲丄131仜仜丄132仜仜丄133仜仜丄134仜仜媦傃135仜仜側偺偱
133仜仜偲悇嶡偝傟傞丅
偲偙傠偱丄忋婰偲摨偠峫偊偱峫嶡偡傟偽丄131仜仜偲133仜仜偺悢偼摨偠偱丄
132仜仜丄134仜仜媦傃135仜仜傕摨偠偱偁傞丅
屻幰偺132仜仜偼丄1,2,3,4,4,5,5偐傜2悢傪慖傋偽椙偔丄
丒堎側傞悢偺応崌偼5P2亖5亊4亖20偲側傞
丒摨偠悢偼2捠傝偱偁傞丅
場偭偰丄22捠傝偑3庬椶偁傝丄131仜仜偲133仜仜偺崌寁悢偼96-22亊3亖30偲側傞丅懄偪丄
131仜仜丄132仜仜丄133仜仜偺崌寁偼52偱偁傝丄66斣栚偼134仜仜偺彫偝偄曽偐傜14斣栚偺悢偲側傞丅
1341仜偼4屄丄1342仜偼5屄丄1343仜偼4屄偱偁傞偐傜丄媮傔傞傕偺偼13441偲側傞丅
夝摎丒偦偺5
乮儁儞僱亅儉丗揮埵斀墳乯
戣堄傪枮偨偡俆寘偺惍悢偵偼丄奺寘偺悢偑慡偰堎側傞応崌丄堦慻偺摨偠悢傪娷傓応崌丄
擇慻偺摨偠悢傪娷傓応崌偺丄俁偮偺僷僞乕儞偑懚嵼偡傞丅
枩埵偑侾偺応崌丄俆寘偺惍悢偼係係係捠傝偑峫偊傜傟傞丅乮昞侾乯
椺偊偽丄侾俀仩仩仩偺応崌
丂(i)慡偰堎側傞悢傪娷傓応崌丗俁亊俀亊侾亖俇捠傝
丂(ii)堦慻偺摨偠悢傪娷傓応崌丗俆係捠傝
丂丂丂丒乽侾乿傪擇偮娷傓応崌丗俁亊俁亊俀亖侾俉捠傝
丂丂丂丒乽俀乿傪擇偮娷傓応崌丗俁亊俁亊俀亖侾俉捠傝
丂丂丂丒乽俁乿丄乽係乿傑偨偼乽俆乿傪擇偮娷傓応崌丗俁亊俁亊俀亖侾俉捠傝
丂(iii)擇慻偺摨偠悢傪娷傓応崌丗俁俇捠傝
丂丂丂丒乽侾乿偲乽俀乿傪擇偮偢偮娷傓応崌丗俁亊俀亊俁亖侾俉捠傝
丂丂丂丒乽侾乿傪堦慻丄乽俁乿丄乽係乿傑偨偼乽俆乿傪堦慻娷傓応崌丗俁亊俁亖俋捠傝
丂丂丂丒乽俀乿傪堦慻丄乽俁乿丄乽係乿傑偨偼乽俆乿傪堦慻娷傓応崌丗俁亊俁亖俋捠傝
昞侾
| 俆寘偺惍悢 | 悢偑慡偰 堎側傞 | 堦慻偺摨偠 悢傪娷傓 | 擇慻偺摨偠 悢傪娷傓 | 彫寁 | 椵寁 |
|---|---|---|---|---|---|
| 11仩仩仩 | 0 | 24 | 36 | 60 | 60 |
| 12仩仩仩 | 6 | 54 | 36 | 96 | 156 |
| 13仩仩仩 | 6 | 54 | 36 | 96 | 252 |
| 14仩仩仩 | 6 | 54 | 36 | 96 | 348 |
| 15仩仩仩 | 6 | 54 | 36 | 96 | 444 |
(1)枩埵偑俀乣俆偺応崌偵偮偄偰傕丄偦傟偧傟係係係捠傝偺惍悢偑懚嵼偡傞偺偱
丂丂丂俵=係係係亊俆=俀俀俀侽亖俀俀俀亊侾侽
侾侽偺攞悢偱偁傞丅
(2)昞俁傛傝丄侾侾係侽斣栚偺惍悢偼丄俁俁仩仩仩偱嵟戝偱偁傞偙偲偐傜俁俁俆俆係丅
傛偭偰丄俵乛俀亖侾侾侾侽斣栚偺惍悢偼丄俁俁俆俆係傛傝俁侽斣栚偵彫偝偄惍悢偲側傞丅
弴偵彂偒暲傋偰媮傔傞丄俁俁俀俆俆丅
昞俁
| 俆寘偺惍悢 | 悢偑慡偰 堎側傞 | 堦慻偺摨偠 悢傪娷傓 | 擇慻偺摨偠 悢傪娷傓 | 彫寁 | 椵寁 |
|---|---|---|---|---|---|
| 31仩仩仩 | 6 | 54 | 36 | 96 | 984 |
| 32仩仩仩 | 6 | 54 | 36 | 96 | 1080 |
| 33仩仩仩 | 0 | 24 | 36 | 60 | 1140 |
| 34仩仩仩 | 6 | 54 | 36 | 96 | 1236 |
| 35仩仩仩 | 6 | 54 | 36 | 96 | 1332 |
(俁)俵乛俆亖係係係斣栚偺悢偼丄昞侾偐傜侾俆俆係係丅
(係)昞侾傛傝丄俀俆俀斣栚偺惍悢偼丄侾俁仩仩仩偱嵟戝偱偁傞偙偲偐傜侾俁俆俆係丅
傛偭偰丄俵乛侾侽亖俀俀俀斣栚偺惍悢偼丄侾俁俆俆係傛傝俁侽斣栚偵彫偝偄惍悢偲側傞丅
弴偵彂偒暲傋偰媮傔傞偲丄侾俁係係侾丅
夝摎丒偦偺6
乮儁儞僱亅儉丗嶰妏掕婯乯
(1)
丂<1> 俆偮偺悢帤偑偡傋偰堎側傞傕偺丂5両亖120 屄 乧(#1)
丂<2> 侾慻偺摨偠悢傪娷傓傕偺 乧丂5丒4丒60亖1200 屄 乧(#2)
丂丂丒摨偠悢偼壗偐 乧 5 捠傝
丂丂丒懠偺俁悢偼壗偐 乧 4C3亖4 捠傝
丂丂丒偦傟傜偺暲傋曽 乧 5両/2亖60 捠傝
丂<3> 俀慻偺摨偠悢傪娷傓傕偺 乧 10丒3丒30亖900 屄 乧(#3)
丂丂丒摨偠悢偼壗偲壗偐 乧 5C2亖10 捠傝
丂丂丒懠偺侾偮偺悢偼壗偐 乧 3 捠傝
丂丂丒偦傟傜偺暲傋曽 乧 5両/2丒2亖30 捠傝
(#1)(#2)(#3)傛傝丆俆寘偺悢偺憤悢偼 120亄1200亄900亖2220 屄 仼10 偺攞悢丅[摎]
(2)
丂<1> 悢 1仜仜仜仜 偺憤悢偼 2220/5亖444 屄 乧(#4)
丂<2> 悢 112仜仜 偼 15 屄偁傞偐傜丆悢 11仜仜仜 偼 15丒4亖60 屄 乧 (#5)
丂<3> 悢 121仜仜丆悢 122仜仜 偼偦傟偧傟 15 屄丆悢 123仜仜 偼 22 屄偁傞偐傜丆悢 12仜仜仜 偼 15丒2亄22丒3亖96 屄 乧 (#6)
M/2亖1110亖444亄444亄96亄96亄30 偩偐傜丆1110 斣栚偺悢偺嵟忋埵偼(#4)傛傝 3丅
悢 31仜仜仜丆32仜仜仜 偼(#6)傛傝偦傟偧傟 96 屄丅傛偭偰丆嵍偐傜 2 偮栚偼 3丅
傛偭偰丆1110 斣栚偺悢偼丆33仮仮仮 偺彫偝偄曽偐傜 30 斣栚偱丆(#5)傛傝丆33255 [摎]
(3)
M/5亖444
偙傟偼丆(#4)傛傝 1仜仜仜仜 偺嵟戝悢偱丆偦傟偼丂15544 [摎]
(4)
M/10亖222亖60亄96亄66丆66亖15亄22亄15亄14 偩偐傜
222 斣栚偺悢偼 134仮仮 偺彫偝偄曽偐傜 14 斣栚偱丆偦傟偼 13441 [摎]
夝摎丒偦偺7
乮儁儞僱亅儉丗儈僀乯
(1)丂侾仜仜仜仜偺僞僀僾偺悢傪媮傔偰丄俆攞偡傟偽傛偄丅
壓偺仜仜仜偵偮偄偰丄侾亱丒俀亱偺傛偆偵暘椶偟偰悢偊傞丅
侾亱偼abc乮俁偮偺悢帤偑堎側傞乯僞僀僾
俀亱偼aab乮俀偮偺悢帤偑摨偠乯僞僀僾
丂侾侾仜仜仜丒丒丒侾亱4俹3 捠傝丄俀亱4亊3亊3 捠傝丒丒丒寁60捠傝
丂侾俀仜仜仜丒丒丒侾亱5俹3 捠傝丄俀亱3亊4亊3 捠傝丒丒丒寁96捠傝
丂侾俁仜仜仜丄侾係仜仜仜丄侾俆仜仜仜傕侾俀仜仜仜偲摨悢側偺偱丄
丂侾仜仜仜仜偺僞僀僾偺悢偼丄60亄96亊4亖444捠傝
傛偭偰丄俵亖444亊5亖2220
偙傟傛傝丄俵偼侾侽偺攞悢偱偁傞丅
(2)丂枩偺埵偑侾丄俀丄俁丄係丄俆偱偁傞傕偺偼偦傟偧傟摨悢側偺偱丄俵/2斣栚偺悢偼丄俁仜仜仜仜偵娷傑傟傞丅
偙偺偆偪丄愮偺埵偑侾丄俀丄係丄俆偱偁傞傕偺偼偦傟偧傟摨悢側偺偱丄俵/2斣栚偺悢偼丄俁俁仜仜仜偵娷傑傟傞丅
偙偺偆偪丄昐偺埵偑侾丄俀丄係丄俆偱偁傞傕偺偼偦傟偧傟摨悢側偺偱丄俵/2斣栚偺悢偼丄俁俁俀仜仜偺僞僀僾偱嵟傕戝偒偄悢偱偁傞丅
傛偭偰丄媮傔傞俆寘偺悢偼丄俁俁俀俆俆
(3)丂枩偺埵偑侾丄俀丄俁丄係丄俆偱偁傞傕偺偼偦傟偧傟摨悢側偺偱丄俵/5斣栚偺悢偼丄侾仜仜仜仜偺僞僀僾偱嵟傕戝偒偄悢偱偁傞丅傛偭偰丄媮傔傞俆寘偺悢偼丄侾俆俆係係
(4)丂枩偺埵偑侾丄俀丄俁丄係丄俆偱偁傞傕偺偼偦傟偧傟摨悢側偺偱丄俵/10亖222斣栚偺悢偼丄侾仜仜仜仜偺僞僀僾偵娷傑傟傞丅
(1)偺寁嶼寢壥傛傝丄
丂侾侾仜仜仜丒丒丒60捠傝
丂侾俀仜仜仜丒丒丒96捠傝
傑偨丄壓偺仜仜偱丄俁亱傪ab 僞僀僾丄係亱傪aa 僞僀僾偲偟偰
丂侾俁侾仜仜丒丒丒俁亱4亊3捠傝丄係亱3捠傝丒丒丒崌寁15捠傝
丂侾俁俀仜仜丒丒丒俁亱5亊4捠傝丄係亱2捠傝丒丒丒崌寁22捠傝
丂侾俁俁仜仜丒丒丒侾俁侾仜仜偲摨偠偱丄15捠傝
丂侾俁係侾仜丒丒丒4捠傝丄侾俁係俀仜丒丒丒5捠傝丄侾俁係俁仜丒丒丒4捠傝
埲忋偱丄60亄96亄15亄22亄15亄4亄5亄4亖221屄
偡側傢偪丄222斣栚偺悢偼丄侾俁係係仜偺堦斣彫偝偄悢偱偁傞丅
偟偨偑偭偰丄媮傔傞悢偼侾俁係係侾
夝摎丒偦偺8
乮儁儞僱亅儉丗柪巕偺梇擫乯
栤戣(1)
摨偠悢帤偺僇乕僪偼俀枃偟偐側偄偺偱丄俆枃偺僇乕僪偺慻傒崌傢偣偼丄
壓婰偺偄偢傟偐偱偁傞丅
乮偁乯俀枃亅俀枃亅侾枃丄摨偠悢帤偺僇乕僪偺慻偑俀慻偲丄扨撈偺悢帤僇乕僪侾枃
乮偄乯俀枃亅侾枃亅侾枃亅侾枃丄摨偠悢帤偺僇乕僪偺慻偑侾慻偲丄扨撈偺悢帤僇乕僪俁枃
乮偆乯侾枃亅侾枃亅侾枃亅侾枃亅侾枃丄摨偠悢帤偺僇乕僪偺慻偑侽慻偲丄扨撈偺悢帤僇乕僪俆枃
乮偁乯偺応崌
丂丂儁傾偺僇乕僪偺慻偺慖傃曽乮俆亊係亐俀乯捠傝
丂丂扨撈偺悢帤僇乕僪偺慖傃曽乮俁乯捠傝
丂丂嵍偐傜塃傊偺暲傋曽乮俆亊係亊俁亊俀亊侾亐俀亐俀乯捠傝
丂丂崌寁俋侽侽捠傝
乮偄乯偺応崌
丂丂儁傾偺僇乕僪偺慻偺慖傃曽乮俆乯捠傝
丂丂扨撈偺悢帤僇乕僪偺慖傃曽乮係亊俁亊俀亐俁亐俀乯捠傝
丂丂嵍偐傜塃傊偺暲傋曽乮俆亊係亊俁亊俀亊侾亐俀乯捠傝
丂丂崌寁侾俀侽侽捠傝
乮偆乯偺応崌
丂丂儁傾悢帤偺僇乕僪偺慻偺慖傃曽乮侾乯捠傝
丂丂扨撈偺悢帤僇乕僪偺慖傃曽乮侾乯捠傝
丂丂嵍偐傜塃傊偺暲傋曽乮俆亊係亊俁亊俀亊侾乯捠傝
丂丂崌寁侾俀侽捠傝
乮偁乯乣乮偆乯偺崌寁丂俀俀俀侽捠傝乮枛旜偑侽側偺偱侾侽偺攞悢乯
栤戣(2)
丂丂俵捠傝偺悢偺偆偪丄愭摢偑[侾][俀][俁][係][俆]偺悢帤偼摨悢偢偮偁傞丅
丂丂俵/5斣栚偺悢偼丄愭摢偑[俁]偱偁傞悢帤偺偆偪拞娫偺悢丄
丂丂傛偭偰愭摢俀寘偼俁俁丄俁寘栚偼[俀]偱偁傞悢帤偺偆偪嵟戝偺悢丄傛偭偰俁俁俀俆俆
栤戣(3)
丂丂俵/5斣栚偺悢偼丄愭摢偑[侾]偱偁傞悢帤偺偆偪嵟戝偺悢丄傛偭偰侾俆俆係係
栤戣(4)
丂丂俵/10斣栚偺悢偼丄愭摢偑[侾]偱偁傞悢帤乮係係係捠傝乯偺偆偪偺偄偢傟偐丅
摨偠悢帤偺僇乕僪偼2枃偟偐側偄偺偱丄巆傝俁枃偺僇乕僪偺慻傒崌傢偣偼丄壓婰偺偄偢傟偐偱偁傞丅
乮偊乯俀枃亅俀枃亅侾枃丄儁傾偺僇乕僪偺慻偑侾慻偲丄扨撈偺悢帤僇乕僪侾枃
乮偍乯俀枃亅侾枃亅侾枃亅侾枃丄儁傾偺僇乕僪偺慻偑侽慻偲丄扨撈偺悢帤僇乕僪俁枃
愭摢偑侾俆丄侾係丄侾俁丄侾俀偺悢偺応崌丗俋俇捠傝亊係亖俁俉係捠傝
丂丂愭摢偑侾俀偱偁傞応崌丄巆傝偺僇乕僪偼侾俀俁俁係係俆俆偱偁傞偺偱丄
丂丂乮偊乯偺応崌
丂丂丂丂儁傾偺僇乕僪偺慻偺慖傃曽乮俁乯捠傝丗乮俁俁丆係係丆俆俆偺偆偪偺丄偄偢傟偐乯
丂丂丂丂扨撈偺悢帤僇乕僪偺慖傃曽乮係乯捠傝丗乮俆俆傪慖傫偩傜巆傝偼侾俀俁係偺丄偄偢傟偐乯
丂丂丂丂嵍偐傜塃傊偺暲傋曽乮俁乯捠傝
丂丂丂丂崌寁俁俇捠傝
丂丂乮偍乯偺応崌
丂丂丂丂儁傾偺僇乕僪偺慻偺慖傃曽乮侾乯捠傝
丂丂丂丂扨撈偺悢帤僇乕僪偺慖傃曽乮俆亊係亊俁亐俁亐俀乯亖乮侾侽乯捠傝
丂丂丂丂嵍偐傜塃傊偺暲傋曽乮俁亊俀亊侾乯亖乮俇乯捠傝
丂丂丂丂崌寁俇侽捠傝
愭摢偑侾侾偺悢丗俇侽捠傝
愭摢偑侾侾偱偁傞応崌丄巆傝偺僇乕僪偼俀俀俁俁係係俆俆偱偁傞偺偱丄
丂丂乮偊乯偺応崌
丂丂丂丂儁傾偺僇乕僪偺慻偺慖
傃曽乮係乯捠傝丗乮俀俀丄俁俁丆係係丆俆俆偺偆偪偺丄偄偢傟偐乯
丂丂丂丂扨撈偺悢帤僇乕僪偺慖傃曽乮俁乯捠傝丗乮俆俆傪慖傫偩傜巆傝偼俀俁係偺丄偄偢傟偐乯
丂丂丂丂嵍偐傜塃傊偺暲傋曽乮俁乯捠傝
丂丂丂丂崌寁俁俇捠傝
丂丂乮偍乯偺応崌
丂丂丂丂儁傾偺僇乕僪偺慻偺慖傃曽乮侾乯捠傝
丂丂丂丂扨撈偺悢帤僇乕僪偺慖傃曽乮係亊俁亊俀亐俁亐俀乯亖乮係乯捠傝
丂丂丂丂嵍偐傜塃傊偺暲傋曽乮俁亊俀亊侾乯亖乮俇乯捠傝
丂丂丂丂崌寁俀係捠傝
丂丂俵/10斣栚乮俀俀俀斣栚乯偺悢偼丄
丂丂丂愭摢偑侾侾偺悢丗俇侽捠傝
丂丂丂愭摢偑侾俀偺悢丗俋俇捠傝乮椵寁侾俆俇捠傝乯
丂丂丂愭摢偑侾俁偺悢丗俋俇捠傝乮椵寁俀俆俀捠傝乯
丂丂摨條偵丄愭摢偑侾俁侾偺悢丗侾俆捠傝乮椵寁侾俈侾捠傝乯
丂丂丂丂丂丂愭摢偑侾俁俀偺悢丗俀俀捠傝乮椵寁侾俋俁捠傝乯
丂丂丂丂丂丂愭摢偑侾俁俁偺悢丗侾俆捠傝乮椵寁俀侽俉捠傝乯
丂丂丂丂丂丂愭摢偑侾俁係偺悢丗俀俀捠傝乮椵寁俀俁侽捠傝乯
丂丂丂丂丂丂愭摢偑侾俁俆偺悢丗俀俀捠傝乮椵寁俀俆俀捠傝乯
丂丂愭摢偑侾俁係偺悢偼丄埲壓偺俀俀屄丅
丂丂丂丂侾俁係侾俀乮俀侽俋斣栚乯
丂丂丂丂侾俁係侾俁乮俀侾侽斣栚乯
丂丂丂丂侾俁係侾係乮俀侾侾斣栚乯
丂丂丂丂侾俁係侾俆乮俀侾俀斣栚乯
丂丂丂丂侾俁係俀侾乮俀侾俁斣栚乯
丂丂丂丂侾俁係俀俀乮俀侾係斣栚乯
丂丂丂丂侾俁係俀俁乮俀侾俆斣栚乯
丂丂丂丂侾俁係俀係乮俀侾俇斣栚乯
丂丂丂丂侾俁係俀俆乮俀侾俈斣栚乯
丂丂丂丂侾俁係俁侾乮俀侾俉斣栚乯
丂丂丂丂侾俁係俁俀乮俀侾俋斣栚乯
丂丂丂丂侾俁係俁係乮俀俀侽斣栚乯
丂丂丂丂侾俁係俁俆乮俀俀侾斣栚乯
丂丂丂丂侾俁係係侾乮俀俀俀斣栚乯
丂丂丂丂侾俁係係俀乮俀俀俁斣栚乯
丂丂丂丂侾俁係係俁乮俀俀係斣栚乯
丂丂丂丂侾俁係係俆乮俀俀俆斣栚乯
丂丂丂丂侾俁係俆侾乮俀俀俇斣栚乯
丂丂丂丂侾俁係俆俀乮俀俀俈斣栚乯
丂丂丂丂侾俁係俆俁乮俀俀俉斣栚乯
丂丂丂丂侾俁係俆係乮俀俀俋斣栚乯
丂丂丂丂侾俁係俆俆乮俀俁侽斣栚乯
丂丂俵/10斣栚乮俀俀俀斣栚乯偺悢偼丄侾俁係係侾丅
夝摎丒偦偺9
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
(1)
5!=120
5C1*4C3*5!/2!=1200
5C2*3C1*5!/2!2!=900
崌寁亖2220 偲側傝丄10偺攞悢侓
(2)
M/2 偼丄1,2,3,4,5 偐傜丄愭摢偼3
31,32,33,34,35 偐傜丄33偱偁傝丄丄丄
331,332,334,335 偐傜丄332丒丒偺抜偺嵟戝偺悢偩偐傜丄丄丄33255
(3)
M/5 斣栚偲偄偆偙偲偼丄
愭摢偺悢偼丄1乣5側偺偱丄偦傟偧傟丄M/5 偙偢偮偁傞偼偢偩偐傜丄
愭摢偑1偺堦斣戝偒偄悢偺偼偢亖15544
(4)
M/10 偼丄1丒丒丒丒偺抜偺拞(M/5)偺敿暘(M/5)/2 偩偐傜丄丄丄
11,12,13,14,15 偩偑丄11丒丒丒偼丄
4C3*3!+4C1*3C2*
3!/2!=24+36=60 偩偑丄丄丄
12,13,14,15 偼丄(2220/5-60)/4=96 側偺偱丄
2220/10=222
60+96*2=252
252-222=30
偮傑傝丄13554 偺30屄慜偺悢丅
13554,
13553,13552,13551,13545,13544,13543,13542,13541,13535,13534,
13532,13531,13525,13524,13523,13522,13521,13515,13514,13513,
13512,13455,13454,13453,13452,13451,13445,13443,13442,13441,13435,
偐傜丄13441
夝摎丒偦偺10
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
傑偢丄偙傟傜偺悢偑偄偔偮偁傞偐傪挷傋傑偡丅
偦偺侾
丒奺埵偺悢帤偑偡傋偰堎側傞傕偺偼丄5俹5亖侾俀侽 捠傝
丒摨偠悢帤偑侾慻偁傞傕偺偼丄5俠1亊4俠3亊俆両乛俀両亖侾俀侽侽 捠傝
丂乮摨偠悢帤偺慖傃曽丄巆傝俁悢偺慖傃曽丄摨偠傕偺傪娷傓弴楍乯
丒摨偠悢帤偑俀慻偁傞傕偺偼丄5俠2亊3俠1亊俆両乛乮俀両亊俀両乯亖俋侽侽 捠傝
丂乮摨偠悢帤偺慖傃曽丄巆傝侾悢偺慖傃曽丄摨偠傕偺傪娷傓弴楍乯
偺寁 俵亖俀俀俀侽 捠傝偱偡丅
偦偺俀
暿偺峫偊偱妋擣偟偰傒傑偡丅
 仠枩偺埵偑丄侾偺偲偒
仠枩偺埵偑丄侾偺偲偒
乮偁乯枩偲愮偺埵偑摨偠悢帤偺偲偒
丒巆傝偺俁悢帤偑堎側傞傕偺偼丄4俹3亖俀係 捠傝
丒巆傝偵摨偠悢帤偑偁傞傕偺偼丄4俠1亊3俠1亊俁両乛俀両亖俁俇 捠傝
丂乮摨偠悢帤偺慖傃曽丄傕偆侾偮偺悢帤偺慖傃曽丄摨偠傕偺傪娷傓弴楍乯
偺寁 俇侽 捠傝
乮偄乯枩偲愮偺埵偺悢帤偑侾丆俀偺偲偒
丒偡傋偰偺埵偺悢帤偑堎側傞傕偺偼丄3俹3亖俇 捠傝
丒巆傝偵 侾丆俀 埲奜偱丄摨偠悢帤偺慻偑偁傞傕偺偼丄3俠1亊2俠1亊俁両乛俀両亖侾俉 捠傝
丂乮摨偠悢帤偺慖傃曽丄巆傝偺悢帤偺慖傃曽丄摨偠傕偺傪娷傓弴楍乯
丒巆傝俁悢偵丄侾偐俀偺偳偪傜偐堦曽偩偗傪娷傒丄懠偼悢帤偑堎側傞傕偺偼丄俀亊3俠2亊3俹3亖俁俇 捠傝
丂乮応崌偑俀捠傝丄懠偺悢帤偺慖傃曽丄弴楍乯
丒巆傝俁悢偵 侾偐俀偺偳偪傜偐堦曽偩偗傪娷傒丄傕偆1慻摨偠悢帤偺慻偑偁傞傕偺偼丄俀亊3俠1亊俁両乛俀両亖侾俉 捠傝
丂乮応崌偑俀捠傝丄摨偠悢帤偺慖傃曽丄摨偠傕偺傪娷傓弴楍乯
丒巆傝俁悢偵 侾偲俀 偺椉曽傪娷傓応崌丄3俠1亊3俹3亖侾俉 捠傝
丂乮巆傝偺悢帤偺慖傃曽丄俁悢帤偺暲傃曽乯
偺寁 俋俇 捠傝
乮偆乯乣乮偍乯偼丄乮偄乯偲摨偠峫偊曽側偺偱丄乮偁乯乣乮偍乯偺崌寁偼丄俇侽亄係亊俋俇亖係係係 捠傝
仠偡傋偰偺応崌偼丄俵亖俆亊係係係亖俀俀俀侽 捠傝
仸丂枩偲愮偺埵偺悢帤偑摨偠偲偒偼丄応崌偺悢偑俇侽捠傝偱丄堎側傞偲偒偼俋俇捠傝偱拲堄偑昁梫偱偡丅
乮侾乯
俵亖俀俀俀侽 側偺偱侾侽偺攞悢偱偡丅
乮俀乯
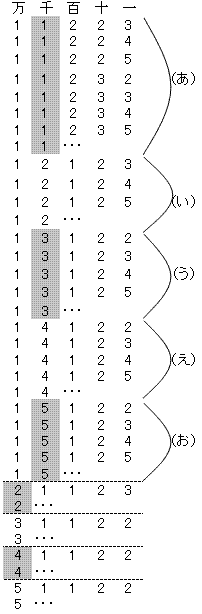
俵乛俀 斣栚偺悢偼丄嵟彫偲嵟戝偺暯嬒抣乮33333乯傛傝彫偝側嵟戝偺悢偱偡丅
| 彫偝偄弴偵暲傋偨悢 | 丂 | 戝偒偄弴偵暲傋偨悢 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 枩 | 愮 | 昐 | 廫 | 堦 | 丂 | 枩 | 愮 | 昐 | 廫 | 堦 |
| 1 | 1 | 2 | 2 | 3 | 丂 | 5 | 5 | 4 | 4 | 3 |
| 1 | 1 | 2 | 2 | 4 | 丂 | 5 | 5 | 4 | 4 | 2 |
| 1 | 1 | 2 | 2 | 5 | 丂 | 5 | 5 | 4 | 4 | 1 |
| 1 | 1 | 2 | 3 | 2 | 丂 | 5 | 5 | 4 | 3 | 4 |
| 丒丒丒 | 丂 | 丒丒丒 | ||||||||
嵍塃傪尒斾傋傞偲丄摨偠埵偺悢帤偺崌寁偑俇偵側傞傛偆側懳偵側傝傑偡丅
偩偐傜丄媮傔傞悢偼丄俁俁俀俆俆 偱偡丅
乮俁乯
俵乛俆 斣栚偺悢偼丄枩偺埵偑侾偱巒傑傞嵟戝偺悢偱偡丅
偩偐傜丄侾俆俆係係偱偡丅
乮係乯
俵乛侾侽 斣栚偺悢偼丄枩偺埵偑侾偱巒傑傞悢偺拞墰晅嬤偺悢偱偡丅
姶妎揑偵偼乮俀乯偺偲偒偺傛偆偵丄侾俁俁俀俆 偲摎偊偨偔側傝傑偡偑丄
偙傟偼俵乛侾侽亖俀俀俀斣栚偱偼偁傝傑偣傫丅
俇侽亄俋俇亄侾亖侾俆俈斣栚偑丄侾俁侾俀俀偱偡丅
13??? 偲側偭偰偄傞俋俇屄偺悢傪挷傋傞偲丄
|
|
|
|
夝摎丒偦偺11
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮侾乯俀俀俀侽捠傝丂乮俀乯俁俁俀俆俆丂乮俁乯侾俆俆係係丂乮係乯侾俁係係侾
(1) 俆枃偺僇乕僪偱嶌傞俆寘偺悢帤偺慻傒崌傢偣偼丂
俙俙俛俛俠俠俢俢俤俤偲偡傞偲師偺俁僷僞乕儞偵暘偗傜傟傑偡丅
侾亱俙俛俠俢俤丂丂俀亱俙俙俛俠俢丂丂俁亱俙俙俛俛俠丂偺俁庬椶偱偡丅
侾亱偺慻傒崌傢偣偼俆亊係亊俁亊俀亊侾亖侾俀侽捠傝
俀亱偺慻傒崌傢偣偼俙乣俤傑偱摨偠悢帤傪娷傓偺偼俆捠傝
偦偟偰慖偽傟偨悢帤偺偳傟傪巊偆偐尒傞偲係庬椶偁傝傑偡丅偦偺暲傃懼偊偼師偺捠傝偱偡丅
丂俆亊係亊乮俆亊係亊俁亊俀亊侾乯/俀亊侾亖侾俀侽侽捠傝
俁亱偺慻傒崌傢偣偼俙乣俤偲俙乣俤傑偱偺悢帤俀屄偯偮娷傓悢帤偼丄師偺侾侽捠傝偱偡丅
丂俙俙俛俛丆俙俙俠俠丄俙俙俢俢丆俙俙俤俤丆俛俛俠俠丆
丂俛俛俢俢丆俛俛俤俤丆俠俠俢俢丏俠俠俤俤丏俢俢俤俤丏
偦傟偧傟偵俁偮偺慻傒崌傢偣偑偁傝傑偡丅廬偭偰侾侽亊俁亖俁侽捠傝
偙傟偺慻傒崌傢偣偼師偺捠傝偱偡丅
丂侾侽亊俁亊乮俆亊係亊俁亊俀亊侾乯/乮俀亊侾乯亊乮俀亊侾乯亖俋侽侽捠傝
崌寁丂丂
侾亱亄俀亱亄俁亱亖侾俀侽亄侾俀侽侽亄俋侽侽亖俀俀俀侽捠傝偱偡丅
乮俀乯
M/2偺夝摎仺俁俁俁俁俁俁偵嬤偄彫偝偄曽偐傜偺嵟戝偺悢帤側偺偱俁俁俀俆俆偱偁傞帠偑暘偐傝傑偡丅
乮俁乯
M/5偺夝摎仺侾媦傃俀媦傃俁媦傃係媦傃俆偐傜巒傑傞俆寘偺悢帤偼摨悢側偺偱
侾偐傜巒傑傞彫偝偄曽偐傜偺悢帤偱嵟戝偺傕偺偲暘偐傝侾俆俆係係偱偡丅
乮係乯
M/10偺夝摎仺侾侾俀俀俁乣俆俆係係俁傑偱俀俀俀侽屄偺悢帤偑偁傝傑偡丅
摢偑侾丄俀丆俁丆係丆俆偲側傞悢帤偼摨悢偱偡丅444屄偁傝傑偡丅
廬偭偰M/10偼444/2=222斣栚偼侾偐傜巒傑傞5寘偺悢帤偺壓4寘偑侾俀俀俁偐傜
俆俆係係傑偱偺2暘偺侾乮拞娫乯側偺偱僄僋僙儖偱壓恾偺捠傝悢偊偰尒傑偟偨丅
偦偺寢壥222斣栚偼侾俁係係侾偲暘偐傝傑偟偨丅

夝摎丒偦偺12
乮儁儞僱亅儉丗teki乯
侾丂俆寘偺悢帤傪嶌傞応崌丄
丂丂乮侾乯丂俆偮偲傕悢帤偑堘偆応崌丄俆両亖侾俀侽捠傝
丂丂乮俀乯丂侾慻偩偗摨堦悢帤偺応崌丄俆亊係亊俆両亐俀亖侾俀侽侽捠傝
丂丂乮俁乯丂俀慻偺摨堦悢帤偑偁傞応崌丄侾侽亊俁亊俆両亐係亖俋侽侽捠傝
崌寁丄俀俀俀侽捠傝偱丄侾侽偺攞悢偱偡丅
嵟弶偺俆偲侾侽偼丄5C1偲5C2丄
師偺係偲俁偼丄4C1偲3C2丄嵟屻偺俀偲係偼丄
俀両媦傃俀両亊俀両偱偡丅乮愢柧偼徣棯偟傑偡丅乯
偄偢傟偵偣傛丄偙偺忦審偱俆寘偺悢傪嶌傞曽朄偼丄俁侽偺攞悢偲偄偊傑偡丅
俀丂俁俁俀俆俆
偙偺忦審偱偱偒傞嵟戝悢偲嵟彫悢偺榓丄俀斣栚偵戝偒偄悢偲俀斣栚偵彫偝偄
悢偺榓丒丒丒丒丒丒丒丒丂偼忢偵俇俇俇俇俇偱偡丅乮僈僂僗偺懌偟嶼偺梫椞乯
偮傑傝丄嶌傟傞悢偺暯嬒偼丄俁俁俁俁俁偱偡偺偱丄戣堄偺悢偼偙傟偵嵟傕嬤偄
俁俁俁俁俁傪挻偊側偄悢偲尵偊傑偡丅
俁丂侾俆俆係係
嶌傟傞悢偺侾枩丄愮丄昐丄廫丄堦偺埵偵偼丄侾乣俆偑嬒摍偵尰傟傑偡丅
傛偭偰丄戣堄偺悢偼丄尵偄姺偊傟偽丄乽侾枩偺埵偑侾偺嵟戝悢乿偲偄偆
偙偲偵側傝傑偡丅
係丂侾俁係係侾
偆傑偄曽朄偑尒偮偐傜偢丄寢嬊俀俀俀斣栚傑偱丄暲傋傑偟偨丅乮暲傋懝偹
偰側偄偙偲傪婩傞偩偗偱偡(^^;;乯
惓夝幰
| 偺偭偙傫 | 栭傆偐偟偺偮傜偄偍偠偝傫 | 柪巕偺梇擫 |
| 岼偺柌 | teki | 挿嶈搰尨丂偐偑傒 |
| 揮埵斀墳 | 昹揷丂柧枻 | 僗儌乕僋儅儞 |
| 忨偺偍偠偝傫 | 儈僀 | 嶰妏掕婯 |
僐儊儞僩
奆偝傫丄偍朲偟偄帪婜側偺偐丄栤戣偑擄偟偐偭偨偺偱偟傚偆偐丄
夝摎傪偍婑偣偄偨偩偄偨曽偑彮側偄寧偱偟偨丅
(2)偼丄俵捠傝偺俆寘偺惍悢偺偆偪丄敿悢偼俁俁俁俁俁傛傝彫偝偔丄
敿悢偼俁俁俁俁俁傛傝戝偒偄偲偄偆偙偲偐傜丄媮傔傞偙偲偑偱偒傑偡丅
(3)偼丄愭摢偺悢偑丄侾丆俀丆俁丆係丆俆偵側傞俆寘偺惍悢偼丄摨悢偁傞偲偄偆
懳徧惈偐傜媮傔傞偙偲偑偱偒傑偡丅
(4)偼丄挌擩偵悢偊傞偟偐側偝偦偆偱偡丅
 top
top