142.9進数のかけ算
9進数で表された5数8888、8887、8886、8885、8884の積
8888×8887×8886×8885×8884
を9進法で表したときの下4桁を求めよ。
問題の出典
広中杯ハイレベル中学数学に挑戦
算数オリンピック委員会監修
講談社ブルーバックス
2006年トライヤル問題
答えと解説
解答・その1
(ペンネ-ム:のっこん)
9進法用のかけ算九九表を作る
2・5=11、2・6=13、2・7=15、2・8=17
3・3=10、3・4=13、3・5=16、3・6=20、3・7=23、3・8=26
4・3=13、4・4=17、4・5=22、4・6=26、4・7=31、4・8=35
5・2=11、5・3=16、5・4=22、5・5=27、5・6=33、5・7=38、5・8=44
6・2=13、6・3=20、6・4=26、6・5=33、6・6=40、6・7=46、6・8=53
7・2=15、7・3=23、7・4=31、7・5=38、7・6=46、7・7=54、7・8=62
8・2=17、8・3=26、8・4=35、8・5=44、8・6=53、8・7=62、8・8=71
表に従い、かけ算を行う
(下4桁が求められているので、下4桁に関係する計算のみ行う)
1)8888×8887=8888×7+8888×80+8888×800+8888×8000
→8882+8810+8100+1000→0002
2)8886×2→8883
3)8883×8885=8883×5+8883×80+8883×800+8883×8000
→8856+8360+3600+6000→0026
4)8884×26=8884×6+8884×20→8856+8780→8746
(答)8746
解答・その2
(ペンネ-ム:赤影)
基本は力ずくで愚直に計算することだと思われるが、計算量を減らす工夫を考える。
真ん中の8886=nと置くと、
与式=(n-2)(n-1)n(n+1)(n+2)
となるから、因数分解の公式を使って
与式=n(n+1)(n-1)(n+2)(n-2)
=n(n2-1)(n2-4)・・・・・(1)
これならば、n2を計算すれば、3つの数の積ですむのでまともに5数の積を計算するよりは良さそうだし、計算誤りのリスクも少ないと思われる。
さて、n=8886であるから、
n2を計算する。
愚直に筆算すると、
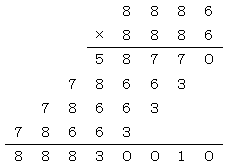
より、n2=8886×8886=88830010となる。
ゆえに、
(1)の第2項=88830010-1=888830008
(1)の第3項=88830010-4=888830005 となる。
そこで、まず①の第2項と第3項の積を求める。
最終的に求めるのは下4桁だから、上記筆算のやり方を見れば、それぞれの下4桁の積を求めれば十分である。
第2項(下4桁)×第3項(下4桁)=0008×0005=8×5=44
よって、(1)の下4桁=8886×44の下4桁=438746の下4桁=8746。
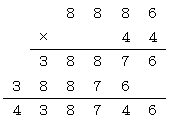
以上より、求める答えは8746
ちなみに、計算順序を第1項×第2項を先にして、後から第3項をかけても同様の結果を得たから、上記答えは正しいと思う。
解答・その3
(ペンネ-ム:オヤジ)
| 8888×8887×8886×8885×8884 (9) | |
| = | (10000-1)×(10000-2)×(10000-3)×(10000-4)×(10000-5) (9) |
| = | (10000)5-16×(10000)4+104×(10000)3 -270×(10000)2+334×10000-143 (9) |
| = | 100000104000003340000 |
| -) 160000027000000143 | |
| = | 88730103862003338746 (9) |
∴ 8746
解答・その4
(ペンネ-ム:長崎島原 かがみ)
8888(9)
=8×93+8×92+8×91+8(10)
=5832+648+72+8 (10)
=6560(10)
となるので
∴8887(9)=6560-1=6559(10)
∴8886(9)=6560-2=6558(10)
∴8885(9)=6560-3=6557(10)
∴8884(9)=6560-4=6556(10)
だから
8888×8887×8886×8885×8884(9)
=6560×6559×6558×6557×6556(10)
=12129894153051037440(10)
=88730103862003338746(9) ※下記の<割り算>による
したがって、下4桁は 8746 になります。
割り算

解答・その5
(ペンネ-ム:巷の夢)
9進数の8886をAとすると、
8888×8887×8886×8885×8884=(A+2)(A+1)A(A-1)(A-2)=(A2-4)(A2-1)A
これより下4桁は4×Aにしか表れないので、A=8×93+8×92+8×9+6に注意して4×Aの計算を行い9の累乗に注意して表すと、
8×93+7×92+4×9+6となる。
因って、求めるものは8746である。
この後、じっくり考えていたら、8888の次は9進法で10000である事に気付き、問題の数は各々1~5を引いたものだからと分かりました。うーんー、上手に問題を作ってありますね。しかし、こんな問題を中学生が短時間で解いてしまうのですか・・・・?小職など何時間も考えてやっと辿り着いたのに・・・・、やはり才能の差というものは認めざるを得ませんね。脱帽です。
先ほどの計算が正に色褪せて・・・・・。
8888×8887×8886×8885×8884=(10000-1)(10000-2)(10000-3)(10000-4)(10000-5)
であるから9進法の下4桁は10000-1×2×3×4×5であるから、9進法で表して、
8888+1-143=8746となる。
解答・その6
(ペンネ-ム:転位反応)
9進数を10進数に変換して計算し、その結果を9進数に変換する。
| 8888(9) | =8×9+8×92+8×91+8×90 |
| =(9-1)×93+(9-1)×92+(9-1)×91+(9-1)×1 | |
| =94-1 |
よって、10進数に変換した5数の積は、次式で与えられる。
| (94-1)(94-2)(94-3)(94-4)(94-5) | |
| = | 94(916-15×912+37×98+15×94+274)-120 |
| = | 94(916-15×912+37×98+15×94+273)+94-120 |
| = | 94(916-15×912+37×98+15×94+273)+6441 |
これを9進数に変換すれば良いが、第一項は、9で4回割りきれるので、 第二項についてのみ考えれば良い。
6441÷9=715 余り6
715÷9= 79 余り4
79÷9= 8 余り7
8÷9= 0 余り8
よって、下4桁は、8746
解答・その7
 (ペンネ-ム:杖のおじさん)
(ペンネ-ム:杖のおじさん)
答えは8746です、
8888×8887×8886×8885×8884
8889=10000なので8888=10000-1となるので下記のようにして考えました。
10000Nー1×2×3×4×5(Nは正の整数)
上記のを9進法で下記のように計算します。
矢印の左が10進法で右が9進法に変換した数字です。
1×2= 2→ 2・・・(1)
3×4=12→13・・・(2)
5→5・・・(3)
(1) ×(2)=2×13=26→26・・・(4)
(3)×(4)=5×26=5×6+5×2×10=130=30+100
9進法に変換→33+110=143・・・(5)
10000=8889なので次の式になります。
8889-143=8746が答えです。
解答・その8
(ペンネ-ム:スモークマン)
8888=10000-1
8887=10000-2
8886=10000-3
8885=10000-4
8884=10000-5
8888*8887*8886*8885=(10000-1)(10000-2)(10000-3)(10000-4)(10000-5)
の下4桁は、0000-5! になるから、、、
120=92+4*9+3 だから、
0000-143=8746 (9進法)
でいいのかな ^^
解答・その9
(ペンネ-ム:こまったコ)
9進法なので 88888+1=100000 になる。
これを応用すると問題の式は
(10000-1) (10000-2) (10000-3) (10000-4) (10000-5) になる。
10000 = A とすると
(A-1) (A-2) (A-3) (A-4) (A-5) = a5 -16a4 +14a3 -270a2 +334a -143
+334a -143 の部分だけで 33388746
上の部分を計算しても下4桁に影響はない。
よって答えは 8746
解答・その10
(ペンネ-ム:ぐりま)
A=94 とすると、
8888(9)=A-1、8887(9)=A-2、8886(9)=A-3、8885(9)=A-4、8884(9)=A-5
P =8888(9)・8887(9)・8886(9)・8885(9)・8884(9)
=(A-1)(A-2)(A-3)(A-4)(A-5)
=A5-15A4+85A3-225A2+274A-120
ここで、係数は10進数です。
また、9=a とおくと、A=a4だから、
P = a20-15a16+85a12-225a8+274a4-120
=8a19+(93-15) a16+84a12+(94-225)a8+273a4+(94-120)
ここで、下線部分は9進表示すると下4桁は0となるので、求める下4桁は
94-120 を9進表示したものとなります。
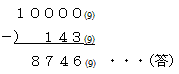
考察
P = a20-15a16+85a12-225a8+274a4-120
=( a16-15a12+85a8-225a4+273)a4+(94-120)
とすれば、下線部≧0は自明だから、この変形で十分かな?
解答・その11
(ペンネ-ム:三角定規)
以下、数値はすべて9進法で表記します。
《解》
8888=104-1、~、8884=104-5 ・・・(1)
であるから、
8888×8887×8886×8885×8884
=(104-1) (104-2) (104-3) (104-4) (104-5) ・・・(2)
(2)の下4けたは、(2)を104で割った余りに他ならない。また、
104-1≡-1 (mod 104) ・・・(3)
だから、
(104-1) (104-2)≡-1・(104-2)=104+2≡2
(mod 104) ・・・(4)
これらを繰り返し用いると、
(104-1) (104-2) (104-3) (104-4) (104-5)
≡(-1) (-2) (-3) (-4) (-5)≡-143≡8746 (mod 104)
[答] 8746
解答・その12
(ペンネ-ム:バルタン星人)
答え
8746
プロセス
8888×8887×8886×8885×8884=
(10000-1)(10000-2)(10000-3)(10000-4)(10000-5)
10000の項は下4桁は0になるので10000-10進法表記の120を計算すれば良い
120=81+4×9+3=9進法で143
9進法で筆算計算
10000
- 143
=8746
解答・その13
(ペンネ-ム:ミイ)
<9>は9進法、<10>は10進法の数
8888<9>=10000-1 <9>
8887<9>=10000-2 <9>
8886<9>=10000-3 <9>
8885<9>=10000-4 <9>
8884<9>=10000-5 <9>
これらをすべてかけあわせると
(10000n-1×2×3×4×5) <9> (nは自然数)・・・(1)
となる。ここで
1×2×3×4×5 <9>
=1×2×3×4×5 <10>
=120 <10>
=1×81+4×9+3 <10>
=143 <9>
であるから、(1)は
10000(n-1)+10000-143 <9>
=10000(n-1)+8746 <9>
よって、下4桁は 8746
解答・その14
(ペンネ-ム:迷子の雄猫)
答 8746
8888×8887×8886×8885×8884
= (10000-1)×(10000-2)×(10000-3)×(10000-4)×(10000-5)
9進数で表された5数の下4桁(aとする)を求めるのだから、10000との積は無視して
いい。
a = (10000 - 1×2×3×4×5) ( mod 10000)
= (10000 - 143) ( mod 10000)
= 8746
解答・その15
(ペンネ-ム:teki)
答え 8746
問題の5数は、94-1、94-2、94-3、94-4、94-5 です。
下4桁を求める場合、94以上の桁は考える必要がないので、
結局、94-120(10進)の9進法の下4桁を求めればいいわけです。
120=92+4×91+3 なので、10000(9進)-143(9進)=8746
解答・その16
(ペンネ-ム:SOU)
以下、扱う値は全て9進とします。
104 同士の和・差・積は下4桁に依存しませんから、104 の関数Rとしてまとめることにし、
下4桁のみを表す関数をLFD()とすると、
答え = LFD(与式) = LFD( (104 - 1) (104 - 2) (104 - 3) (104 - 4) (104 - 5) ) = LFD(R(104) - 143) = 104 - 143 = 8746 //
解答・その17
(ペンネ-ム:kohji)
以下の式は9進数表記によるものである。
8888*8887*8886*8885*8884=(10000-1) (10000-2) (10000-3) (10000-4) (10000-5)
≡(-1)(-2)(-3)(-4)(-5)
≡-143
≡8746 (mod 10000)
従って与式の下4桁は 8746 である。
解答・その18
(ペンネ-ム:T_Tatekawa)
以下,[ ] で囲まれているのは10進数,そうでないものは
9進数を表す事にします.
9進数で考えると,
8888=10000-1
8887=10000-2
8886=10000-3
8885=10000-4
8884=10000-5
ですので,
8888x8887x8886x8885x8884
=(10000-1)x(10000-2)x(10000-3)x(10000-4)x(10000-5)
です.下4桁だけを考えるので,10000が一つでもかかるかけ算の
結果は影響しないから,
(10000-1)x(10000-2)x(10000-3)x(10000-4)x(10000-5)
= A x 10000 - 1x2x3x4x5
= (A-1) x 10000 + (10000- 1x2x3x4x5)
という形で考えればいいことになります.(Aは定数)
1x2x3x4x5 = [120] = [1x9x9 + 4x9 + 3] = 143
なので,
10000 - 143 = 8746
です.よって下4桁は 8746 です.
解答・その19
(ペンネ-ム:浜田 明巳)
普通に9進法で計算すると,
| 8888(9)×8887(9)×8886(9)×8885(9)×8884(9) | |
| = | (10000(9)-1(9))×(10000(9)-2(9))×(10000(9)-3(9))×(10000(9)-4(9))×(10000(9)-5(9)) |
| ≡ | (-1(9))×(-2(9))×(-3(9))×(-4(9))×(-5(9))(mod 10000) |
| = | -6(9)×22(9) |
| = | -143(9) |
| ≡ | 10000(9)-143(9)(mod 10000) |
| = | 8746(9) |
さらに,UBASIC,十進BASICで検算してみても同じ答が得られる.
(UBASIC) 10 'asave "wm142.ub" 20 dim S(4) 30 A=8+8*9+8*9^2+8*9^3 40 B=7+8*9+8*9^2+8*9^3 50 C=6+8*9+8*9^2+8*9^3 60 D=5+8*9+8*9^2+8*9^3 70 E=4+8*9+8*9^2+8*9^3 80 Seki=A*B*C*D*E 90 for J=1 to 4 100 S(J)=Seki@9 110 Seki=(Seki-S(J))//9 120 next J 130 for J=4 to 1 step -1 140 print right(str(S(J)),1); 150 next J 160 end (十進BASIC) !wm142.bas OPTION ARITHMETIC DECIMAL_HIGH DIM s(4) LET a=8+8*9+8*9^2+8*9^3 LET b=7+8*9+8*9^2+8*9^3 LET c=6+8*9+8*9^2+8*9^3 LET d=5+8*9+8*9^2+8*9^3 LET e=4+8*9+8*9^2+8*9^3 LET seki=a*b*c*d*e FOR j=1 TO 4 LET s(j)=MOD(seki,9) LET seki=(seki-s(j))/9 NEXT j FOR j=4 TO 1 STEP -1 PRINT RIGHT$(STR$(s(j)),1); NEXT j PRINT END
解答・その20
(ペンネ-ム:夜ふかしのつらいおじさん)
8888×8887×8886×8885×8884
=(10000-1)(10000-2)(10000-3)(10000-4)(10000-5)
=100005
-(1+2+3+4+5)×100004
+(1・2+1・3+1・4+1・5+2・3+2・4+2・5+3・4+3・5+4・5)×100003
-(1・2・3+1・2・4+1・2・5+1・3・4+1・3・5+1・4・5+2・3・4+2・3・5+2・4・5+3・4・5)×100002
+(1・2・3・4+1・2・3・5+1・2・4・5+1・3・4・5+2・3・4・5)×10000
-1・2・3・4・5
下4桁の数を知りたいので、次の計算をすれば十分です。
10000-1・2・3・4・5 ・・・(1)
=10000-143
=8746
 ここまでは、九進法の計算です。
ここまでは、九進法の計算です。
(1)の計算は、十進法では、
1×94-5!
=6561-120
=6441
この値は、九進法では、右の計算より、8746となります。
なお、120は九進法では、右の計算より、143です。
正解者
| オヤジ | 夜ふかしのつらいおじさん | teki |
| のっこん | 迷子の雄猫 | T_Tatekawa |
| 転位反応 | スモークマン | 巷の夢 |
| 浜田 明巳 | 杖のおじさん | 赤影 |
| SOU | ミイ | kohji |
| 長崎島原 かがみ | バルタン星人 | ぐりま |
| 三角定規 | こまったコ |
コメント
9進法では、1,2,3,4,5,6,7,8ときて、その次は繰り上がって「10」となります。
この問題にでてくる「8888」という数の次は、繰り上がって「10000」となります。
つまり、「8888=10000-1」です。
同じように、「8887=10000-2」・・ですから、これをうまく利用すると、
複雑な計算を回避することができますね。
 top
top