１４１．単位分数の和
次の□にあてはまる正の整数の組をすべて求めてください。
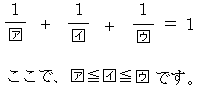
* 「正の」という条件を追加しました。(9/2)
問題の出典
大人のための算数連絡帳 中学入試編
佐藤恒雄
講談社ブルーバックス
慶應義塾普通部
答えと解説
解答・その1
（ペンネ−ム：テレスとアリス）
ア、イ、ウすべて正の数なので、ア＝１は成立しません。
（ア、イ、ウ）＝（２、３、６）
（ア、イ、ウ）＝（２、４、４）
（ア、イ、ウ）＝（３、３、３）
解答・その2
（ペンネ−ム：赤影）
(1)１／３＋１／３＋１／３＝１
(2)１／２＋１／４＋１／４＝１
(3)１／２＋１／３＋１／６＝１
どう考えても以下の３パターンしか思いつきません。
本来ならば、網羅性を示すべきなんでしょうね。
解答・その3
（ペンネ−ム：G3）
これはすなわちピザ好き三人の分配方法の問題であると言っても過言ではないでしょう！
ジャンケンで順番がきまったＡ、Ｂ、Ｃ三人は他の人より先にとる以上、後から取る奴より少ないのは許せない。
(取り分がないのもケンカ。あまらせるわけはない。）
そんなイメージでアは２と３しかありえず、
そのときのイは？ウは？と数字をいれて解きました。（一応暗算でできる程度の式は使いましたが）
自分としては論理的な力技と思っています。
アからオまでとか増えた場合もこのイメージが通用するのか分かりません。
もっと数式で解けたらと思うのですが文系には無理です。
私が出した答えは
ア、イ、ウの順に（３，３，３）（２、３、６）（２、４、４）
どうでしょうか。。。なんかすっきりしないんだよな
解答・その4
（ペンネ−ム：杖のおじさん）
その１ ア→２ イ→４ ウ→４
その２ ア→２ イ→３ ウ→６
その３ ア→３ イ→３ ウ→３
以上３組です。
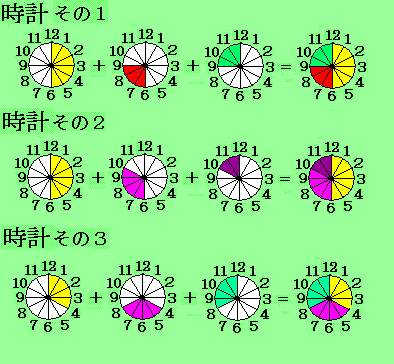
時計をイメージして考えました。
下図の通りです。
解答・その5
（ペンネ−ム：mariki）
答え
（ア・イ・ウ）＝（２・３・６）
＝（２・４・４）
＝（３・３・３）
アは、２か３、しかないと思ったので、ひとつづづ考えました。
解答・その6
（ペンネ−ム：こまったコ）
(ア、イ、ウ)
(2,3,6)
(3,3,3)
(2,4,4)の3組。
なぜかというところはわからないのですが、これ以上分母の数が大きくなると
分子が1の分数3つの和では1を作れないんじゃないかと思います。
解答・その7
（ペンネ−ム：迷子の雄猫）
1/2+1/3+1/6
1/2+1/4+1/4
1/3+1/3+1/3
3つの分数の和が１だから、３つの中で最大の分数は1/3以上。
最初が1/2なら、２つ目が1/5だと合計が１にならない。
よって上記の３通り。
解答・その8
（ペンネ−ム：teki）
答え
（２，４，４） （２，３，６） （３，３，３）
ア＝１は、イ、ウに該当する数がありません。
また、ア＞３だと、３つで１になる数はありません。
で、アは２か３しかありません。
ア＝２ のとき、イ＝３，４しかありませんが、ア＝２、イ＝３のとき、ウ＝６。
ア＝２、イ＝４ のとき、ウ＝４。
ア＝３ のとき、イ＝ウ＝３。
これ以外、条件を満たす数はありません。
なお、（２，３，６）は割と有名ですが、残り２つはひょっとしたらうっかりする
かも知れませんね。
解答・その9
（ペンネ−ム：Ukiki_masamasa）
1. ア=1の場合、
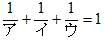を満たす為には イ=ウ=0 となる必要があるので、 ア≦イ≦ウ を満たせない。
2. ア=2の場合、
2-1. イ=2 の場合、ウ=0となり、ア≦イ≦ウを満たさない。
2-2. イ=3 の場合、ウ=6 (ア≦イ≦ウを満たす)
2-3. イ=4 の場合、ウ=4 (ア≦イ≦ウを満たす)
2-4. イ=5 の場合、ウ=3.3333となり、ア≦イ≦ウを満たさない。
よって、イは4以上を取れない。
3. ア=3の場合、
3-1. イ=3 の場合、ウ=3 (ア≦イ≦ウを満たす)
3-2. イ=4 の場合、ウ=2.4となり、ア≦イ≦ウを満たさない。
よって、イは4以上を取れない。
4. ア=4の場合、
ア≦イ≦ウであるから、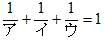の最大値は、
イ=ウ=4の場合で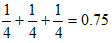 
であり、1に満たない。
よって、アは4以上を取れない。
答え (ア、イ、ウ) = (2、3、6)、(2、4、4)、(3、3、3)
解答・その10
（ペンネ−ム：バルタン星人）
答え
（ア、イ、ウ）＝（２，３，６），（２，４，４），（３，３，３）
プロセス
全て３の時、成立。アは１になれないので２または３
アが２の時、イ＝ウ＝４で成立。イは３または４
イが３の時ウは６
故に答えは上記の３通り。
解答・その11
（ペンネ−ム：転位反応）
与式＝１／ア＋１／イ ＋１／ウ とする
但し、０≦ア≦イ≦ウ
１．整数アの絞込み
ア＝１の場合：任意の整数イ、ウに対して与式＞１
ア＝４の場合：任意の整数イ、ウに対して与式＜１
ア≧５の場合：任意の整数イ、ウに対して与式＜１
２．整数イの絞込み
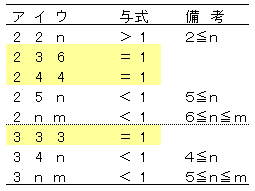
ア＝２、３の場合について調べると以下の通り。
求めるア、イ、ウの組合せは３通り。
解答・その12
（ペンネ−ム：のっこん）
（１/ア）≧１/３ だから １＜ア≦３ よってア＝２、３
(i)ア＝２の時
（１/イ）＋（１/ウ）＝１/２
（１/イ）≧１/４ だから ２＜イ≦４ よってイ＝３、４
１）イ＝３の時 ウ＝６
２）イ＝４の時 ウ＝４
(ii)ア＝３の時
（１/イ）＋（１/ウ）＝２/３
（１/イ）≧１/３ だから イ＝３ この時 ウ＝３
（ア、イ、ウ）＝（２、３、６）、（２、４、４）、（３、３、３）
解答・その13
（ペンネ−ム：オヤジ）
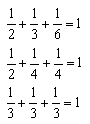
以上の他に、単位分数の和が１となることは無い。
従って ア≦イ≦ウ となる 自然数は、
∴ （ア，イ，ウ）＝（２，３，６），（２，４，４），（３，３，３）の３通り。
解答・その14
（ペンネ−ム：三角定規）
1/x＋1/y＋1/z＝1，x≦y≦z と書くことにします。
x≧2 は明らかだから
1°x＝2 のとき，1/y＋1/z＝(y＋z)/yz＝1/2 ∴ yz＝2(y＋z) ∴ (y−2)(z−2）＝4
y≦z より y−2＝1，z−2＝4 ，または y−2＝2，z−2＝2
∴ y＝3，z＝6，または y＝z＝4
2°x＝3 のとき，1/y＋1/z＝(y＋z)/yz＝2/3 ∴ yz＝(3/2)(y＋z) ∴ (y−3/2)(z−3/2）＝9/4
y≧3 で y，z が整数になるのは，ｙ−3/2＝z−3/2＝3/2 のときだけで，このとき y＝z＝3
3°x≧4 のとき 1/z≦1/y≦1/x≦1/4 で，1/x＋1/y＋1/z≦3/4 となり，題意を満たさない。
以上より，求める x，y，z は，(x，y，z)＝(2，3，6)，(2，4，4)，(3，3，3)
解答・その15
（ペンネ−ム：巷の夢）
問題を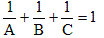 
と
書き換え、条件をＡ≦Ｂ≦Ｃとする。
すると、上記式を満たすＡ、Ｂ、Ｃは以下の場合に限定される。
(1) Ａ＝Ｂ＝Ｃ
(2) Ａ＜Ｂ＝Ｃ
(3) Ａ＝Ｂ＜Ｃ
(4) Ａ＜Ｂ＜Ｃ
(1)の場合は、3/Ａ＝1よりＡ＝Ｂ＝Ｃ＝3
(2)の場合は、Ａ＝Ｎとすると 2/Ｂ＝（Ｎ-1）/ＮよりＢ＝Ｃ＝2Ｎ/（Ｎ-1）＝2+2/（Ｎ-1）となる。
これよりＮ-1は2の倍数であるから1か2しかとれない。そこでこの関係を使い、
Ｎ＝Ａ＝2とすると Ｂ＝Ｃ＝4
Ｎ＝Ａ＝3とすると Ｂ＝Ｃ＝3 即ち(1)の場合となる。
(3)の場合も(2)と同じ式となるが、Ｃと同じ、ないしＣより小さなＡ、Ｂの整数は存在しない。
(4)の場合は、
まずＡの値をＮとしてみると、1/Ｂ+1/Ｃ＝（Ｎ-1）/Ｎとなる。即ちＡ＝Ｎ＝2の時、
1/Ｂ+1/Ｃ＝1/2 そこでＢ＝3とするとＣ＝6となる。
この調子で続けると、1/Ｂ+1/Ｃの右辺は2/3,3/4,4/5、5/6・・・・・・とどんどん1/2よりおおきくなり、1に近づく。
ところが、ＢとＣは異なる数であるため必ず1/2より小さい値にしかならない。因って、これ以上の解は存在しない。
これらをまとめると、
Ａ Ｂ Ｃ
2 3 6
2 4 4
3 3 3となる。
以 上．
解答・その16
（ペンネ−ム：T_Tatekawa）
まず，ア≦イ≦ウなので，ア＝イ＝ウの場合を考えると、
ア＝イ＝ウ＝３で成り立ちます．
アは３以下です．４以上だとどうやっても左辺が１より
小さくなります．
アを１にすると成り立たないので，アを２にします．
残りは １／イ＋１／ウ＝１／２ です．
イに３を入れると，ウが６になります．
イに４を入れると，ウも４です．
イが５以上だとウはイより大きくなるのでだめです．
以上から
ア＝イ＝ウ＝３
ア＝２，イ＝３，ウ＝６
ア＝２，イ＝ウ＝４
の３通りです．
解答・その17
（ペンネ−ム：浜田 明巳）
エクセルのマクロで解きました．
常識的にア，イ，ウに正の整数が入るとすると，
(ア,イ,ウ)=(2,3,6),(2,4,4),(3,3,3)
Option Explicit
Const max As Integer = 1000
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Dim a As Integer
Dim b As Integer
Dim c As Integer
For a = 2 To max
For b = a To max
If 1 / a + 1 / b < 1 Then
c = Int(1 / (1 - 1 / a - 1 / b))
If 1 / a + 1 / b + 1 / c = 1 And b <= c Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = a
Cells(Cells(1, 1).Value, 3).Value = b
Cells(Cells(1, 1).Value, 4).Value = c
End If
End If
Next b
Next a
End Sub
ア，イ，ウに単なる整数が入るとすると，上記の解の他に
(ア,イ,ウ)=(-n,1,n) (nは正の整数)が解となる．
Option Explicit
Const max As Integer = 1000
Sub Macro2()
Sheets("Sheet2").Select
Cells(1, 1).Value = 0
Dim a As Integer
Dim b As Integer
Dim c As Integer
For a = -max To max
If a <> 0 Then
For b = a To max
If b <> 0 Then
If 1 / a + 1 / b <> 1 Then
c = Int(1 / (1 - 1 / a - 1 / b))
If c <> 0 Then
If 1 / a + 1 / b + 1 / c = 1 And b <= c Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = a
Cells(Cells(1, 1).Value, 3).Value = b
Cells(Cells(1, 1).Value, 4).Value = c
End If
End If
End If
End If
Next b
End If
Next a
End Sub
数学的に解くと，次のようになります．
負の数が出て来る解は明らかなので，
１／ａ＋１／ｂ＋１／ｃ＝１，２≦ａ≦ｂ≦ｃ，ａ，ｂ，ｃは自然数とする．
０＜ａ≦ｂ≦ｃから，１／ｃ≦１／ｂ≦１／ａ
∴１／ａ＋１／ｂ＋１／ｃ≦１／ａ＋１／ａ＋１／ａ
∴１≦３／ａ
ａ＞０なので，ａ≦３
ａ≧２から，２≦ａ≦３
ａは自然数なので，ａ＝２，３
i). ａ＝２のとき，１／２＋１／ｂ＋１／ｃ＝１，２≦ｂ≦ｃ
∴１／ｂ＋１／ｃ＝１／２
０＜ｂ≦ｃから，１／ｃ≦１／ｂ
∴１／ｂ＋１／ｃ≦１／ｂ＋１／ｂ
∴１／２≦２／ｂ
ｂ＞０なので，ｂ≦４
ｂ≧２から，２≦ｂ≦４
ｂは自然数なので，ｂ＝２，３，４
ｂ＝２のとき，１／２＋１／ｃ＝１／２，すなわち１／ｃ＝０となり，矛盾する．
ｂ＝３のとき，１／３＋１／ｃ＝１／２
∴ｃ＝６
これはｂ≦ｃ，ｃは自然数であることに適する．
ｂ＝４のとき，１／４＋１／ｃ＝１／４
∴ｃ＝４
これはｂ≦ｃ，ｃは自然数であることに適する．
ii). ａ＝３のとき，１／３＋１／ｂ＋１／ｃ＝１，３≦ｂ≦ｃ
∴１／ｂ＋１／ｃ＝２／３
前と同様に，
∴１／ｂ＋１／ｃ≦１／ｂ＋１／ｂ
∴２／３≦２／ｂ
ｂ＞０なので，ｂ≦３
ｂ≧３から，ｂ＝３
∴１／３＋１／ｃ＝２／３
∴ｃ＝３
これはｂ≦ｃ，ｃは自然数であることに適する．
まとめると，・・・
解答・その18
（ペンネ−ム：夜ふかしのつらいおじさん）
●まず、腕力で解いてみます。
整数ａ，ｂ，ｃの大小はあとで考えます。
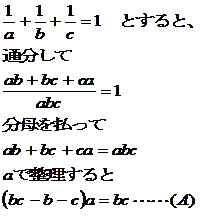
(i)ａ＝１ のとき、（A)を整理すると、ｂ＝−ｃ なので
ｋを自然数として
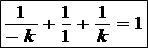
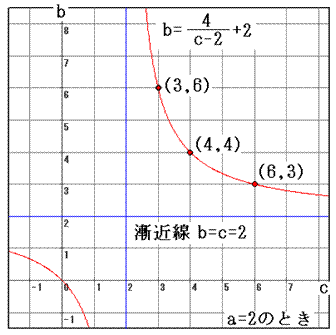
(ii)ａ＝２ のとき、（A)を整理すると、
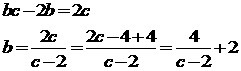
グラフの格子点の座標を読んで、
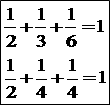
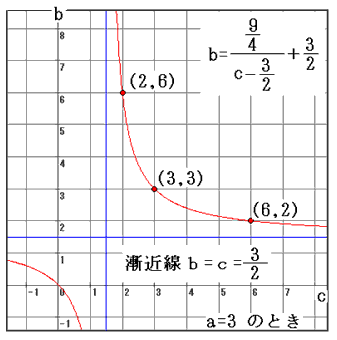
(iii)ａ＝３ のとき、（A)を整理すると
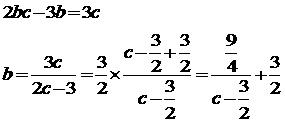
グラフの格子点の座標を読んで、
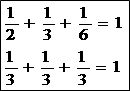
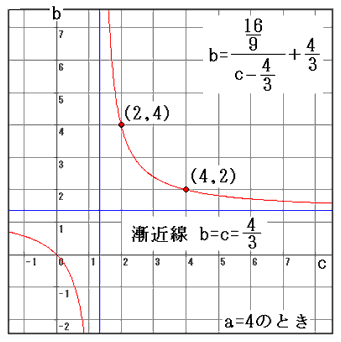
(iv)ａ＝４ のとき、（A)を整理すると
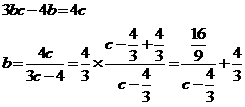
グラフの格子点の座標を読んで、
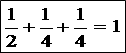
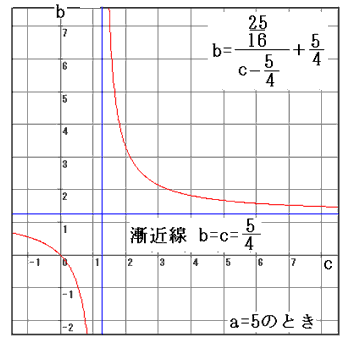
(v)ａ＝５のとき、（A)を整理すると
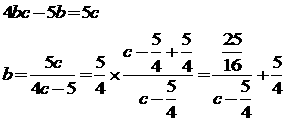
グラフをみると格子点がありません。
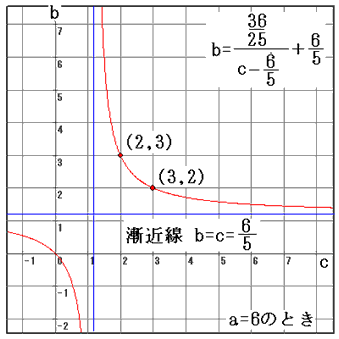
(vi)ａ＝６のとき、（A)を整理すると
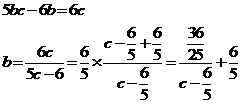
グラフの格子点の座標を読んで、
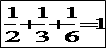
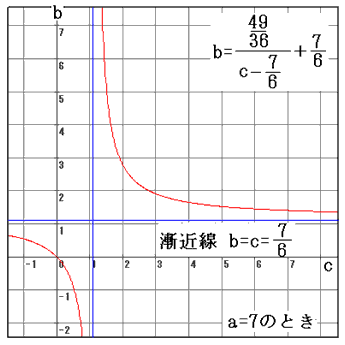
(vii)ａ＝７のとき、（A)を整理すると
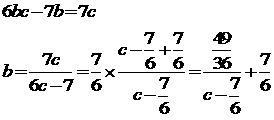
グラフをみると格子点がありません。
このあと、ａ＞７で格子点はありません。
漸近線が＋１に近づき、グラフが漸近線に近づくからです。
ａ，ｂ，ｃを正の整数とすると解答は
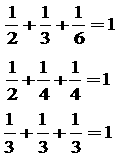
の３つです。
●別解
単位分数には、次の大小関係があります。
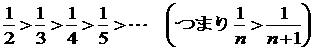
すると、
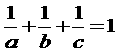
を満たす自然数a,b,cは｛2,3,4,5,6｝のどれかになり、7以上の自然数はありません。
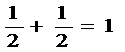
なので、三つの数の一番小さいものは、
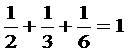
から6と分かります。
｛2,3,4,5,6｝の五つの中から重複を許して三つ取る組み合わせを調べればもれがありません。
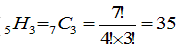
なのでしらみつぶしに35通りを調べます。
(i)3数が同じ場合。
| 2だけ使うとき | × | |
| 3だけ使うとき | → |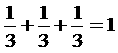 
|
| 4だけ使うとき | × | |
| 5だけ使うとき | × | |
| 6だけ使うとき | × |
(ii)2数が同じ場合（どちらかを２回使う）
| 2,3を使うとき | × | |
| 2,4を使うとき | → |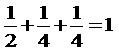 
|
| 2,5を使うとき | × | |
| 2,6を使うとき | × | |
| 3,4を使うとき | × | |
| 3,5を使うとき | × | |
| 3,6を使うとき | × | |
| 4,5を使うとき | × | |
| 4,6を使うとき | × | |
| 5,6を使うとき | × |
(iii)3数が異なるとき
| 2,3,4を使うとき | × | |
| 2,3,5を使うとき | × | |
| 2,3,6を使うとき | → |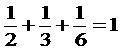 
|
| 2,4,5を使うとき | × | |
| 2,4,6を使うとき | × | |
| 2,5,6を使うとき | × | |
| 3,4,5を使うとき | × | |
| 3,4,6を使うとき | × | |
| 3,5,6を使うとき | × | |
| 4,5,6を使うとき | × |
以上のように三通りあります。
解答・その19
（ペンネ−ム：ＳＯＵ）
1/2,1/3,1/4,1/5,1/6,・・・
のような形の3つの数を足して1になるようにするという行為は、
180°,120°,90°,72°,60°,・・・
の扇形を重ならないように組み合わせて円にする事と同じです。
この考え方だと分数の計算がなくなります。
後者で考えると、例えば
1/2 + 1/4 + 1/4 = 1
の場合は、
のようになります。
以下、この考え方で。
i)最大の角が180°の時
二番目の角は・・・
イ)180°を取ると3つ目が取れないのでだめ。
ロ)120°を取ると残りは60°が取れるのでok
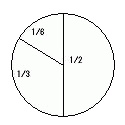
ハ) 90°を取ると残りは90°が取れるのでok
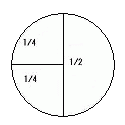
ニ)これ以上小さい角は、もう一つの角と大小関係が逆転するので無意味。
ii)最大の角が120°の時
二番目の角は・・・
ホ)120°を取ると残りは120°が取れるのでok
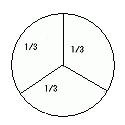
ヘ)これ以上小さい角は、もう１つの角と大小関係が逆転するので無意味。
iii)最大の角が120°より小さい時
残り二つの角のうち、少なくとも一方は120°よりも大きくなってしまうので、
考察は無意味。
以上から、この三つは答えとなる組み合わせであり、かつ、これ以外には存在しない。
正解者
| teki | 杖のおじさん | T_Tatekawa |
| 迷子の雄猫 | 巷の夢 | オヤジ |
| 浜田 明巳 | こまったコ | G3 |
| 転位反応 | 夜ふかしのつらいおじさん | ＳＯＵ |
| のっこん | mariki | テレスとアリス |
| 赤影 | Ukiki_masamasa | 三角定規 |
| バルタン星人 |
コメント
問題の条件を満たす正の整数の組を求めると、３組になります。すべて求める、ということは、
これ以外にはないということも示す必要があります。
問題を視覚化するというのは、その問題の理解に大変役だつことだと思いますが、
夜ふかしのつらいおじさんが双曲線上の格子点を
探すという解法、杖のおじさんやＳＯＵさん
が円を扇型で分割していくという解法は寄せてくださいましたが、
とてもユニークで素晴らしいと思います。
top