Challenge!

問題140　各位の積
Weekend Mathematics／問題／問題140　各位の積

１４０．各位の積

０以上の整数nに対して、f(n)=（10進法でnを表したときの各位の積）と約束する。 ただし、n=0の場合は特別に、f(0)=0と約束する。
例えば
f(2223)=2×2×2×3=24、f(f(2223))=2×4=8　である。

(1) ３桁の正の整数nで、f(n)=105　を満たす最小の数を求めよ。
(2) ４桁の正の整数nで、f(n)=210　を満たす最大の数を求めよ。
(3) ５桁の正の整数nで、f(n)=1024　を満たすものはいくつあるか。
(4) 正の整数nで、f(f(2005n))≠0　を満たす最小のものを求めよ。

問題の出典

広中杯ハイレベル中学数学に挑戦
算数オリンピック委員会監修
講談社ブルーバックス
2005年ファイナル問題

答えと解説

解答・その1

（ペンネ－ム：長崎島原　かがみ）

(1)　１０５＝３×５×７　だから　最小の数は　３５７


解答・その2

（ペンネ－ム：三角定規）

(1) f(n)＝105＝3・5・7 及び n は 3 桁だから，n の各位の数は 3，5，7。
よって，そのような n の最小数は，３５７　…[答]

(2) f(n)＝210＝2・3・5・7＝1・5・6・7 及び n は 4 桁だから，
そのような n の最大数は，７６５１　…[答]



解答・その3

（ペンネ－ム：テレスとアリス）

(1) 3数の積が105になるのは1通りです
　　　105＝3×5×7
最小の数は 357 です。

(2) 4数の積が210になるのは2通りです
　　　210＝2×3×5×7
　　　210＝1×5×6×7
最大の数は 7651 です。

(3) 1024＝210 となります
5数の積が1024になるのは、
　　　20、 21、 22、 23
から5数を組み合わせ、その指数の合計が10となるときです

グループ１＝（20、21、23 、23 、23）
　　　12888、18288、18828、18882、
　　　21888、28188、28818、28881、
　　　81288、81828、81882、82188、
　　　82818、82881、88128、88182、
　　　88218、88281、88812、88821
グループ２＝（20、22、22 、23 、23）
　　　14488、14848、14884、18448、
　　　18484、18844、41488、41848、
　　　41884、44188、44818、44881、
　　　48148、48184、48418、48481、
　　　48814、48841、81448、81484、
　　　81844、84148、84184、84418、
　　　84481、84814、84841、88144、
　　　88414、88441
グループ３＝（21、21、22 、23 、23）
　　　22488、22848、22884、24288、
　　　24828、24882、28248、28284、
　　　28428、28482、28824、28842、
　　　42288、42828、42882、48228、
　　　48282、48822、82248、82284、
　　　82428、82482、82824、82842、
　　　84228、84282、84822、88224、
　　　88242、88422
グループ４＝（21、22、22 、22 、23）
　　　24448、24484、24844、28444、
　　　42448、42484、42844、44248、
　　　44284、44428、44482、44824、
　　　44842、48244、48424、48442、
　　　82444、84244、84424、84442
グループ５＝（22、22、22 、22 、22）
　　　44444

答えは、101個です。

解答・その4

（ペンネ－ム：赤影）

(1)105を素因数分解すると105=3*5*7　よって、求める数は357。

(2)210=2*3*5*7、求める数は7651

(3)1024＝210である。
よって求める数をＡＢＣＤＥとすると、Ａ，Ｂ，Ｃ，Ｄ，Ｅはいずれも2のべき乗で あり、それぞれ1以上9以下であるから、1,2,4,8のいずれかとなる。
ここで、ABCDEの積が1024になるパターンとしては
1024=8*8*8*2*1 -->ア（8が3個、2が1個、1が1個）
　　=8*8*4*4*1　-->イ（8が2個、4が2個、1が1個）
　　=8*8*4*2*2　-->ウ（8が2個、4が1個、2が2個）
　　=8*4*4*4*2　-->エ（8が1個、4が3個、2が1個）
　　=4*4*4*4*4　-->オ（4が4個）
の５パターンであり、
アと同じ系列（並びが別のもの）は=20通り(※1参照）
イと同じ系列は30通り（※２参照）
ウと同じ系列は30通り（※３参照）
エと同じ系列は20通り（※４参照）
オと同じ系列は1通り（これは明らか）
よって、求める値は上記全ての場合の数を足して、20+30+30+20+1＝101個・・・答え

※１　8*8*8*2*1の系列の場合の数
これは箱が5つあり、その中の２つに１と２を順序を区別して並べたときの場合の数 に等しい。よって、求める場合の数は5P2＝5*4=20通り
※２　8*8*4*4*1の系列の場合の数
まず、最上位を1のときの場合の数を考え。次の桁は4か8である。 4にすると、残りは4,8,8である。4の位置を考えると3通り。 8にすると、残りは8,4,4である。8の位置を考えると同様に3通り。
次に、最上位が4であるとする。 残るは1,4,4,8となる。 2桁目が1ならばのこりは4,4,8⇒8の位置を考えると3通り。 2桁目が4ならばのこりは1,4,8⇒3P2=6通り 2桁目が8ならばのこりは1,4,4⇒1の位置を考えると3通り
最後に最上位が8であるとする。 これは１つ上の場合において、4と8が入れ替わっただけであるので この場合の数は3+6+3=12通り
これで全部であるので、※２の場合の数は3+3+12+12＝30通り
※３　8*8*4*2*2の系列の場合の数
　 これは、※２における2を4、1を2に書き替えたものであるので、場合の数としては ※２と同じ30通りとなる。
※４　8*4*4*4*2の系列の場合の数
これは、※１における8を4、1を8に書き替えたものであるので、場合の数としては ※１と同じ20通りとなる。


解答・その5

（ペンネ－ム：スモークマン）

(1)105=3*5*7だから、357
(2)210=2*3*5*7だから、7651
(3)1024=210だから、23=8 以上は1桁でないので、
10=3+3+3+1・・・5C3*2C1=20
　=3+3+2+2・・・5C2*3C2=10*3=30
　=3+3+2+1+1・・・5C2*3C1=10*3=30
　=(3+3+1+1+1+1)
　=3+2+2+2+1・・・5C1*4C3=20
　=(3+2+2+1+1+1)
　=(3+2+1+1+1+1+1)
　=(3+1+1+1+1+1+1+1)
　=2+2+2+2+2・・・5C5=1
　=(2+2+2+2+1+1)
　=(2+2+2+1+1+1+1)
　=(2+2+1+1+1+1+1+1)
　=(2+1+1+1+1+1+1+1+1)
　=(1+1+1+1+1+1+1+1+1+1)

合計＝20*2+30*2+1=101


解答・その6

（ペンネ－ム：Ukiki_masamasa）

(1)
f(n) = 105
= 3*5*7 最小だから　Ans. 357

(2)
f(n) = 210
= 2*3*5*7 最大だから Ans. 7651

(3)
f(n) = 1024= 210
　5桁だから次の4つの数字の組合せが考えられる
= 4*4*4*4*4　→　44444　の1通り
= 8*4*4*4*2　→　24448～84442　の20通り
= 8*8*4*2*2　→　22488～88422　の30通り
= 8*8*4*4*1 →　14488～88441　の30通り
= 8*8*8*2*1　→　12888～88821　の20通り
　　よって合計101通り　　　　　Ans. 101通り

(4)
命題成立の為には「2005×n」がゼロを含まなくなる様にｎを決めればよい。
ゼロを含まないためには、末尾が5であるのでｎは奇数でなくてはいけない。
また、「2005×n」（ｎは奇数）の場合、末尾が常に5になるので、「2005×n」の桁のどこかに偶数があるとf(2005*n)にゼロが含まれてしまい、命題が成り立たなくなる。つまり、「2005×n」は全ての桁が奇数でなくてはいけない。
エクセルでn=3から順に計算させると n=267 の時に
f(f(2005*267)) = f(535335) = 3375 となり、命題が初めて成立する。
　　よって、　　Ans. n=267

解答・その7

（ペンネ－ム：teki）

１　３５７
２　７６５１
３　１０１通り
４　２６７

１は、１０５＝３×５×７なので、最小は３５７、最大は７５３です。
　（３×５、５×７、３×７はいずれも２桁）
２も、２１０＝２×３×５×７なので、４桁の最小は１５６７、
　最大は７６５１（これは、２×３＝６が１桁なので要注意。つい７５３２とやってしまいそうですね。）
３は、１０２４＝２１０>/sup>なので、１０を３以下の自然 数の和に分解する方法に帰着します。
　並べ方を考慮すると、
（０，１，３，３，３）が２０通り、
（１，１，２，３，３）が３０通り、
（１，２，２，２，３）が２０通り、
（０，２，２、３，３）が３０通り、
（２，２，２，２，２）が１通りの計１０１通りとなります。
４は、ｎ＝２６７でようやくｆ（ｆ（２００５ｎ））＝ｆ（３３７５）＝３１５
で条件を満たすようです。 一応、エクセルで２１以上の奇数に２００５をかけて確かめましたが、 これって、何かうまい解法があるんでしょうか？

解答・その8

（ペンネ－ム：迷子の雄猫）

（１）357

（２）7651
素因数分解して、考えました。

（３）101通り
正の１桁の整数を、５つ掛け合わせて1024になる組み合わせは以下の通り。
(8,8,8,2,1)...20通り：p(5,5) / p(3,3) = 5*4*3*2*1 / (3*2*1)=20
(8,8,4,4,1)...30通り：p(5,5) / p(2,2) / p(2,2) = 5*4*3*2*1 / (2*1) /(2*1)=30
(8,8,4,2,2)...30通り：p(5,5) / p(2,2) / p(2,2) = 5*4*3*2*1 / (2*1) /(2*1)=30
(8,4,4,4,2)...20通り：p(5,5) / p(3,3) = 5*4*3*2*1 / (3*2*1)=20
(4,4,4,4,4)...1通り：

（４）267
2005に偶数をかけると10で割り切れるからf(f(2005n))=0
2005に奇数をかけると末尾が５だから、2005ｎの結果に偶数が含まれるとf(f(2005n))=0
あとは力技です。

解答・その9

（ペンネ－ム：オヤジ）

（１）素因数分解すると　１０５＝３×５×７
　∴　３５７
（２）素因数分解すると　２１０＝２×３×５×７
また、２×３＝６：１桁の自然数　，
　∴　７６５１
（３）５桁の自然数　ｆ（ｎ）＝１０２４＝２１０
　 ２０＝１，２１＝２，２２＝４，２３＝８　：１桁の自然数
　（Ⅰ）　（８，８，８，２，１）を用いる自然数：　２０通り
　（Ⅱ）　（８，８，４，４，１）を用いる自然数：　３０通り
　（Ⅲ）　（８，８，４，２，２）を用いる自然数：　３０通り
　（Ⅳ）　（８，４，４，４，２）を用いる自然数：　２０通り
　（Ⅴ）　（４，４，４，４，４）を用いる自然数：　１通り
（Ⅰ）～（Ⅴ）より
２０＋３０＋３０＋２０＋１＝１０１
　∴　１０１　通り
（３） ２００５×ｎ　は、５の倍数なので、各桁が全て奇数となる事が必要、
∴　ｎ＝２６７

解答・その10

（ペンネ－ム：こまったコ）

(1) 105を因数分解すると　105 = 3 x 5 x 7 なので　n =357
(2) 210を因数分解すると　210 = 2 x 3 x 5 x 7
この因数のうち、2と3をかけると6。1桁分足りないので1を追加して　n = 7651
(3) 1024を因数分解すると　1024 = 210
桁の数として使えるのは 21=2, 22=4, 23=8 の3つのみ。
必要に応じて1も使える。

<1> 5桁のうちどこかに8が1つ入る場合。
8を作るのに2を3つ使うので残りは7個。22 を3つ、21を1つ作ればよい。
よって5桁に使うのは　2, 4, 4, 4, 8。
2が万の位の時は8がどの位に入るかで4通り。
8が万の位の時は2がどの位に入るかで4通り。
4が万の位の時は残りの2つの4がどこに入るかで6通りx それぞれの場合で残りの桁に2と8のどちらが入るかで2通りで12通り。
よって<1>の条件でできる5桁の数は計20個。

<2> 5桁のうちどこかに8が2つ入る場合。
8を2つ作るのに2を6つ使うので残りは4個。
その1：22=4を2個、1を1個使う場合、5桁に使うのは　1, 4, 4, 8, 8。
1が万の位の時は千くらいが4の時で3通り、8の時で3通りの計6通り。
4が万の位の時は千くらいが1の時で3通り、4の時で3通り、8の時で6通りの計12通り。
8が万の位の時も12通り。
よって合計30通り。
その2：22=4を1個、2を2個使う場合、5桁に使うのは　2, 2, 4, 8, 8。
使う数の組み合わせは違うが、「その1」の時と同じ考え方ができるので
「その2」の条件でできる5桁の数は合計30個。
よって<2>の条件でできる5桁の数は計60個。

<3> 5桁のうちどこかに8が3つ入る場合。
8を3つ作るのに2を9つ使うので残りは1個。よって5桁に使うのは　1, 2, 8, 8, 8。
これは<1>の条件と同じ考え方ができるので
<3>の条件でできる5桁の数字は計20個。

<4> 5桁のうちどこにも8が入らない場合は　44444の1つ。

<1>+<2>+<3>+<4>=20+60+20+1=101

よって5桁の正の整数nで、f(n)=1024　を満たすものは全部で101個。

(4) どの整数も0を掛けたら0になるので2005 x n　の答えの各桁に0がないようにする必要がある。
自力で計算するのが面倒なのでエクセルを使い、2005 x 1, 2005 x 2...を計算したところ、
積のどの桁にも0が含まれない最小の積は n=23の時の　2005 x 23 = 46115
f(f(46115))を計算すると　4 x 6 x 1 x 1 x 5 = 120
120にゼロが含まれるので　f(f(2005n))≠0を満たさない。
f(2005n)の答えの1の位は0か5で、0になるのは n が偶数の時。
よって条件をnは奇数でなければならず、1の位は5である。
また、f(2005n)の各桁に使われる数に偶数が含まれていると
1の位の5と掛けた時一の位が0になる数ができてしまうので
f(2005n)の各桁に使われる数はすべて奇数でなければならない。

以上のすべての条件を満たす最初の n は 267。
(これはエクセルの計算式から探しました。)
f(2005x267)=f(535335)=5 x 3 x 5 x 3 x 3 x 5 = 3375
f(3375) = 3 x 3 x 7 x 5 = 315 ≠0　である。
よって n = 267

解答・その11

（ペンネ－ム：G3）

（１）3×5×7=105（素因数分解って言うんでしたっけ）
だから小さいほうから並べて『357』
答え　n=357（だ！）

（２）2×3×5×7=210
大きいほうから並べて『7532』と言いたいが、2×3=6だから 1×5×6×7=210。それで『7651』
単純に素因数分解してはいけないのか？
一桁のなるべく大きい因数に分解すればいいのか？
とにかく
答え　n=7651（だといいが・・）

（３）1024=2の10乗だからこんな風に考えました。かなり細かく状況設定していますが・・（ボクはイメージ派）
『ピンポン玉が3個まで入るメスシリンダーが5本あって 区別のつかない１０個のピンポン玉を入れる場合何通りあるのか？ 玉が入っていないメスシリンダーがあってもいい。
玉の分け方をまず考え、後で並び替える場合の数を考えました。
　(i)玉の入り方が３３３１０のとき器の並び方は、5!/3!=20
　(ii)３３２２０のときは5!/2!・2!=30
　(iii)３３２１１ときは同様に（この書き方ラク！）30
　(iv)３２２２１のときは20
　(v)２２２２２のときは1は明らか。
それぞれの場合の数を足して101。
答え　101ある！（と思う）

（４）一の位が5であることを考えて 2005nが最小で各位奇数になるようなnを見つけるわけですよね？そこで、
2005n=(2000+5)n
　(i)5n注目。に千の位が偶数（２）だから、この桁以下を奇数にするためにはnが少なくとも223以上の奇数。
　(ii)2000nに注目してとりあえずn=223を代入してみる。2000×223=446000
これを見ながら考えました。
ココから説明がうまくないのですが（結構省きます） 5nは上二桁には影響を及ぼさないから
上二桁が奇数になるためには2000の倍数で最小のものを見つける必要がある。
そして上二桁が奇数になる条件はnの十位、一位は繰り上がりのある5以上。
すると(i)の条件も考えて255＜=n。
ここもとりあえず一の位だけやってみる。（2005×255=511275でもいいんですが・・）
255×5=1275（だめだ）
これ以上で最小の各位奇数は1375
1375÷5=265
そろそろ元に代入して
(2000+5)×265=53000+1325=531325
十の位が偶数だから次に小さい奇数267で
2005×267=535335（！！）
全部奇数だ。かなり運動部的な解法でした。
答えは　n=267（であることを祈る）

解答・その12

（ペンネ－ム：mariki）

（１）105＝3×5×7　∴答 357

（２）210＝2×3×5×7　または
＝1×5×6×7　
　∴答 7651

（３）　1024＝2×2×2×2×2×2×2×2×2×2
５桁の整数なので
　　４４４４４・・・・・１通り
　　８４４４２・・・・・２０通り　　（5×4×3×2×1）÷（3×2×1）
　　８８８２１・・・・・２０通り　　（上記と同じ）
　　８８４２２・・・・・３０通り　　（5×4×3×2×1）÷（（2×1）×（2×1））
　　８８４４１・・・・・３０通り　　（上記と同じ）
　∴答 １０１個
　　　　　　　　　　　　　

（４）　2005×ｎの結果で各位の数に、０及び偶数が無いものを探しました。
エクセルに式を入れて出して見ました。
結果、ｎ＝２６７で
ｆ（ｆ（2005×267））＝ｆ（ｆ（535335））＝ｆ（3375）＝315
　∴答 ｎ＝267

解答・その13

（ペンネ－ム：バルタン星人）

答え
(1) ３５７
(2) ７６５１
(3) １０１通り
(4) ２６７

プロセス
（１）素因数分解すると３×５×７、１えお含めることは困難なので３５７が最小
（２）２１０を素因数分解すると２×３×５×７、この中で２×３＝６なので １を含めることが可能になる。故に７６５が最大
（３）１０２４は２の１０乗、まず１，２，４，８の組合せが考えられる。 簡単にするためべき乗数０，１，２，３で考え和が１０になる組合せを考える。
　（０１３３３）２０通り
　（０２２３３）３０通り
　（１１２３３）３０通り
　（１２２２３）２０通り
　（２２２２２）１通り　　　計１０１通り
（４）ｆ（ｎ）≠０になるのは、各位に０を持たないとき。 まず２００５ｎが０を持たないのが条件、また末尾は５になるので 各位が奇数になるのが条件
ここからちょっとずるをし、エクセルでｎ×２００５をｎ＝１からシラミつぶし に調べると
最小のｎは２６７でｆ（５３５３３５）＝３３７５となる。

解答・その14

（ペンネ－ム：杖のおじさん）

答え　１→357 2→7651 3→101通り 4→267

問題１
f (n)=105=1×105=1×3×35=1×3×5×7=3×5×7
３桁で最小の数字という条件なので答えは３５７です。

問題２
f (n)=210=1×210=1×2×105=1×2×3×35=1×2×3×5×7=1×6×5×7
４桁で最大の数字という条件なので答えは７６５１です。

問題３
１０２４＝２１０＝２×２×２×２×２×２×２×２×２×２＝f（2222222222）
この１０桁を５桁にします。それには次の５パターンがあります。
　８×８×８×２×１・・・・・１
　８×８×４×４×１・・・・・２
　８×８×４×２×２・・・・・３
　８×４×４×４×２・・・・・４
　４×４×４×４×４・・・・・５
それぞれの組み合わせを考える。
１と４は（５×４×３×２×１）÷（３×２×１）＝２０通り
２と３は（５×４×３×２×１）÷（２×１）÷（２×１）＝３０通り
５は１通り
　合計２０＋３０＋３０＋２０＋１＝１０１通り
　答え１０１通り

問題４
f（f（2005n））‡0を満たすnを見つける。
ｆ（Ｎ）のＮの桁の中に０があるか又は偶数と５が両方ある場合はf(N)=0になります。
従って全桁奇数になるnを見つけます。
２００５×nのnを１，２，３・・・と変えて確認しました。
エクセルを使って確認しました。その結果n=267で５３５３３５となりました。
従って答えは２６７です。

解答・その15

（ペンネ－ム：転位反応）

(1) 3桁の整数を作るために、105を素因数分解して105=3×5×7
これらの素数の組合せから1桁の合成数は生成できないので、求める3桁の整数はn=357

(2)4桁の整数を作るために、 210を素因数分解して210=2×3×5×7
合成数を使用して2×3＝1×6とすると、210=1×5×6×7
よって、求める４桁の整数はｎ=7651

(3) 1024=210なので、以下の５桁の整数に分解できる
　　　1024=4×4×4×4×4
　　　1024=2×8×4×4×4
　　　1024=1×8×8×4×4
　　　1024=1×2×8×8×8
　　　1024=2×8×2×8×4

(i)1024=4×4×4×4×4の場合：１通り
　　　4 4 4 4 4
(ii)1024=2×8×4×4×4の場合：20通り
　　　2 8 4 4 4、2 4 8 4 4、2 4 4 8 4、 2 4 4 4 8、4 2 8 4 4、4 2 4 8 4
　　　4 2 4 4 8、4 4 2 4 8、4 4 2 8 4、 4 4 4 2 8、4 4 4 8 2、4 4 8 2 4
　　　4 4 8 4 2、4 8 2 4 4、4 8 4 2 4、 4 8 4 4 2、8 2 4 4 4、8 4 2 4 4
　　　8 4 4 2 4、8 4 4 4 2
(iii)1024=1×8×8×4×4の場合：30通り
　　　1 8 8 4 4、1 4 4 8 8、1 4 8 4 8、 1 4 8 8 4、1 8 4 4 8、1 8 4 8 4
　　　4 4 1 8 8、4 4 8 1 8、4 4 8 8 1、 4 1 4 8 8、4 1 8 4 8、4 1 8 8 4
　　　4 8 1 4 8、4 8 1 8 4、4 8 4 1 8、 4 8 4 8 1、4 8 8 1 4、4 8 8 4 1
　　　8 1 4 4 8、8 1 4 8 4、8 1 8 4 4、 8 4 1 4 8、8 4 1 8 4、8 4 4 1 8
　　　8 4 4 8 1、8 4 8 1 4、8 4 8 4 1、 8 8 4 4 1、8 8 4 1 4、8 8 1 4 4

(iv)1024=1×2×8×8×8の場合：20通り
　　　(ii)と同じパターンなので

(v)1024=2×8×2×8×4の場合：30通り
　　　(iii)と同じパターンなので

以上より、101通り

(4) f(f(2005n))≠0　を満たすためには、2005nの各位は全て奇数であることが必要
よって、整数ｎは奇数である
(i)nが１桁の奇数aの場合
2000a+5aにおいて、百位は常にゼロなので、f(f(2005n))=0

(ii)nが2桁の奇数ａｂの場合
20000a+2000b+50a+5bにおいて、一位は５、千位は常に偶数となるので、f(f(2005n))=0

(iii)nが３桁の奇数ａｂｃの場合、200000a+20000b+2000c+500a+50b+5cとおく
千位を奇数にするためには、500aからの繰り上がりを必要とするため　ａ≧２
十万位を奇数にするためには、20000bからの繰り上がりを必要とするため　b≧5
一万位を奇数にするためには、2000cからの繰り上がりを必要とするため　c≧5
よって、255以上の奇数、255,257,259,265,267,...について検証するとｎ=267は題意を満たす
f(f(2005n))=f(f(2005×267)=f(535335)=3375


解答・その16

（ペンネ－ム：のっこん）

（１）105＝3・5・7　　最小は357

（２）210＝2・3・5・7＝1・6・5・7　　最大は7651

（３）1024＝210
10を、0以上3以下の5つの整数に分割する方法は
(1) 0,1,3,3,3　(2) 0,2,2,3,3　(3) 1,1,2,3,3　(4) 1,2,2,2,3　(5) 2,2,2,2,2
(1)の並べ替えは5！/3！＝20通り
(2)の　　　〃　　　5！/（2！2！）＝30通り
(3)の　　　〃　　　30通り
(4)の　　　〃　　　20通り
(5)の　　　〃　　　1通り　　　合わせて101通り、つまり101個

（４）f（2005n）≠0　となればよい
それにはnが奇数であることがまず必要である
nが奇数の時、2005nの一の位は5
他の位に１つでも偶数があるとf（2005n）＝0　となるから
一の位の5を含めすべての位が奇数でなければならない
2005nにn＝1,3,5,7,9、・・・・を代入していくと
n＝267の時初めてすべての位が奇数となる　　　　（答え）267

（２）はつい7532と答えてしまいそうです
（４）は電卓でシコシコ計算しました 　　こんなやり方は数学じゃないなと思いながらも楽しい時間でした
　　（うまいやり方があるんだろうなあ～）
　　2005・267＝535335となった時はうれしかったです

解答・その17

（ペンネ－ム：巷の夢）

（1）105＝3×5×7であるので、求める最小数は357である。
（2）210＝2×3×5×7であるので求める最大数は7532・・・・、 ところが2×3＝6であるので5より大きい。因って、7651が求めるものである。
(3)1024＝210であり、これより約数は1,2,4及び8となる。 因って、これらの数字を使用し5桁の数を考えれば良く、試行錯誤から下表の組み合わせとなり、 同じものを取って良い組み合わせの公式を使い計算すると以下の様になる。即ち、101通りである。

使用する数組み合わせ
444441
2444820
2248830
1448830
1288820

（4）2005ｎの各位に0がある場合や、5と偶数がある場合にはｆ（ｆ（2005ｎ））＝0となるので ｎは奇数であると推定される。
その大きさであるが、（2000+5）×（100+90+9）を計算すると、 必ず10万の桁が偶数となる（2000×100＝200000）。 因って、求める奇数は201以上である。
このことから10万の桁数が5以上になれば良く、2005ｎ≧500000からｎ≧251となる。
そこで これ以上の奇数で計算するとｎ＝267で535335と題意を満足する数となる。 即ち求めるものは267である。

解答・その18

（ペンネ－ム：T_Tatekawa）

(1)
35=3x5x7
答え：357

(2)
210=2x3x5x7=1x5x6x7
答え：7651

(3)
1024=210
1x2x8x8x8で 5!/(3! 1! 1!) = 20通り
1x4x4x8x8で 5!/(2! 2! 1!) = 30通り
2x2x4x8x8で 30通り
2x4x4x4x8で 20通り
4x4x4x4x4で 1通り
答え：101通り

(4)
2005n の下一桁は 0 か 5 である．
f(f(2005n)) を考える場合，2005n の下一桁は 5 であり， かつ他の桁の数字は奇数でなければならない． そうでないと，f(2005n) で 0 を含むか，5と偶数を同時に 含む事になるからである． つまり，n は奇数である．
2 は何倍しても偶数なので，千の位を奇数にするには 5 の倍数で 千の位が奇数になるものを考える必要がある．
最小の n は n=200 (2005n=401000)．
ただし n が 200以上249以下だと，十万の位が4になるので不適．
n=250 だと 2005n=501250．
百の位の偶数を奇数に変えるには，n が 260以上．
また，同時に一万の位を奇数に変えるには，nが265以上．
n=265 だと 2005n=531325.
n=267 だと 2005n=535335．
f(535335)=5x3x5x3x3x5=3375
なので，
f(3375)=3x3x7x5=315
なので，条件を満たす．
よって最小の n は n=267．

解答・その19

（ペンネ－ム：夜ふかしのつらいおじさん）

(1)
１０５＝３×５×７
より ｎ＝３５７
つまり ｆ(357)＝１０５

(2)
２１０＝２×３×５×７＝１×５×６×７
より ｎ＝７６５１
つまり ｆ(7651)＝２１０
２１０の素因数は積が９を超えないものがあるので注意が必要です。

(3)
１０２４＝２×２×２×２×２×２×２×２×２×２
２×２×２＝８ なので３つまで組合すことができます。 (i)８、８、８、２、１を使う場合
同じものを含む場合の順列で考えると
　　　５！/３！×１！×１！＝２０
(ii)８、８、４、４、１を使う場合
　　　５！/２！×２！×１！＝３０
(iii)８、８、４、２、２を使う場合
　　　５！/２！×２！×１！＝３０
(iv)８、４、４、４、２を使う場合
　　　５！/３！×１！×１！＝２０
(v)４、４、４、４、４を使う場合
　　　１
以上より１０１通り。

(4)
ｆ(ｆ(2005ｎ))について
積2005ｎのどこかの位に「０」があると、ｆ(2005ｎ)＝０です。
積2005ｎのどこの位にも「０」がなければ、ｆ(2005ｎ)≠０です。
積2005ｎのどこかの位に「偶数の数字」があると、ｆ(2005ｎ)の下１桁は０です。
だから、そのときｆ(ｆ(2005ｎ)）＝０です。
積2005ｎのすべての位が「奇数の数字」であれば、ｆ(ｆ(2005ｎ))≠０です。
(i)ｆ(2005ｎ)は、ｎが偶数のとき下１桁は０なので０になります。
　だから、ｎは奇数でなければなりません。
(ii)１９までの奇数は、積の百の位が０なのでだめです。
(iii)１９９までの奇数は、積の千の位が必ず偶数になりだめです。
(iv)２０１から２４９までの奇数は、積の十万の位が４となりだめです。
(v)２５１から２５９までの奇数は、百の位が２となりだめです。



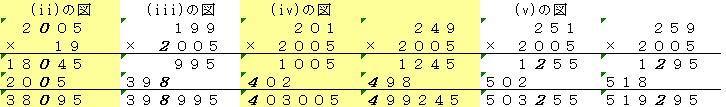
ここから先は１個ずつ調べます。
　2005×261＝ 523305
　2005×263＝ 527315
　2005×265＝ 531325
　2005×267＝ 535335 　すべての位の数字が奇数になりました。
だから、ｎ＝２６７です。

「なお、f(f(2005n))の最小値は、
　　　ｆ(f(2005×55417013023))＝ｆ(f(111111111111115))＝f(5)＝5
のようです。また、次に小さい値は、
　　　f(f(2005×5583))＝f(f(11193915))＝f(1215)＝10
のようです。

解答・その20

（ペンネ－ム：浜田　明巳）

(1) 357
(2) 7651
(3) 101個
(4) 267

Option Explicit
Sub Macro1()
    Sheets("Sheet1").Select
    Range("A1").Select
    Dim n As Long
    Dim deta As Integer
    Cells(1, 1).Value = 1
    deta = 0
    n = 100
    While deta = 0 And n < 1000
      If f(n) = 105 Then
        deta = 1
        Cells(1, 2).Value = n
      Else
        n = n + 1
      End If
    Wend
    '
    Cells(2, 1).Value = 2
    deta = 0
    n = 9999
    While deta = 0 And n >= 1000
      If f(n) = 210 Then
        deta = 1
        Cells(2, 2).Value = n
      Else
        n = n - 1
      End If
    Wend
    '
    Cells(3, 1).Value = 3
    Cells(3, 2).Value = 0
    For n = 10000 To 99999
      If f(n) = 1024 Then
        Cells(3, 2).Value = Cells(3, 2).Value + 1
        Cells(3, Cells(3, 2).Value + 2).Value = n
      End If
    Next n
    '
    Cells(4, 1).Value = 4
    deta = 0
    n = 1
    While deta = 0
      If f(f(2005 * n)) > 0 Then
        deta = 1
        Cells(4, 2).Value = n
      Else
        n = n + 1
      End If
    Wend
End Sub
Private Function f(ByVal n As Long) As Long
    Dim nn As String
    Dim j As Integer
    nn = Right(Str(n), Len(Str(n)) - 1)
    f = 1
    For j = 1 To Len(nn)
      f = f * Val(Mid(nn, j, 1))
    Next j
End Function


正解者

バルタン星人 スモークマン のっこん
teki オヤジ 巷の夢
こまったコ 夜ふかしのつらいおじさん 長崎島原　かがみ
転位反応 杖のおじさん T_Tatekawa
浜田　明巳 Ukiki_masamasa 三角定規
mariki テレスとアリス 赤影
G3 迷子の雄猫

コメント

(1)は素直に答えられますが、(2)はつい、「7532」と答えてしまいそうですね。
(4)では、2005n（これは2005×nです。）に対して、関数ｆを２回作用させているところに 注意が必要です。2005は、５の倍数であることから、「０」を避けるために、 偶数を排除しなければなりません。 つまり、2005nの各桁がすべて奇数でなければなりません。 この条件を満たすｎを探していきます。ｎももちろん奇数です。 Excelを使って探す他に、工夫して探してくださった解答もありますね。

top