MONDAI14

Weekend Mathematics／問題／問題14

１４．表面積の問題

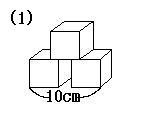
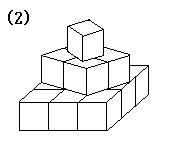
下の図にある立法体の表面積を求めよ。ただし、立方体はどれも１辺の長さが４cmとします。

問題の出典

立正中学校'93入試

パズルより面白い中学入試の算数

ピ－タ－・フランクル

講談社

答えと解説

（１）回答・その１

（ペンネ－ム：ＪＲ東日本二泊三日湯けむり温泉旅行）

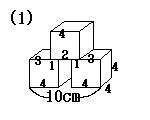
正方形がしっかり出ているのが１５個
３×４の四角形が２つ
２×４の四角形が１つなので、
４^２×１５＋３×４×２＋２×４＝２７２
２７２cm²

（１）回答・その２

（ペンネ－ム：ＢＡＢＹ　ＭＩＮＮＩＥ）

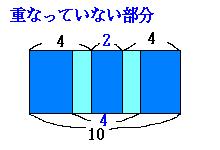
まず、１辺が４の正方形が１５個。
左の図のように、４－２＝２で、重なっているのは、２×４＝８
従って、１６×１５＋１０×４－８＝２７２

（１）回答・その３

（ペンネ－ム：ｅｓ）

立方体３個の表面積は、
４×４×６×３＝２８８
ここから重なった部分の面積をひくと、
２８８－４×１×２×２＝２７２

（１）あれ－っ？

下の立方体の間が１０－（４＋４）＝２なので、
隠れている部分は１。
よって、隠れている部分の面積は１×４×２＝８。
隠れている部分が無いとしてみた時の表面積は、
４×４×６×３＝２８８
これから隠れている部分を引いて、
２８８－８＝２８０

（１）あれ－っ？・コメント

アイディアは「ｅｓ」さんと同じですよね。
ただし、「×２」を忘れてしまっていますね。両面で接しているわけだから、２倍しなくちゃね。

（２）回答・その１

（ペンネ－ム：What･to･do?）

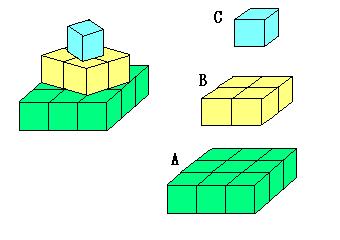
一番下と側面にある正方形の個数は、
４＋８＋１２＋９＝３３
４×４×３３＝５２８
一番下の段の上
１６×９－１６×４＝８０
２段目の上
１６×４－１６＝４８
一番上の段の上
１６
すべてたして、５２８＋８０＋４８＋１６＝６７２

（２）回答・その２

（ペンネ－ム：狐の孔明有るは楢魚の水有るがごとし）

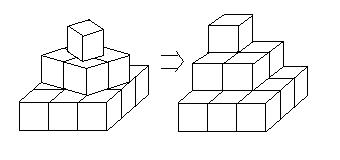
隠れている部分の面積はどこに積み重ねても同じなので、上の図のようにするとわかりやすい。
上の面の面積は１２×１２＝１４４
下の面も同様に１４４
側面は下段が４×１２×４＝１９２
中段が４×８×４＝１２８
上段が４×４×４＝６４
全てたして、１４４＋１４４＋１９２＋１２８＋６４＝６７２

（２）回答・その３

（ペンネ－ム：Ｐ．Ｎ．Ｓｈａｋｅ）

全体の表面積から重なっている面積の２倍を引くことにする。
下段の表面積は
４（縦）×１２（横）×４（個数）＋１２×１２××２＝４８０（平方ｃｍ）
中段；４×８×４＋８×８×２＝２５６（平方ｃｍ）
上段；９６（平方ｃｍ）

下段と中段の重なっている部分の面積；８×８＝６４（平方ｃｍ）
中段と上段の重なっている部分の面積；４×４＝１６（平方ｃｍ）

よって求める面積は
４８０＋２５６＋９６－２×（６４＋１６）＝６７２（平方ｃｍ）

Ａ．６７２平方ｃｍ

回答・特別編

（ペンネ－ム：↑MEより上にいる人！次回は抜くゾ）

こんにちは－。長い間ごぶさたしていました。（注１）覚えていますか？「ハンド君」です。

こんにちは－。本当に久しぶりの登場です。前回はチョコレ－ト、どうもありがとうございました。（注２）おいしくいただきましたよ！助手の「手のひら君」です。

さてさて、今回は図形の問題だ。今回もまた、二人でやり方を考えながら解いていこうじゃないか、「手のひら君」。

ええっ－！ぼく、図形の問題って凄く苦手なんです。今回は「ハンド君」にすべてお任せしますからよろしく。

おいおい、困るよ。手伝ってくれよ。

グゥ・・・。（いびきの音）

・・・え？マジ？寝てんの・・・？－弱ったなぁ。それじゃあ今回は。「手のひら君」の直感に頼らず、僕の計算力だけで問題を解いてみよう。

ちなみに、（２）の図形の２段目以降にずれが生じているのは、このワ－プロの機能が悪いせいです。問題は、プリントのものと同じものです。（注３）

え？何？起きたの、「手のひら君」？

今のは寝言、寝言・・・グゥ・・・。

・・・・・・・。

それでは、（１）の問題から解いていきます。

太線＝４－（１０－４×２）÷２＝１
これだけのことがわかっていれば、この問題は解けるんじゃないかな。答えを導くための式は、
全体の表面積－重なっている部分の面積×２
∴４×４×１８－１×４×２×２＝２８８－１６＝２７２
ほら。できたでしょ。
つづいて（２）もやってみたいと思います。

一つ一つを分解すると、こんな感じになります。
ここで、一段目をＡ、二段目をＢ、三段目をＣとおき、それぞれの表面積を求めてみましょう。
Ａ＝４×４×３０＝４８０
Ｂ＝４×４×１６＝２５６
Ｃ＝４×４×６＝９６
∴Ａ＋Ｂ＋Ｃ＝４８０＋２５６＋９６＝８３２
これで、全体の表面積が出たわけです。
しかしＢの底辺と、Ｃの底辺は重なって見えないため、その分を全体から引かなくてはなりません。重なっている部分の面積は、
Ｂの底辺＝４×４×４＝６４
Ｃの底辺＝４×４×１＝１６
∴重なっている部分の面積は、
６４×２＋１６×２＝１２８＋３２＝１６０
これを全体から引けば、（２）の表面積が出るわけです。
８３２－１６０＝６７２

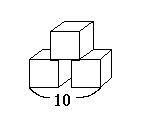
ふぅ－。解けました解けました。２問とも無事に、済ませましたよ。

でも答えがあっているかどうかは、まだ分からないよ。長い間かかって作った図形も、計算ミスの為水のアワ－！なんてことも有る得るし。

うう・・・。「手のひら君」。これも寝言かい？・・・たいした度胸してるねぇ、君。なんにもしないでそんなこと言える立場だと思ってんの？

あははははははははは！反省して、徹底的に見直しします！

よろしい。

回答・特別編・コメント

注１：以前にも「ハンド君」と「手のひら君」の会話形式のレポ－トをもらったことがあるのです。
注２：その時にチョコレ－トをプレゼントしたのです。
注３：ワ－プロでかかれたレポ－トです。ちゃんと図もかかれていました。残念ながら再現できないので、今回の図は私が作り直しました。

正解者（ペンネ－ム）

せっきー

Hungry Bear

板垣央

ＢＲＡＩＮＭＡＮＩＡ

Ｐ．Ｎ．Ｓｈａｋｅ

凡人

What･to･do?

↑MEより上にいる人！次回は抜くゾ

ＢＡＢＹ　ＭＩＮＮＩＥ

ＪＲ東日本二泊三日湯けむり温泉旅行

コレクトコ－ルは１０６番！

狐の孔明有るは楢魚の水有るがごとし

ｅｓ

戻る