１３８．カード折りたたみの問題
数字の書いてある同じ大きさの正方形のカードを何枚かつなぎます。
それを机の上に置き、
１のカードを動かさないようにして、他のカードを上へ折り重ねていきます。
つないだところ以外は、カードを曲げたり、折ったりできません。
また、一度折ったところは開かないことにします。
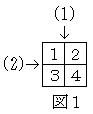
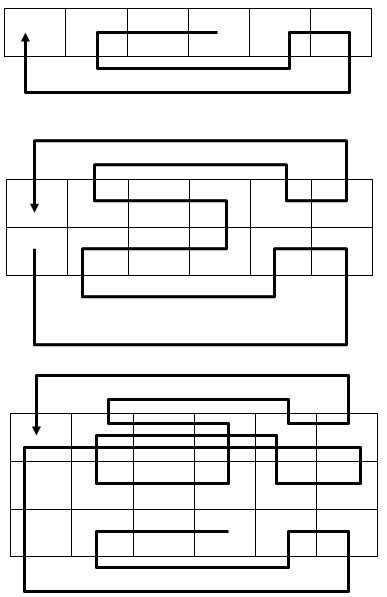
例えば、右の図１のようにつなぎ、
(1)、(2)の順に折るとカードは上から順に
３→４→２→１
となります。
次のそれぞれの場合について、カードの番号を上から順に答えてください。
ただし、一番下は１となります。
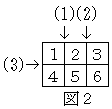
(1)下の図２にように６枚のカードをつなぎ、(1)、(2)、(3)の順に折るとき。
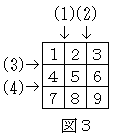
(2)下の図３のように９枚のカードをつなぎ、(1)、(2)、(3)、(4)の順に折るとき。
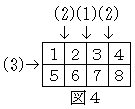
(3)下の図４のように８枚のカードをつなぎ、(1)、(2)、(3)の順に折るとき。
問題の出典
センスのよい脳をつくる 大人の算数パズル
河瀬 厚 著
自由国民社
学習院女子中等科 2006年
答えと解説
解答・その1
（ペンネ−ム：テレスとアリス）
(1) ４→５→６→３→２→１
(2) ９→８→７→４→５→６→３→２→１
(3) ５→８→７→６→２→３→４→１
以上です。
解答・その2
（ペンネ−ム：やなせ）
問い１
４．５．６．３．２．１
問い２
９．８．７．４．５．６．３．２．１
問い３
５．８．７．６．２．３．４．１
良く解らないので実際に紙に数字を書いて折ってみました。
解答・その3
（ペンネ−ム：teki）
１ ４５６３２１
２ ９８７４５６３２１
３ ５８７６２３４１
１及び２のような折り方では、１から順に全てのマス目を１回ずつ通る通り方に帰着します。
３は少し複雑で、これは実際やったほうが早そうです。
解答・その4
（ペンネ−ム：こまったコ）
A. 1
(1)は谷折(上段:1の上に2; 下段:4の上に5)。
(2)は山折(上段:2の上に3; 下段:5の上に6)。
(3)は上に谷折(下から:下段の1, 2, 3 の上に上段の6, 5, 4)
まとめると4→5→6→3→2→1
A. 2
(1)は谷折(上段:1の上に2; 中段:4の上に5;下段:7の上に8)。
(2)は山折(上段:2の上に3; 中段:5の上に6;下段:8の上に9)。
(3)は上に谷折(下から:下段の1, 2, 3 の上に中段の6, 5, 4)。
(3)は下に山折(下から:中段の6, 5, 4 の上に上段の7, 8, 9)。
まとめると9→8→7→4→5→6→3→2→1
A. 3
(1)は谷折(1の上に4, 2の上に3, 5の上に8, 6の上に7)。
(2)は谷折(4の上に3,2 8の上に7, 6)。
(3)は谷折(2の上に6,7,8,5)。
まとめると5→8→7→6→2→3→4→1
解答・その5
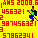（ペンネ−ム：杖のおじさん）
問題１、 ４→ ５→ ６→ ３→ ２→ １
問題２、 ９→ ８→ ７→ ４→ ５→ ６→ ３→ ２→ １
問題３、 ５→ ７→ ８→ ６→ ２→ ３→ ４→ １
条件は１を動かさないように固定するので注意する。折り返すと上になったカードは
下になりますので順番は逆になります。
上のカードの番号は下になり下のカードの番号は上になります。従って次のようになります。
（ ）内は折り返した回数、［ ］内は下からのカードの順番です。
問題１
（１） （２） （３）
[1][2][2] [1][2][3] [1][2][3][4][5][6]
１→２，３ １→２→３ １→２→３→４→５→６
４→５，６ ４→５→６
従って答えは ６→５→４→３→２→１
問題２
（１） （２） （３）
[1][2][2] [1][2][3] [1][2][3][4][4][5][5][6][6]
１→２、３ １→２→３ １→２→３ ６、９ ５、８ ４、７
４→５、６ ４→５→６
７→８，９ ７→８→９
（４）
[1][2][3][4][5][6][7][8][9]
１→２→３→６→５→４→７→８→９
従って答えは ９→８→７→４→５→６→３→２→１
問題３
（１） （２） （３）
[1] [2][1][2] [1][2][3][4] [1][2][3][4]
１→４ ２→３ １→４→３→２ ５→７→８→６
５→７ ６→８
（４）
[1][2][3][4][5][6][7][8]
１→４→３→２→６→８→７→５
従って答えは ５→７→８→６→２→３→４→１
解答・その6
（ペンネ−ム：転位反応）
１)
（３）のように、カードの上下に沿って折りたたむと順序が反転することに注意すれば良い。
２)
上記 1) の結果に操作（４）を加えて考えれば良い。
カードの上下に沿って二度折りたたむと順序の反転は無いことに注意する。
３)
操作（１）(２)によって、カード１,２,３,４の順序を求め、
それに４を加えれば、カード５,６,７,８の順序が容易に求められる。
解答・その7
（ペンネ−ム：のっこん）
（１）１と（１）の折り軸に関して対称なのは２
２と（２）の折り軸に関して対称なのは３
１行目は下から１→２→３
２行目は下から４→５→６
３と（３）の折り軸に関して対称なのは６
よって上から４→５→６→３→２→１
（２）１と（１）の折り軸に関して対称なのは２
２と（２）の折り軸に関して対称なのは３
１行目は下から１→２→３
２行目は下から４→５→６
３行目は下から７→８→９
３と（３）の折り軸に関して対称なのは６
４と（４）の折り軸に関して対称なのは７
よって上から９→８→７→４→５→６→３→２→１
（３）１と（１）の折り軸に関して対称なのは４
４と（２）の折り軸に関して対称なのは３
１行目は下から１→４→３→２
２行目は下から５→８→７→６
２と（３）の折り軸に関して対称なのは６
よって上から５→８→７→６→２→３→４→１
解答・その8
（ペンネ−ム：オヤジ）
数を、表示して考える
（１） ∴ ４→５→６→３→２→１
１，２，３ ４，５，６ (1)を折る (2) を折る (3) を折る ３，２→１ ３→２→１ ４→５→６→３→２→１ ６，５→４ ６→５→４
（２） ∴ ９→８→７→４→５→６→３→２→１
１，２，３ ４，５，６ ７，８，９ (1) を折る (2) を折る (3) を折る ３ ，２→１ ３→２→１ ７→８→９ ６ ，５→４ ６→５→４ ４→５→６→３→２→１ ９ ，８→７ ９→８→７ (4) を折る ９→８→７→４→５→６→３→２→１
（３） ∴ ５→８→７→６→２→３→４→１
１，２，３，４ ５，６，７，８ (1) を折る (2) を折る (3) を折る ４→１，３→２ ２→３→４→１ ５→８→７→６→２→３→４→１ ８→５，７→６ ６→７→８→５
解答・その9
（ペンネ−ム：迷子の雄猫）
（１） ４５６３２１
（２） ９８７４５６３２１
（３） ５８７６２３４１
このように順々に追いかけてときました。問題（２）の折り方（３）で「７８９」の上
下がひっくり返るところがミソかなと思いました。
１ １２ １２３ １２３６５４ ２ ３ ３ ４ ４５ ４５６ ５ ６ ６
解答・その10
（ペンネ−ム：巷の夢）
（1） 4→5→6→3→2→1
（2） 9→8→7→4→5→6→3→2→1
（3）5→8→7→6→2→3→4→1
問題（1）と（2）についての 規則を図示してみました。綺麗な流れになりますね。要は1から最大 数の所まで線を引いていき、その逆が現われる数字の順番となります。
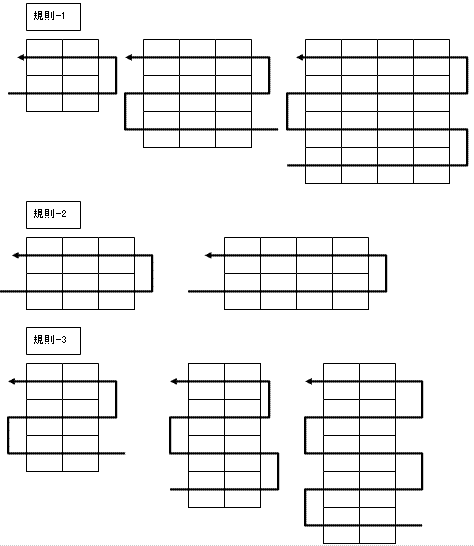
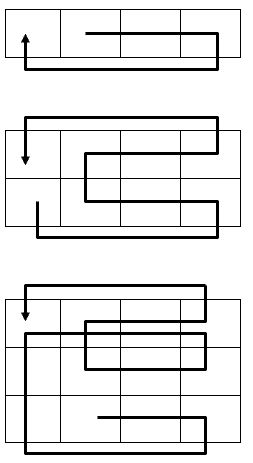
問題（3）についての規則を図示してみました。
解答・その11
（ペンネ−ム：スモークマン）
1の上に何が来るか、それが来たら1とくっつくのでもう動かないから、今度はその上
に何がくるか、それも同様にもう動かないので、、、の繰り返しで。。。
1-2-3-
その下は、4-5-6 だったので、上に逆順で続く。
つまり、1-2-3-6-5-4
上からだと、、、4-5-6-3-2-1
(2)同様に考えて、、、
1-2-3、その下は、4-5-6、その下は、7-8-9
4に続くのは7なので、、、1-2-3-6-5-4-7-8-9
上からだと、、、9-8-7-4-5-6-3-2-1
(3)同様に、1-4-3-2
その下は、5-8-7-6
なので、、、1-4-3-2-6-7-8-5
上からだと、、、5-8-7-6-2-3-4-1
でいいのかな？ ^^
多分置換操作のようなことを駆使するんでしょうね...^^;
解答・その12
（ペンネ−ム：T_Tatekawa）
(1) 1回目の折りたたみで 1 の上に 2 が来ます．
2回目の折りたたみで 2 の上に 3 が来ます．
1-2-3 と 4-5-6 の重なりがあるところで，3回目の折りたたみを
すると，3 の上に 6-5-4 と来るので，上から順に見ていくと
4→5→6→3→2→1
です．
(2) 2回目までは (1) と同じです．
この時点で 1-2-3, 4-5-6, 7-8-9 とあります．
3回目の折りたたみで 3 の上に 6-5-4 が来て，4回目の折りたたみで
4 の上に 7-8-9 が来ます．上から順に見ていくと，
9→8→7→4→5→6→3→2→1
です．
(3) 1 回目と 2 回目の折りたたみで，
1-4-3-2 と 5-8-7-6 という重なりがあります．
3回目の折りたたみは 2 と 6 を重ねるので，上から順に見ていくと，
5→8→7→6→2→3→4→1
です．
解答・その13
（ペンネ−ム：夜ふかしのつらいおじさん）
図１で (1)、(2)の順に折るとカードは上から順に
３→４→２→１ ・・・ （あ）
(1)
図２で、「３」「６」がないとします。
すると折り方は図１のときと同じです。
１：１、２：２、３：４、４：５と対応します。
上の（あ）に対応する数を代入すると、
４→５→２→１
次に「３」「６」を考えます。
折り方を考えると
「５」と「２」に挟まれて「６」が上にくることが分かるので
解答は、
４→５→(６→３)→２→１
(2)
図３で、「７」「８」「９」がないとします。
すると折り方は図２のときと同じです。
４→５→６→３→２→１
次に「７」「８」「９」を考えます。
折り方を考えると
「７」「８」「９」とつながって「９」が最上位にくることが分かるので
解答は、
(９→８→７)→４→５→６→３→２→１
(3)
図４で、まず上の並びの「１」「２」「３」「４」だけを考えます。
すると上から
２→３→４→１
次に下の並びの「５」「６」「７」「８」を考えます。
上の並びの上に「５」「８」「７」「６」とつながって
「５」が最上位にくるので
(５→８→７→６)→２→３→４→１
解答・その14
（ペンネ−ム：長崎島原 かがみ）
(例)この場合は、１の上に２が、３の上に４が来た後、再度の折りたたみによって、
３と４の上下が入れ替わる。
したがって、３→４→２→１となる。
(問題１)この場合も、(例)と同様に、４→５→６→３→２→１となる。
(問題１')この場合も、(例)と同様に、
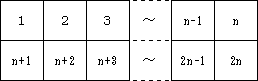
n+1→n+2→n+3→・・・→2n-1→n→n-1→・・・→３→２→１となる。
(問題２)この場合は、偶数行目だけが入れ替わって、
９→８→７→４→５→６→３→２→１となる。
(問題２')この場合は、偶数行目だけが入れ替わって、
９→８→７→４→５→６→３→２→１となる。
(問題３)この場合は、まず１の上に４、２の上に３、５の上に８、６の上に７が来る。
それを、縦に折り返すと、１４の上に３２が来て、５８の上に７６が来る。
それを、横に折り返すので、６７８５が上下入れ替わって、５８７６が来る。
したがって、５→８→７→６→２→３→４→１となる。
マス目がもっとたくさんの場合に、折り返し方によって、
どんな番号順に並ぶのかの規則を見つけるのは、おもしろいと思います。
解答・その15
（ペンネ−ム：三角定規）
［１］<図1-1> を(1)(2)で折ると <図1-2> となり，
さらに(3)で折りたたむと下段の ６５４が逆転して、
上から ４，５，６，３，２，１ <図1-3> となる。
［２］<図2-1> を(1)(2)で折ると <図2-2> となり，
さらに(3)(4)で折りたたむと中段の ６５４が逆転して、
上から ９，８，７，４，５，６，３，２，１ <図2-3> となる。
［３］<図3-1> を(1)で折ると <図3-2> となり，
さらに(2)で折りたたむと <図3-3> となる。
最後に(3)で折りたたむと下段の６７８５が逆転して，
上から ５，８，７，６，２，３，４，１ <図3-3> となる。
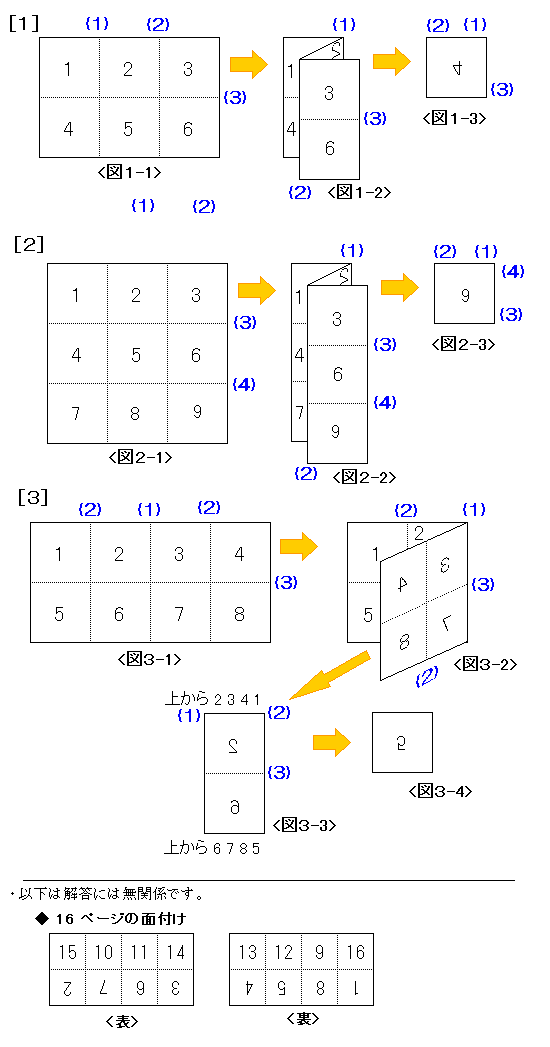
これは印刷製本の過程が題材になっている問題ですね。
ページ数がそう多くない雑誌などを作るときって，１６ページ単位で印刷しますね。
いまは，全部コンピューターでやるのでしょうが，昔本郷の印刷所で，組版木枠をミリ以下の単位で位置を調整しながら並べていたのを見たことがあります。
印刷された大きな紙を折って折って，本にした後３方を裁断してできあがり
解答・その16
（ペンネ−ム：ＳＯＵ）
高さを数値で表していきます。
ひっくり返る部分が基本的に高くなるので、その際数を加えていきます。
ひっくり返る部分の厚みが2以上の場合は、ひっくり返る前と後で高さの順番が逆になるので、
より低いものほど高くなるように、数を入れかえ、更にを加えます。
問題(1)
(1)適用後
| 0 | 1 | 1 |
|---|---|---|
| 0 | 1 | 1 |
ひっくり返る部分を青くしました。 ひっくり返る前は厚み1なので、ひっくり返った後の4マスは同じ高さなので、同じ数を入れます。
(2)適用後
| 0 | 1 | 1+2 |
|---|---|---|
| 0 | 1 | 1+2 |
次にひっくり返る2マスも、厚み1なので同じ数字を入れます。 前にひっくり返った2列目より高くなるので、区別のためひとつ大きな位の数字にします。
(3)適用後
| 0 | 1 | 1+2 |
|---|---|---|
| 1+2+4 | 1+4 | 4 |
最後は、ひっくり返る部分の厚みが1でないので、(2)適用後の2行目の数字を、 対称的に入れかえ、4を加えます。
より数字の大きい方がより高い位置にあるということなので、答えは
| 6 | 5 | 4 |
|---|---|---|
| 1 | 2 | 3 |
問題(2)
(1)適用後
| 0 | 1 | 1 |
|---|---|---|
| 0 | 1 | 1 |
| 0 | 1 | 1 |
(2)適用後
| 0 | 1 | 1+2 |
|---|---|---|
| 0 | 1 | 1+2 |
| 0 | 1 | 1+2 |
(3)適用後
| 0 | 1 | 1+2 |
|---|---|---|
| 1+2+4 | 1+4 | 4 |
| 1+2+4 | 1+4 | 4 |
ひっくり返る部分の厚みが1でないので、2行目、3行目の高さの順を入れ替えつつ4を加えます。
(4)適用後
| 0 | 1 | 1+2 |
|---|---|---|
| 1+2+4 | 1+4 | 4 |
| 4+8 | 1+4+8 | 1+2+4+8 |
同じく、厚みが1でないので、3行目を入れ替えつつ8を加えます。
以上より答えは
| 9 | 8 | 7 |
|---|---|---|
| 4 | 5 | 6 |
| 3 | 2 | 1 |
問題(3)
(1)適用後
| 0 | 0 | 1 | 1 |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
(2)適用後
| 0 | 1+2 | 2 | 1 |
|---|---|---|---|
| 0 | 1+2 | 2 | 1 |
(3)適用後
| 0 | 1+2 | 2 | 1 |
|---|---|---|---|
| 1+2+4 | 4 | 1+4 | 2+4 |
2行目の、より低いものがより高くなるように数を入れかえ、4を加えます。
以上から答えは、
| 8 | 5 | 6 | 7 |
|---|---|---|---|
| 1 | 4 | 3 | 2 |
解答・その17
（ペンネ−ム：バルタン星人）
素直に順番を考えました。
１）４５６３２１
２）９８７４５６３２１
３）５８７６２３４１
正解者
| 長崎島原 かがみ | スモークマン | 迷子の雄猫 |
| やなせ | 杖のおじさん | teki |
| 巷の夢 | こまったコ | のっこん |
| 転位反応 | 夜ふかしのつらいおじさん | T_Tatekawa |
| 三角定規 | テレスとアリス | ＳＯＵ |
| オヤジ | バルタン星人 |
コメント
三角定規さんのご指摘にありますが、
印刷製本の仕方に発展するとは驚きです。
いただいた解答の中で、ＳＯＵさんの解答は、
書かれた数字を追うのではなく、その面の位置を考察しているという
点で、大変ユニークだなと思いました。
top