侾俁俈丏椫僑儉偺栤戣
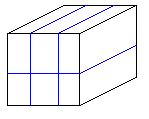
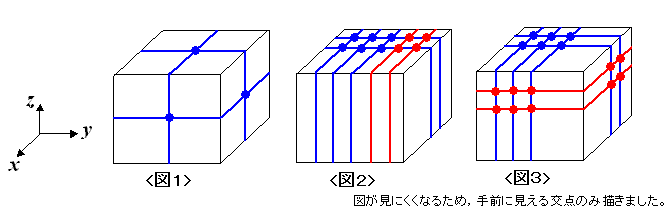
師偺傛偆偵丄椫僑儉傪棫曽懱偺敔偵偐偗傑偡丅
丂丒椫僑儉偼棫曽懱偺曈偲捈妏偵岎傢傞
丂丒岦偒偑摨偠椫僑儉偼廳側傜側偄
偐偗偨椫僑儉偳偆偟偺岎揰偺屄悢偵偮偄偰峫偊傑偡丅
椺偊偽丄俁杮偺椫僑儉傪塃偺恾偺傛偆偵偐偗偨偲偒丄岎揰偼係屄偱偡丅
師偺栤偄偵摎偊側偝偄丅
(1)丂俁杮偺椫僑儉傪偐偗傞偲偒丄岎揰偼嵟傕懡偔偰壗屄偱偒傑偡偐丅
(2)丂俆杮偺椫僑儉傪偐偗偨偲偙傠丄岎揰偼侾俀屄偁傝傑偟偨丅偝傜偵俁杮偺椫僑儉傪偐偗偨傜丄
岎揰偼慡晹偱壗屄偵側傝傑偡偑丅嵟傕懡偄応崌傪丄嵟傕彮側偄応崌偺岎揰偺屄悢傪摎偊側偝偄丅
(3)丂侾侽侽杮偺椫僑儉傪偐偗傞偲偒丄岎揰偼嵟傕懡偔偰壗屄偱偒傑偡偐丅
栤戣偺弌揟
僙儞僗偺傛偄擼傪偮偔傞丂戝恖偺嶼悢僷僘儖
壨悾丂岤丂挊
帺桼崙柉幮
拀攇戝妛晬懏嬵応拞妛峑丂2006擭
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗偙傑偭偨僐乯
(1) 帺暘偺恀惓柺偵棫曽懱偑偁傞偲偟偰丄廲曽岦丄墶曽岦丄懁柺偵偦傟偧傟1杮偢偮偐偗偰6屄丅
(2) 帺暘偺恀惓柺偵棫曽懱偑偁傞偲偟偰丄廲曽岦偵3杮丄墶曽岦2杮偐偗傟偽岎揰偼12屄丅
岎揰傪傕偭偲傕懡偔偡傞偵偼懁柺曽岦偵3杮偐偗傞丅岎揰偼12+10亊3=42屄丅
岎揰傪傕偭偲傕彮側偔偡傞偵偼3杮偐偐偭偰偄傞廲曽岦偵3杮偲傕偐偗傞丅岎揰偼24屄丅
(3)帺暘偺恀惓柺偵棫曽懱偑偁傞偲偟偰丄廲曽岦偵33杮丄墶曽岦偵33杮丄懁柺偵34杮偐偗傞丅
岎揰偼6666屄丅
夝摎丒偦偺2
乮儁儞僱亅儉丗挿嶈搰尨丂偐偑傒乯
乮侾乯亂恾侾亃偺傛偆偵慡曽岦偵椫僑儉傪偐偗偨応崌丄岎揰悢偑嵟戝偲側傞丅
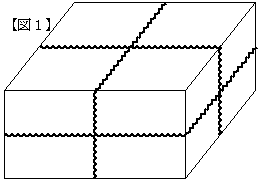
傛偭偰丄嵟戝岎揰悢丂俇屄
乮俀乯俆杮偱岎揰偑侾俀屄偱偒傞偺偼丄亂恾俀亃偺応崌偱偁傞丅
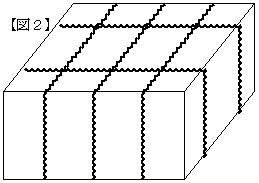
偙傟偵俁杮捛壛偡傞丅
(i)丂嵟掅岎揰悢偺応崌
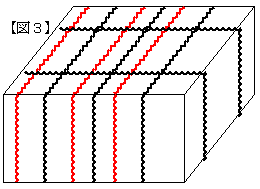
亂恾俁亃偺傛偆偵丄岎揰偼俁杮亊係屄亖侾俀屄憹壛偡傞偐傜丄侾俀亄侾俀亖俀係屄
傛偭偰丄嵟掅岎揰悢偼丂俀係屄
(ii)丂嵟戝岎揰悢偺応崌
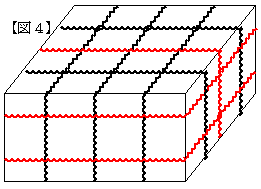
亂恾係亃偺傛偆偵丄岎揰偼俇屄亊係亄俁屄亊俀亖俁侽屄憹壛偡傞偐傜丄
侾俀亄俁侽亖係俀屄
傛偭偰丄嵟戝岎揰悢偼丂係俀屄
乮俁乯椫僑儉傪慡曽岦乮俁曽岦乯偵偐偗傞応崌偑嵟戝偲側傞偺偱丄椫僑儉偺杮悢偑
俁丄俇丄俋丄侾俀丄丒丒丒偺応崌偑嵟戝偲側傞丅
値傪帺慠悢偲偟偰丄
椫僑儉偑俁値杮偺応崌偺嵟戝岎揰悢傪M偲偡傞偲丄
M亖俀値亊俁値亖俇値俀偲側傞丅
椫僑儉偑俋俋杮偡側傢偪値亖俁俁偺偲偒丄M亖俇亊俁俁俀 偲側傞丅
偙傟偵侾杮偩偗捛壛偡傟偽侾侽侽杮偵側傞偺偱丄偳偺曽岦偵椫僑儉傪偐偗偰傕
俁俁屄亊係柺暘偩偗岎揰偑憹壛偡傞丅
傛偭偰丄岎揰偼丄俇亊俁俁俀亄俁俁亊係亖俇俆俁係亄侾俁俀亖俇俇俇俇屄偵側傞丅
嵟戝岎揰悢偼丂俇俇俇俇屄
夝摎丒偦偺3
乮儁儞僱亅儉丗僥儗僗偲傾儕僗乯
(1) 俁杮偺椫僑儉傪偐偗傞偲偒丄岎揰偑嵟傕懡偄偺偼丄
摨偠岦偒偵偐偗偢丄俁杮偲傕偍屳偄偵岎傢傞傛偵偐偗偨偲偒偱偡丅
岎揰偼俇屄偱偡丅
(2) 俆杮偺椫僑儉偱岎揰偑侾俀屄側偺偱丄
俁杮偑摨偠岦偒偱丄偦傟偵捈妏偵俀杮偐偗傜傟偰偄傞偲峫偊傑偡丅
岎揰偑嵟傕彮側偄偺偼丄
丂丂丂摨偠岦偒偺俁杮偲摨偠岦偒偵俁杮偐偗偨偲偒偱岎揰偼俀係屄偱偡丅
岎揰偑嵟傕懡偄偺偼丄
丂丂丂摨偠岦偒偺俁杮偍傛傃俀杮偵丄捈妏偵岎傢傞傛偆偵偐偗偨偲偒偱丄岎揰偼係俀屄偱偡丅
(3) 摨偠岦偒偵俁俁杮偐偗偰丄偦傟偵捈妏偵俁俁杮偐偗偰丄
偝傜偵捈妏偵俁係杮偐偗傞偲偒偑丄岎揰偑嵟傕懡偔側傝傑偡丅岎揰偼俇俇俇俇屄偱偡丅
夝摎丒偦偺4
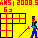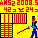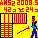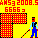 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊
乮侾乯俇屄
乮俀乯嵟傕懡偄傕偺丂係俀屄丄嵟傕彮側偄傕偺丂俀係屄
乮俁乯俇俇俇俇屄
(1)俁亐俁亖侾
侾亊侾亊俀亄侾亊侾亊係亖俇屄
(2)丂丂俆亄俁亖俉
嵟傕懡偄傕偺丂丂俉亐俁亖俀梋傝俀
俁亊俁亊俀亄俁亊俀亊係亖侾俉亄俀係亖係俀屄
嵟傕彮側偄傕偺傪寁嶼偡傞偵摉偨偭偰俆杮偺椫僑儉偱岎揰偑侾俀屄偁傞帠偑
慜採偵側偭偰偄傑偡偺偱俀杮偼婛偵墶曽岦偵妡偗傜傟偰偄傞偙偲偑暘傝傑偡丅
廬偭偰廲曽岦偵巆傝偺俇杮傪妡偗傞偙偲偵側傞偺偱師偺寁嶼幃偵側傝傑偡丅
嵟傕彮側偄傕偺偼丂丂俇亊俀亊俀亖俀係屄
(3) 侾侽侽亐俁亖俁俁梋傝侾
俁俁亊俁俁亊俀亄俁俁亊俁係亊係亖俀侾俈俉亄係係俉俉亖俇俇俇俇屄
夝摎丒偦偺5
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
乮侾乯俇
乮俀乯嵟戝係俀丄嵟彫俀係
乮俁乯俇俇俇俇
椫僑儉偺妡偗曽偼俁庬椶丅偦傟偧傟俙丆俛丆俠杮妡偗傞偲偡傞偲
岎揰偼俀乮俙俛亄俙俠亄俛俠乯
乮侾乯嵟戝偼俙亖俛亖俠亖侾偺帪
乮俀乯侾俀杮偵側傞偺偼丄乮俙丆俛丆俠乯亖(俁丄俀丄侽)偺帪
嵟戝偼(俁丆俁丆俀乯偺帪偱係俀
嵟彫偼乮俇丆俀丆侽乯偺帪偱俀係
乮俁乯嵟戝偼乮俁係丆俁俁丆俁俁乯偺帪
俀亊俁俁亊乮俁俁亄俁係亄俁係乯亖俀亊俁俁亊侾侽侾亖俇俇俇俇
夝摎丒偦偺6
乮儁儞僱亅儉丗揮埵斀墳乯
(侾)俇屄
棫曽懱偵懳偡傞椫僑儉偺妡偗曽偼丄柺倎亅倐丆柺倎亅們丄柺倐亅們偺俁捠傝丅
俀杮偺椫僑儉傪堎側傞柺偵妡偗傞偲俀屄偺岎揰偑偱偒傞偑丄摨堦偺柺偵妡偗傞偲岎揰偼偱偒側偄丅
傛偭偰丄俁杮偺椫僑儉傪俁偮偺堎側傞柺偵妡偗偨応崌丄嵟傕懡偔偺岎揰偑偱偒傞丅
侾偮偺柺偵侾偮偺岎揰偑偱偒傞偺偱丄媮傔傞岎揰偺悢偼俇屄丅
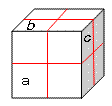
(俀)嵟懡係俀屄丄丂嵟彮俀係屄
俆杮偺椫僑儉傪妡偗偰丄岎揰偑侾俀屄偺忬懺傪壓恾偵帵偟偨丅
忋婰乮侾乯偺寢壥傪婎偵峫偊偲丄
岎揰偺憹壛傪嵟彮偵偡傞偵偼丄柺倎亅們偵俁杮偺椫僑儉傪妡偗傞偲椙偄丅
岎揰偺憹壛偼丄俀亊俁亊俀亖侾俀側偺偱丄岎揰偼慡晹偱俀係屄丅
堦曽丄岎揰偺憹壛傪嵟懡偵偡傞偵偼丄柺倐亅們偵椫僑儉傪俁杮妡偗傞丅
岎揰偺憹壛偼丄俁亊俁亊俀亄俀亊俁亊俀亖俁侽屄
傛偭偰丄岎揰偺悢偼慡晹偱係俀屄
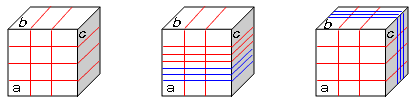
(俁)俇俇俇俇屄
侾侽侽亖俁俁亊俁亄侾側偺偱丄侾偮偺柺偵俁俁杮偺椫僑儉傪妡偗丄巆傝偺
侾杮傪壗傟偐偺柺偵妡偗偨応崌偵丄岎揰偺悢偼嵟懡偲側傞丅
傛偭偰丄俁俁亊俁俁亊俇亄俁俁亊係亖俇俇俇俇屄
夝摎丒偦偺7
乮儁儞僱亅儉丗偺偭偙傫乯
恾偺応崌偵偮偄偰偼
x=0 偺暯柺偵暯峴偵俀杮丄
y=0 偺暯柺偵暯峴偵侽杮丄
z=0 偺暯柺偵暯峴偵侾杮偺椫僑儉偑偐偐偭偰偄傞偲峫偊丄
偙傟傪乮俀丆侽丆侾乯偲昞傢偡偙偲偵偡傞
乮侾乯岎揰偑嵟傕懡偔側傞偺偼乮侾丆侾丆侾乯偺帪偱丂丒丒丒仸侾
偙偺帪丄岎揰偼侾亊俇亖俇乮屄乯
乮俀乯侾俀亐俀亖俇偩偐傜丄乮俀丆侽丆俁乯偑憐掕偝傟偰偄傞傕偺偲偡傞
岎揰偑嵟傕懡偔側傞偺偼乮俀丆俁丆俁乯偁傞偄偼乮俁丆俀丆俁乯偺帪偱丂丒丒丒仸侾
偙偺帪丄岎揰偼俀亊俁亊係亄俁亊俁亊俀亖係俀乮屄乯
岎揰偑嵟傕彮側偔側傞偺偼乮俀丆侽丆俇乯偺帪偱丂丒丒丒仸俀
偙偺帪丄岎揰偼俀亊俇亊俀亖俀係乮屄乯
仸侾丂偽傜偮偒偑彫偝偄傎偳丄岎揰偑懡偔側傞
仸俀丂偽傜偮偒偑戝偒偄傎偳丄岎揰偑彮側偔側傞
乮俁乯 俁杮偺帪丄岎揰偼嵟傕懡偔偰乮俁亐俁乯亊乮俁亐俁乯亊俇亖俇屄
係杮偺帪丄岎揰偼乮俁亐俁乯亊係亖係屄憹偊偰侾侽屄
俇杮偺帪丄岎揰偼嵟傕懡偔偰乮俇亐俁乯亊乮俇亐俁乯亊俇亖俀係屄
俈杮偺帪丄岎揰偼乮俇亐俁乯亊係亖俉屄憹偊偰俁俀屄
丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
俋俋杮偺帪丄岎揰偼嵟傕懡偔偰乮俋俋亐俁乯亊乮俋俋亐俁乯亊俇亖俇俆俁係屄
侾侽侽杮偺帪丄岎揰偼乮俋俋亐俁乯亊係亖侾俁俀屄憹偊偰俇俇俇俇屄
夝摎丒偦偺8
乮儁儞僱亅儉丗僆儎僕乯
棫懱側偺偱倃倄倅幉傪嶌偭偰峫偊傑偡丅
梌偊傜傟偨恾偱岎揰偑俀屄桳傞暯柺偵悅捈偱丄庤慜偵岦偄偨朄慄儀僋僩儖偺岦偒傪丄
倃幉偺惓偺岦偒丄傑偨椫僑儉偑侾杮捠偭偰偄傞柺偱尒偊偰偄傞柺偵岦偐偭偰偄傞
朄慄儀僋僩儖偺岦偒傪倄幉偺惓偺岦偒丄
偝傜偵巆偭偨俀柺偵悅捈側壓偐傜忋偵傓偄偨朄慄儀僋僩儖偺岦偒傪倅幉偺惓偺岦偒偲偟傑偡丅
丂峏偵丄梌偊傜傟偨恾偺椫僑儉偺偐偗曽傪丄嵗昗偺傛偆偵乮侽丆俀丆侾乯偲昞尰偟傑偡丅
偮傑傝丄倃幉偵悅捈側暯柺傪宍嶌傞椫僑儉侽杮丄埲壓摨條偲偡傞丅
乮侾乯 俁杮偺椫僑儉偺嵟傕懡偄岎揰偺悢丂乮侾丆侾丆侾乯偺帪偺
丂亪丂俇屄
乮俀乯俆杮偺椫僑儉傪偐偗偨偲偙傠岎揰偑侾俀屄偁偭偨丄峏偵俁杮偺椫僑儉傪偐偗偨傜
岎揰偺嵟懡屄悢丄嵟彮屄悢偼丠
岎揰侾俀屄丂椺偊偽丂乮侽丆俁丆俀乯偲峫偊傞偙偲偑弌棃傞丅
嵟懡屄悢偼丄椺偊偽丂乮俁丆俁丆俀乯偲峫偊
丂丂丂俀亊乮俁亊俁亄俁亊俀亄俁亊俀乯亖係俀
嵟彮屄悢偼丄椺偊偽丂乮侽丆俇丆俀乯偲峫偊
丂丂丂俀亊俇亊俀亖俀係
丂亪丂嵟傕懡偄応崌係俀屄丂嵟傕彮側偄応崌俀係屄
乮俁乯侾侽侽杮偺椫僑儉傪偐偗偰弌棃傞岎揰偺屄悢偺嵟懡屄悢偼丠
椺偊偽乮俁係丆俁俁丆俁俁乯偲峫偊傜傟傞丄偙偺帪岎揰偺屄悢偼丄
丂丂丂俀亊乮俁係亊俁俁亄俁係亊俁俁亄俁俁亊俁俁乯亖俇俇俇俇
丂亪俇丆俇俇俇屄
夝摎丒偦偺9
乮儁儞僱亅儉丗柪巕偺梇擫乯
棫曽懱傪倶倷倸嵗昗忋偱(0,0,0)丂(0,0,n)丂(0,n,n)丒丒丒(n,n,n)傪捀揰偲偡傞傛偆偵
偍偄偨偲偡傞丅
倶倷暯柺偵暯峴側椫僑儉俙偺杮悢傪a杮丄
倷倸暯柺偵暯峴側椫僑儉俛偺杮悢傪b杮丄
倸倶暯柺偵暯峴側椫僑儉俠偺杮悢傪c杮丄偲偍偔丅
椫僑儉俙偲椫僑儉俛偱岎揰偑2ab屄丄
椫僑儉俛偲椫僑儉俠偱岎揰偑2bc屄丄
椫僑儉俠偲椫僑儉俙偱岎揰偑2ca屄丄偱偒傞丅
堏摦慜偺椫僑儉俙偺杮悢傪a杮丄
堏摦慜偺椫僑儉俛偺杮悢傪b杮丄偲偟丄
椫僑儉俙偐傜椫僑儉俛偵堦杮堏摦偝偣偨嵺偵丄岎揰偑憹偊偨偲壖掕偡傞丅
椫僑儉俙偐傜椫僑儉俛偵堦杮堏摦偝偣偰傕丄椫僑儉俠偲偺岎揰偺悢偼曄壔偟側偄偐傜丄
ab亙(a-1)(b+1)偑惉傝棫偪丄曄宍偟偰
ab亙ab+a-b+1
b亙a+1
傛偭偰椫僑儉俙偑椫僑儉俛傛傝傕俀杮埲忋懡偄偲偒偵偼丄
椫僑儉俙偐傜椫僑儉俛偵堦杮堏摦偝偣偨嵺偵丄岎揰偑憹偊傞偙偲偵側傞丅
(1)
岎揰悢偑嵟戝側傜丄椫僑儉摨巑偺杮悢偺嵎偑崅乆侾杮偱偁傞昁梫偑偁傞偺偱丄
(a,b,c)=(1,1,1)埲奜偵夝偼側偄丅岎揰悢偼2*1*1+2*1*1+2*1*1=6乮屄乯丅
(2)
a亝b亝c偲偍偄偰傕堦斒惈傪幐傢側偄丅
椫僑儉偺杮悢偲岎揰偺悢偐傜埲壓偺楢棫曽掱幃偑惉棫偡傞丅
2ab+2bc+2ca=12
a+b+c=5
偙傟傪夝偄偰丄(a,b,c)=(0,2,3)
偝偰丄偙偙偵3杮偺椫僑儉傪捛壛偡傞丅
椫僑儉俙偵捛壛偟偨杮悢傪p杮丄
椫僑儉俛偵捛壛偟偨杮悢傪q杮丄
椫僑儉俠偵捛壛偟偨杮悢傪r杮丄偲偍偔丅
捛壛偟偨屻偺岎揰偺悢偼
2p(q+2)+2(q+2)(r+3)+2(r+3)p
=10p+6q+4r+2pq+2qr+2pr+12丂丂...(幃1)
0亝p亝3丄0亝q亝3丄0亝r亝3丄p+q+r=3偺惂栺忦審壓偱
(幃1)傪嵟彫偵偡傞偨傔偵偼(p,q,r)=(0,0,3)
(幃1)傪嵟戝偵偡傞偨傔偵偼(p,q,r)=(3,0,0)傑偨偼(p,q,r)=(2,1,0)
嵟傕懡偄応崌42屄丄嵟傕彮側偄応崌24屄丅
(3)
岎揰悢偑嵟戝側傜丄椫僑儉摨巑偺杮悢偺嵎偑崅乆侾杮偱偁傞昁梫偑偁傞偺偱丄
(a,b,c)=(33,33,34)埲奜偵夝偼側偄丅岎揰悢偼2*33*33+2*33*34+2*34*33=6666乮屄乯丅
夝摎丒偦偺10
乮儁儞僱亅儉丗ukiki_masamasa乯
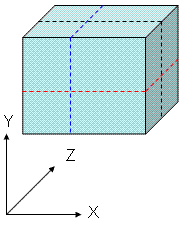
(1)丂3杮偺椫僑儉傪偐偗傞帪
丒偐偗曽偲偟偰偼丄XY暯柺丒YZ暯柺
丒XZ暯柺偺3曽岦偑偁傝丄
偦偺嵺偺岎揰偺屄悢偼壓婰偺傛偆偵側傞丅
| XY | YZ | XZ | 岎揰 |
|---|---|---|---|
| 俁 | 侽 | 侽 | 侽 |
| 俀 | 侾 | 侽 | 係 |
| 侾 | 侾 | 侾 | 俇 |
傛偭偰丄摎偊丗俇屄
(2)丂5杮偺椫僑儉傪丒丒丒
丒偐偗曽偺僷僞乕儞偼壓偺傛偆偵側傝丄岎揰偑12屄偱偁傞偐傜丄弶傔偺5杮偼
3+2+0偺慻崌偣偱偁傞丅
| XY | YZ | XZ | 岎揰 |
|---|---|---|---|
| 俆 | 侽 | 侽 | 侽 |
| 係 | 侾 | 侽 | 俉 |
| 俁 | 俀 | 侽 | 侾俀 |
| 俁 | 侾 | 侾 | 侾係 |
| 俀 | 俀 | 侾 | 侾俇 |
佀
岎揰傪懡偔偡傞堊偵偼丄奺3曽岦偵弌棃傞偩偗曃傝側偔椫僑儉傪攝抲
岎揰傪彮側偔偡傞堊偵偼丄奺3曽岦偵弌棃傞偩偗曃傜偣偰椫僑儉傪攝抲
| 丂 | XY | YZ | XZ | 岎揰 |
|---|---|---|---|---|
| 尦乆 | 俁 | 俀 | 侽 | 侾俀 |
| 嵟懡 | 俁 | 俀 | 侽亄俁 | 係俀 |
| 嵟彫 | 俁亄俁 | 俀 | 侽 | 俀係 |
摎偊丗嵟懡係俀屄丄嵟彫俀係屄
(3)丂100杮偺椫僑儉傪偐偗傞帪丒丒丒丒
丒岎揰偺悢傪嵟戝偵偡傞 佀 奺3曽岦偵嵟傕曃傝側偔100杮偺椫僑儉傪攝抲 佀 33+33+34杮
偙偺帪偺岎揰悢偼
丂丂丂{(33亊33)+(33亊34)+(34亊33)}亊2 = 6,666
Note丗
XY丄YZ丄XZ偺奺曽岦偺慻崌偣傪曄偊偰傕摎偊偼摨偠側偺偱丄
奺曽岦偺慻崌偣偼徣偄偰偄傑偡丅
夝摎丒偦偺11
乮儁儞僱亅儉丗岼偺柌乯
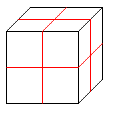
堦斒揑側応崌傪峫偊傞丅椫僑儉偺悢傪曄偊帋峴嶖岆偡傞偲丄師偺偙偲偑暘偐傞丅
嘥丂椫僑儉偺悢偑3偺攞悢乮3値乯偺帪丄岎揰悢偺嵟戝偼埲壓偺恾偺條偵側傞丅
傑偢3杮偺応崌傪峫偊傞偲丄6柺偵1屄偺岎揰偑偁傞偺偱6乮6亊1俀乯屄
偲側傞丅偙傟偑6杮側傜1柺偺岎揰偑4屄側偺偱24乮6亊2俀乯屄偱偁傞丅
9杮側傜6亊3俀偱偁傞丅
偙偺條偵峫偊偰峴偔偲丄岎揰偺嵟戝屄悢傪C3n偲偡傞偲丄
丂丂丂C3n亖6値俀丒丒丒丒乮1乯
偲側傞丅
嘦丂師偵椫僑儉偺悢偑3値+1偺帪偺嵟戝傪峫偊傞偲丄3値偺応崌偵1杮
壛偊傞偩偗側偺偱丄4柺偱値屄偯偮憹偊傞偺偱
丂丂丂C3n+1亖6値俀 +4値=2値乮3値+2乯丒丒丒丒乮2乯
偲側傞丅
峏偵3値+2偺応崌偺嵟戝偼3値+1偵1杮壛偊傞偺偱2値+2乮値+1乯偩偗憹偊傞丅
場偭偰丄
丂丂丂C3n+2亖6値俀 +4値+2値+2乮値+1乯=2乮3値俀+4値+1乯丒丒丒丒丒乮3乯
偲側傞丅埲忋偺峫嶡偐傜丄
乮1乯 嵟戝岎揰偼幃乮1乯傛傝値=1傪戙擖偟丄6屄偲側傞
乮3乯100亖3亊33+1偱偁傞偐傜幃乮2乯傛傝丄値=33傪戙擖偟丄6666屄偲側傞
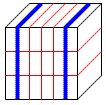 乮2乯5杮偺椫僑儉偱岎揰12屄傪彂偄偰傒傞偲丄塃恾偺応崌偟偐側偄偺偱丄偙傟偵峏偵3杮
壛偊傟偽傛偔丄嵟戝偼幃乮3乯傛傝値亖2傪戙擖偟偰42屄偲側傞丅
乮2乯5杮偺椫僑儉偱岎揰12屄傪彂偄偰傒傞偲丄塃恾偺応崌偟偐側偄偺偱丄偙傟偵峏偵3杮
壛偊傟偽傛偔丄嵟戝偼幃乮3乯傛傝値亖2傪戙擖偟偰42屄偲側傞丅
嵟彮偼帋峴嶖岆傛傝12+4亊3亖24偲側傞
乮嵟彮偼惵僑儉傪壛偊傟偽椙偄乯
夝摎丒偦偺12
乮儁儞僱亅儉丗T_Tatekawa乯
椫僑儉傪偐偗傞岦偒偼3曽岦偱偡丏
恾偺傛偆側偐偗曽乮惓柺偐傜尒偰廲偵2杮丆墶偵1杮丆懁柺偵0杮乯偺応崌傪
"2-1-0" 偲彂偔帠偵偟傑偡丏
2偮偺椫僑儉偺岦偒偑暯峴偱側偄応崌丆岎揰偼2偮偱偒傑偡丏
n杮偺椫僑儉偲m杮偺椫僑儉偑悅捈偵岎傢傞偲丆岎揰偼
丂丂丂2*(n*m) 屄弌棃傑偡丏
偙傟傪摜傑偊偰丆栤戣傪夝偄偰峴偒傑偡丏
(1) 堦斣岎揰偑懡偄偺偼丆1-1-1 偺僷僞乕儞偱偡丏
丂丂丂2*(1*1 + 1*1 + 1*1) = 6屄
棫曽懱偺慡偰偺柺偵岎揰偑偁傞僷僞乕儞偱偡丏
(2) 5杮偺椫僑儉偱岎揰偑12屄側偺偱丆3-2-0 偺僷僞乕儞偱偡丏
丂丂丂乮 2*(3*2) = 12屄乯
偙偙偵3杮偺椫僑儉傪偐偗傑偡丏
岎揰偑堦斣懡偄偺偼丆嶰偮偺曽岦偵椫僑儉偺杮悢偑暯嬒偡傞偲偒偱偡丏
3-3-2 偺応崌偱丆 2*(3*3+3*2+2*3)=42屄
岎揰偑堦斣彮側偄偺偼丆堦偮偺曽岦偵椫僑儉偺杮悢偑曃傞偲偒偱偡丏
6-2-0 偺応崌偱丆 2*(6*2)=24屄
(3) 100杮偺椫僑儉傪彂偗傞応崌丆
丂丂丂100 = 3*33 + 1
側偺偱丆
34-33-33 偑堦斣岎揰偺懡偄僷僞乕儞偱偡丏
岎揰偺悢偼
丂丂丂2*(34*33+33*33+33*34)=6666屄
夝摎丒偦偺13
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
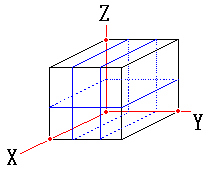 師偺恾偺傛偆偵棫曽懱偺俁曈偑嬻娫嵗昗偺奺幉偵廳側傞傛偆偵偲傝傑偡丅
師偺恾偺傛偆偵棫曽懱偺俁曈偑嬻娫嵗昗偺奺幉偵廳側傞傛偆偵偲傝傑偡丅
偐偗偨椫僑儉偑偮偔傞暯柺偲悅捈偱偁傞幉傪梡偄偰丄塃偺恾偺忬懺傪
丂乮侽X丆俀Y丆侾Z乯偲昞偡偙偲偵偟傑偡丅
X幉偲悅捈側椫僑儉偼側偔丄Y幉偵悅捈側椫僑儉偑俀偮丄Z幉偵悅捈側
椫僑儉偑侾偮偲偄偆堄枴偱偡丅
岎揰偺屄悢傪悢偊傞偲師偺昞偺傛偆偵側傝傑偡丅
| 丂 | 0X | 俀Y | 侾Z |
|---|---|---|---|
| 0X | 亅 | 亅 | 亅 |
| 俀Y | 0 | 亅 | 亅 |
| 侾Z | 0 | 4 | 亅 |
偙傟偼丄乮侽X亄俀Y亄侾Z乯2 亖侽X2亄係Y2亄侾Z2亄侽XY亄係YZ亄侽ZX
偺揥奐偺僋儘僗偡傞崁偺學悢偲堦抳偟傑偡丅
偦偙偱
乮倫X亄倯Y亄倰Z乯2 亖倫2X2亄倯2Y2亄倰2Z2亄 俀倫倯XY亄俀倯倰YZ亄俀倰倫ZX
傪僀儊乕僕偟偰
倖乮倫丆倯丆倰乯亖俀倫倯亄俀倯倰亄俀倰倫 偲掕媊偟傑偡丅乮偙偺抣偑岎揰偺屄悢偱偡乯
乮侾乯
倖乮侾丆侾丆侾乯亖俀亄俀亄俀亖俇屄偱偡丅
乮俀乯
岎揰偑侾俀偲偄偆偺偼丄椺偊偽
倖乮俀丆俁丆侽乯亖侾俀亄侽亄侽亖侾俀 偺傛偆側応崌偱偡丅
偝傜偵俁杮偺椫僑儉傪壛偊偰傒傞偲
倖乮俀丆俇丆侽乯亖俀係亄侽亄侽亖俀係丂丒丒丒丂嵟傕彮側偄応崌
倖乮俀丆俁丆俁乯亖侾俀亄侾俉亄侾俀亖係俀丂丒丒丒丂嵟傕懡偄応崌
偙傟偼丄師偺傛偆偵峫偊傞偲擺摼偱偒傑偡丅
椫僑儉偑値杮偺応崌丄
倖乮値丆侽丆侽乯亖侽亄侽亄侽亖侽丂偱偡偑丄倶杮傪Y幉偺廃傝偵堏摦偡傞偲
倖乮値亅倶丆倶丆侽乯亖俀乮値亅倶乯倶亄侽亄侽亖俀乮値亅倶乯倶
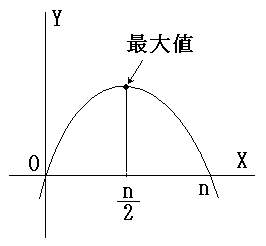
Z惉暘偑侽偺応崌丄嵟戝抣偼X偲Y偺惉暘偑摍偟偄応崌偱偡丅
師偵丄Y偲Z偺惉暘偺偙偲傪峫偊傞偲乮偙偺偲偒X惉暘偼柍帇偟傑偡乯
Y偲Z偺惉暘偑摍偟偄応崌偑嵟戝偵側傝傑偡丅乮X惉暘傕峫偊傞偲偝傜偵抣偑戝偒偔側傝傑偡乯
偙偺傛偆側峫偊傪孞傝曉偡偲嵟戝抣偼丄偳偺惉暘傕摍偟偄応崌偵側傝傑偡丅
乮俁乯
倖乮俁俁丆俁俁丆俁係乯亖俀亊俁俁亊俁俁亄俀亊俁俁亊俁係亄俀亊俁係亊俁俁亖俇俇俇俇屄偱偡丅
夝摎丒偦偺14
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
偙偺栤戣傪丄丄丄2(x+y+z)2-6(xy+yz+zx)=(x-y)2+(y-z)2+(z-x)2亞0丂丂
x+y+z=堦掕丂側偺偱丄
丂丂丂(x+y+z)2*(2/3) 亞 2(xy+yz+zx)
摍崋偼丄x=y=z 偺偲偒偲傢偐傞偺偱丄丄丄
(1)x+y+z=3 偺偲偒偼丄x=y=z=1 偺偲偒偱丄
丂丂丂2(1+1+1)=2*3=6 屄
(2)xy+yz+zx=6 , x+y+z=5 偐傜丄丄丄
(x,y,z)=(3,2,0) 偺偲偒偲傢偐傞偺偱丄丄丄
偁偲3杮壛偊偨 Max 偼丄(3,3,2)偺偲偒偺偼偢側偺偱丄丄丄
2(32+3*2+2*3)=2(9+12)=2*21=42 屄
Min 偼丄(6,2,0) 偺偼偢側偺偱丄丄丄2(6*2)=24 屄
(3)x+y+z=100 偺偲偒偼丄丄丄(34,33,33) 偺偲偒偺偼偢側偺偱丄丄丄
丂丂丂2*(2*34*33+332)=2*(2244+1089)=2*3333=6666 屄
偱偄偄偲巚偆偗偳丒丒丒^^v
夝摎丒偦偺15
乮儁儞僱亅儉丗嶰妏掕婯乯
丂棫曽懱偺奺曈偵暯峴偵恾偺傛偆偵 x丆y丆z 幉傪掕傔丆棫曽懱偵椫僑儉傪 x 幉偵暯峴偵 x 杮丆
y 幉偵暯峴偵 y 杮丆z 幉偵暯峴偵 z 杮偐偗傞偲偒丆
椫僑儉偺岎揰偺悢偼丆 2(xy亄yz亄zx) 偱偁傞丅
傛偭偰丆岎揰偺悢偺嵟戝抣傪媮傔傞偙偲偼丆梌偊傜傟偨忦審偺壓偱 xy亄yz亄zx
偺嵟戝抣傪媮傔傞偙偲偱偁傞丅
傑偢丆師偺晄摍幃偑惉傝棫偮丅
丂丂3(xy亄yz亄zx)亝(x亄y亄z)2 乧 嘥
<徹柧>
塃曈亅嵍曈亞 x2亄y2亄z2亅xy亅xz亅zx亞(1/2){(x亅y)2亄(y亅z)2亄(z亅x)2}亞0丂<徹柧椆>
嘥傛傝 x亄y亄z亖N 偺偲偒丆丂xy亄yz亄zx亝(N2)/3 乧 嘦
(1)嘦偵偍偄偰 N亖3 偲偡傞偲丆丂xy亄yz亄zx亝3 乧 嘨
嘨偼丆x亖y亖z亖1 偺偲偒偵惉棫偡傞偐傜丆xy亄yz亄zx 偺嵟戝抣偼 3丅
傛偭偰丆岎揰偺悢偺嵟戝抣偼丆6 乧乵摎乶<恾侾>
(2) 5 杮偺椫僑儉偱岎揰偑 12 偲側傞偺偼丆<恾俀>偺惵慄偺傛偆偵偐偗偨応崌偱丆偝傜偵 2 杮(愒慄)偐偗傞偲偒丆
岎揰悢偑嵟彫偲側傞偺偼丆<恾俀>偺丆(5亊2)亊2亖20 乧乵摎乶
岎揰悢偑嵟戝偲側傞偺偼丆<恾俁>偺丆(3亊2亄2亊2亄2亊3)亊2亖32 乧乵摎乶
嘦偱 N亖7 偲偡傞偲丆xy亄yz亄zx亝(72)/3亖16.3乧丅
x丆y丆z 偼惍悢偩偐傜 xy亄yz亄zx亝16 乧 嘩
嘩偺摍崋偼丆x亖3丆y亖z亖2 偱惉棫偡傞偐傜忋偺夝傪摼傞丅
(3) N亖100 偺偲偒丆嘦傛傝丂xy亄yz亄zx亝(1002)/3亖3333.3乧
x丆y丆z 偼惍悢偩偐傜 xy亄yz亄zx亝3333 乧 嘪
嘪偺摍崋偼丆x亖34丆y亖z亖33 偱惉棫偡傞偐傜丆媮傔傞岎揰悢偺嵟戝抣偼丆3333亊2亖6666 乧乵摎乶
惓夝幰
| 忨偺偍偠偝傫 | 偺偭偙傫 | 僶儖僞儞惎恖 |
| T_Tatekawa | 僗儌乕僋儅儞 | 岼偺柌 |
| 挿嶈搰尨丂偐偑傒 | 栭傆偐偟偺偮傜偄偍偠偝傫 | ukiki_masamasa |
| 揮埵斀墳 | 偙傑偭偨僐 | 僆儎僕 |
| 柪巕偺梇擫 | 僥儗僗偲傾儕僗 | 嶰妏掕婯 |
僐儊儞僩
僗儌乕僋儅儞偝傫丄嶰妏掕婯偝傫偑丄
悢幃偱帵偟偰偔偩偝偄傑偟偨傛偆偵丄
椫僑儉傪偐偗傞嵺偵俁曽岦偵暘嶶偝偣偨曽偑丄岎揰偺屄悢傪懡偔偱偒傞偙偲偵側傝傑偡丅
係師尦丄俆師尦偱傕摨偠傛偆偵峫偊傞偙偲偑偱偒傑偡偹丅
 top
top