136.ジュースの問題
あるジュースは1本 120 円で、1本に1枚のシールがついています。
このシールを8枚集めると、ジュースを1本もらうことができます。
シールを集めてもらったジュースにもシールがついています。
次の問に答えなさい。
(1) 6,000円で得ることができるジュースは、最大何本ですか。
(2) 300本のジュースが必要なとき、最低いくらかかりますか。
問題の出典
センスのよい脳をつくる 大人の算数パズル
河瀬 厚 著
自由国民社
立教新座中学校 2006年
答えと解説
解答・その1
(ペンネ−ム:やなせ)
問い1について
6000÷120=50本
50枚÷8枚=6本・・・2枚
(6+2)÷8=1
問い1答え 50+6+1=57本です。
問い2について
960円で9本だから
300本÷9本=33.33333
9本×33=297本
残り3本だから
960×33+360=32040です・・これが最初の思いつきですが
これでは最初に267本買えます。
267(おまけシール枚数)÷8=33本・・・3
(33+3)÷8=4本・・・4
(4+4)÷8=1本
267+33+4+1=305本になる
そこで5本分600円を資金から減らし31440円で再スタート
31440÷120=262本(おまけシールも262枚)
262÷8=32・・・・・6
(32+6)÷8=4・・・・6
(4+6)÷8=1・・・・2
262+32+4+1=299本
これでは足らないので31440円に1本分120円を足した
31440+120=31560で再々計算
31560÷120=263
263÷8=32・・・・7
(32+7)÷8=4・・・・7
(7+4)÷8=1・・・・・3
263+32+4+1=300
ばんざ〜〜いやっと出来ました。
問い2答え 31560円必要
解答・その2
(ペンネ−ム:T_Tatekawa)
(1) まず 6000円では
6000 / 12 = 50
で50本買えます.シールが50枚あるので,
50 = 6*8 + 2
で 6 本もらえます.この 6本についているシールと,
残ったシール2枚でさらにもう1本もらえます.
合計で 50+6+1 = 57 本.
(2) 8本分のお金,つまり 120*8=960円で 9本得る事が出来ます.
数を増やしていくと,1度目に買ったジュースのシールを使って
2度目にジュースがもらえます.
ジュースの本数を増やしていくと,
8-14本買うとおまけが1本
15-21本買うとおまけが2本
22-28本買うとおまけが3本
...
という様に,7本ごとにおまけの本数が増えていく事が分かります.
さらに,n本のおまけをもらうには,
7n+1 本以上 7(n+1) 本以下買えばいいのです.
さて,この式に従うと,合計のジュースの本数について
8n+1 ≦ 300 ≦ 8(n+1)
を満たす整数 n を見つければいい事になります.
292 ≦ 8n
8n ≦ 299
から,n=37 です.
300-8*37 = 4
なので,お金を出して買う本数は
120*(7*37+4) = 120 * 263 = 31560円
以下,検算:
1) 263本買うと,シールが263枚.
2) シール256枚を使って32本もらう.残りのシールは39枚.
3) シール32枚を使って4本もらう.残りのシールは11枚.
4) シール8枚を使って1本もらう.シールが4枚余る.
263+32+4+1=300
解答・その3
(ペンネ−ム:テレスとアリス)
(1) 6000円で、まず50本のジュースを買うことができます。
6000÷120=50
次に、50枚のシールで6本のジュースをもらうことができます。
50÷8=6
さらに、残りのシール2枚と、6枚のシールで1本のジュースをもらうことができます。
50+6+1=57
よって、57本のジュースを得ることができます。
(2) 64本のジュースを買い、そのシールで8本のジュースをもらい、さらにもう1本もらいます。
これをあと3回、全部で4回行います。
この時点で、ジュースは292本です。
買ったジュースは、64×4=256
貰ったジュースは、 9×4=36
シールは4枚残っています。
あと8本必要なので、まず4本買って、シール8枚で1本もらい、
最後に3本買って、合計300本になります。
買ったジュースは、256+4+3=263
貰ったジュースは、36+1=37
使った金額は、263×120=31560円になります。
解答・その4
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
答え
答え (1) 57本 (2) 31560円
(1) 6000/120=50本
50枚/8枚=6本あまり2枚
6枚+2枚=8枚→1本
合計 50+6+1=57本
(2)この問題を考える時に次の方法で答えに到達いたしました。
シールで交換出来ますので300本は購入する必要はありません。
1回目の試算、250本を購入したとして計算します。
250÷8=31と余り2 31÷8=3と余り5 シール2+5=7枚余り
手に入れたジュースは250+31+3=284本なので300本に16本足りない。
2回目の試算、260本を購入したとして計算します。
260÷8=32と余り4 32÷8=4余り0 シール4+0=4枚余り
手に入れたジュースは260+32=292本なので300本に8本足りない。
3回目の試算、264本を購入したとして計算します。
264÷8=33と余り0 33÷8=4余り1 シール0+1=1枚余り
手に入れたジュースは264+33+4=301本なので300本に1本多い。
4回目の試算、263本を購入したとして計算します。
263÷8=32と余り1 32÷8=4余り0 シール1+0=1枚余り
手に入れたジュースは263+32+4=300本なので263本購入したと決定した。
従って購入代金は263×120円=31560円です。
解答・その5
(ペンネ−ム:のっこん)
(1)6000÷120=50
50本買うと何本を得るかという問題になる
A.まず1本買う・・・シール数1
B.7本買って(シール数8)、1本もらう・・・シール数1
以下Bを繰り返す
Bを7回繰り返すと、49本買って7本もらうことになる
最初に1本買っているから、50本買うと57本を得ることになる
(2) 同様にして
A.まず1本買う
B.7本買って1本もらう
以下Bを繰り返す
ここでBを「7本が8本に化ける」と考える
299÷8=37.375 だから
Bを37回繰り返すと
7×37=259(本)が、8×37=296(本)に化けることになる
299本にするためには3本を買い足さなければならないから
結局、300本を得るには
1+259+3=263(本)買わなければならない
120×263=31560(円)
解答・その6
(ペンネ−ム:こまったコ)
(1)
ジュースは1本120円なので、6000円で買えるジュースは50本。手に入るシールは50枚。
シール8枚ごとにもう1本もらえるので50枚では 50÷8=6 6本もらえる。
ジュースに換えていないシールの残り2枚と新しくもらったジュースのシール6枚の合計8枚で
もう1本もらえる。
50+6+1=57 最大57本もらえる。
(2)
ジュース8x8=64本で8本もらえるのでそれでもう1本(aとする)もらえる。
ここまでで64+8+1=73本。手元にあるシールはaの1本の1枚。
ここまでで買ったジュースは64本。
さらに8x7=56本のシールででもらえる7本のシールと
先ほどのaの1本のシールででもう1本(bとする)もらえる。
ここまでで73+56+7+1=137本。手元にあるシールは1枚。
ここまでに買ったジュースは64+56=120本。
さらに8x7=56本のシールででもらえる7本のシールと
先ほどのbの1本のシールででもう1本(cとする)もらえる。
ここまでで137+56+7+1=201本。手元にあるシールは1枚。
ここまでに買ったジュースは120+56=176本。
さらに8x7=56本のシールででもらえる7本のシールと
先ほどのcの1本のシールででもう1本(dとする)もらえる。
ここまでで201+56+7+1=265本。手元にあるシールは1枚。
ここまでに買ったジュースは176+56=232本。
後35本欲しい。8x3=24本で3本もらえる。ここまでで265+24+3=292本。
後7本と先ほどのdの1本のシールでもう1本もらう。
これで292+7+1=300本。
ここまでに買ったジュースは232+24+7=263本。
120x263=31560円必要。
解答・その7
(ペンネ−ム:長崎島原 かがみ)
(1)
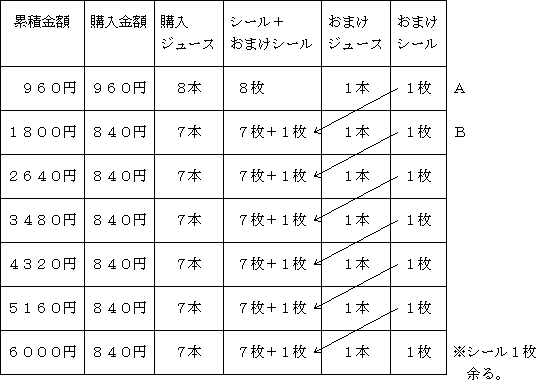
したがって、全部で57本得ることができる。
(2)
|
ジュースの本数 A+B×36=9+8×36=297本+シール1枚余り 購入金額 960+840×36=31,200円 |
あと3本買うと300本になる。シールは4枚になるが、ジュースは得られない。
ジュース3本=360円
したがって、31,200+360=31,560円
解答・その8
(ペンネ−ム:巷の夢)
(1) 題意に沿って書き出してみると以下の表のようにまとめられる。
| ジュース単価 (円) | 買った本数 (本) | おまけの本数 (本) | 飲んだ本数 (本) | 支払った金額 (円) |
|---|---|---|---|---|
| 120 | 8 | 8 | 960 | |
| 120 | 7 | 1 | 8 | 840 |
| 120 | 7 | 1 | 8 | 840 |
| 120 | 7 | 1 | 8 | 840 |
| 120 | 7 | 1 | 8 | 840 |
| 120 | 7 | 1 | 8 | 840 |
| 120 | 7 | 1 | 8 | 840 |
| 120 | 1 | 1 | 0 | |
| 合計 | 57 | 6000 |
即ち、6000=960+840*M+120*Nとなる。 この方程式でMの値は上表の様に6、N=0となる場合に6000円となる。 因って飲んだ本数は8*7+1=57本が最大である。
(2) 上記(1)より300=8*X+Yとなる。
即ち、X=37、Y=4ところが最後の8本を飲むとおまけ
に1本もらえるので、実質的にはY=3である。
因って、支払った金額は、
960+840*36+120×3=31560円
が最低コストである。
解答・その9
(ペンネ−ム:スモークマン)
(1)
6000/120=50
50/8=6・・・2
6/8=1・・・2
結局、、、50+6+1=57 本飲めちゃう♪
(2)
8本買えば1本おまけがつくので、、、
300/9=33・・・3
33/9=3・・・6
(3+6)/9=1
つまり、33*8-1=263 本ですね。
実際に、263/8=32・・・7
32/8=4
(7+4)/8=1
263+32+4+1=300 ♪
263*120=31560 円で飲めますね ^^v
解答・その10
(ペンネ−ム:転位反応)
(1) 6,000円で50本のジュースを購入して、シール50枚を獲得できる
シール50枚で6本のジュースと交換し、2枚のシールが余る。
6本のジュースで獲得したシールと合わせると8枚になり、
さらに、ジュース1本と交換できる
従って、6,000円で得られるジュースは、最大で50+6+1=57本
(2) 8本分の代金で9本のジュースを獲得できるので、
300=33×9+3
33本のジュースは、代金を支払わずにシールとの交換で獲得できる
さらに、その分の33枚のシールで4本のジュースを獲得できる
従って、代金を払って購入するジュースは、300‐33‐4=263本
代金は、120×263=31,560円
解答・その11
(ペンネ−ム:夜ふかしのつらいおじさん)
(1)
6000÷120=50 より 50本 のジュースが買えます。
だから50枚のシールが手元にあります。

このシールをジュースに替えると 6本 になります。
だから残りのシールと合わせて8枚のシールがあります。

このシールをジュースに替えると 1本 になります。
シールが1枚残ります。
ジュースは合計 57本 になります。
(2)
シール8枚で1本のジュースと交換すると、シールが1枚ついてきます。
だからシールとジュースと交換すると、7枚シールが減ることになります。
x本のジュースを買ったとすると、x枚のシールがあることになります。
だから、
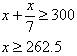
より、263本×120=31560円必要です。
解答・その12
(ペンネ−ム:バルタン星人)
(1)57本
(2)31560円
買うジュースを○、おまけを★で表すと
○、(○○○○○○○★)以降、()の繰り返しとなる。
最初の1本は120円、次の8本は840円なので
(6000−120)÷840=7
変える本数は1+8×7=57
(300−1)÷8=37余り3
840×37+120×4=120×263=31560
この手の問題、中学入試に出てきます。子供の家庭教師用に
算数を勉強したとき、この考え方を知りました。
(1)の別解、とりあえず50本買い、50枚のシールで交換していくと
6000÷120=50
50÷8=6余り2
(6+2)÷8=1
50+6+1=57
解答・その13
(ペンネ−ム:ukiki_masamasaの子供)
(1)6,000円では
A 6,000円で買える本数は、6000/120=50本 → シール 50枚
B シール50枚は、50/8=6…2だから、おまけ6本とシール2枚になる
C おまけ6本から6枚のシールが出てくるから、先ほどの余ったシールと合わせて6+2=8でまた「おまけ1本」
A+B+C=50+6+1=57本 答え57本
(2)300本では
○:買ったジュース
●:おまけのジュース として
1 2 3 4 5 6 7 8 1:○ ○ ○ ○ ○ ○ ○ ○ 2:● ○ ○ ○ ○ ○ ○ ○ 3:● ○ ○ ○ ○ ○ ○ ○ : : 37:● ○ ○ ○ ○ ○ ○ ○ 38:● ○ ○ ○ ⇒合計300本上の図は、300/8=37…4を表しており、○の数×120円が答えとなるから、
(37×7+1+3)×120 = 263×120 = 31,560円
もしくは、300本のうち、おまけ(●)は37本であるから、
(300-37)×120=263×120=31,560円
答え31,560円
解答・その14
(ペンネ−ム:ukiki_masamasa)
初めはシールがないので、8本買って1本おまけ=合計9本のジュースが手に入り、
1枚のシールが残る。
120×8=960円:9本
2回目以降は、前回の残りのシールが1枚あるので7本買って1本おまけ=
合計8本のジュースが手に入り、1枚のシールがまた次に残る。
120×7=840円:8本
(1)6,000円では・・・
(6,000-960)/840=6
よって、9+8×6=57本 Ans. 57本
(2)300本では・・・
(300-9)/8=36...3
よって、960+(840×36)+(120×3)=31,560円 Ans.31,560円
解答・その15
(ペンネ−ム:三角定規)
問1
1゜ 6000÷120=50 ← ジュース 50 本,シール 50 枚。 … (1)
2゜ シール 8 枚で 1 本もらえるから,
50÷8=6 あまり 2 ← ジュース 6 本,シール 8 (=6+2) 枚 …(2)
3゜ 8÷8=1 あまり 0 ← ジュース 1 本,シール 1 (=1+0) 枚 …(3)
(1)(2)(3)より,もらえるジュースは,50+6+1=57 本 …[答]
問2
シールが m 枚あるとき [m/8] 本のジュースがもらえ,シールは,
[m/8]+m−8[m/8]=m−7[m/8] …(4)
(商) (あまり)
枚となる。そして,(4)が 8 以上のとき再度この操作を繰り返すことができる。
この(商)と(あまり)は m の増加関数だから,その和(4)も m の増加関数である。
よって,題意を満たす m がひとつ見つかれば,それが解となる。
1゜ ジュースを 263 本買うと m=263。…(5)
2゜ 263÷8=32 あまり 7 ← ジュース 32 本,シール 39 (=32+7) 枚 …(6)
3゜ 39÷8=4 あまり 7 ← ジュース 4 本,シール 11 (=4+7) 枚 …(7)
4゜ 11÷8=1 あまり 3 ← ジュース 1 本,シール 4 (=1+3) 枚 …(8) ←終了
(5)(6)(7)(8)より,263+32+4+1=300 で,題意を満たす。
最初にジュースを 263 本買うためには,263×120=31,560 円 必要。…[答]
解答・その16
(ペンネ−ム:オヤジ)
[ ]:Gauss記号とするとき
nを自然数として、金額120×n(円)で購入出来るジュースの本数 m(本)は、
m=n+[n/8]+[[n/8]/8]+[[[n/8]/8]/8]+・・・+S(n)となる
ただし S(n):シールよる本数
(1) 6000=120×n を解くと n = 50
m= 50+[50/8]+[6/8]+S(50)= 50+6+0+1 ∴ 57本
※ S(50)= シール8枚分による本数=1
(2) 300本のジュースを、得られる最低金額
求める金額を120×n(円)とすると
300≦n+「n/8」+[[n/8]/8]+[[[n/8]/8]/8]+・・・+S(n)
この式を満たす最小の自然数nは、 n=263
実際 上式の右辺、263+32+4+S(263)=299+1=300
∵ S(263)=シール(263−32×8+4)枚分の本数=シール11枚分=1本
よって、求める金額は、120×263=31,560 ∴ 31,560(円)
解答・その17
(ペンネ−ム:teki)
1 57本
2 263本 ( 31,560円 )
1は実際にやってみたほうが早いです。
6000円でジュースを50本買い、シールを50枚集めます。
このうち48枚のシールをジュース6本と交換し、6枚のシールとあまった2枚
のシールでもう1本ジュースをもらえます。
2ですが、一般にN本のジュースを得るのに必要な購入本数nは以下の式で
表せます。
n=[N*8/7]+1 (ただし[ ]はガウス記号)
なぜ、このような式になるのかというと、仮に最初に1枚シールを持っていたと
すると、後は7本ずつ買い足すことによって、8本ずつのジュースを得ることが
できるからです。
最初は8本買う必要があるので、上記の式が成立します。
正解者
| こまったコ | teki | バルタン星人 |
| オヤジ | 巷の夢 | スモークマン |
| 長崎島原 かがみ | のっこん | 夜ふかしのつらいおじさん |
| 転位反応 | 杖のおじさん | やなせ |
| T_Tatekawa | ukiki_masamasa | ukiki_masamasaの子供 |
| 三角定規 | テレスとアリス |
まとめ
(1)私は、このように考えてみました。
| 回数 | ジュースの本数 | シールの枚数 |
|---|---|---|
| 1 | 50 | 50 |
| 2 | 6 | 2+6=8 |
| 3 | 1 | 0+1=1 |
| 合計 | 57 | 1 |
(2)最初に買うことのできるジュースの本数をa、シールを交換して最大入手できるジュースの本数をAとすると、
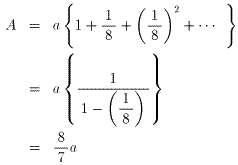
よって、
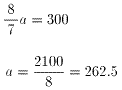
切り上げて、a=263、実際、検証してみると、
| 回数 | ジュースの本数 | シールの枚数 |
|---|---|---|
| 1 | 263 | 263 |
| 2 | 32 | 7+32=39 |
| 3 | 4 | 7+4=11 |
| 4 | 1 | 3+1=4 |
| 合計 | 300 | 4 |
であり、かつ
| 回数 | ジュースの本数 | シールの枚数 |
|---|---|---|
| 1 | 262 | 262 |
| 2 | 32 | 6+32=38 |
| 3 | 4 | 6+4=10 |
| 4 | 1 | 2+1=3 |
| 合計 | 299 | 3 |
なので、a=263である。つまり、31,560円
 top
top