135.タイルの問題・その2
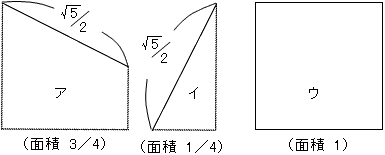
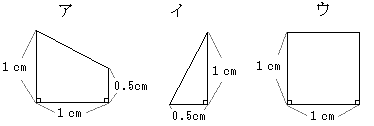 右の図のようなア~ウの3種類のタイルが、それぞれアは4枚、イは4枚、
ウは1枚あります。これらのタイルを使ってすき間なくならべ、面積が一番大きな正方形と
二番目に大きな正方形をそれぞれ作ってください。ただし、使わないタイルがあってもよいものとします。
右の図のようなア~ウの3種類のタイルが、それぞれアは4枚、イは4枚、
ウは1枚あります。これらのタイルを使ってすき間なくならべ、面積が一番大きな正方形と
二番目に大きな正方形をそれぞれ作ってください。ただし、使わないタイルがあってもよいものとします。
問題の出典
センスのよい脳をつくる 大人の算数パズル
河瀬 厚 著
自由国民社
恵泉女学園中学校 2005年
答えと解説
解答・その1
(ペンネ-ム:スモークマン)
・最大の図は、、、すべてを使ってできる図で、まん中に正方形を置いて回りに残り
をくっつければいいですね。面積は、正方形5個分=5 cm2
・2番目の面積のものは、、、4個4個を組み合わせてできる図形。=1個の正方形+3
個3個を組み合わせてできる図形=4 cm2
後者に残りのどれか1個をくっつけても正方形にできないはず、、、対称性から。。
。ちょっと直感的な話しですが、、、^^;
解答・その2
(ペンネ-ム:オヤジ)
(1)1番大きな正方形は、アとイをくっつけた3辺が、それぞれ
1cm,2cm, cmの直角三角形×4と一辺1cmの正方形ウで出来る
cmの直角三角形×4と一辺1cmの正方形ウで出来る
一辺 cmの正方形 ∴ 5cm2
cmの正方形 ∴ 5cm2
(2)2番目に大きな正方形は、1辺2cmの正方形
※(ア+イ)×4 または (ア+イ)×3+ウ
∴ 4cm2
解答・その3
(ペンネ-ム:三角定規)
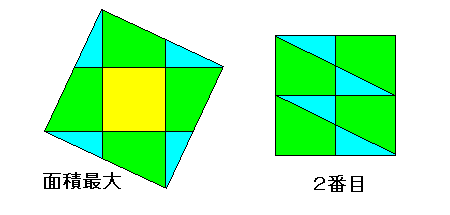
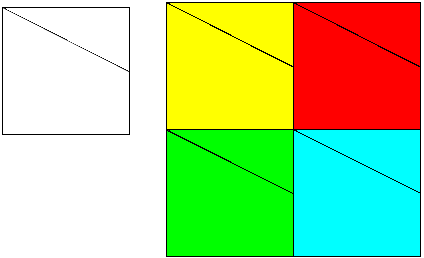
・面積最大のもの=左図 … 与えられたピースをすべて使っているから面積最大です。
・面積2番目のもの=右図 … ピースをどれか除いて正方形で次に面積が大きいのはこれです。
解答・その4
(ペンネ-ム:teki)
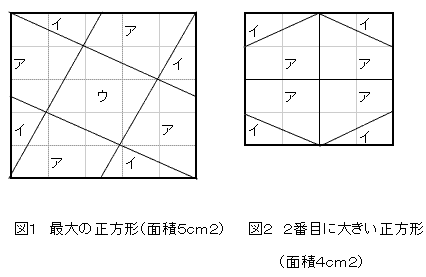
2番目に大きな正方形は簡単です。
アとイを4枚ずつ使って、面積が4cm2(つまり1辺が2cm)の正方形を作れば
いいわけです。(または、ア、イ各々3枚、ウ1枚でも可。)
さて、与えられた図形全てを利用して正方形が作れたら、これが最大となるわけ
ですが、全ての図形の面積の合計は5cm2です。
面積5cm2の正方形を作るには、
1辺 cmを作る必要があるわけですが、こ
れは以前に面積5分の1の問題で出てましたよね。
cmを作る必要があるわけですが、こ
れは以前に面積5分の1の問題で出てましたよね。
解答・その5
 (ペンネ-ム:杖のおじさん)
(ペンネ-ム:杖のおじさん)
答え
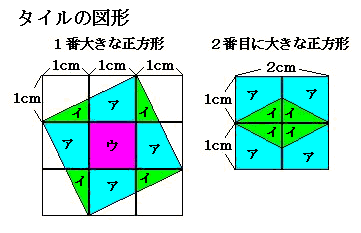
各タイルの面積は次の通りです。
ア は0.75cm2×4=3cm2
イ は0.25cm2×4=1cm2
ウ は1cm2×1=1cm2
合計 ア+イ+ウ=5cm2
従って
○ 一番大きな正方形は面積5㎝2、一辺が√5cmになります。
使うタイルはアが4枚、イが4枚、ウが1枚、全部使います。
○ 二番目に大きな正方形は面積4cm2、一辺が2cmになります。
使うタイルはアが4枚とイが4枚を使います。
解答・その6
(ペンネ-ム:巷の夢)
それぞれのタイルの面積はアが3/4、イが1/4そしてウが1であるから、
全部のタイルを加えると面積は5となる。因って、
面積が5から1の正方形を作ることが出来るか否かを検証すれば良い。
この場合、面積は整数でなくとも良いが、
使える図形の長さが /2、1、1/2の3種類で、
9個のみであるため19/4~17/4(最大である5と次の4の間)のような面積を作ることは出来ない。
そこで整数のみ考えれば良い。
/2、1、1/2の3種類で、
9個のみであるため19/4~17/4(最大である5と次の4の間)のような面積を作ることは出来ない。
そこで整数のみ考えれば良い。
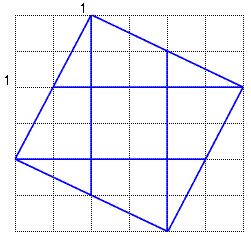
(1)まず5であるが、長さが の正方形をつくれるか否かにかかるので考えてみると、
下図の様な1と2の長さを持ち、斜辺の長さが
の正方形をつくれるか否かにかかるので考えてみると、
下図の様な1と2の長さを持ち、斜辺の長さが の直角三角形を4個
重ねればよいことが分かる。因って以下の様になる。
の直角三角形を4個
重ねればよいことが分かる。因って以下の様になる。

(2)次に大きいのは面積4であり、これは長さが2の正方形をつくれるか否かにかかるが、
明らかに可能である。いろいろ出来るが一例としてあげると、以下の様になる。
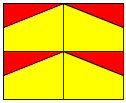
即ち、求める面積は5と4である。
解答・その7
(ペンネ-ム:のっこん)
単位を省略する
(1)ア4、イ4、ウ1の面積合計は5
よって一辺が の正方形を作れば面積は最大となる
の正方形を作れば面積は最大となる
アとイを並べて斜辺が の直角三角形を作る
の直角三角形を作る
この4つの直角三角形を斜辺が外側にくるように並べ、中にウを置けばよい
(2)ア4、イ3、ウ1の面積合計は19/4
一辺が(√19)/2 の正方形を作ることはできない
(3)ア3、イ4、ウ1の面積合計は17/4
一辺が(√17)/2 の正方形を作ることはできない
(4)ア4、イ4の面積合計は4(ア3、イ3、ウ1でも同じ)
よって一辺が2の正方形を作れば面積は2番目に大きくなる
アとイを並べて1×1の正方形を作る
この4つの正方形を2×2に並べればよい
解答・その8
(ペンネ-ム:バルタン星人)
最大5、2番目4
各図形の辺は、0.5、1、 /2の3種類
/2の3種類
面積は、ア:0.75、イ:0.25、ウ:1
また合計の総面積は5、1辺が の正方形を作れればそれが最大
の正方形を作れればそれが最大
アとイを組合せ、斜辺が の直角三角形を作り、
その斜辺を正方形の4辺に配置し、真ん中にウをはめ込むと最大の正方形。
の直角三角形を作り、
その斜辺を正方形の4辺に配置し、真ん中にウをはめ込むと最大の正方形。
次に大きい可能性は1辺が(1+ /2)だが面積が
9/4+
/2)だが面積が
9/4+ となり、
となり、
 の面積はありえない。
その次は1+1=2 アとイを組合せ1辺1の正方形を作り
この4個を組み合わせると2×2ができる。
の面積はありえない。
その次は1+1=2 アとイを組合せ1辺1の正方形を作り
この4個を組み合わせると2×2ができる。

解答・その9
(ペンネ-ム:転位反応)
全てのタイルの面積の合計は5cm2なので、求める正方形の一辺の長さは
最大で (2)二番目に大きな正方形:一辺の長さ2
例えば次のような並べ方があり、使用しないタイルは1又は2個
(ペンネ-ム:夜ふかしのつらいおじさん) 面積が一番大きな正方形は、アとイを次のように組合わせて全部使います。 面積が二番目に大きな正方形はアとイを次のように組合わせて使います。(ウは使いません)
タイル9枚の面積は、ア×4+イ×4+ウ=5 です。
だから、1辺の長さを これらの面積をもつ正方形の1辺の長さは、 この中で可能なのは、1辺の長さが2のものです。 (ペンネ-ム:T_Tatekawa) まず,全てのタイルの面積の和を求めてみます. (ペンネ-ム:kohji) ア、イ、ウの面積はそれぞれ1、0.75、0.25 (cm2) で、全部で5 (cm2) (ペンネ-ム:長崎島原 かがみ) (1)面積が最大の正方形 (2)面積が2番目に大きい正方形 (ⅰ) (2)<別解> (ⅰ) 1個取り除く場合 (ⅱ) 2個取り除く場合 (ⅲ) 3個取り除く場合 (ⅳ) ウを1個取り除いた場合 面積最大の正方形を作るには、すべてのタイルを使えばいいので、面積が5㎝2、
つまり1辺が  である。
である。
従って、各タイルの辺の長さの組合せから、二番目は
1+1/2・ 、
三番目は2の可能性が考えられるが、1+1/2・
、
三番目は2の可能性が考えられるが、1+1/2・ の場合は正方形の面積が無理数となるので不適当である。
の場合は正方形の面積が無理数となるので不適当である。
検証を行うと以下の通り。
全てのタイルを使用する
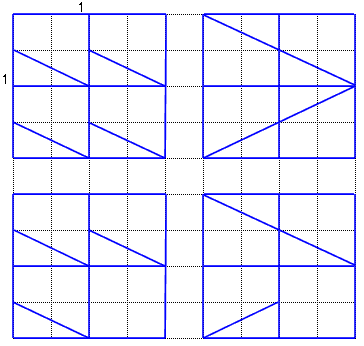
解答・その10

 にできればよいことになりま
にできればよいことになりま
二番目に大きな正方形の大きさを考えるために、「5」からタイルの面積を引いていきます。
すると、
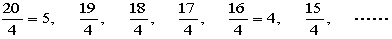
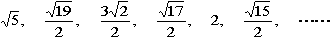
解答・その11
ア:(1cm+0.5cm)*1cm /2 = 0.75 cm2
イ:0.5cm * 1cm /2 = 0.25 cm2
ウ:1cm * 1cm = 1cm2
より
0.75 * 4 + 0.25 * 4 + 1 = 5 cm2
です.そこで出来うる最大の正方形の面積は 5 cm2 です.
次に正方形の一辺の長さに着目します.
5 = 1*1 + 2*2
であることから,三平方の定理よりアとイをくっつけた
三角形を考えるとその斜面の長さは  cm となります.
cm となります.
この三角形を四つ並べると,中心に1辺の長さが1cm の
正方形の空洞が出来ます.
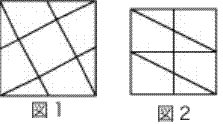
ここにウの正方形を入れれば完成です(図1)
二番目に大きい正方形を考えます.
タイルの各辺の長さは 1cm, 0.5cm,  /2 cm なので,
この組み合わせの二乗がうまく合わないと正方形が出来ません.
面積は 0.25cm2 刻みで調整できます.
/2 cm なので,
この組み合わせの二乗がうまく合わないと正方形が出来ません.
面積は 0.25cm2 刻みで調整できます.
4.75 = 19/4 (イを1個使わない)
4.5 = 9/2 (イを2個使わない)
4.25 = 17/4 (アを1個使わないか,イを3個使わない)
この辺りは出来そうにありません.
4 = 22
これは簡単に出来ます.いくつか解がありますが,
ウを使わなければ出来ます(図2)
解答・その12
ア、イ、ウの各辺の長さは /2、1、0.5(cm)のいずれかなので、
正方形の一辺の長さは p+
/2、1、0.5(cm)のいずれかなので、
正方形の一辺の長さは p+ q (p,qは有理数) と表せる。
よって面積は {p+
q (p,qは有理数) と表せる。
よって面積は {p+ q}2=(p2+5q2)+
q}2=(p2+5q2)+ (2pq)
また正方形の面積は1、0.75、0.25 (cm2) のタイルがいくつか合わさったものなので有理数である。
よって p2+5q2,2pq は有理数なので 2pq=0⇔p=0∨q=0
(2pq)
また正方形の面積は1、0.75、0.25 (cm2) のタイルがいくつか合わさったものなので有理数である。
よって p2+5q2,2pq は有理数なので 2pq=0⇔p=0∨q=0
p=0のとき
長さが無理数のタイルの辺は  /2 (cm) の辺が8本あるだけなので、
面積は {(
/2 (cm) の辺が8本あるだけなので、
面積は {( )/2}2,{2*
)/2}2,{2* /2}2 すなわち 1.25,5 (cm2) になり得る。
/2}2 すなわち 1.25,5 (cm2) になり得る。
q=0のとき
長さが有理数のタイルの辺は 1 または 0.5 (cm) なので、
正方形の一辺の長さは0.5 (cm) の自然数倍となる。
22<5<(2.5)2 なので、面積は高々 4 (cm2) である。
図より面積が5、4 (cm2) の正方形は確かに存在するので、
面積が一番大きな正方形と二番目に大きな正方形の一つはそれぞれ図のa,bである。
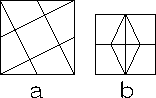
解答・その13
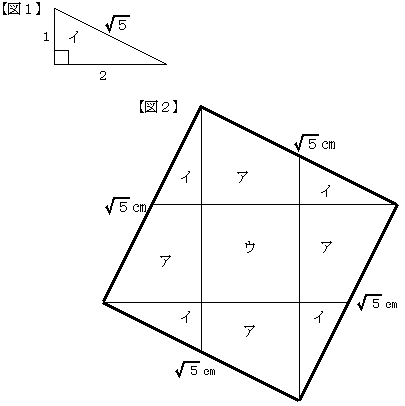
面積の合計が5㎝2だから、1辺が
 ≒2.236の正方形を考えればよい。
≒2.236の正方形を考えればよい。
1㎝2の平方形の周りに、左の図1の直角三角形を4個敷
き詰めればよい。
したがって、面積が最大である正方形は下の図2である。
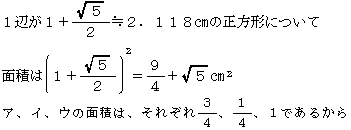
どんなに組み合わせても正方形はできない。
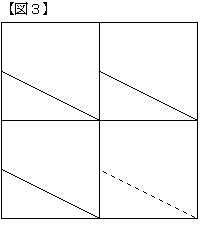 (ⅱ) 1辺が2㎝の正方形について 図3のような正方形ができる。
以上によって、2番目に面積が大きい正方形は 面積4㎝2の正方形である。
(ⅱ) 1辺が2㎝の正方形について 図3のような正方形ができる。
以上によって、2番目に面積が大きい正方形は 面積4㎝2の正方形である。
面積5㎝2から「図形イ」を1~3個まで取り除いた場合を考える。

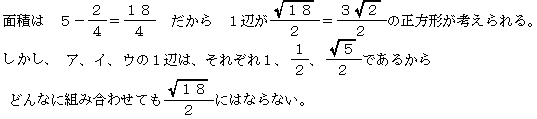


面積は5-1=4 だから 1辺が2の正方形が考えられる。右図のように正方形ができる。
正解者
teki
T_Tatekawa
バルタン星人
巷の夢
スモークマン
夜ふかしのつらいおじさん
転位反応
のっこん
長崎島原 かがみ
オヤジ
杖のおじさん
kohji
三角定規
まとめ
 の正方形になります。
この長さを見つけられらば、答えにたどりつけますね。
の正方形になります。
この長さを見つけられらば、答えにたどりつけますね。
2番目に大きい正方形の面積は、4㎝2ですが、厳密には、
これが確かに、2番目に大きい正方形であるということを示す必要があります。
つまり、面積が5㎝2より小さく、4㎝2より大きい正方形は作れないということです。
また、面積4㎝2の正方形の作り方は、いろいろなパターンがあります。
 top
top