侾俁俀丏愇傪庢傝弌偡栤戣
侾丆俀丆丒丒丒丆侾侽侽偺斣崋偺偮偄偨侾侽侽屄偺敔偑偁傝丄
偦傟偧傟偺敔偵斣崋偲摨偠悢偺愇偑擖偭偰偄傞丅
侾夞偺憖嶌偱丄偙偺拞偺偄偔偮偐偺敔傪慖傃丄
偦傟傜偡傋偰偐傜摨偠悢偺愇傪庢傝弌偡偙偲偑偱偒傞傕偺偲偡傞丅
偡傋偰偺敔傪嬻偵偡傞偺偵嵟掅壗夞偺憖嶌傪偡傟偽傛偄偱偡偐丅
栤戣偺弌揟
僕儏僯傾悢妛僆儕儞僺僢僋
悢妛僆儕儞僺僢僋嵿抍曇
婽彂朳敪峴
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗僆儎僕乯
丂傗傝曽偑晄柧側偺偱丄嬶懱揑偵傗傝傑偟偨丅
乮侾乯侾夞栚偵丂俆侾敔偐傜丂俆侽屄偢偮庢傝弌偡丅
丒乷侾屄乸丆乣乷係俋屄乸丂丒丒俀慻
丒乷俆侽屄乸丂丂丂丂丂丂丂丒丒侾慻
丒乽侽屄乿丂丂丂丂丂丂丂丂丒丒侾敔
乮俀乯俀夞栚偵丂俆侾敔偐傜丂俀俆屄偢偮庢傝弌偡丅
丒乷侾屄乸丆乣乷俀係屄乸丂丒丒係慻
丒乷俀俆屄乸丂丂丂丂丂丂丂丒丒侾慻
丒乽侽屄乿丂丂丂丂丂丂丂丂丒丒俁敔
乮俁乯俁夞栚偵丂係俋敔偐傜丂侾俁屄偢偮庢傝弌偡丅
丒乷侾屄乸丆乣乷侾侾屄乸丂丒丒俉慻
丒乷侾俀屄乸丂丂丂丂丂 丂丒丒俆慻
丒乽侽屄乿丂丂丂丂丂丂丂 丒丒俈敔
乮係乯係夞栚偵丂俆俁敔偐傜丂俇屄偢偮庢傝弌偡丅
丒乷侾屄乸丆乣乷俆屄乸丂 丒丒侾俇慻
丂
丒乷俇屄乸丂丂丂丂丂 丂丒丒俆慻
丒乽侽屄乿丂丂丂丂丂丂丂丒丒侾俆敔
乮俆乯俆夞栚偵丂俆俁敔偐傜丂俁屄偢偮庢傝弌偡丅
丒乷侾屄乸丆乣乷俀屄乸丂丒丒俁俀慻
丒乷俁屄乸丂丂丂丂丂 丂丒丒俆慻
丒乽侽屄乿丂丂丂丂丂丂 丒丒俁侾敔
乮俇乯俇夞栚偵丂俁俈敔偐傜丂俀屄偢偮庢傝弌偡丅
丒乷侾屄乸丂丂丂丂丂 丂丒丒俁俈敔
丒乽侽屄乿丂丂丂丂丂 丂丒丒俇俁敔
乮俈乯俈夞栚偵丂俁俈敔偐傜丂侾屄偢偮庢傝弌偡丅
丒乽侽屄乿丂丂丂丂丂 丂丒丒侾侽侽敔
丂丂丂亪丂俈夞
夝摎丒偦偺2
乮儁儞僱亅儉丗岼偺柌乯
- 傑偢1乣100傑偱偺敔傪2僌儖乕僾偵暘偗傞丅
懄偪丄1乣50偲51乣100偲偡傞丅偦偟偰屻幰偺僌儖乕僾偐傜奺乆50屄偯偮庢傝弌偡丅
偡傞偲屻幰偺僌儖乕僾傕1乣50偲側傞丅
- 師偵1乣50傑偱偺敔傪2僌儖乕僾偵暘偗傞丅懄偪丄1乣25偲26乣50偲偡傞丅
偦偟偰屻幰偺僌儖乕僾偐傜奺乆25屄偯偮庢傝弌偡丅偡傞偲屻幰偺僌儖乕僾傕1乣25偲側傞丅
- 峏偵1乣25傑偱偺敔傪2僌儖乕僾偵暘偗傞丅懄偪丄1乣12偲13乣25偲偡傞丅
偦偟偰屻幰偺僌儖乕僾偐傜奺乆13屄偯偮庢傝弌偡丅偡傞偲屻幰偺僌儖乕僾偼0乣12偲側傞丅
- 偙傟埲崀偼忋婰偲摨條側憖嶌傪孞傝曉偡丅
懄偪丄0乣6偲7乣12偦偟偰屻幰偺僌儖乕僾偐傜奺乆6屄偯偮庢傝弌偡丅偡傞偲屻幰偺僌儖乕僾偼1乣6偲側傞丅
- 0乣6偺敔傪0乣3偲4乣6偵暘偗丄屻幰偺僌儖乕僾偐傜奺乆3屄偯偮庢傝弌偡丅
偡傞偲屻幰偺僌儖乕僾偼1乣3偲側傞丅
- 偦偙偱丄0乣3偺敔傪0乣1偲2乣3偵暘偗丄屻幰偺僌儖乕僾偐傜奺乆2屄偯偮庢傝弌偡丅
偡傞偲屻幰偺僌儖乕僾偼0乣1偲側傞丅
- 偙偙偱慡偰偺敔偺拞恎偼0側偄偟1屄偲側偭偨偺偱丄1屄庢傝弌偣偽丄慡偰偺敔偼嬻偲側傞丅
夝摎丒偦偺3
乮儁儞僱亅儉丗偺偭偙傫乯
a 屄偺愇偑擖偭偨敔偑2屄偁偭偰傕丄a 屄偺愇偑擖偭偨敔偑1屄偁傞偺偲摨偠偱偁傞
偙偺帪丄敔偺悢偼1屄尭偭偨偙偲偵側傞丅偙偺傛偆偵峫偊偰敔偺悢傪尭傜偟偰偄偔丅
(1)1乣2n 偺帪
丂侾夞偺憖嶌偱尭傜偡偙偲偑偱偒傞敔偺悢偺嵟戝偼n 屄偱偁傞
(2)1乣2n-1 偺帪丂
丂侾夞偺憖嶌偱尭傜偡偙偲偑偱偒傞敔偺悢偺嵟戝偼n 屄偱偁傞
丒侾夞栚
丂丂50乣100偁傞偄偼51乣100傪慖傃丄偡傋偰偐傜50屄庢傝弌偡
丂丂丒丒敔偺悢偼50屄尭傞丒丒1乣50偑巆偭偨偲峫偊偰傛偄
丒俀夞栚
丂丂25乣50偁傞偄偼26乣50傪慖傃丄偡傋偰偐傜25屄庢傝弌偡
丂丂丒丒敔偺悢偼25屄尭傞丒丒1乣25偑巆偭偨偲峫偊偰傛偄
丒俁夞栚
丂丂13乣25傪慖傃丄偡傋偰偐傜13屄庢傝弌偡
丂丂丒丒敔偺悢偼13屄尭傞丒丒1乣12偑巆偭偨偲峫偊偰傛偄
丒係夞栚
丂丂6乣12偁傞偄偼7乣12傪慖傃丄偡傋偰偐傜6屄庢傝弌偡
丂丂丒丒敔偺悢偼6屄尭傞丒丒1乣6偑巆偭偨偲峫偊偰傛偄
丒俆夞栚
丂丂3乣6偁傞偄偼4乣6傪慖傃丄偡傋偰偐傜3屄庢傝弌偡
丂丂丒丒敔偺悢偼3屄尭傞丒丒1乣3偑巆偭偨偲峫偊偰傛偄
丒俇夞栚
丂丂2偲3傪慖傃丄奺乆偐傜2屄庢傝弌偡
丂丂丒丒敔偺悢偼2屄尭傞丒丒1偩偗偑巆偭偨偲峫偊偰傛偄
丒俈夞栚
丂丂1偐傜1屄庢傝弌偡
忢偵敔傪嵟戝尷尭傜偟偰偒偨偐傜丄俈夞偺憖嶌偑嵟彫偱偁傞
丒侾夞栚
丂丂51乣100傪慖傃丄偡傋偰偐傜51屄庢傝弌偟偰傕傛偄
丒俀夞栚
丂丂26乣50傪慖傃丄偡傋偰偐傜26屄庢傝弌偟偰傕傛偄
丒係夞栚
丂丂7乣12傪慖傃丄偡傋偰偐傜7屄庢傝弌偟偰傕傛偄
丒俆夞栚
丂丂4乣6傪慖傃丄偡傋偰偐傜4屄庢傝弌偟偰傕傛偄
夝摎丒偦偺4
乮儁儞僱亅儉丗偙傑偭偨僐乯
堦搙偵偱偒傞偩偗懡偔偺敔偐傜摨偠悢傪庢傝弌偣傞偲傛偄丅
崻嫆偼側偄偑嵟戝100屄偺敿暘偺50屄傪傑偢庢傝弌偡丅
1夞栚丒丒丒50屄庢傝弌偡丅
1乣49偺敔偐傜偼庢傝弌偣側偄偺偱偦偺傑傑丅
50乣100偺敔偐傜偼偦傟偧傟50屄偢偮庢傝弌偡丅
偦傟偧傟丂0, 1, 2, ...., 49, 50屄巆傞丅
偙傟傪傑偲傔傞偲
1乣49屄巆偭偰偄傞敔偑偦傟偧傟2敔丄50屄巆偭偰偄傞敔偑1敔丅
2夞栚丒丒丒25屄庢傝弌偡丅
1乣24屄巆偭偰偄傞敔偐傜偼庢傝弌偣側偄偺偱偦偺傑傑丅
25乣50屄巆偭偰偄傞敔偐傜偼偦傟偧傟25屄偢偮庢傝弌偡丅
偦傟偧傟丂0, 1, 2, ...., 24, 25屄巆傞丅
偙傟傪傑偲傔傞偲
1乣24屄巆偭偰偄傞敔偑偦傟偧傟4敔丄25屄巆偭偰偄傞敔偑1敔丅
3夞栚丒丒丒13屄庢傝弌偡丅
1乣12屄巆偭偰偄傞敔偐傜偼庢傝弌偣側偄偺偱偦偺傑傑丅
13乣25屄巆偭偰偄傞敔偐傜偼偦傟偧傟13屄偢偮庢傝弌偡丅
偦傟偧傟丂0, 1, 2, ...., 11, 12屄巆傞丅
偙傟傪傑偲傔傞偲
1乣11屄巆偭偰偄傞敔偑偦傟偧傟8敔丄12屄巆偭偰偄傞敔偑5敔丅
4夞栚丒丒丒6屄庢傝弌偡丅
1乣5屄巆偭偰偄傞敔偐傜偼庢傝弌偣側偄偺偱偦偺傑傑丅
6乣12屄巆偭偰偄傞敔偐傜偼偦傟偧傟6屄偢偮庢傝弌偡丅
偦傟偧傟丂0, 1, 2,..5, 6屄巆傞丅
偙傟傪傑偲傔傞偲
1乣5屄巆偭偰偄傞敔偑偦傟偧傟16敔丄6屄巆偭偰偄傞敔偑5敔丅
5夞栚丒丒丒3屄庢傝弌偡丅
1乣2屄巆偭偰偄傞敔偐傜偼庢傝弌偣側偄偺偱偦偺傑傑丅
3乣6屄巆偭偰偄傞敔偐傜偼偦傟偧傟3屄偢偮庢傝弌偡丅
偦傟偧傟丂0, 1, 2, 3屄巆傞丅
偙傟傪傑偲傔傞偲
1乣2屄巆偭偰偄傞敔偑偦傟偧傟32敔丄3屄巆偭偰偄傞敔偑5敔丅
6夞栚丒丒丒2屄庢傝弌偡丅
1屄巆偭偰偄傞敔偐傜偼庢傝弌偣側偄偺偱偦偺傑傑丅
2乣3屄巆偭偰偄傞敔偐傜偼偦傟偧傟3屄偢偮庢傝弌偡丅
偦傟偧傟丂0, 1屄巆傞丅
偙傟傪傑偲傔傞偲
1屄巆偭偰偄傞敔偑37敔丅
7夞栚丒丒丒偡傋偰偺敔偐傜1屄偢偮庢傝弌偡丅
偙傟偱偡傋偰偺敔偺嬍偑側偔側傞丅
埲忋傛傝丄7夞丅
夝摎丒偦偺5
乮儁儞僱亅儉丗Toru乯
媮傔傞悢傪f(100)偲偡傞
丂愇偺悢偑摨偠敔偼侾偮偲峫偊偰傕傛偄偐傜丄巆傝偺愇偺悢偺庬椶偑側傞傋偔彮側偔
側傞傛偆偵峫偊傞丅
丂係俋敔埲壓偐傜庢傝弌偟偨応崌偼丄巆傝偺敔傪峫偊傟偽丄巆傝偺庬椶偼俆侾埲忋偲
側傞丅俆俀敔埲忋偐傜庢儕偩偟偨応崌傕丄庢傝弌偟偨敔偺偆偪巆傝侽偺傕偺傪彍偄偰丄
巆傝偺庬椶偼傗偼傝俆侾庬椶埲忋偵側傞丅
丂俆侽敔丄俆侾敔偐傜庢傝弌偟偨帪偼摨條偵俆侽庬椶埲忋偵偟偐偱偒側偄偑丄
1)50屄偢偮50-100偐傜偁傞偄偼51屄偢偮51-100偐傜偲傞偲丄妋偐偵
1,2,3,------49,1,2,--------50偲愇偺悢偼俆侽庬椶偲側傞丅
丂偙偺庢傝曽偑嵟慞偱偺偙傝偼丄f(50)丅
丂
丂埲壓摨條偵
2)25屄偢偮25-50偐傜偁傞偄偼26屄偢偮26-50偐傜偲傝偩偟偰丂
偺偙傝f(25)
3)13屄偢偮13-25偐傜庢傝弌偟偰丂
偺偙傝f(12)
4)6屄偢偮6-12偁傞偄偼7屄偢偮7-12偐傜庢傝弌偟偰
偺偙傝f(6)
5)3屄偢偮3-6偁傞偄偼4屄偢偮4-6偐傜庢傝弌偟偰
偺偙傝f(3)
6)2屄偢偮2-3偐傜庢傝弌偟偰
偺偙傝f(1)
7)侾屄偢偮慡偰偐傜庢傝弌偟偰廔傢傝
偲偄偆偙偲偱俈夞
夝摎丒偦偺6
乮儁儞僱亅儉丗揮埵斀墳乯
峫偊曽傪帵偡偨傔偵丄敔偺悢傪侾侽屄偲偟丄偦傟偧傟偺敔偺拞偺愇傪
壓恾偺傛偆偵柾幃揑偵暲傋偰昞偡偙偲偵偡傞丅
戣堄偺憖嶌偺夞悢偼丄敔偵擖偭偰偄傞愇偺悢偑嵟傕懡偄傕偺偵埶懚
偡傞偺偱丄堦夞偺憖嶌偛偲偵丄偦偺愇偺悢傪嵟彮偲偡傞庢傝曽傪孞傝
曉偣偽椙偄偙偲偵側傞丅
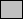 丂
傪敔偐傜庢傝弌偡愇偲偡傞偲丄敔偺拞偵偼嵟懡偱俆屄偺愇偑巆傞丅
丂
傪敔偐傜庢傝弌偡愇偲偡傞偲丄敔偺拞偵偼嵟懡偱俆屄偺愇偑巆傞丅
恾偱偼擇偮偺敔偵俆屄偺愇偑巆偭偰偄傞応崌傪帵偟偰偄傞偑丄偳傫側
庢傝弌偟曽傪偟偰傕丄彮側偔偲傕傂偲偮偺敔偵偼俆屄偺愇偑巆傞丅
偙偙偱偼丄愇偑俆屄擖偭偨敔偺悢偼栤戣偲偼側傜側偄丅
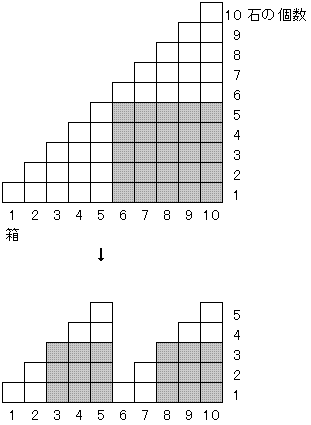
埲壓丄摨條偺峫偊曽偱憖嶌傪峴偊偽傛偄丅
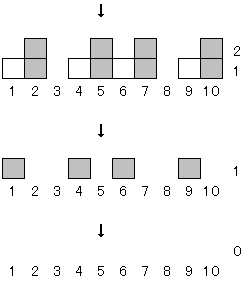
廬偭偰丄侾侽屄偺応崌偺憖嶌偼丄嵟掅係夞偲側傞丅
偝偰丄慡偔摨條側峫偊曽偱丄敔偑侾侽侽屄偺応崌傪峫偊傞
敔偵擖偭偰偄傞嵟懡偺愇偺屄悢偺曄壔偼丄
丂丂丂100仺50仺25仺12仺6仺3仺1仺0
憖嶌偼嵟掅俈夞偲側傞丅
夝摎丒偦偺7
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊
俈夞偺憖嶌傪偡傟偽椙偄偱偡丅
敔偺拞偵偼俆侽俆侽屄偺愇偑擖偭偰偄傑偡丅
丂丂丂乮乮侾亄侾侽侽乯亊侾侽侽乯亖俆侽俆侽
侾乣侾侽侽傑偱偺敔偺斣崋傪俀恑朄偱晅斣偟傑偟偨丅
偦偆偡傞偲侾侽侽斣栚偺敔偼侾侾侽侽侾侾侽偱俈寘傪昁梫偲偟傑偡丅
敔傪慖傇帪偼奺寘傪慖傃俀恑朄偵傛傞侾偲昞帵偝傟偰偄傞傕偺傪慖傃偦偺寘偺悢偩偗愇傪庢傝弌偟傑偡丅
侾夞栚偼侾寘栚偑侾偱偁傞俆侽屄偺敔傪慖傃奺敔偐傜侾屄丄崌寁俆侽屄傪庢傝弌偡丅
俀夞栚偼俀寘栚偑侾偱偁傞俆侽屄偺敔傪慖傃奺敔偐傜俀屄丄崌寁侾侽侽屄傪庢傝弌偡丅
俁夞栚偼俁寘栚偑侾偱偁傞係俋屄偺敔傪慖傃奺敔偐傜係屄丄崌寁侾俋俇屄傪庢傝弌偡丅
係夞栚偼係寘栚偑侾偱偁傞係俉屄偺敔傪慖傃奺敔偐傜俉屄丄崌寁俁俉係屄傪庢傝弌偡丅
俆夞栚偼俆寘栚偑侾偱偁傞係俉屄偺敔傪慖傃奺敔偐傜侾俇屄丄崌寁俈俇俉屄傪庢傝弌偡丅
俇夞栚偼俇寘栚偑侾偱偁傞俁俈屄偺敔傪慖傃奺敔偐傜俁俀屄丄崌寁侾侾俉係屄傪庢傝弌偡丅
俈寘栚偼俈寘栚偑侾偱偁傞俁俈屄偺敔傪慖傃奺敔偐傜俇係屄丄崌寁俀俁俇俉屄傪庢傝弌偡丅
崌寁俆侽俆侽屄偺愇傪慡晹庢傝弌偡偙偲偑弌棃傑偟偨丅廬偭偰俈夞偺憖嶌偱嬻偵側傞丅
夝摎丒偦偺8
乮儁儞僱亅儉丗嶰妏掕婯乯
侾乣侾侽侽 傪俀恑悢昞婰偟丆嵟壓埵價僢僩偐傜奺價僢僩偵乪侾乫偑棫偭偰偄傞敔偐傜
侾丆俀丆係丆俉丆侾俇丆俁俀丆俇係屄偢偮庢傟偽傛偄丅
偡側傢偪丆埲壓偺庤弴偱敔傪慖傃愇傪庢傟偽丆俈夞偱庢傝恠偔偡偙偲偑偱偒傞丅
(1) 愇悢偑婏悢屄偺敔乮50屄偁傞乯偐傜侾屄偢偮庢傝弌偡丅丂丂丂丂丂丂丂丂丂仺
愇悢偼偡傋偰嬼悢偵
(2) 愇悢傪 係 偱妱傞偲 俀 梋傞敔乮50屄偁傞乯偐傜 俀 屄偢偮庢傝弌偡丅仺
愇悢偼偡傋偰 係 偺攞悢偵
(3) 愇悢傪 俉 偱妱傞偲 係 梋傞敔乮49屄偁傞乯偐傜 係 屄偢偮庢傝弌偡丅仺
愇悢偼偡傋偰 俉 偺攞悢偵
(4) 愇悢傪 侾俇 偱妱傞偲 俉 梋傞敔乮48屄偁傞乯偐傜 俉 屄偢偮庢傝弌偡丅仺
愇悢偼偡傋偰 侾俇 偺攞悢偵
(5) 愇悢傪 俁俀 偱妱傞偲 侾俇 梋傞敔乮48屄偁傞乯偐傜 侾俇 屄偢偮庢傝弌偡丅仺
愇悢偼 侽丆俁俀丆俇係丆俋俇 屄偵
(6) 愇悢偑 俁俀丆俋俇 屄偺敔乮37屄偁傞乯偐傜 俁俀 屄偢偮庢傝弌偡丅丂丂丂丂仺
愇悢偼 侽丆俇係 屄偵
(7) 愇悢偑 俇係 屄偺敔乮37屄偁傞乯偐傜 俇係 屄偢偮庢傝弌偡丅丂丂仼 庢傝恠偔偟
忋偺庢傝曽偱丆椺偊偽(4)偲(5)偼偦傟偧傟 係俉 屄偺敔偐傜愇傪庢傝弌偡偺偩偑丆
敔偑堎側傞偨傔丆偙傟傪侾夞偺憖嶌偵傑偲傔傞偙偲偼偱偒側偄丅
偡側傢偪丆愇偺庢傝弌偟傪俈夞傛傝彮側偔偡傞偙偲偼偱偒側偄丅
乵摎乶丂俈夞
夝摎丒偦偺9
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
摎偊丗俈夞
峫偊曽丗
侾侽侽庬椶傪尭傜偟偰偄偒丄嵟廔揑偵侽庬椶偵偡傞偲峫偊傞丅
庬椶傪尭傜偡嵟戝偼丄敿尭亄侾乮婏悢偺応崌丄侽偵偱偒傞偐傜乯
侾夞栚丗婏悢斣偐傜侾屄庢傞丅俀乣侾侽侽偺俆侽庬椶偵側傞丅
偙傟傪俀亊乮侾乣俆侽乯偲昞偡偲丄埲壓侾乣俆侽偺婏悢斣偐傜
侾乮俀亊侾偱俀屄偲傞乯庢傝丄偙傟傪孞傝曉偡偲
丂係亊乮侾乣俀俆乯
丂俉亊乮侾乣侾俀乯
丂侾俇亊乮侾乣俇乯
丂俁俀亊乮侾乣俁乯
丂俇係亊侾
丂侽
偲側傝俈夞偑嵟掅偺夞悢偲側傞丅
夝摎丒偦偺10
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯

偙偺栤戣偼丄捈妏擇摍曈嶰妏宍偐傜偦偺嶰妏宍偵撪愙偡傞挿曽宍傪孞傝曉偟偰
偔傝敳偔嶌嬈偲帡偰偄傑偡丅
捈妏擇摍曈嶰妏宍偵撪愙偡傞挿曽宍偱柺愊偑嵟戝偱偁傞偺偼惓曽宍偺偲偒偱丄
偦偺惓曽宍偺柺愊偼丄傕偲偺捈妏嶰妏宍偺柺愊偺敿暘偱偡丅
塃偺恾偱惓曽宍傪偔傝敳偄偨偲偒丄彫偝側捈妏擇摍曈嶰妏宍偑巆傝傑偡丅
偙偺擇偮偺捈妏擇摍曈嶰妏宍偼崌摨偱丄偙偺擇偮偵摨偠偙偲傪孞傝曉偟傑偡丅
偙偺嶌嬈偑柍尷偵懕偒傑偡丅
愇偺応崌偵偼桳尷夞偱憖嶌偑廔傢傝傑偡丅
敔偺屄悢偑丄2n-1偺応崌偼揟宆揑偵偆傑偔偄偒傑偡丅
椺偊偽丄7屄乮n=3)偺応崌偼
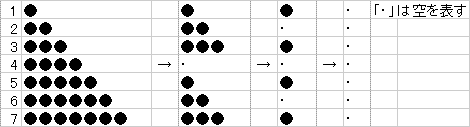
丂1夞栚丄乷4丆5丆6丆7乸偺敔偐傜4屄偺愇傪庢傞
丂2夞栚丄乷2丆3丆6丆7乸偺敔偐傜2屄偺愇傪庢傞
丂3夞栚丄乷1丆3丆5丆7乸偺敔偐傜1屄偺愇傪庢傞
偺傛偆偵丄3夞偺憖嶌偱嬻偵偱偒傑偡丅
偙偺憖嶌悢偑嵟掅偲偄偊傞偺偼丄偲傞愇偺屄悢偑嵟戝偲暘偐偭偰偄傞偐傜偱偡丅
偙偺條巕傪敔偵巆傞愇偺屄悢偱

偲昞偡偙偲偵偟傑偡丅
敔偺屄悢傪曄偊偰傒傑偡丅
椺偊偽8屄偲偟偰傒傑偡丅
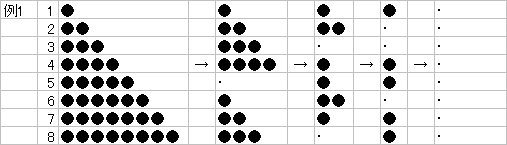
丂1夞栚丄乷5丆6丆7丆8乸偺敔偐傜5屄偺愇傪庢傞
丂2夞栚丄乷3丆4丆8乸偺敔偐傜3屄偺愇傪庢傞
丂3夞栚丄乷2丆6乸偺偼偙偐傜2屄偺愇傪庢傞
丂4夞栚丄乷1丆4丆5丆7丆8乸偺敔偐傜1屄偺愇傪庢傞
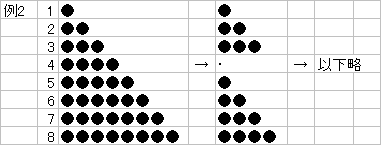
1夞栚傔偵乷4丆5丆6丆7丆8乸偺敔偐傜4屄偺愇傪庢偭偰傕椺1偲摨偠忬懺偵側傞
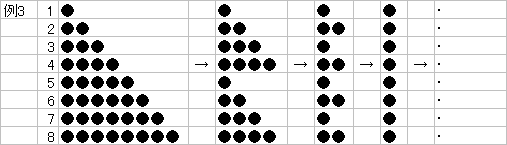
丂1夞栚丄乷5丆6丆7丆8乸偺敔偐傜4屄偺愇傪庢傞
丂2夞栚丄乷3丆4丆7丆8乸偺敔偐傜2屄偺愇傪庢傞
丂3夞栚丄乷2丆4丆6丆8乸偺敔偐傜1屄偺愇傪庢傞
丂4夞栚丄慡晹偺敔偐傜1屄偺愇傪庢傞
偺傛偆偵丄敿悢慜屻偺愇傪庢偭偰偄偗偽丄憖嶌悢偵堘偄偼側偄傛偆偱偡丅
偝偰丄100屄偺応崌偼師偺傛偆偵俈夞偺憖嶌偱偡傋偰偺敔偼嬻偵側傝傑偡丅

夝摎丒偦偺11
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
媡偐傜峫偊傞偲丄丄丄1 偼巆傞丅
偦偺慜偵2偼巆偭偰傞偺偱丄2傪庢傞偙偲傪峫偊傞丅
1+2=3
2, 偑巆偭偰偄偨偙偲偵側傞丅
4偼庢傜傟偰偄側偄偲偄偗側偄丅
1+4=5
1+2+4=7
2+4=6
偼巆偭偰偄偨偙偲偵側傞丅
8偼庢傜傟偰偄側偄偲偄偗側偄丅
埲壓摨條偵丄丄丄
16,32,64偑庢傜傟偰偄側偄偲偄偗側偄丅
偮傑傝丄100偐傜丄64,32,16,8,4,2,1 傪庢傟偽嬻偵側傞丅寁7夞昁梫丒丒丒偐側丠^^
夝摎丒偦偺12
乮儁儞僱亅儉丗T_Tatekawa乯
愇偺悢傪 2 恑悢偱昞偟偰峫偊偰傒傑偡丏
2*2 = 4 2*2*2 = 8 2*2*2*2 = 16 2*2*2*2*2 = 32 2*2*2*2*2*2 = 64 2*2*2*2*2*2*2 = 128 > 100側偺偱丆100 偼 2 偺 7 忔傛傝彫偝偄偱偡丏
椺偊偽 100 傪 2 恑悢偱昞偡偲丆乽1100100乿偵側傝傑偡丏
懠偺悢帤傕 2 恑悢偱昞偟丆慖傫偩寘偑 "1" 偵側偭偨偲偒偵愇傪 庢傝弌偡憖嶌傪偟偰偄偗偽偄偄偺偱偼側偄偱偟傚偆偐丏
嬶懱揑側憖嶌偼埲壓偺捠傝偱丆7 夞偱偡丏
1. 斣崋偑64埲忋偺敔傪慖傫偱丆愇傪64屄偢偮庢傝弌偡丏
2. 拞偵愇偑32屄埲忋巆偭偰偄傞敔偐傜丆32屄偢偮愇傪庢傝弌偡丏
3. 拞偵愇偑16屄埲忋巆偭偰偄傞敔偐傜丆16屄偢偮愇傪庢傝弌偡丏
4. 拞偵愇偑8屄埲忋巆偭偰偄傞敔偐傜丆8屄偢偮愇傪庢傝弌偡丏
5. 拞偵愇偑4屄埲忋巆偭偰偄傞敔偐傜丆4屄偢偮愇傪庢傝弌偡丏
6. 拞偵愇偑2屄埲忋巆偭偰偄傞敔偐傜丆2屄偢偮愇傪庢傝弌偡丏
7. 拞偵愇偑巆偭偰偄傞敔偐傜丆1屄偢偮愇傪庢傝弌偡丏
夝摎丒偦偺13
乮儁儞僱亅儉丗kiyo乯
夝摎
丂丂丂100亙64+32+16+8+4+2+1
丂丂丂(1+100)*100/2=5050=64*37+32*37+16*48+8*48+4*49+2*50+1*50
偟偨偑偭偰丄嵟彫俈夞丅
夝摎丒偦偺14
乮儁儞僱亅儉丗彲巌乯
偙偺栤戣偼丄2恑朄偲偦偺榓偱峫偊傑偟偨丅
曽朄丟20丄21丄22乧乧26偑彂偐傟偨斣崋偺敔偐傜偼丄
1夞偺巤峴偱慡晹偺愇傪庢傝弌偡偙偲偵偟丄偦傟埲奜偺斣崋偺敔偐傜偼丄忋婰偺悢偺慻傒
崌傢偣偱慡偰偺愇傪庢傝弌偟傑偡丅
椺偊偽3斣偺敔偺愇偼丄1斣(20)偺敔偲丄2斣(21)偺敔偐傜乧乧
50斣偺敔偺愇偼丄32斣偺敔(25)丄16斣偺敔(24)丄2斣(21)偺敔偐傜
愇傪庢傝弌偡娫偵丄敔偺拞偺愇傪慡偰庢傝偒傞偙偲偑弌棃傑偡丅
26亙100亙27偱偡偺偱丄嵟掅7夞偺巤峴偱100傑偱偺敔偐傜慡偰偺愇傪庢
傝弌偣傞偙偲偵側傝傑偡丅
夝摎丒偦偺15
乮儁儞僱亅儉丗teki乯
摎偊丂丂俈夞偺憖嶌偱壜擻偱偡丅
埲慜偵偁偭偨丄僶僀僫儕儕僒乕僠乮擇暘扵嶕乯偲摨條偺峫偊曽偑偱偒傑偡偹丅
敔偑俀値亅侾偐傜俀値亅侾傑偱偺応崌偼値夞偱壜擻偱偡丅
幚嵺偺傗傝曽偼丄敔偺屄悢偑婏悢偺応崌偼丄拞墰偺屄悢傪偦傟埲忋擖偭偰偄傞敔
偐傜丄嬼悢偺応崌偼丄N/俀亄侾屄埲忋擖偭偰偄傞敔偐傜丄偦傟偧傟庢傝弌偣傞偩偗
庢傝弌偡偙偲傪孞傝曉偣偽壜擻偱偡丅
偱丄俀俇亝侾侽侽亝俀俈亅侾丂側偺偱丄侾侽侽屄偺敔偺応崌偼丄
俈夞偑嵟抁庤悢偲側傝傑偡丅
幚嵺偵傗偭偰傒偨傢偗偱偼側偄偱偡偑丄懡暘偙傟偱偄偄偲巚偄傑偡丅
惓夝幰
| 僶儖僞儞惎恖 | kiyo | 栭傆偐偟偺偮傜偄偍偠偝傫 |
| T_Tatekawa | teki | 偺偭偙傫 |
| 偙傑偭偨僐 | Toru | 岼偺柌 |
| 揮埵斀墳 | 忨偺偍偠偝傫 | 僗儌乕僋儅儞 |
| 僆儎僕 | 嶰妏掕婯 | 彲巌 |
傑偲傔
侾侽侽庬椶偺悢偐傜丄愇傪庢傞偙偲偱丄庬椶悢傪敿暘丄敿暘偲尭傜偟偰偄偔偲偄偆
傾僀僨傿傾偺夝摎偑懡偐偭偨偱偡偹丅
丂丂丂俀俇亝侾侽侽亙俀俈
偱偡偐傜丄
嵟掅俈夞偲偄偆偙偲偵側傝傑偡丅
傑偨丄愇傪庢傞偐丄庢傜側偄偐丄俀捠傝偺慖戰巿偑偁傞傢偗偱偡偐傜丄
侾偐傜侾侽侽傑偱偺悢傪丄俀恑悢偱昞傢偟丄
寘偛偲偵丄侾偲昞婰偝傟偨悢偐傜丄偦偺悢傪庢偭偰偄偔偲偄偆
峫偊曽傕偱偒傑偡偹丅堦斣戝偒偄侾侽侽傪俀恑悢偱昞偡偲丄
丂丂丂侾侽侽亖1100100(2)
偲俈寘偱偡偐傜丄嵟掅俈夞昁梫偩偲偄偆偙偲偵側傝傑偡丅
 top
top