130.3nの和
3n(n≧0)の形をした1つ以上の相異なる整数の和として表される整数を小さい方から次ぎのように
並べる。
1,3,4,9,10,12,13,・・・
この数列の第100項を求めよ。
問題の出典
ジュニア数学オリンピック
数学オリンピック財団編
亀書房発行
答えと解説
解答・その1
(ペンネ−ム:こまったコ)
1, 3, 4, 9, 10, 13,
3n乗を小さいほうから1個以上組み合わせて数を作ることになる。
30を1個・・・1=21-1
30、31を各0か1個使う組み合わせ-2(どれも0個の組み合わせ、上の1通り)
=2x2-2=2通り・・・3, 4
ここまでにできた数は3つ = 22-1
30、31、32を各0か1個使う組み合わせ-2=2x2x2-4(どれも0の組み合わせ、上の3通り)=4通り・・9, 10, 12, 13
ここまでにできた数は7つ = 23-1
これを簡単にするために2n-1で100より小さい最大の数を求めると
26-1=63
27-1=127
127-63=64
63番目の数は1+3+9+27+81+243=364
64番目の数は36 = 729。
127番目の数は364+729=1093
100番目の数は729より大きく、1093より小さい。
100-64=36よりこの数列の36番目の数を729に足せばよい。
32番目の数は35 = 243
この数列の4番目の数は9なので 243+9=252
よってこの数列の36番目の数は252。
729 + 252 = 981
よってこの数列の100番目は981。
解答・その2
(ペンネ−ム:転位反応)
題意に沿って数列を書き下すと、
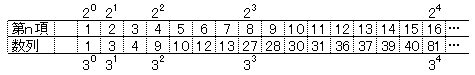
これから分かることは、
(1)3nは、第2n項である
(2)第2n項を第1項から第2n−1項のそれぞれに加えると、
第2n+1項から第2n+1−1項の数列となる
従って、第100項は、第64項(=26)と第128項(=27)の間にあるので、
第100項=第64項+第36項=第64項+第32項+第4項=26+25+22
と整理できる。よって、求める第100項は、 =36+35+32=981
解答・その3
(ペンネ−ム:まーや)
(答え)981
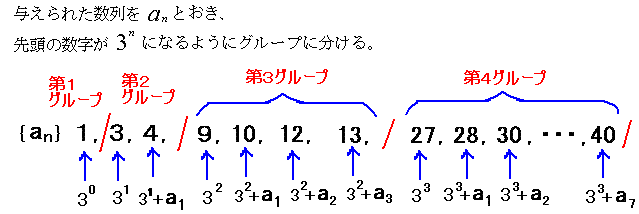
(方針)第100項が第何グループの何番目に来るかを求める。
各グループに含まれる数字の個数は、
第1グループ・・・1個
第2グループ・・・2個
第3グループ・・・4個
第4グループ・・・8個・・・となる。
第1〜6グループまでの数字の個数の和は
1+2+4+8+16+32=63個
100−63=37より、
第100項は第7グループの37番目。
解答・その4
(ペンネ−ム:巷の夢)
題意に従い数字を書き出してみると、
| 1 | 1 | ||||
| 2 | 3 | ||||
| 3 | 4 | ||||
| 4 | 9 | ||||
| 5 | 10 | ||||
| 6 | 12 | ||||
| 7 | 13 | ||||
| 8 | 27 | ||||
| 9 | 28 | ||||
| 10 | 30 | ||||
| 11 | 31 | ||||
| 12 | 36 | ||||
| 13 | 37 | ||||
| 14 | 39 | ||||
| 15 | 40 | ||||
| 16 | 81 | ||||
| 17 | 82 | ||||
| 18 | 84 | ||||
| 19 | 85 | ||||
| 20 | 90 | ||||
| 21 | 91 | ||||
| 22 | 93 | ||||
| 23 | 94 | ||||
| 24 | 108 | ||||
| 25 | 109 | ||||
| 26 | 111 | ||||
| 27 | 112 | ||||
| 28 | 117 | ||||
| 29 | 118 | ||||
| 30 | 120 | ||||
| 31 | 121 | ||||
| 32 | 243 |
これらの関係から下表の様な分析が出来る。
| 3の累乗 | 加算で出来る 数字の個数 | 増加数量 |
|---|---|---|
| 1 | 0 | 0 |
| 3 | 1 | 1 |
| 9 | 3 | 2 |
| 27 | 7 | 4 |
| 81 | 15 | 8 |
| 243 | 31 | 16 |
| 729 | 63 | 32 |
表の6行目までの数字を加えると63個である。
因って100番目の数は729と以前に出来た数を加えたものとなる。729が64番目であり、
更に加算で出来る36番目が全部の100番目にあたる。これは表から243+9であるから252となり、
729+252である981が求めるものである。
解答・その5
(ペンネ−ム:テレスとアリス)
数列を3nの和の形にしてみます。
そして、指数はそのままで、3を2に変えてみると「第何項」の「数」と一致します。
第1項 1=30 → 20=1
第2項 3=31 → 21=2
第3項 4=30+31 → 20+21=3
第4項 9=32 → 22=4
第5項 10=30+32 → 20+22=5
第6項 12=31+32 → 21+22=6
第7項 13=30+31+32 → 20+21+22=7
この手順を逆に進めて、第100項を求めます。
100=4+32+64=22+25+26 → 32+35+36=9+243+729=981
答えは、981 です。
解答・その6
(ペンネ−ム:バルタン星人)
答え:981
解法
3の(n−1)乗以下までの和は3のn乗を超えることはないので
異なる数の和が同じになることはない。
3の(n−1)乗までの和の個数は、各1,3,9・・・3n-1について使う
、使わないの2通りなので2のn乗。
但し、全て使わない場合はないので、2n−1
26=64、27=128なので、
100番目の和の中の最大数は36
100は2進法で1100100で表せるが
n桁目が1のものに3n-1が当てはまるので、
100番目は、
36+35+32
=729+243+9=981
解答・その7
(ペンネ−ム:オヤジ)
n番目の数を求めるのに、nを2進法で表現する
n=abcde(2) 但し{a,b,c,d,e}={0,1}とすると。
n番目の数=a×34+b×33+c×32+d×31
+e×30となる
従って
100=1100100(2)
求める100番目の数は、
1×36+1×35+0×34+0×33
+1×32+0×31+0×30
=729+243+0+0+9+0+0
=981
∴ 981
解答・その8
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
答 100項は981です。
3のN乗の整数の和の条件から3進法で数列を表現しますと
数列→1,3,4,9,10,12,13・ ・ ・ は
1,10,11,100,101,110,111・ ・ ・ となります。
1と0の数列だと判明い致しました。この数列はの100項は2進法の数列と同じです。
2進方の100項は1100100です。
3進法の100項は
1100100=36+35+32=729+243+9=981
です。
解答・その9
(ペンネ−ム:T_Tatekawa)
第1項:1 = 1 x 30
第2項:3 = 1 x 31 + 0 x 30
第3項:4 = 1 x 31 + 1 x 30
のように書いてみると,数列の番号を 2 進数表示して,
k 桁目の数字が 3k-1 の係数になっている事に気づくと
すぐできます.
100 = 64 + 32 + 4 = 26 + 25 + 22
ですので,第100項目は
36 + 35 + 2
= 729 + 243 + 9
= 981
です.
解答・その10
(ペンネ−ム:のっこん)
この問題は
「1g, 3g, 9g, 27g,・・の重りが1個ずつある。
これらの重りで作ることのできる重さを小さい順に並べた時、
100番目は何g か」と同じことである
作ることのできる重さは、3進法で0と1とを使った数
1, 10, 11, 100, 101, 110, 111, 1000, 1001, ・・
になるが、
これは2進法における自然数の表わし方と同じ
100を2進法で表わすと 1100100
これを3進法に読みかえて
729+243+9=981
解答・その11
(ペンネ−ム:nao)
問題になっている数列は、
1=30、
3=31、
4=30+30、
9=32、
10=30+32、
12=31+32、
13=30+31+32・・・
となっています。
すぐ気がつくことですが、3の階乗があるかないかであらわすと、最初の1は3の0
乗があるので1、つぎの3は3の0乗がなくて3の1乗があるので10、そのつぎの
4は3の0上と3の1乗があるので11・・・というように二進法で表せます。
100番目の数は、二進法であらわすと1100100です。問題の数は、
36+35+32=981
になります。
解答・その12
(ペンネ−ム:kohji)
以下 [P]m は Pをm進数で記したもの、すなわち
mは2以上の整数 かつ
P=mk-1*pk-1+mk-2*pk-1+…+m*p1+p0 (0≦pj<m pjは整数) のとき
[P]m=10k-1*pk-1+10k-2*pk-2+…+10*p1+p0
と定義する。
題意の数列をAnとする。
3k-1≦An<3k(kは自然数) のとき
An=a0+3*a1+…+3k-1*ak-1(aj=0 or 1)
と示せる。
またAnについて、n=1,2,3,…として上記の {ak-1,ak-2,…,a1,a0} を順に書くと
{1},{1,0},{1,1},{1,0,0},… となる。
すなわち
n=a0+2*a1+…+2k-1*ak-1
となる。
以上より
[An]3=[n]2
したがって、
[100]2=[26+25+22]2
=[36+35+32]3=[981]3
=[A100]3
⇔A100=981
解答・その13
(ペンネ−ム:teki)
答え 981
<解法>
100番目の数は、2進法で100を表した時の3進法への変換で出てきます。
(この辺の説明はきっとどなたかがやってくれると思いますので、サボっちゃいます(^^;;)
2進法で100は、
100(10進)=26+25+22=1100100(2進)
ですので、これを3進数として10進法に変換すると、
36+35+32=729+243+9=981
となります。105番目ならちょうど1000できりがいいのですが・・・・。
解答・その14
(ペンネ−ム:三角定規)
整数 N の2進法表記 bnbn-1…b1で bk =1 のときに 3k を加えていくことで,
題意を満たす数列が得られる。
整数 100 の2進法表記は 1100100 だから,求める数列の第100項は,
36+35+32=729+423+9=981 …[答]
解答・その15
(ペンネ−ム:Toru)
問題の数列
1,3,4,9,10,12,13---
を3進法であらわすと
1,10,11,100,101,110,111,---
この第100項はこれを2進法と考えれば
100=26+25+22より 110010
3進法の110010は10進法では
36+35+32=981
ということで 答は981
解答・その16
(ペンネ−ム:ヒャクレン・ラランジャ)
答 981
考え方
100を2進法であらわすと、1100100になります。
3進法の1100100は、10進法に直すと、
36(729)+35(243)+32(9)=981となります。
解答・その17
(ペンネ−ム:スモークマン)
1,10,11,・・・3進法
これの100番目ということは、2進法で100を表す、
100=64+32+4=26+25+22=1100100
を3進法に戻せば、
36+35+32=729+243+9=981
解答・その18
(ペンネ−ム:Nと〜)
この数列に現れる数を三進法で表すと、各桁は1か0。1以上で考える
という条件を忘れずに考えると……。
100を二進法で表すと(100=64+32+4なので)1100100。
これをそのまま三進法に読み直すと、36+35+32=729+243+9=981。
解答・その19
(ペンネ−ム:夜ふかしのつらいおじさん)
この問題は二進法と三進法を組合わせて考えると解けます。
3nの形をした整数の和を考えることは、数を三進法で考えるということです。
相異なる整数ということは、三進法で数を表したとき、どの位にも数字の「2」が現れないということです。
つまり、数字の「0」と「1」だけを用いて三進法で数を考えるということです。
解答は、百を二進法で表して、それを三進法の数と考えて値を調べればよいわけです。
まず、百は二進法で「1100100」となります。
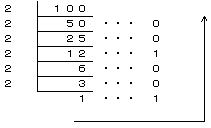
次に、「1100100」という数を三進法の数と考えると
36+35+32=981
正解者
| のっこん | nao | 夜ふかしのつらいおじさん |
| T_Tatekawa | Toru | オヤジ |
| teki | スモークマン | ヒャクレン・ラランジャ |
| 転位反応 | 杖のおじさん | バルタン星人 |
| テレスとアリス | 巷の夢 | 三角定規 |
| こまったコ | kohji | Nと〜 |
| まーや |
まとめ
この数列を構成する数は、
a0・1+a1・3+a2・32+a3・33+・・・
(ただし、ai=0,1)
と表すことができますので、多くの方の解答にあるように、
2進法と3進法を組み合わせて考えることができます。
つまり、100を2進法表記し、それによってaiが決まり、
そのaiを上記の式に当てはめれば、求める数になるわけですね。
 top
top