１２９．展開図の問題
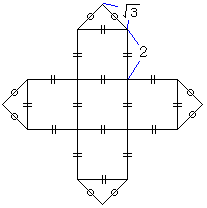
右の図のような、正方形と二等辺三角形からなる展開図を組み立ててできるへこみのない 立体の体積を求めなさい。ただし、正方形の１辺の長さは２、二等辺三角形の等しい２辺の
長さは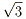
とする。
問題の出典
広中杯ハイレベル中学数学に挑戦
算数オリンピック委員会監修
講談社ブルーバックス
2003年トライアル問題
答えと解説
解答・その1
（ペンネ−ム：オヤジ）
求める体積は、
（一辺２の立方体の体積）＋（底面積４・高さ１の四角錐の体積）
＝ ８＋（１／３）・４・１
＝ ８＋＋４／３＝２８／３
∴ ２８／３
解答・その2
（ペンネ−ム：のっこん）
立体の体積は、正六面体の体積と四角すいの体積の合算で求められる
正六面体の体積は 2*2*2=8
四角すいの体積は
底面積が 2*2=4
高さが 1 だから（説明が必要だろうか？）
1/3*4*1=4/3
よって立体の体積は 8+4/3=28/3
解答・その3
（ペンネ−ム：転位反応）
立体の体積は、立方体と正四角錘の体積の和に等しい。
さて、正四角錘の高さは二等辺三角形の等しい２辺の長さと
正方形の対角線から１と求められ、立方体の高さの１／２に
等しい。よって、正四角錘を６個集めると、立方体の体積に
等しいことになる。
従って、求める立体の体積は、
２×２×２×（１＋１／６）＝２８／３
解答・その4
（ペンネ−ム：テレスとアリス）
展開図を組み立ててできる立体は、立方体と四角錐でできた立体と考えます。
立方体は一辺が２なので、体積は、
２×２×２＝８
です。四角錐は、底面は一辺が２の正方形です。
四角錐の高さは、二等辺三角形の一辺と底面の対角線の半分とで出来る直角三角形により、
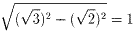
です。四角錐の体積は、
（２×２×１）÷３＝４/３
です。よって、立体の体積は、
８+４/３＝２８/３
となります。
解答・その5
（ペンネ−ム：杖のおじさん）
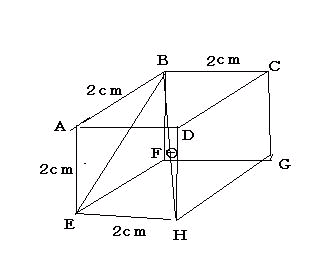
答え ２８／３cm3です。
線E，Bは面 Ａ，Ｂ，Ｅ，Ｆの対角線です。線B，Hは辺２ｃｍの立方体の対角線でその線分の中点をＯとします。
E，Bを求めます。２2＋２2＝Ｘ2→８＝Ｘ2→Ｘ＝２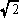
B，Hを求めます。２2（２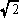）2＝Ｙ2→１２＝Ｙ2→Ｙ＝２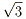
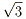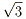線分Ｏ，Hは２÷２＝です。
従って２ｃｍの立方体の屋根の部分E，F，G，H，Ｏは辺２ｃｍの立方体の６分の１の体積である事が分かります。
従って求める全体の体積は式は次の通りです。
立方体の体積＝２3＋（２3）÷６＝（８×６＋８）÷６
（５６÷６）＝２８÷３cm3です。
解答・その6
（ペンネ−ム：ヒャクレン・ラランジャ）
答え 28/3
考え方
この展開図を組み立ててできる立体は、一辺２の立方体と底面の一辺が２で
の辺がルート３の正四角すいを組み合わせたものである。
立方体の体積
２×２×２＝８
正四角すいの体積
高さは１になるので、
２×２×１÷３＝4/3
よって、全体の体積は、
８＋4/3＝28/3 になる。
解答・その7
（ペンネ−ム：こまったコ）
とりあえず立方体の部分の体積を求めると
2 x 2 x 2 =8
残りの上の四角錘の部分の体積を求めるためにまず四角錘の高さを求める。
まず、四角錘の周りの二等辺三角形の高さaを求める。
二等辺三角形の等しい2辺の長さは 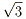なので
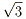()2 = 12 + a2
よって a=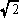
等しい2辺の長さをaとし、残りの辺の長さが2である二等辺三角形の高さbは
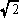()2 = 12 + b2 よって b= 1
よって四角錘の高さは1 四角錘の体積は
2 x 2 x 1 ÷ 3 = 4/3
よってこの立体の体積は
8 + 4/3 = 8.75
解答・その8
（ペンネ−ム：迷子の雄猫）
出来上がる立体は、一辺が２の立方体と、底面が(一辺が２の正方形)である４角錐に分
割できる。
当該四角錐の高さをh、底面の対角線の長さを2sとおく。
三平方の定理より、
(2s)2 = 22 + 22
よってs = 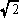三平方の定理より、
h2 + s2 = (当該四角錐の斜辺の長さ)2 = 3
よってh = 1
四角錐の体積は(底面積) * (高さ) / 3 より 4 / 3
よって出来上がる立体の体積は、
(2 * 2 * 2) + (4 / 3) = 9 + 1 / 3
答：９と３分の１
解答・その9
（ペンネ−ム：バルタン星人）
解答：２８／３
解法：立方体と四角錐の体積の和
四角錐は頂点から辺に降ろした垂線の長さが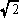
｛＝
｝
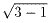正方形の中心までの長さは１なので高さも１｛＝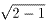
｝
四角錐の体積は１／３×２×２×１＝４／３
立方体体積８を加え２８／３
解答・その10
（ペンネ−ム：teki）
答え ９＋１／３ ｃｍ３
１辺２ｃｍの立方体に四角錐がくっついた形ですね。
問題は四角錐の高さですが、斜辺、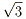
直角を挟む１辺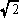の直角三角形のもう１つの辺の長さになりますね。
で、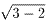
＝１ｃｍです。
後は、２×２×２＋２×２×１×１÷３＝８＋４／３＝９＋１／３ ですよね。
ちょっとした空間把握能力があれば、暗算で出てきます。
解答・その11
（ペンネ−ム：三角定規）
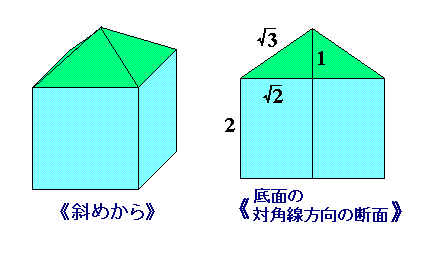
《解》
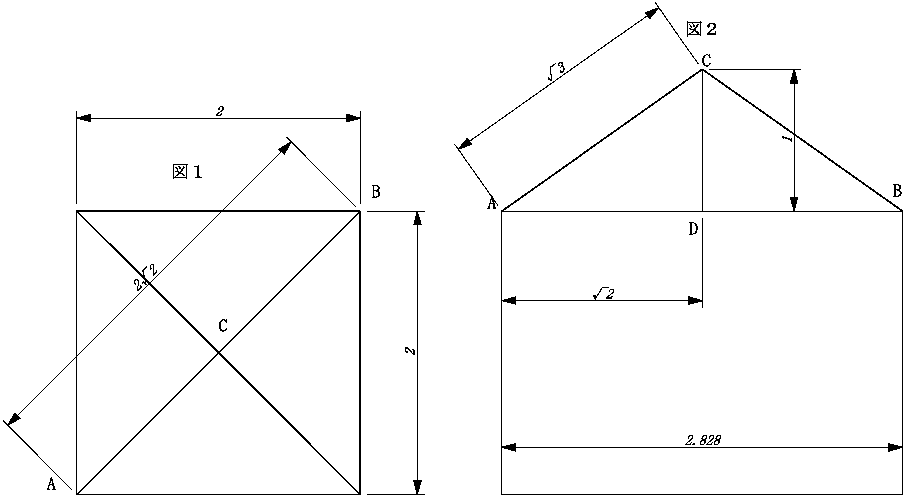
展開図を組み立てると，図左のような寄棟家屋ができあがります。
図右のように，屋根の部分の高さは １ になるから，体積は，
２×２×２＋(１/３)×２×２×１＝２８/３ …［答］
解答・その12
（ペンネ−ム：解答ルパン）
展開図からできる立体は一辺が２の立方体と底面が２の正方形をもつ四角すいで成って
いるので
立方体の体積は２３＝８
四角すいの高さは、そのの頂点から底面に下ろした垂線が底面の二つの対角線の交点と
交わるため、四角すいの高さは
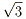斜辺が、
底辺が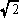となる直角三角形の残りの辺となるため、
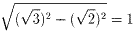
となるから、四角柱の体積は
２２×１／３＝４／３
よって、求める立体の体積は
８＋４／３＝２８／３
となります。
解答・その13
（ペンネ−ム：nao）
問題は１辺２の立方体と、底面の１辺が２の正方形で稜線が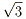の四角錐にわけられ
ます。
１辺２の立方体は２×２×２＝８、底面の１辺が２の正方形で稜線が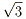の四角錐の
高さは１なので２×２×１×（１／３）＝４／３。
よって８＋（４／３）＝２８／３・・・答え
解答・その14
（ペンネ−ム：信三）
答え： 28/3
過程：ピラミッドを真上から見て出来る直角二等辺三角形は、
斜辺の長さが２なので、直角をはさむ辺の長さは「２の平方根」
となる。この辺に垂直の方向からピラミッドを見ると、
斜辺が「３の平方根」の直角三角形で、直角をはさむ２辺のうち、
１辺の長さが「２の平方根」なので、ピラミッドの高さに当たる残る１辺は、
三平方の定理で「１」となる。
このピラミッドは内側に押し込むと土台の立方体の体積の６分の１を
占める物だから、全体の体積は 8X7/6=28/3 となる。
解答・その15
（ペンネ−ム：スモークマン）
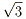(）2=12+(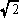)2だから、
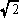()2=12+12 となり、
高さ1の四角錐だから、2x2x1x1/3=4/3
下の立方体は、2x2x2=23
合わせて、8+4/3=28/3 cm3
解答・その16
（ペンネ−ム：やなせ）
この展開図を組み立てると条件から各辺２ｃｍの立方体の上に
四角錐がのっかてるって事になりますよね。
立方体の体積は
２×２×２＝８
さて四角錐の体積ですけど高さが解れば四角柱の１／３ってことだから
問題は高さがいくらかって事ね
図参照でお願いします。
面倒お掛けしますね。
錐の上から見るとこうなります（図１）
対角ＡとＢの断面を横から見るとこんな具合かな（図２）
頂点ＣＡの長さは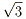
ＡＤの長さは
立方体各辺の長さが２なので対角線ＡＢは２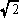になり
ＡＤはその半分だから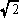です。
四角錐の高さＣＤは直角三角形の定理？から
×
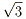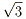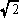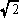−×＝１
さて高さが出ましたので四角錐の体積は
２×２×１÷３＝４／３
やれやれやっと出来ました。そうです答えは４／３でっす・・・なぁんて
何時もこんな具合に間違うんですよね
最後の答えです（笑）
８＋４／３＝９．３３３ｃｍ3
解答・その17
（ペンネ−ム：Toru）
一辺２の立方体 と 底面が一辺２の正方形で高さが１の四角錐の和ですよね。
23+2x2x1x1/3=28/3 答え 28/3
解答・その18
（ペンネ−ム：浦島五郎）
展開図を組み立てたら、正立方体の上に四角錐が乗った家型になる。
（問題のへこみのない立方体という条件で凸型に）
四角錐の高さは、斜辺は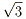で、
底辺の角から頂点から降ろした
中心までが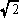だから
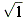です。 すると体積は、次のようになります。
２×２×２（正立方体部分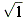）+ ×２×２／３（四角錐部分）＝２８／３
どうして四角錐が１／３で求められるのかは？？？ですが。(*^_^*)
解答・その19
（ペンネ−ム：kohji）
1辺の長さが2の立方体の体対角線の長さは2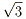なので、
展開図の二等辺三角形を側面とする四角錐は
1辺の長さが2の立方体の6分の1の体積になる。
よって求める体積は
23(1+1/6)=28/3
解答・その20
（ペンネ−ム：まーや）
（答え）28/３
組み立ててできる立体は、１辺２の立方体の上に四角錐が乗った形である。
立方体の体積は
２×２×２＝８・・・（ア）
四角錐の高さをhとすると、
三平方の定理より
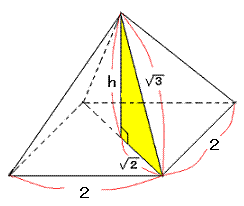
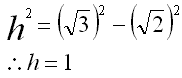
四角錐の体積は
２×２×１÷３＝４/３・・・（イ）
（ア）、（イ）より立体の体積は
８＋４/３＝28/３・・・（答え）
解答・その21
（ペンネ−ム：巷の夢）
題意より、一辺の長さが2の立方体とその立方体の1/6の四角錐を加えたものが求めるものである。
因って、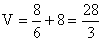
となる。
何故なら、立方体の点対称角の離れは 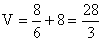より であり、
この長さの半分が四角錐の斜辺の長さになっていることから分かる。
解答・その22
（ペンネ−ム：STRAIGHTBOURBON）
1)まず、立方体の上に飛び出る4角錐の側面の3角形の高さを求めます。
高さをhとすると、ピタゴラスの定理から、
h2 = (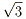)2 - 12= 3-1 = 2
h =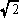
2)4角錐の高さをHとすると、
H2 = h2 - 12 = 2-1 = 1
H = 1
3)Hが立方体の高さの半分なので、
この立体を6個、頭をつき合わせるように組みたてると、ぴったりかみ合って
3次元十字のかたち(上下左右どちらから見ても十字に見えるかたち)
になる。
4)できあがった3次元十字は立方体7つで出来上がっている。
そこで求める立体の体積Vは以下のように求められる。
V = 23 * 7 / 6 = 28/3 = 9 + 1/3
今回の問題を解いて思いついたことがあります。
出題で「組み立ててできるへこみのない立体」
という条件がありますが、逆に
「組み立ててできるへこみのある立体」を
上記の解法のように6個組み合わせると、
3次元十字の中央にできる空洞の大きさは
ちょうど8になるので、立方体1個をまるまる隠せるのでは？
頭の中でその空間の形を思い描こうとしても、
うまくまとまりませんが...
以上、感想でした。
解答・その23
（ペンネ−ム：夜ふかしのつらいおじさん）
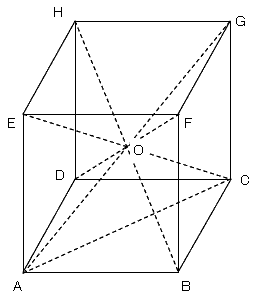
一辺の長さが２の立方体に対角線を引きます。（AG，BH，CE，DF）
底面の正方形に対角線を引きます。（AC)
三平方の定理より
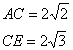
立方体の対角線は交点で二等分されます。
すると、四角錐OABCDは展開図を組み立てたとき、
立方体の上部にはみ出る四角錐と合同です。
立方体の内部にはこの四角錐が６個あり上部にはみ出たものをあわせると、
７個分の体積を求めればよいことになります。だから、体積Vは
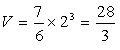
正解者
| teki | バルタン星人 | のっこん |
| ヒャクレン・ラランジャ | 杖のおじさん | 転位反応 |
| nao | STRAIGHTBOURBON | 信三 |
| スモークマン | やなせ | 夜ふかしのつらいおじさん |
| 巷の夢 | Toru | こまったコ |
| テレスとアリス | 解答ルパン | 三角定規 |
| 浦島五郎 | オヤジ | 迷子の雄猫 |
| kohji | まーや |
まとめ
できあがった立体は、立法体の上に四角錐がのっかった、家のような形になりますね。
何人かの方のご指摘にあるように、屋根の四角錐の部分が、ちょうど立方体の１／６になっています。
ところで、浦島五郎さんからのご質問に、四角錐の体積を求める時に、
どうして１／３をかけるのかというものがあります。底面の形に関係なく、
○○錘と呼ばれるものの体積は、○○柱を呼ばれるものの体積の１／３になります。
たとえば、円柱と円錐で考えると、
円柱の体積＝(底面積)×(高さ)
ですが、これは直感的に納得できますが、
円錐の体積＝1/3×(底面積)×(高さ)
となり、この事実はよく知られていますが、ではなぜ、1/3なのかということですね。
私も小学生の頃に、円錐の器に水を入れ、３回で円柱を満たすという検証をした記憶があります。
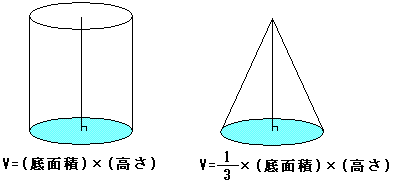
定積分を用いてみます。例えば、底面積Ｓ、高さｈの三角錐を、 この図のように、頂点が原点に、ｘ軸が底面に垂直になるように配置します。
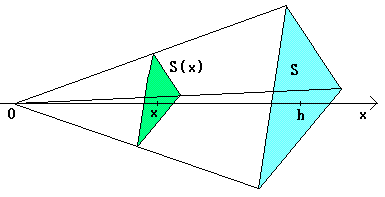
任意のｘで、ｘ軸に対して垂直に切り、その断面をＳ(x)とすると、
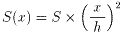
となります。なぜなら、元の三角錐と、切り口から左の小さい三角錐は相似となり、
その相似比は、ｘ：ｈとなります。面積比は、その２乗になり、
ｘ２：ｈ２となるからです。これをｘ＝０から、ｘ＝ｈまで定積分すれば、元の三角錐の体積となります。
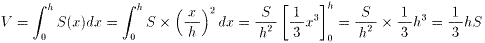
というわけで、体積 V=1/3×(底面積)×(高さ)となります。
底面の形に関係なく、この関係がなりたつこともわかると思います。
top