�P�Q�W�D�����`���琳���`��
�c�̒��������̒����������ł���悤�ȁA�����`�łȂ������`�̌`��������������B���̎��ɑ��āA����
�悤�ȑ�����J��Ԃ��B
�i����j
���̒����`�ɂӂ��܂��ő�̐����`��藎�Ƃ��B
�����̎��������`�ł���A����𑱂��A�����̎��������`�ł���A�����ő�����I���B
���삪�I���܂ł̉��A���̒����`�́u�ϐ��v�A�Ō�Ɏc���������`�̂P�ӂ̒������A����
�����`�́u��{�T�C�Y�v�Ƃ������Ƃɂ���B
�Ⴆ�A�Q�~�T�̒����`�́A�}�̂悤�ɑ��삪�J��Ԃ����̂ŁA�ϐ��R�A��{�T�C�Y�P�ƂȂ�B

(1) �P�S�S�~�Q�R�R�̒����`�̑ϐ��A��{�T�C�Y�����߂�B
(2) �Z�����̕ӂ̒����������A�������̕ӂ̒������V�Q�O�ł��钷���`�ŁA�ϐ����U�ł���悤�Ȃ��̂͂������邩�B
(3) �Z�����̕ӂ̒����������A�������̕ӂ̒������W�O�O�ł��钷���`�ŁA��{�T�C�Y���Q�ł���悤�Ȃ��̂͂������邩�B
(4) (�R�Q�P�|�P)�~(�R�P�W�|�P)�̒����`�̊�{�T�C�Y�����߂�B
���̏o�T
�L���t�n�C���x�����w���w�ɒ���
�Z���I�����s�b�N�ψ���ďC
�u�k�Ѓu���[�o�b�N�X
2005�N�t�@�C�i�����
�����Ɖ��
�E����1
�i�y���l�|���F�X���[�N�}���j
(1)
233-144=89
144-89=55
89-55=34
55-34=21
34-21=13
21-13=8
13-8=5
8-5=3
5-3=2
3-2=1
2-1=1
����āA�ϐ���11�A��{�T�C�Y��1
�E����2
�i�y���l�|���F�e���X�ƃA���X�j
(1)
����1�@�藎�Ƃ������`�̈�Ӂ�144�@���@�c��̒����`�̏c�Ɖ��̒�����144�~89
����2�@�藎�Ƃ������`�̈�Ӂ�89�@���@�c��̒����`�̏c�Ɖ��̒�����55�~89
����3�@�藎�Ƃ������`�̈�Ӂ�55�@���@�c��̒����`�̏c�Ɖ��̒�����55�~34
����4�@�藎�Ƃ������`�̈�Ӂ�34�@���@�c��̒����`�̏c�Ɖ��̒�����21�~34
����5�@�藎�Ƃ������`�̈�Ӂ�21�@���@�c��̒����`�̏c�Ɖ��̒�����21�~13
����6�@�藎�Ƃ������`�̈�Ӂ�13�@���@�c��̒����`�̏c�Ɖ��̒�����8�~13
����7�@�藎�Ƃ������`�̈�Ӂ�8�@���@�c��̒����`�̏c�Ɖ��̒�����8�~5
����8�@�藎�Ƃ������`�̈�Ӂ�5�@���@�c��̒����`�̏c�Ɖ��̒�����3�~5
����9�@�藎�Ƃ������`�̈�Ӂ�3�@���@�c��̒����`�̏c�Ɖ��̒�����3�~2
����10�@�藎�Ƃ������`�̈�Ӂ�2�@���@�c��̒����`�̏c�Ɖ��̒�����1�~2
����11�@�藎�Ƃ������`�̈�Ӂ�1�@���@�c��̒����`�̏c�Ɖ��̒�����1�~1
����āA�ϐ���11�A��{�T�C�Y��1�B
�E����3
�i�y���l�|���F���܂����R�j
(1) �������̕ӂ̒�������Z�����̕ӂ̒�����������邩�𐔂���悢�B
�@233��144=1 �]��@89
�@144��89=1 �]��@55
�@89��55=1�@�]��@34
�@55��34=1 �]��@21
�@34��21=1�@�]��@13
�@21��13=1�@�]��@8
�@13��8=1�@�]��@5
�@8��5=1�@�]��@3
�@5��3=1�@�]��@2
�@3��2=1�@�]��@1
�@2��1=2�@...���̂����Е����Ō�Ɏc�鐳���`�B
1+1+1+1+1+1+1+1+1+1+2-1=11
����đϐ�11�A��{�T�C�Y1�B
(4)
�R21-1= 10460353202
�R18-1= 387420488
10460353202��387420488=27 �]�� 26
387420488��26=14900788
��{�T�C�Y��26�B
�E����4
�i�y���l�|���F���C�j
�Ȃ��Ȃ����܂��������@���v�����Ȃ������̂Ŗ������
�R���s���[�^�[�Ɍv�Z�������܂����B
�v���O�����̓G�N�Z���̃}�N���ł��B�A���S���Y����
���[�N���b�h�̌ݏ��@�Ɏ������@���g���Ă���܂��B
(1)��{�T�C�Y �P�A�ϐ� �P�P
(2) �@8��
�ȉ��ڍ�
192�A200�A280�A315�A405�A440�A520�A528
(3) 160��
(4)��{�T�C�Y �Q�U�A���Ȃ݂ɑϐ��� 14900814
�Q�l�܂łɁA�ȉ��v���O�����̏ڍׂł��B
Sub BoxCal()
Dim xx As Currency
Dim yy As Currency
Dim taisu As Long
Dim Tcounter As Integer
Dim IsThisTSix As Integer
taisu = 0
IsThisTSix = 1
Tcounter = 1
xx = 720
yy = 0
While IsThisTSix < 720
yy = IsThisTSix
While xx > 0 And yy > 0
If xx = yy Then
GoTo NEXTNUMBER:
Else
If xx > yy Then
xx = xx - yy
taisu = taisu + 1
Else
If yy > xx Then
yy = yy - xx
taisu = taisu + 1
End If
End If
End If
Wend
NEXTNUMBER:
If taisu = 6 Then
Range("B" & Tcounter).Value = IsThisTSix
Tcounter = Tcounter + 1
End If
IsThisTSix = IsThisTSix + 1
taisu = 0
xx = 720
Wend
Excel.Workbooks("BOX.xls").Worksheets("Sheet1").Select
With Selection
Range("A1").Value = Tcounter - 1
End With
End Sub
Sub Kakunin()
Dim xx As Currency
Dim yy As Currency
Dim taisu As Long
xx = (3 ^ 21 - 1)
yy = (3 ^ 18 - 1)
taisu = 0
While xx > 0 And yy > 0
If xx = yy Then
GoTo NEXTNUMBER:
Else
If xx > yy Then
xx = xx - yy
taisu = taisu + 1
Else
If yy > xx Then
yy = yy - xx
taisu = taisu + 1
End If
End If
End If
Wend
NEXTNUMBER:
Excel.Workbooks("BOX.xls").Worksheets("Sheet1").Select
With Selection
Range("A1").Value = taisu
Range("A2").Value = xx
Range("A3").Value = yy
End With
End Sub
Sub Happyaku()
Dim xx As Currency
Dim yy As Currency
Dim taisu As Long
Dim counter As Integer
Dim IsTheGCDTwo As Integer
IsTheGCDTwo = 2
counter = 1
While IsTheGCDTwo < 800
yy = IsTheGCDTwo
xx = 800
While xx > 0 And yy > 0
If xx = yy Then
GoTo NEXTNUMBER:
Else
If xx > yy Then
xx = xx - yy
taisu = taisu + 1
Else
If yy > xx Then
yy = yy - xx
taisu = taisu + 1
End If
End If
End If
Wend
NEXTNUMBER:
If yy = 2 Then
Excel.Workbooks("BOX.xls").Worksheets("Sheet1").Select
With Selection
Range("B" & counter).Value = IsTheGCDTwo
End With
counter = counter + 1
End If
IsTheGCDTwo = IsTheGCDTwo + 1
Wend
Excel.Workbooks("BOX.xls").Worksheets("Sheet1").Select
With Selection
Range("A1").Value = counter - 1
End With
End Sub
�E����5
�i�y���l�|���F�]�ʔ����j
(1)�@�����`�̒������̕ӂ̒�����Z�����̕ӂ̒����Ŋ����āA��o���鐳���`�̌����J�E���g����B
�@�@�m�����`�̒������̕ӂ̒����n���m�����`�̌��n�~�m�Z�����̕ӂ̒����n�{�m�]�����ӂ̒����n
�̌v�Z���Ő�������ƈȉ��̒ʂ�B
| �v�Z�� | ��o���������`�̌��̗v |
|---|---|
| 233��1�~144�{89 | 1 |
| 144��1�~89�{55 | 2 |
| 89��1�~55�{34 | 3 |
| 55��1�~34�{21 | 4 |
| 34��1�~21�{13 | 5 |
| 21��1�~13�{8 | 6 |
| 13��1�~8�{5 | 7 |
| 8��1�~5�{3 | 8 |
| 5��1�~3�{2 | 9 |
| 3��1�~2�{1 | 10 |
| 2��2�~1 | 12 |
����āA���̒����`�̑ϐ��͂P�P�A��{�T�C�Y�͂P
���̕��@�́A���[�N���b�h�̌ݏ��@�ɂ��ő�������߂邱�Ƃɓ������B
(2)�@�����`�̑ϐ����U�ł��邱�Ƃ́A�V�̐����`����\������Ă��邱�Ƃ��Ӗ����A
���̂����ŏ��̐����`�̕ӂ̒����́A�����`�̏c�Ɖ��̕ӂ̒����̍ő���ɓ������B
�����ŁA720=24�~32�~5�Ȃ̂ŁA�ő���̌��͈ȉ��̒ʂ�B
1,2,3,4,5,6,8,9,12,15,16,18,20,24,30,36,40,45,48,60,72,80,90,120,144,180,240,360
���āA��{�T�C�Y���̐����`�Q����o�����āA��ɂ��傫�Ȑ����`���ł���悤�ɑS���łV��
�����`��g������Ɖ��L�̒����`���쐬�ł���B���̒����`�͖ʐύő�Œ������̕ӂ̒������ő�ł���B
���̕ӂ̒����͂Q�P���Ȃ̂ŁA�Q�P�����V�Q�O�Ƃ��Ă����R�S�B����āA�R�U�ȏ�̍ő�����l����Ηǂ��B
����ɁA80,120,240,360��40�̔{���A90,180��45�̔{���A144��72�̔{���Ȃ̂ŁA���ǂ̂Ƃ���A
36,40,45,48,60,72�̔{����Z�����̕ӂ̒����Ƃ��āA�ϐ���������悢�B

�Ⴆ�A
720=3�~200�{120
200=1�~120�{80
120=1�~80�{40
80=2�~40
�ϐ���3+1+1+2-1=6
���،��ʂ́A���L�̒ʂ�W�ʂ�
36�̔{���F�Y������
40�̔{���F200,280,440,520
45�̔{���F315,405
48�̔{���F192,528
60�̔{���F�Y������
72�̔{���F�Y������
(3)�@��{�T�C�Y��2�Ƃ������Ƃ́A�ő����2�Ƃ������Ƃł���B
800=25�~52�Ȃ̂ŁA
2�̔{������4�y��10�̔{���������Β����`�̒Z�����̕ӂ̒��������߂���
2�`100��20�ʂ肠��̂ŁA2�`798�܂ł�160�ʂ�

(4)�@321-1=33�i318-1�j+33-1
318-1=(315+312+39+36+33+1)�i33-1�j
�ő����33-1�A����Ċ�{�T�C�Y��33-1=26
�E����6
�i�y���l�|���Fnao�j
(1)
�@�@�Q�R�R���P�S�S���P�E�E�E�W�X
�@�@�P�S�S���W�X���P�E�E�E�T�T
�@�@�W�X���T�T���P�E�E�E�R�S
�@�@�T�T���R�S���P�E�E�E�Q�P
�@�@�R�S���Q�P���P�E�E�E�P�R
�@�@�Q�P���P�R���P�E�E�E�W
�@�@�P�R���W���P�E�E�E�T
�@�@�W���T���P�E�E�E�R
�@�@�T���R���P�E�E�E�Q
�@�@�R���Q���P�E�E�E�P
�@�@�Q���P���Q�E�E�E�O
�����@�ϐ��P�P�@��{�T�C�Y�P
(2)
�ϐ����U�Ƃ������Ƃ́A�����`�V�ɐ蕪������悢�B
��ԏ����������`�̃T�C�Y���i�P�j�Ƃ��āA�i�P�j�~�Q�A�i�Q�j�~�R�A�i�V�j�~�Q��
�蕪����ƒ������̕ӂ̒������i�P�U�j�ɂȂ��ĂV�Q�O��������B
���̏ꍇ
�i�V�Q�O�A�R�P�T�j�̒����`���ł��A��{�T�C�Y�͂S�T�ɂȂ�B
���l�ɂ��āA�i�P�j
�~�Q�A�i�Q�j�~�R�A�i�V�j�~�P�A�i�X�j�~�P�ɐ蕪���Ă��������̕ӂ́i�P�U�j��
�Ȃ�A��͂��{�T�C�Y�S�T�ŁA�i�V�Q�O�A�S�O�T�j�̒����`���ł���B
���l�ɂ��āA���ׂ����ʂ��܂Ƃ߂�ƁA
��{�T�C�Y�S�O�̂���
�i�V�Q�O�A�Q�W�O�j�F�i�P�j�~�R�A�i�R�j�~�P�A�i�S�j�~�P�A�i�V�j�~�Q
�i�V�Q�O�A�S�S�O�j�F�i�P�j�~�R�A�i�R�j�~�P�A�i�S�j�~�P�A�i�V�j�~�P�A�i�X�j�~�P
�i�V�Q�O�A�Q�O�O�j�F�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�P�A�i�T�j�~�R
�i�V�Q�O�A�T�Q�O�j�F�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�P�A�i�T�j�~�Q�A�i�P�R�j�~�P
��{�T�C�Y�S�T�̂���
�i�V�Q�O�A�R�P�T�j�F�i�P�j�~�Q�A�i�Q�j�~�R�A�i�V�j�~�Q
�i�V�Q�O�A�S�O�T�j�F�i�P�j�~�Q�A�i�Q�j�~�R�A�i�V�j�~�P�A�i�X�j�~�P
��{�T�C�Y�S�W�̂���
�i�V�Q�O�A�P�X�Q�j�F�i�P�j�~�R�A�i�R�j�~�P�A�i�S�j�~�R
�i�V�Q�O�A�T�Q�W�j�F�i�P�j�~�R�A�i�R�j�~�P�A�i�S�j�~�Q�A�i�P�P�j�~�P
����ȊO�ɂȂ��Ƃ������Ƃ������邽�߂ɁA���ׂẲ\���������Ă݂܂����B
�i�P�j�~�V�̂����@�������̕Ӂi�V�j�Z�����̕Ӂi�P�j
�i�P�j�~�U�A�i�U�j�~�P�̂����@�i�V�j�Ɓi�U�j
�i�P�j�~�T�A�i�T�j�~�Q�̂����@�i�P�P�j�Ɓi�T�j
�i�P�j�~�T�A�i�T�j�~�P�A�i�U�j�~�P�̂����@�i�P�P�j�Ɓi�U�j
�i�P�j�~�S�A�i�S�j�~�R�̂����@�i�P�R�j�Ɓi�S�j
�i�P�j�~�S�A�i�S�j�~�Q�A�i�X�j�~�P�̂����@�i�P�R�j�Ɓi�X�j
�i�P�j�~�S�A�i�S�j�~�P�A�i�T�j�~�Q�̂����@�i�P�S�j�Ɓi�T�j
�i�P�j�~�S�A�i�S�j�~�P�A�i�T�j�~�P�A�i�X�j�~�P�̂����@�i�P�S�j�Ɓi�X�j
�i�P�j�~�R�A�i�R�j�~�S�̂����@�i�P�R�j�Ɓi�R�j
�i�P�j�~�R�A�i�R�j�~�R�A�i�P�O�j�~�P�̂����@�i�P�R�j�Ɓi�P�O�j
�i�P�j�~�R�A�i�R�j�~�Q�A�i�V�j�~�Q�̂����@�i�P�V�j�Ɓi�V�j
�i�P�j�~�R�A�i�R�j�~�Q�A�i�V�j�~�P�A�i�P�O�j�~�P�̂����@�i�P�V�j�Ɓi�P�O�j
�i�P�j�~�R�A�i�R�j�~�P�A�i�S�j�~�R�̂����@�i�P�T�j�Ɓi�S�j
�i�P�j�~�R�A�i�R�j�~�P�A�i�S�j�~�Q�A�i�T�P�j�~�P�̂����@�i�P�T�j�Ɓi�P�P�j
�i�P�j�~�R�A�i�R�j�~�P�A�i�S�j�~�P�A�i�V�j�~�Q�̂����@�i�P�W�j�Ɓi�V�j
�i�P�j�~�R�A�i�R�j�~�P�A�i�S�j�~�P�A�i�V�j�~�P�A�i�T�P�j�~�P�̂����@�i�P�W�j�Ɓi�P�P�j
�i�P�j�~�Q�A�i�Q�j�~�T�̂����@�i�P�P�j�Ɓi�Q�j
�i�P�j�~�Q�A�i�Q�j�~�S�A�i�X�j�~�P�̂����@�i�P�P�j�Ɓi�X�j
�i�P�j�~�Q�A�i�Q�j�~�R�A�i�V�j�~�Q�̂����@�i�P�U�j�Ɓi�V�j
�i�P�j�~�Q�A�i�Q�j�~�R�A�i�V�j�~�P�A�i�X�j�~�P�̂����@�i�P�U�j�Ɓi�X�j
�i�P�j�~�Q�A�i�Q�j�~�Q�A�i�T�j�~�R�̂����@�i�P�V�j�Ɓi�T�j
�i�P�j�~�Q�A�i�Q�j�~�Q�A�i�T�j�~�Q�A�i�T�Q�j�~�P�̂����@�i�P�V�j�Ɓi�P�Q�j
�i�P�j�~�Q�A�i�Q�j�~�Q�A�i�T�j�~�P�A�i�V�j�~�Q�̂����@�i�P�X�j�Ɓi�V�j
�i�P�j�~�Q�A�i�Q�j�~�Q�A�i�T�j�~�P�A�i�V�j�~�P�A�i�T�Q�j�~�P�̂����@�i�P�X�j�Ɓi�P�Q�j
�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�S�̂����@�i�P�S�j�Ɓi�R�j
�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�R�A�i�T�P�j�~�P�̂����@�i�P�S�j�Ɓi�P�P�j
�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�Q�A�i�W�j�~�Q�̂����@�i�P�X�j�Ɓi�W�j
�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�Q�A�i�W�j�~�P�A�i�T�P�j�~�P�̂����@�i�P�X�j�Ɓi�P�P�j
�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�P�A�i�T�j�~�R�̂����@�i�P�W�j�Ɓi�T�j
�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�P�A�i�T�j�~�Q�A�i�T�R�j�~�P�̂����@�i�P�W�j�Ɓi�P�R�j
�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�P�A�i�T�j�~�P�A�i�W�j�~�Q�̂����@�i�Q�P�j�Ɓi�W�j
�i�P�j�~�Q�A�i�Q�j�~�P�A�i�R�j�~�P�A�i�T�j�~�P�A�i�W�j�~�P�A�i�T�R�j�~�P�̂����@�i�Q�P�j�Ɓi�P�R�j
�S���łR�Q�̏ꍇ������܂����B����Œ������̕ӂ��V�Q�O������鐔�ɂȂ��Ă�
��̂͂W�̂��������Ȃ��Ƃ������Ǝv���܂��B
(3)
�i�P�j�i�Q�j�̖��ŕ�����悤�ɁA���̖��̓��[�N���b�h�̌ݏ��@�ɂ��ő��
�݂̂�������}�`�ł���킵�����̂ł���B
����ŁA�������̕ӂ̒������W�O�O�ł��钷���`�Ŋ�{�T�C�Y���Q�ɂȂ�Ƃ�������
�́A�W�O�O�ƍő�����Q�ɂȂ���̂Ƃ������Ƃł���B
�@�@�@�W�O�O���Q���S�O�O
�S�O�O�Ƒf�ɂȂ鐔�͂��Ƃ��P�B
�W�O�O�ƂP�~�Q���Q�͊�{�T�C�Y���Q�ɂȂ�B�܂��A���̂��͂R�B
�W�O�O�ƂR�~�Q���U���ő���܂��͊�{�T�C�Y�͂Q�ɂȂ�B
�S�O�O�̑f�����͂Q�ƂT�Ȃ̂ŁA
�@�@�@�S�O�O���Q���Q�O�O�@�S�O�O���T���W�O�@�S�O�O���P�O���S�O
�ŁA�Q�O�O�{�W�O�[�S�O���Q�S�O���Q�܂��͂T�Ŋ����鐔�B
�c��̂S�O�O�\�Q�S�O���P�U�O�͂S�O�O�Ƌ��ʂ̈����������Ȃ��B
�����P�U�O��
(4)
���������łȂɂ����܂����@�����邩�ƍl�������A���w�Z���x���̎��̗͂ł͂ƂĂ�
�y���A���ۂɊ��Z�����s��������̂��Ƃ�����������Ă݂���A���Ƃ��ł���
�悤�ȋC������B
�@�@�@(�R�Q�P�|�P)��(�R�P�W�|�P)���R�R�E�E�E�R�R�[�P
�@�@�@(�R�P�W�|�P)���i�R�R�[�P�j���R�P�T�{�R�P�Q�{�R�X�{�R�U�{�R�R�{�P�E�E�E�O
�������Q��Ŋ���ꂽ�B
�ϐ��͂ł��������`�̐������P�Ȃ̂łR�R�{�R�P�T�{�R�P�Q�{�R�X�{�R�U
�{�R�R�{�P�[�P���R�P�T�{�R�P�Q�{�R�X�{�R�U�{�R�R�~�Q
�܂���{�T�C�Y�͍Ō�Ɋ���������Ȃ̂łR�R�[�P���Q�U
�E����7
�i�y���l�|���Fkohji�j
(����`)
A*B(A>B)�̒����`�ɂ��āA
�@�@�@A=C*B+D�c(�A) A,B���m C={C|A>B*C�ƂȂ�ő�̎��R��}
�ƂȂ�悤��C,D���߂�B
(����`)�́A
�u(�A)��A*B�̒����`����B*B�̐����`��C�藎�Ƃ���B*D(B��D)�̒����`���c��B�v
�Ƃ������Ƃ��Ӗ�����B
�܂��ӂ�(����)�́A(����`)�Ő����Ďc���������`�ɂ����čX��(����`)���A������
�c�钷���`�������`�ɂȂ�܂ŌJ��Ԃ����Ƃł���B
�܂��AA*B�̒����`�̊�{�T�C�Y��(�A)�̎��̌`�ƃ��[�N���b�h�ݏ��@���A*B�̍ő���ƂȂ�B��
���đϐ��� {(�A)�̎���C�̘a} �ŗ^������B
(1)
(����`)���J��Ԃ��ƁA
�@�@�@233=1*144+89
�@�@�@144=1*89+55
�@�@�@89=1*55+34
�@�@�@55=1*34+21
�@�@�@34=1*21+13
�@�@�@21=1*13+8
�@�@�@13=1*8+5
�@�@�@8=1*5+3
�@�@�@5=1*3+2
�@�@�@3=1*2+1
�@�@�@2=1*1+1
����āA��{�T�C�Y 1�A�ϐ� 1*11=11
(2)
��ӂ�(����)�ɂ�����(����`)���J��Ԃ���m�Ƃ���B
�܂�n��ڂ�(����`)�̐���C�̒l��Cn�Ƃ���B
(i)m=1�̂Ƃ�
C1=6�Ȃ̂ŁA
720=6B+B �� B=720/7 ����͐����ł͂Ȃ��̂ŕs�K�B
(ii)m=2�̂Ƃ�
(C1,C2)=(1,5),(2,4),(3,3),(4,2),(5,1)
720=C1*B+D
B=C2*D+D�@�́@D=720/(C1*C2+C1+1)
B�������̂Ƃ�D�������ƂȂ邪�A
D=720/7,720/11,720/13,720/11 (����) �ƂȂ�̂ŕs�K�B
(iii)m=3�̂Ƃ�
(C1,C2,C3)=(1,1,4),(1,2,3),(1,3,2),(1,4,1),(2,1,3),(2,2,2),(2,3,1),(3,1,2)(3,2,1),(4,1,1)
720=C1*B+D
B=C2*D+E
D=C3*E+E�@�́@E=720/(C1*C2*C3+C1*C2+C1+1+C3)
��E=720/11,720/13,720/13,720/11,360/7,720/17,45,48,720/17,360/7 (����)
�ƂȂ�AB�������ł��邱�Ƃ�E�������ł��邱�Ƃ̕K�v�\�������ł��邱�Ƃ��l���āAE�������ɂ�
����̂�2�ʂ�Ȃ̂ŁAB��2�ʂ肠��B
(iv)m=4�̂Ƃ�
(C1,C2,C3,C4)=(1,1,1,3),(1,1,2,2),(1,1,3,1),(1,2,1,2),(1,2,2,1),(1,3,1,1),(2,1,1,2),(2,1,
2,1),(2,2,1,1),(3,1,1,1)
720=C1*B+D
B=C2*D+E
D=C3*E+F
E=C4*F+F�@�́@F=720/(C1*C2*C3*C4+C1*C2*C3+C1*C2+C1+1+C3+C1*C4+C3*C4)
��F=360/7,720/17,45,48,720/17,360/7,40,720/19,720/19,45 (����)
�ƂȂ�AB�������ł��邱�Ƃ�F�������ł��邱�Ƃ̕K�v�\�������ł��邱�Ƃ��l���āAF�������ɂ�
����̂�4�ʂ�Ȃ̂ŁAB��4�ʂ肠��B
(v)m=5�̂Ƃ�
(C1,C2,C3,C4,C5)=(1,1,1,1,2),(1,1,1,2,1),(1,1,2,1,1),(1,2,1,1,1),(2,1,1,1,1)
720=C1*B+D
B=C2*D+E
D=C3*E+F
E=C4*F+G
F=C5*G+G�@�́@G=720/(C1*C2*C3*C4*C5+C1*C2*C3*C4+C1*C2*C3+C1*C2+C1+1
+C1*C2*C5+C1*C4*C5+C3*C4*C5+C1*C4+C3*C4+C3+C5)
��F=40,720/19,720/19,40,240/7 (����)
�ƂȂ�AB�������ł��邱�Ƃ�G�������ł��邱�Ƃ̕K�v�\�������ł��邱�Ƃ��l���āAG�������ɂ�
����̂�2�ʂ�Ȃ̂ŁAB��2�ʂ肠��B
(vi)m=6�̂Ƃ�
(C1,C2,C3,C4,C5,C6)=(1,1,1,1,1,1) �Ȃ̂ŁA
720=B+D
B=1*D+E
D=1*E+F
E=1*F+G
F=1*G+H
G=1*H+H�@�́@H=720/21=240/7
B�������̂Ƃ�H�������ƂȂ�̂ŕs�K�B
(i)�`(vi)���A���߂���̂� 2+4+2=8�ʂ�
(3)
8800�ȉ��̎��R���ŁA800�Ƃ̍ő����2�ł�����̂̐������߂�悢�B
800-(���4�̔{����5�̔{��)
�@=800-{(�)+(4�̔{��)+(5�̔{��)-(���5�̔{��)-(4�̔{����5�̔{��)}
�@=800-{[800/2]+[800/4]+[800/5]-[800/5]/2-[800/20]}
�@=800-(400+200+160-80-40)
�@=160
(4)
321-1 �� 318-1 �̍ő�������߂�悢�B
�@�@�@321-1=318(33-1)+318-1
�@�@�@318-1=315(33-1)+315-1
�@�@�@315-1=312(33-1)+312-1
�@�@�@312-1=39(33-1)+39-1
�@�@�@39-1=36(33-1)+36-1
�@�@�@36-1=33(33-1)+33-1
�ȏ�̎��ƃ��[�N���b�h�ݏ��@����{�T�C�Y�� 33-1=26
�E����8
�i�y���l�|���F�O�p��K�j
�i�P�j
�i�Q�R�R�C�P�S�S�j���i�P�S�S�C�W�X�j���i�W�X�C�T�T�j���i�T�T�C�R�S�j���i�R�S�C�Q�P�j���i�Q�P�C�P�R�j���i�P�R�C�W�j��
�@���i�W�C�T�j���i�T�C�R�j���i�R�C�Q�j���i�Q�C�P�j���i�P�C�P�j
�ƂȂ邩��C�ϐ� �P�P�C��{�T�C�Y �P �c�m���n
�i�Q�j
�ǂ̂悤�Ɏ��𗧂Ă�����̂��킩��Ȃ��������߁C�G�N�Z�����l�ׂ������Ă݂܂����B���̌��ʁC
�@�@�i�V�Q�O�C�T�Q�W�j<��{�T�C�Y�S�W>�C�i�V�Q�O�C�T�Q�O�j<�S�O>�C�i�V�Q�O�C�S�S�O�j<�S�O>�C�i�V�Q�O�C�S�O�T�j<�S�T>
�@�@�i�V�Q�O�C�R�P�T�j<�S�T>�C�i�V�Q�O�C�Q�W�O�j<�S�O>�C�i�V�Q�O�C�Q�O�O�j<�S�O>�C�i�V�Q�O�C�P�X�Q�j<�S�W>�@�́@�W�� �c �m���n
�i�R�j
��{�T�C�Y�� �Q �Ƃ������Ƃ́C�W�O�O �� N �̍ő���� �Q �Ƃ������ƂŁC
�W�O�O���Q5�~�T2�@������C��ӂ��� N �̏����́C
�@�@�@(1)�@�f���� �Q ���P�������B
�@�@�@(2)�@�f���� �T �������Ȃ��B
���̂Q�̏������������́C
�P�`�S�O�O �܂ł̊�i�Q�O�O�j���� �T �̔{�������������́i�P�U�O�j�� �Q �{��������
�ŁC���̌��́C�P�U�O �c�m���n
�i�S�j
�@�@�@��18�|�P���i��3�|�P�j�i��15�{��12�{��9�{��6�{��3�{�P�j
�@�@�@��21�|�P���i��3�|�P�j�ix18�{��15�{��12�{��9�{��6�{��3�{�P�j
��15�{��12�{��9�{��6�{��3�{�P�@�Ɓ@x18�{��15�{��12�{��9�{��6�{��3�{�P�@�݂͌��ɑf������C
��18�|�P�@�Ƃ�21�|�P�@�̍ő���́C��3�|�P�B
�� �� �����R �Ƃ��C �R18�|�P�@�Ɓ@�R21�|�P�@�̍ő���́C�R3�|�P���Q�U�B
����āC �R18�|�P�@�Ɓ@�R21�|�P�@�̊�{�T�C�Y�́@�Q�U �c�m���n
�E����9
�i�y���l�|���F��ӂ����̂炢��������j
���̖��̓��[�N���b�h�̌ݏ��@�Ɠ������e�ł��B �ϐ��Ƃ́A�傫�����̐������������̐��Ŋ��邱�Ƃ��J��Ԃ��Ă������Ƃ��̏��̘a�ł��B ��{���Ƃ͍Ō�̗]��܂�Q�̐��̍ő���ł��B �Q���A�`�C�a�i�`���a�j�̍ő�����f�Ƃ��܂��B ����ƁA�`���`�f�f�A�a���a�f�f�ƕ\���܂��B �`���a�Ŋ������Ƃ��̏����p�A�]����q�Ƃ���ƁA �`���a�p�{�q �q���`�|�a�p �@���`�f�f�|�a�f�f�p �@���f(�`�f�|�a�f�p) �܂�]��͍ő���f�������Ɏ����܂��B ���ɂa���q(�a���q)�Ŋ���܂��B ���̗]�����Ɠ��l�̍l���łf�������Ɏ����Ƃ�������܂��B ���̂悤�Ȍv�Z���J��Ԃ��Ă����Ƃ��̂����Ɋ����܂��B ���̒��O�̗]�肪�f�ɂȂ�܂��B ���[�N���b�h�̌ݏ��@�̓����͂��Ƃ��Ƃ̐��̈�����m��Ȃ��Ă��ǂ����Ƃł��B
���̖��Œ����I�ɓ���������̂́i�S�j�ł��B
�@�@�@�R21�|�P���o(�R3)7�|�P�p��(�R3�|�P){(�R3)6�{(�R3)5�{(�R3)4�{(�R3)3�{(�R3)2�{(�R3)+�P}
�@�@�@�R18�|�P���o(�R3)6�|�P�p��(�R3�|�P){(�R3)5�{(�R3)4�{(�R3)3�{(�R3)2�{(�R3)+�P}
���A�R3�|�P���Q�U���Q���̌��ł��邱�Ƃ͕�����܂��B
�����R3�Ƃ�����
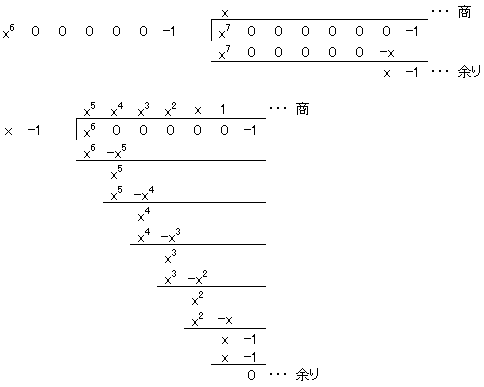
���Ax6-1��x7-1�̍ő���́Ax-1�ł��B
���ɉ�������̂́i�R�j�ł��B
�W�O�O��菬�����āA�W�O�O�Ƃ̍ő�����Q�ł��鐔�����߂�Ηǂ����ƂɂȂ�܂��B
�W�O�O���Q5�~�T2�Ȃ̂ŁA���̐��̂Q�ȊO�̈����͎��̂悤�ł��B
| 1 | 101 | 201 | 301 |
| 3 | 103 | 203 | 303 |
| 7 | 107 | 207 | 307 |
| 9 | 109 | 209 | 309 |
| 11 | 111 | 211 | 311 |
| 13 | 113 | 213 | 313 |
| 17 | 117 | 217 | 317 |
| 9 | 119 | 219 | 319 |
| 21 | 121 | 221 | 321 |
| 23 | 123 | 223 | 323 |
| 27 | 127 | 227 | 327 |
| 29 | 129 | 229 | 329 |
| 31 | 131 | 231 | 331 |
| 33 | 133 | 233 | 333 |
| 37 | 137 | 237 | 337 |
| 39 | 139 | 239 | 339 |
| 41 | 141 | 241 | 341 |
| 43 | 143 | 243 | 343 |
| 47 | 147 | 247 | 347 |
| 49 | 149 | 249 | 349 |
| 51 | 151 | 251 | 351 |
| 53 | 153 | 253 | 353 |
| 57 | 157 | 257 | 357 |
| 59 | 159 | 259 | 359 |
| 61 | 161 | 261 | 361 |
| 63 | 163 | 263 | 363 |
| 67 | 167 | 267 | 367 |
| 69 | 169 | 269 | 369 |
| 71 | 171 | 271 | 371 |
| 73 | 173 | 273 | 373 |
| 77 | 177 | 277 | 377 |
| 79 | 179 | 279 | 379 |
| 81 | 181 | 281 | 381 |
| 83 | 183 | 283 | 383 |
| 87 | 187 | 287 | 387 |
| 89 | 189 | 289 | 389 |
| 91 | 191 | 291 | 391 |
| 93 | 193 | 293 | 393 |
| 97 | 197 | 297 | 397 |
| 99 | 199 | 299 | 399 |
�\�̐��͂P����S�O�O�܂ł̐��ŋ����ƂT�̔{�������������̂ł��B
�ȏ� �P�U�O �ł��B
�i�P�j�͎��̂悤�ɉ����܂��B
�͂��߂ɂQ���̂����傫���������A�����������E�ɒu���܂��B
���Ɂu�傫�����Ə��������̍��v�Ɓu���������̐��v�ő傫���������A�����������E�ɒu���܂��B
�ȉ����̎葱�����J��Ԃ��Q���������ɂȂ�Ύ~�߂܂��B
| �X�e�b�v | �@ | �@ |
|---|---|---|
| 0 | 233 | 144 |
| 1 | 144 | 89 |
| 2 | 89 | 55 |
| 3 | 55 | 34 |
| 4 | 34 | 21 |
| 5 | 21 | 13 |
| 6 | 13 | 8 |
| 7 | 8 | 5 |
| 8 | 5 | 3 |
| 9 | 3 | 2 |
| 10 | 2 | 1 |
| 11 | 1 | 1 |
���ϐ��͂P�P�ł��B
�i�Q�j�͎��̂悤�ɉ����܂��B
��{���̐����`�ɉ������`���p�������Ă��������`�����܂��B
���߂͂ǂ�����n�߂Ă��ǂ��̂ʼnE�Ɍ��߂܂��B
�ȉ������`���p�����������͍��E�ɂ͖{���I�ȍ����Ȃ��̂ʼnE�Ƃ��܂��B
�ȉ������`���p�����������͏㉺�ɂ͖{���I�ȍ����Ȃ��̂ʼn��Ƃ��܂��B
���̂悤�ɉE���珉�߂āA�E�������ɐ����`���U��p���������Ƃ��l����ƈȉ��̌��ʂɂȂ�܂��B
�Q�ʂ�̔��f���T��̂ŁA�Q5���R�Q�ʂ�̏ꍇ������܂��B
���ۂ͋t�ɂ��ǂ��Ċ�{�`�ɖ߂�܂��B
�ł��������������`���A�������̕Ӂ~�Z�����̕ӂƂ��ĕ\���܂��B
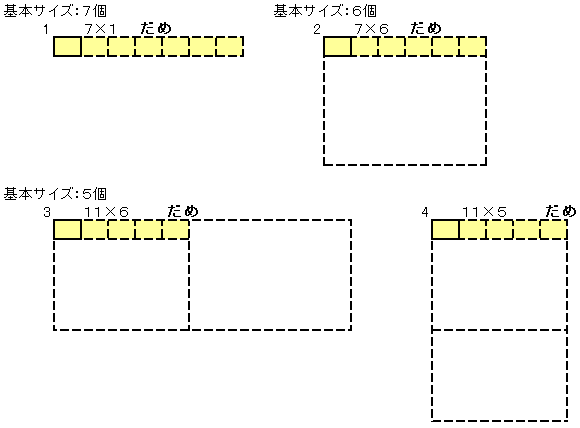
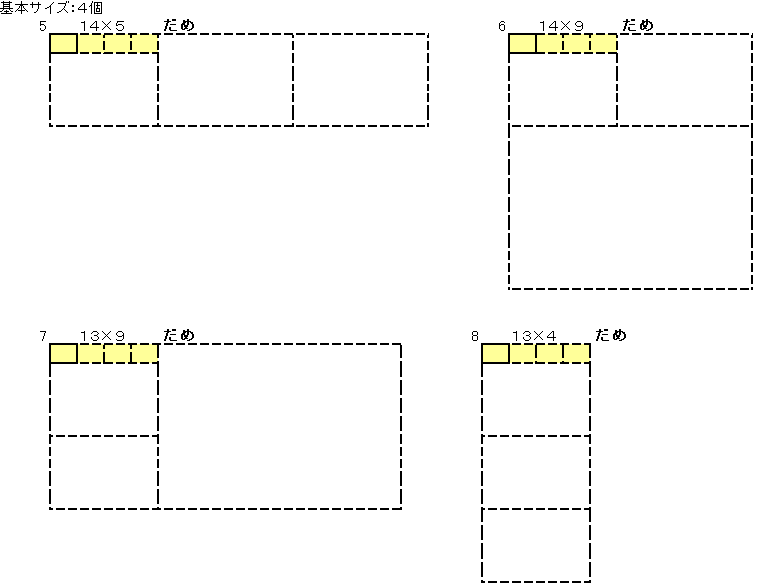
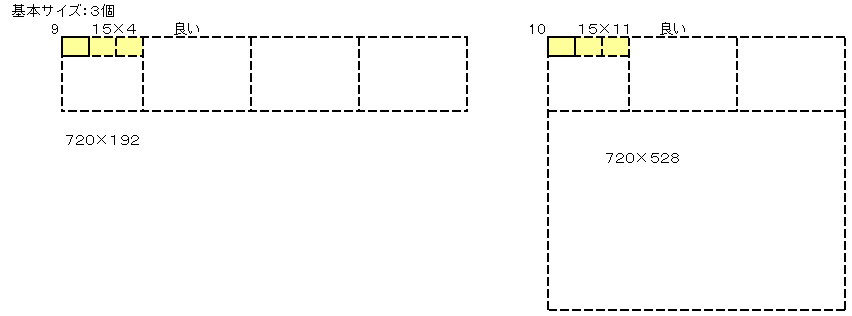
�V�Q�O���Q4�~�R2�~�T�Ȃ̂Œ������̕ӂ��V�Q�O�̖ɂȂ��Ă���Ηǂ����ƂɂȂ�܂��B
���̂悤�ɂW����܂��B
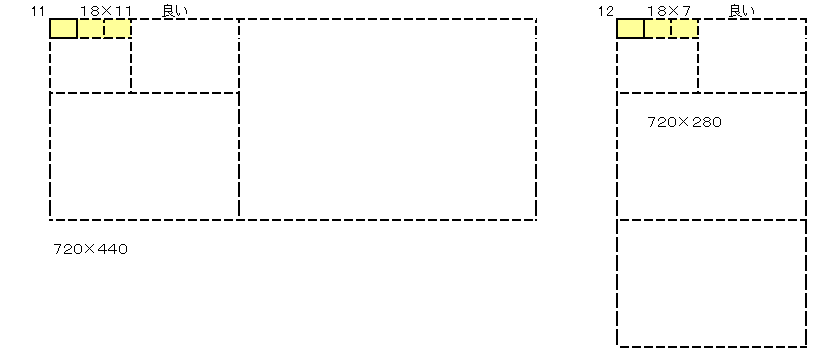
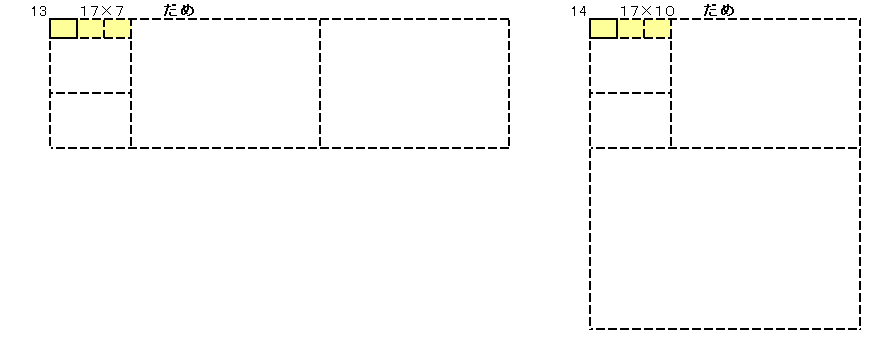
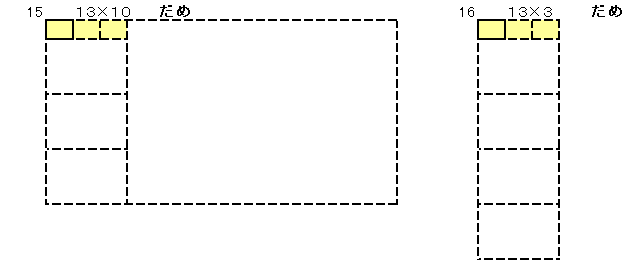
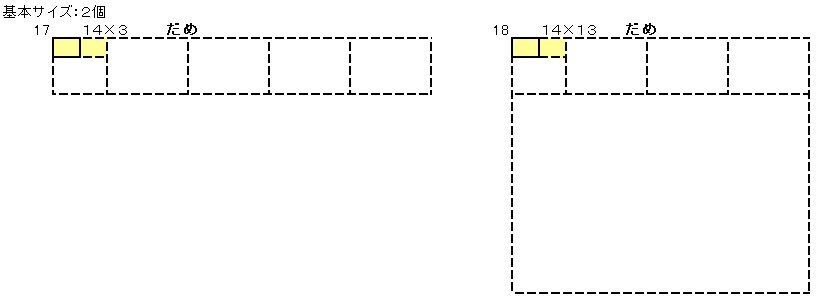

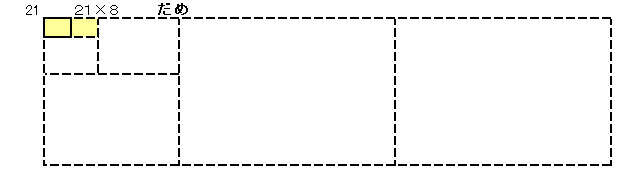
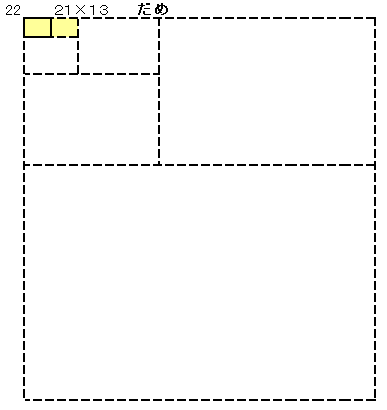

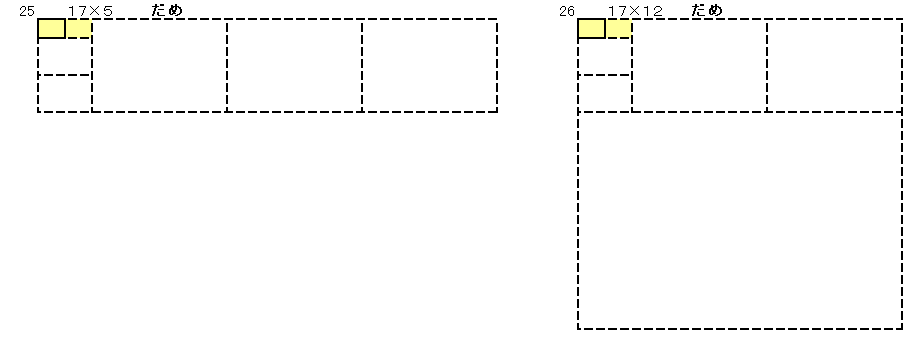
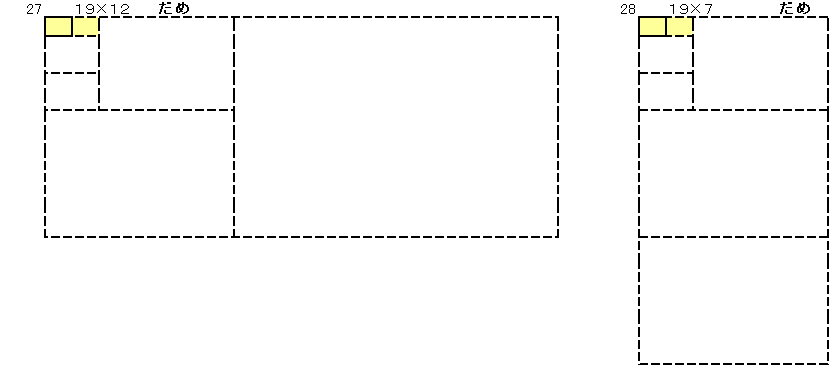
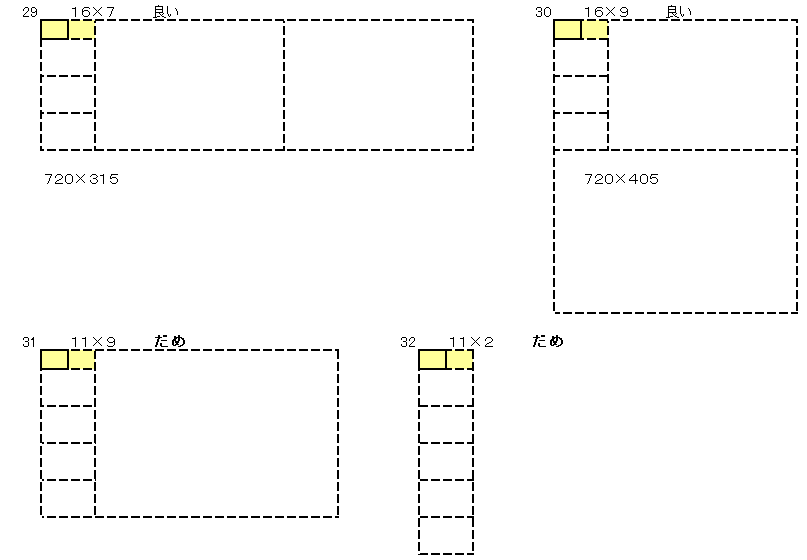
�E����10
�i�y���l�|���F�̂�����j
�i1�j
233��144��1�@�]��89
144��89���P�@�]��55
89��55��1�@�]��34
55��34��1�@�]��21
34��21��1�@�]��13
21��13��1�@�]��8
13��8��1�@�]��5
8��5��1�@�]��3
5��3��1�@�]��2
3��2��1�@�]��1
2��1��2
���̘a��12�A�܂萳���`��12�ł���
����đϐ��́@12�|1��11�@�@�@��{�T�C�Y��1
�i�]�肪�t�B�{�i�b�`����ɂȂ��Ă��Ă������I�j
�i233�͑f���������{�T�C�Y1�͓�����O�Ƃ����Γ�����O�j
�i2�j
�ϐ���6������A�����`��7�ł���
�܂芄��Z�����Ă��������̏��̘a��7�ɂȂ�悢
����Z�̉́A720��7�̔{���ł͂Ȃ�����1��Ƃ������Ƃ͂Ȃ��A
�܂��A�Ō�̏���1�Ƃ������Ƃ͂��肦�Ȃ�����7��Ƃ������Ƃ��Ȃ��B
�܂芄��Z�̉�2�`6��ƍl���Ă悢�B
�]���Ď��R�������Ƃ��āA
�@�@���{����7�A���{���{����7�A���{���{���{����7�A
�@�@���{���{���{���{����7�A���{���{���{���{���{����7
�ƂȂ�悢�B��������̂́A�Ō�̏���1�ɂȂ邱�Ƃ͂Ȃ����玟��31�ʂ�
�@�@1�|6�A2�|5�A3�|4�A4�|3�A5�|2
�@�@1�|1�|5�A1�|2�|4�A2�|1�|4�A1�|4�|2�A4�|1�|2�A
�@�@1�|3�|3�A3�|1�|3�A2�|2�|3�A2�|3�|2�A3�|2�|2�A
�@�@1�|1�|1�|4�A1�|1�|2�|3�A1�|2�|1�|3�A2�|1�|1�|3�A1�|1�|3�|2�A
�@�@1�|3�|1�|2�A3�|1�|1�|2�A1�|2�|2�|2�A2�|1�|2�|2�A2�|2�|1�|2�A
�@�@1�|1�|1�|1�|3�A1�|1�|1�|2�|2�A1�|1�|2�|1�|2�A
�@�@1�|2�|1�|1�|2�A2�|1�|1�|1�|2�A1�|1�|1�|1�|1�|2
�e�X�ɂ��ē_������Ɓi���ꂪ��ςȍ�Ƃł��j
�@�@�i�_����j1�|6�̎�
�@�@�@�@720��x��1�@�]��a
�@�@�@�@�@x��a��6�@�@x��6a������@720��x�{a��7a�E�E�E�E�E�~
��ӂ����͎̂���8�ʂ�
�y�P�z3�|1�|3�@�@���̎���192
�y�Q�z2�|3�|2�@�@�@�@�V�@�@315
�y�R�z1�|2�|1�|3�@�@�@�@�V�@528
�y�S�z2�|1�|1�|3�@�@�@�@�V�@280
�y�T�z1�|1�|3�|2�@�@�@�@�V�@405
�y�U�z3�|1�|1�|2�@�@�@�@�V�@200
�y�V�z1�|1�|1�|1�|3�@�@�V�@440
�y�W�z1�|2�|1�|1�|2�@�@�V�@520
�����8��
�i3�j
800��25�E52
��{�T�C�Y��2�Ƃ������Ƃ͍ő����2�Ƃ������Ƃ�����
�y�P�z�u2�E��v�ƂȂ��Ă�����̂̌��𐔂���
�@�@�@2�A6�A10�A14�A�E�E�E
�@�@�@4n-2��800�@��肻�̐���200
�y�Q�z���̂����A5�̔{���ƂȂ��Ă�����̂�����
�@�@�@10�A30�A50�A�E�E�E
�@�@�@20n-10��800�@��肻�̐���40
�@�@����ē����́@200�|40��160�i�j
(4)
�i321�|1�j���i318�|1�j��33�@�]��33�|1
�i318�|1�j�́i36�|1�j�Ƃ������q�������A
�i36�|1�j�͂܂��A�i33�|1�j�Ƃ������q��������A
�i318�|1�j�́i33�|1�j�Ŋ�����
����Ċ�{�T�C�Y��33�|1��26
���w�炵�������o���Ă������������ƂɊ��ӂ��Ă��܂��I
�E����11
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
����
���P�D�P�P�ł��B�@���Q�D�W�ł��B�@���R�D�P�U�O�ł��B�@���S�D��{�T�C�Y�͂Q�U�ł��B
���P
�b�`�r�h�n�@�e�w�@�W�V�O�o�Ńv���O�������������܂����B�@���̒ʂ�ł��B
�P�O�@�m���O
�Q�O�@�h�m�o�t�s�h�^�e�n �H�h�C�w
�R�O�@�h�m�o�t�s�h���R�n�@�H�h�C �x
�S�O�@�h�e�@�w���x�@�s�g�d�m�@�w���w�|�x�@�d�k�r�d�@�x���x�|�w
�T�O�@�h�e�@�w���x�@�s�g�d�m�@�m���m�{�P�@�F�f�n�s�n�@�W�O
�U�O�@�m���m�{�P
�V�O�@�f�n�s�n�@�S�O
�W�O�@�o�q�h�m�s�h�^�C�X�E���h�G�m�G�h�L�z���T�C�Y���h�G�w
�X�O�@�f�n�s�n�@�P�O
�w�ɂP�S�S�Ɠ��͂���B�x�ɂQ�R�R�Ɠ��͂���B���ʎ��̓������\������܂����B���́@�ϐ����P�P�@��{�T�C�Y���P�ƂȂ�܂��B
���Q
��{�T�C�Y�P�A�����V�Q�O�ɂ���
| �@ | �P�ϐ� | �Q�ϐ� | �R�ϐ� | �S�ϐ� | �T�ϐ� | (�@�U�@�ρ@��)�@ |
|---|---|---|---|---|---|---|
| �i�P�C�P�j | �i�P�C�Q�j | �i�P�C�R�j | �i�P�C�S�j | �i�P�C�T�j | �i�P�C�U�j | �i�P�C�V�j�i�U�C�V�j |
| �@ | �@ | �i�Q�C�R�j | �i�R�C�S�j | �i�S�C�T�j | �i�T�C�U�j | �i�T�C�P�P�j�i�U�C�P�P�j |
| �@ | �@ | �@ | �i�Q�C�T�j | �i�R�C�V�j | �i�S�C�X�j | �i�S�C�P�R�j�i�X�C�P�R�j |
| �@ | �@ | �@ | �i�R�C�T�j | �i�S�C�V�j | �i�T�C�X�j | �i�T�C�P�S�j�i�X�C�P�S�j |
| �@ | �@ | �@ | �@ | �i�Q�C�V�j | �i�R�C�P�O�j | �i�R�C�P�R�j�i�P�O�C�P�R�j |
| �@ | �@ | �@ | �@ | �i�T�C�V�j | �i�V�C�P�O�j | �i�V�C�P�V�j�i�P�O�C�P�V�j |
| �@ | �@ | �@ | �@ | �i�R�C�W�j | �i�S�C�P�P�j | �i�S�C�P�T�j�i�P�P�C�P�T�j |
| �@ | �@ | �@ | �@ | �i�T�C�W�j | �i�V�C�P�P�j | �i�V�C�P�W�j�i�P�P�C�P�W�j |
| �@ | �@ | �@ | �@ | �@ | �i�Q�C�X�j | �i�Q�C�P�P�j�i�X�C�P�P�j |
| �@ | �@ | �@ | �@ | �@ | �i�V�C�X�j | �i�V�C�P�U�j�i�X�C�P�U�j |
| �@ | �@ | �@ | �@ | �@ | �i�T�C�P�Q�j | �i�T�C�P�V�j�i�P�Q�C�P�V�j |
| �@ | �@ | �@ | �@ | �@ | �i�V�C�P�Q�j | �i�V�C�P�X�j�i�P�Q�C�P�X�j |
| �@ | �@ | �@ | �@ | �@ | �i�R�C�P�P�j | �i�R�C�P�S�j�i�P�P�C�P�S�j |
| �@ | �@ | �@ | �@ | �@ | �i�W�C�P�P�j | �i�W�C�P�X�j�i�P�P�C�P�X�j |
| �@ | �@ | �@ | �@ | �@ | �i�T�C�P�R�j | �i�T�C�P�W�j�i�P�R�C�P�W�j |
| �@ | �@ | �@ | �@ | �@ | �i�W�C�P�R�j | �i�W�C�Q�P�j�i�P�R�C�Q�P�j |
�@�@ ���̒��łU�ϐ��̉E���̐����V�C�P�P�C�P�R�C�P�S�C�P�V�C�P�T�C�P�W�C�P�P�C�P�U�C �P�X�C�Q�P�łV�Q�O�����Z�������ʐ����ɂȂ鐔�͂P�T�C�P�U�C�P�W�ł��B �]���Ă��̌��͂W�ł��B
���R
�W�O�O�̊�{�T�C�Y�Q���k�����ĂS�O�O�̊�{�T�C�Y�P�Ƃ��čő�����v�Z���܂����B
���P�����P�C�R�C�V�C�X��������̂��ő���̎��R���Ȃ̂Ŏ��̎��Ōv�Z���܂��B
�S�O�O���P�O�~�S���P�U�O�ł��B
���S
�R�Q�P�|�P�ƂR�P�W�|�P�@�̍ő�������߂܂��B
�R�i�@�ŕ\������ƂQ�̐��͔{���ł��鎖��������܂��B�]���Ă��̍ő����
�R�i�@�̂Q�̌����v�Z���܂��B
�Q�O�|�P�V���R�@�P�O�i�@�ɒ����ƂR�R�|�P���Q�U�ł��B��{�T�C�Y�Q�U�ł��B
�E����12
�i�y���l�|���F�q���N�����E�������W���j
(1)�ϐ��F�P�P�A��{�T�C�Y�F�P
�����`�̊e�ӂ̒�����(���C��)�̌`�ŕ\������B
�i�P�S�S�C�Q�R�R�j
�i�P�S�S�C�W�X�j
�i�T�T�C�W�X�j
�i�T�T�C�R�S�j
�i�Q�P�C�R�S�j
�i�Q�P�C�P�R�j
�i�W�C�P�R�j
�i�W�C�T�j
�i�R�C�T�j
�i�R�C�Q�j
�i�P�C�Q�j
�i�P�C�P�j
(2)�W��
�U��̍�Ƃ��I�������Ԃ���A�����̂ڂ��Ă݂�B
�U��̍�ƏI�����_�̐����`�̈�ӂ����Ƃ����B
�i���C���j
�T��̍�ƏI����
�@�i�Q���C���j
�S��̍�ƏI����
�@�i�R���C���j�C�i�R���C�Q���j
�R��̍�ƏI����
�@�i�S���C���j�C�i�S���C�R���j�C�i�T���C�Q���j�C�i�T���C�R���j
�Q��̍�ƏI����
�@�i�T���C���j�C�i�T���C�S���j�C�i�V���C�S���j�C�i�V���C�R���j�C�i�V���C�T���j�C�i�V���C�Q���j�C
�@�i�W���C�T���j�C�i�W���C�R���j
�P��̍�ƏI����
�@�i�U���C�T���j�C�i�U���C���j�C�i�X���C�T���j�C�i�X���C�S���j�C�i�P�P���C�V���j�C�i�P�P���C�S���j�C
�@�i�P�O���C�V���j�C�i�P�O���C�R���j�C�i�P�Q���C�V���j�C�i�P�Q���C�T���j�C�i�X���C�V���j�C�i�X���C�Q���j�C
�@�i�P�R���C�W���j�C�i�P�R���C�T���j�C�i�P�P���C�W���j�C�i�P�P���C�R���j
���Ƃ̒����`
�@�i�P�P���C�U���j�C�i�P�P���C�T���j�C�i�V���C�U���j�C�i�V���C���j�C�i�P�S���C�X���j�C�i�P�S���C�T���j�C
�@�i�P�R���C�X���j�C�i�P�R���C�S���j�C�i�P�W���C�P�P���j�C�i�P�W���C�V���j�C�i�P�T���C�P�P���j�C�i�P�T���C�S���j�C
�@�i�P�V���C�P�O���j�C�i�P�V���C�V���j�C�i�P�R���C�P�O���j�C�i�P�R���C�R���j�C�i�P�X���C�P�Q���j�C�i1�X���C�V���j�C
�@�i�P�V���C�P�Q���j�C�i�P�V���C�T���j�C�i�P�U���C�X���j�C�i�P�U���C�V���j�C�i�P�P���C�X���j�C�i�P�P���C�Q���j�C
�@�i�Q�P���C�P�R���j�C�i�Q�P���C�W���j�C�i�P�W���C�P�R���j�C�i�P�W���C�T���j�C�i�P�X���C�P�P���j�C�i�P�X���C�W���j�C
�@�i�P�S���C�P�P���j�C�i�P�S���C�R���j
���̂����A���ӂ��V�Q�O�̏����ɍ����̂́A
�@�i�P�W���C�P�P���j�C�i�P�W���C�V���j�C�i�P�T���C�P�P���j�C�i�P�T���C�S���j�C
�@�i�P�U���C�X���j�C�i�P�U���C�V���j�C�i�P�W���C�P�R���j�C�i�P�W���C�T���j�̂W��
(3) �P�U�O��
��{�T�C�Y�̑傫���́A�����`�̂Q�ӂ̍ő���ɂȂ�B
�W�O�O�������������ŁA�W�O�O�Ƃ̍ő�����Q�ɂȂ���̂��l����B
���߂鐔�́A�Q�~�` �Ƃ���킹��B
�������A�`�͂S�O�O��菬�����A�Q�ł��T�ł�����Ȃ����B�Ȃ��Ȃ�A
�@�@�W�O�O���Q�~�Q�~�Q�~�Q�~�Q�~�T�~�T
�Ȃ̂ŁB�R�X�X�ȉ��̐����łQ�ł��T�ł�����Ȃ����̂̌��́A�P�U�O�B
(4) �Q�U
(�R�Q�P�|�P)��(�R�P�W�|�P)�̍ŏ����{�������߂�B
�@(�R�Q�P�|�P)�~(�R�P�W�|�P)
�@(�i�R�R)�V�|�P�j�~((�R�R)�U�|�P)
�@(�Q�V�V�|�P�j�~(�Q�V�U�|�P)
�����ň��A�����`�����ƁA
�@(�Q�V�V�|�Q�V�U�j�~(�Q�V�U�|�P)
�@�Q�V�U(�Q�V�|�P�j�~(�Q�V�U�|�P)
�@�Q�V�U(�Q�U�j�~(�Q�V�U�|�P)
�����ʼnE�ӂ�������������
�@�Q�V�U(�Q�U�j�~(�Q�V�R�|�P)(�Q�V�R�{�P)
�@�Q�V�U(�Q�U�j�~(�Q�V�|�P)(�Q�V�Q�{�Q�V�{�P)(�Q�V�{�P)(�Q�V�Q�|�Q�V�{�P)
�@�Q�V�U(�Q�U�j�~(�Q�U)(�V�T�V)(�Q�W)(�V�O�R)
����āA�ő���͂Q�U
�E����13
�i�y���l�|���F�o���^�����l�j
����́A���\hard�ł����B
(1) ���� �ϐ��P�P�A��{�T�C�Y�P
233�A89�A34�A13�A5�A2�A1
144�A55�A21�A 8�A3�A1
���ɍl���܂����B�t���猩��ƑO�Q���̘a�ƂȂ�t�B�{�i�b�`����ł��ˁB
(2)�����W
�t��(1,1)����U��̑�����l���܂����B�P��ڂ�(1,2)�����B
�Q��ڂ�1+2=3��1�܂���2�ƒu�������B���̂悤�ɂ����32�ʂ�ł���B
�S�Ă����߁A���̂����傫������720�̖ł�����̂�I�т܂����B
(4,15)�~48�@�P�X�Q�@�@(11,15)�~48�@�T�Q�W
(7,18)�~40�@�Q�W�O�@�@(11,18)�~40�@�S�S�O
(7,16)�~45�@�R�P�T�@�@( 9,16)�~45�@�S�O�T
(5,18)�~40�@�Q�O�O�@�@(13,18)�~40�@�T�Q�O
(3) �����P�U�O��
���ӂW�O�O�A��{�T�C�Y�Q�̑g�ݍ��킹�́A���ӂS�O�O�A��{�T�C�Y�P��
���͓����B���ӂƒZ�ӂ��������Ƃ��A��{�T�C�Y��(�ő�)����
�Ȃ�̂Ŋ�{�T�C�Y���P�ƂȂ�݂̂͌��ɑf�Ȏ��B
�S�O�O�͂Q�S�~�T�Q�Ȃ̂łP�`�S�O�O�ŁA�Q�y�тT�̖������Ȃ�
�������߂�悢�B
�Q�̖Q�O�O�A�T�̖W�O�A�P�O�̖S�O��
�S�O�O�|�i�Q�O�O�{�W�O�|�S�O�j���P�U�O
(4)�����Q�U
�@�@�@ (�R�Q�P�|�P)���Q�V�~(�R�P�W�|�P)�{�Q�U
�Q�V��̑���ŒZ�ӂ͂Q�U�ɂȂ�B
�@�@�@(�R�P�W�|�P)��(�R�U�|�P)�~(�R�P�Q�{�R�U�{�P)
�@�@��(�R�R�|�P)�~(�R�R�{�P)�~(�R�P�Q�{�R�U�{�P)
�@�@���Q�U�~�Q�W�~�i�V�Q�X�~�V�Q�X�{�V�Q�X�{�P�j
�Q�U�̔{���ƂȂ�̂Ŋ�{�T�C�Y�͂Q�U
�ԈႦ�đϐ��܂ŋ��߂Ă��܂���ςł����B
�E����14
�i�y���l�|���F�J�̖��j
�i1�j��ӂ��
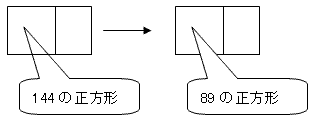
�ƌ����悤�ɏ��������`������Ă�����11��ڂ�1�̐����`�ƂȂ�B�����āA�ϐ���11�A��{�T�C�Y1�ƂȂ�B
���AA�~B�̒����`��A��B��ω������A���s������J��Ԃ��ƁA��{�T�C�Y�͐�A��B�̍ő���ł��邱�Ƃ��m���߂���B
�i2�j�i1�j�̋t�����݂�B���A�����ӂ�B�A�Z���ӂ�A�Ƃ��A���̑���ɂ��o���钷���`���iA,B�j�ƕ\���ƁA

������i1,7�j�i6,7�j�Ȃǂ��ł��������̕�720�̖ł���i4,15�j�i11,15�j�Ȃ�8�ƂȂ鎖��������B
�i3�j�i1�j�̎��s����̌��ʂ��ő����2�ł���Ηǂ��B �����A400�܂ł̐��̂����A��ł��邱�Ƃ��K�v�B �A���A������5�ł���ƍő����5�Ŗ����Ȃ邽��1,3,7�y��9�łȂ���Ȃ�Ȃ��B �����āA400�~4/10��160�����߂���̂ł���B
�i4�j����܂ł̋c�_���痼�ӂ̍ő�������߂�Ηǂ��B
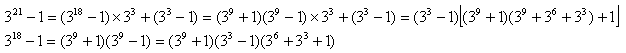
�����āA�����2���̍ő���� �ƂȂ�B�������{�T�C�Y��26�ł���B
�E����15
�i�y���l�|���FToru�j
����͑S�����[�N���b�h�̌ݏ��@�ł��ˁB����Ȃ̂����w���w�Ƃ͍l�����܂���
���B
(1)
�@144x233��144x89��55x89��55x34��21x34��21x13��8x13��8x5��3x5��3x2��1x2��1x1
���ϐ��͂P�P�@��{�T�C�Y�͂P
(2)
1x1����t�ɐ����`���������Ă����ƂQ��ڈȍ~�͏c�ɂ��邩���ɂ��邩
�ŁA�Q�ʂ肸����
�@0) 1x1
�@1) 1x2
�@2) 1x3,3x2
�@3) 1x4,4x3,3x5,5x2
�@4) 1x5,5x4,4x7,7x3,3x8,8x5,5x7,7x2
�@5) 1x6,6x5,5x9,9x4,4x11,11x7,7x10,10x3,3x11,11x8,8x13,13x5,5x12,12x7,7x9,9x2
�@6) 1x7,7x6,6x11,11x5,5x14,14x9,9x13,13x4,4x15,15x11,11x18,18x7,7x17,17x10,10x13,
�@�@13x10,3x14,14x3,11x19,19x8,8x21,21x13,13x18,18x5,5x17,17x12,12x19,19x7,7x16,
�@�@16x9,9x11,11x2
�̂R�Q�ʂ�̉\�������邪�A���������V�Q�O�̖łȂ���Ȃ�Ȃ��̂�
�@720=24x32x5 ���
4x15,15x11,11x18,18x7,13x18,18x5 ,7x16,16x9�̂W�ʂ肪����B
���ꂼ��A�Z�����̕Ӂi��{�T�C�Y�j
192(48),528(48), 440(40),280(40),520(40),200(40),315(45),405(45)
(3)
800 �Ŋ�{�T�C�Y���Q�ł��邩�� 400�łP�@400�Ƒf�Ȑ��𐔂���悢
��(400)=��(24x52)=400(1-1/2)(1-1/5)=160�@�i�ӂ̓I�C���[���j
(4)
321-1��318-1�̍ő�������߂�B
(321-1,318-1)
=(321-1-33(318-1),318-1)=(33-1,318-1)=33-1=26
������
| �o���^�����l | �̂����� | Toru |
| �q���N�����E�������W�� | �J�̖� | ��ӂ����̂炢�������� |
| ���C | �]�ʔ��� | �X���[�N�}�� |
| ��̂������� | ���܂����R | nao |
| �O�p��K | �e���X�ƃA���X | kohji |
�܂Ƃ�
�����̖��́A���[�N���b�h�̌ݏ��@���e�[�}�̖��ł������A������ƃn�[�h�ł����ł��傤���B
���[�N���b�h�̌ݏ��@�ɂ��ẮA��ӂ����̂炢�������������������Ă��������Ă��܂��B
�i�P�j�ɂ���P�S�S�A�Q�R�R�Ƃ��������́A�ׂ荇�����t�B�{�i�b�`���ł��ˁB
�̂������̂��w�E�ɂȂ�悤�ɁA���̑�����J��Ԃ��ƁA
�t�B�{�i�b�`����������̂ڂ邱�ƂɂȂ�܂��B
�������낢�ł��ˁB
�i�Q�j�Ō˘f���Ă�����������������悤�Ɏv���܂����A
���̑�����J��Ԃ��ƁA�ŏI�I�ɂ́A
�q���N�����E�������W�������̉ɂ���悤�ɁA���~���̐����`�ɂȂ�܂�����A
�������炳���̂ڂ��Ă����Ƃ悢�̂ł͂Ȃ��ł��傤���B������ɂ��Ă��A�R��Ȃ��T���Ă��������Ȃ��̂��ȂƎv���܂��B
 top
top