侾俀俈丏僇儗儞僟乕偺栤戣
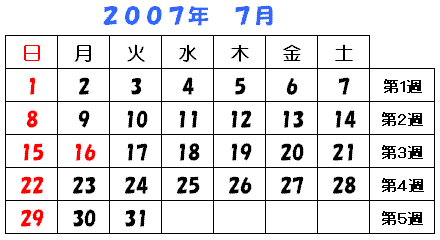
壓偼2007擭俈寧偺僇儗儞僟乕偱偡丅僞僇僔孨偼偙偺俈寧偵偼枅廡侾夞偢偮崌寁俆夞偺
僒僢僇乕偺帋崌傪偟傑偡丅帋崌偺梛擔偼寧梛擔偑侾夞丄悈梛擔偑俀夞丄搚梛擔偑侾夞丄
擔梛擔偑侾夞偱偡丅僞僇僔孨偑僒僢僇乕傪偡傞擔晅偺悢偺榓偼偄偔偮偱偡偐丅
栤戣偺弌揟
峀拞攖僴僀儗儀儖拞妛悢妛偵挧愴
嶼悢僆儕儞僺僢僋埾堳夛娔廋
島択幮僽儖乕僶僢僋僗
2002擭僩儔僀儎儖栤戣夵戣
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗塝搰屲榊乯
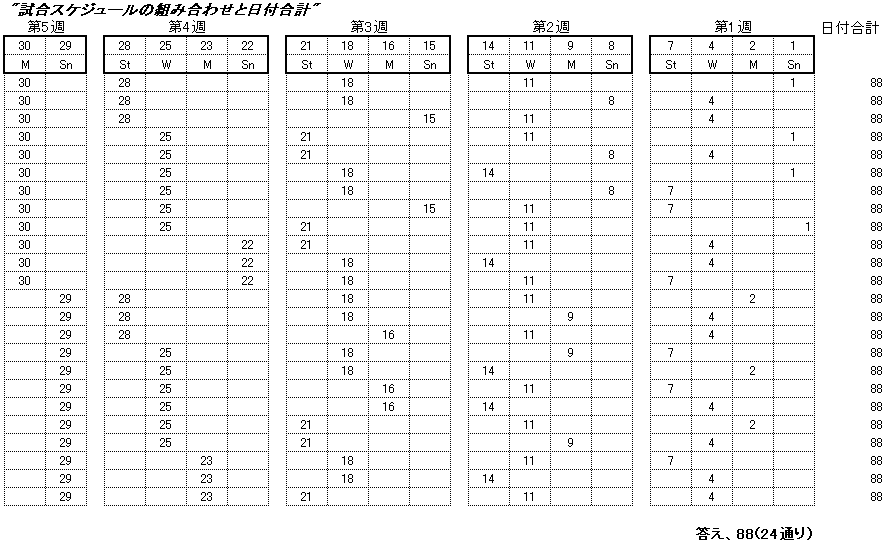
夝摎丒偦偺2
乮儁儞僱亅儉丗偺偭偙傫乯
(1)29擔乮擔乯偵帋崌偑偁傞
丂寧丒丒丒2丂 9丂16丂23
丂悈丒丒丒4丂11丂18丂25
丂搚丒丒丒7丂14丂21丂28
悈偺帋崌傪4丂11偲偡傞偲
16丂28偵帋崌傪偡傞偐丄21丂23偵帋崌傪偡傞偐偵側傞偑
偄偢傟偵偟偰傕丄
寧亄搚亖44丂丂
寧亄悈亄悈亄搚亖59
擔亄寧亄悈亄悈亄搚亖88丂偲側傞
悈偺慖傃曽偼4C2亖6捠傝偁傞偑丄偄偢傟傕憤榓偼88偱偁傞
(2)30擔乮寧乯偵帋崌偑偁傞
丂擔丒丒丒1丂 8丂15丂22
丂悈丒丒丒4丂11丂18丂25
丂搚丒丒丒7丂14丂21丂28
悈偺帋崌傪4丂11偲偡傞偲
15丂28偵帋崌傪偡傞偐丄21丂22偵帋崌傪偡傞偐偵側傞偑
偄偢傟偵偟偰傕丄
擔亄搚亖43丂丂
擔亄悈亄悈亄搚亖58
擔亄寧亄悈亄悈亄搚亖88丂偲側傞
悈偺慖傃曽偼4C2亖6捠傝偁傞偑丄偄偢傟傕憤榓偼88偱偁傞
乮摎乯88丂
夝摎丒偦偺3
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
戞屲廡偼擔梛偐寧梛偟偐偱偒側偄丅
29乮擔乯偲偡傞偲偒丄
寧偺岓曗偼丄29-a*7+1丒丒丒a=1乣4
悈偺岓曗偼丄29-b*7+3丒丒丒b=a偲堎側傞1乣4偺偆偪偺2屄
搚偺岓曗偼丄29-c*7+6丒丒丒c=a,b 偲堎側傞1乣4
偮傑傝丄偡傋偰懌偡偲丄29*5-7*儼(1乣4)+13=29*5-70+13=88
30乮寧乯偺偲偒丄
擔偺岓曗偼丄30-a*7-1
悈偺岓曗偼丄30-b*7+2
搚偺岓曗偼丄30-c*7+5
偡傋偰懌偡偲丄30*5-7*儼(1乣4)+8=150-70+8=88
壗傟偵偣傛摨偠偔88丂
夝摎丒偦偺4
乮儁儞僱亅儉丗揮埵斀墳乯
愭偢丄枅廡丄帋崌偑奐嵜偝傟傞偙偲偐傜丄戞俆廡偵偮偄偰偼俀俋擔偺擔梛擔丄傑偨偼
俁侽擔偺寧梛擔偺奐嵜偑昁梫偲側傞丅
傑偨丄戞侾廡偐傜戞係廡偺奺梛擔偺擔晅偼丄埲壓偺傛偆偵昞尰偱偒傞丅
擔梛擔偺擔晅亖侾亄俈(値亅侾乯
寧梛擔偺擔晅亖俀亄俈(値亅侾乯
悈梛擔偺擔晅亖係亄俈(値亅侾乯
搚梛擔偺擔晅亖俈亄俈(値亅侾乯 丄扐偟丄 値亖侾丆俀丆俁丆係
偝偰丄働乕僗偛偲偵擔晅偺崌寁傪媮傔傞丅
働乕僗嘥丗擔梛擔奐嵜偑俀俋擔偺応崌
枅廡奐嵜偲偟偰堦斒惈傪幐傢側偄傛偆偵丄値亖p丆q丆r丆s偲抲偔丅丂倫亗倯亗倰亗倱
| 擔晅偺崌寁 | |
| 亖 | 俀俋+乲俀亄俈(倫亅侾乯乴亄乲係亄俈(倯亅侾乯乴亄乲係亄俈(r亅侾乯乴亄乲俈亄俈(s亅侾乯乴 |
| 亖 | (倫亄倯亄倰亄倱乯亄侾俉 |
| 亖 | 俉俉 |
摨條偵偟偰丄
働乕僗嘦丗寧梛擔奐嵜偑俁侽擔偺応崌
| 擔晅偺崌寁 | |
| 亖 | 俁侽+乲侾亄俈(倫亅侾乯乴亄乲係亄俈(倯亅侾乯乴亄乲係亄俈(r亅侾乯乴亄乲俈亄俈(s亅侾乯乴 |
| 亖 | 俈(倫亄倯亄倰亄倱乯亄侾俉 |
| 亖 | 俉俉 |
夝摎丒偦偺5
乮儁儞僱亅儉丗俥倎倳倱俿乯
偊乣偲丄側偵側偵丠
壗擔偐偼傢偐傜側偄偗偳丄寧侾丄悈俀丄搚侾丄擔侾偺俆偮偺擔晅偺崌寁偼偄偔偮偵側傞偐丠偭偰栤戣偩傛偹丠
偳偺廡偵偳偺梛擔偵側傞偐偵傛偭偰崌寁悢偑堘偭偰偔傞丒丒丒傛偆側婥偑偡傞側偀丅
偲偄偆偙偲偱丄幚嵺偵偄偔偮偐傗偭偰傒傟偽丄偦偺朄懃惈偱傕尒偮偗傜傟傞偐側丠憗懍傗偭偰傒傛偆丅
傑偢偼丄戞堦廡栚乣戞屲廡栚偵忋婰偺弴偵廩偰偰偄偙偆丅
偡傞偲丒丒丒俀擔丄侾侾擔丄侾俉擔丄俀俉擔丄俀俋擔丅偙傟傜傪崌寁偡傞偲丒丒丒俉俉擔丅
偝偰丄崱搙偼媡偵戞屲廡栚乣戞堦廡栚偵弴偵廩偰偰偄偙偆偐丅
偡傞偲丒丒丒俁侽擔丄俀俆擔丄侾俉擔丄侾係擔丄侾擔丅偙傟傜偺崌寁偼丒丒丒偊乣偲丄
偁傟偭丠俉俉擔両丠摨偠偵側偭偨偗偳丄偙傟偼嬼慠偐昁慠偐丠
偦偆偐両
偳偆傗傜偳偺廡偺偳偺梛擔偺慻傒崌傢偣偵側偭偰傕丄崌寁偑俉俉擔偵側傞傛偆側婥偑偟偰偒偨偧丅
偁偲偼偙偺偙偲傪帵偣偽偄偄偺偐側丅
丒丒丒偲偄偆偙偲偱丄徹柧丅
慖戰偡傞俆偮偺擔偼丄戞堦廡栚乣戞屲廡栚偺偦傟偧傟偺廡偺偄偢傟偐偺擔偱偁傞偺偱丄
廡偺嵟弶偱偁傞擔梛擔偺悢偵寧梛側傜侾丄悈梛側傜俁偲偄偆傛偆偵奩摉偡傞梛擔偵懳偟偰悢傪懌偣偽偄偄偺偐側丅
俀侽侽俈擭俈寧偺擔梛偼丄侾擔丄俉擔丄侾俆擔丄俀俀擔丄俀俋擔偱偁傝丄
偙偺偦傟偧傟偵梛擔偵奩摉偡傞悢亙寧梛亖侾丄悈梛亖俁乮悈梛偼俀廡偁傞乯丄搚梛亖俇丄擔梛亖侽亜
傪弴晄摨偱壛偊傞偙偲偵側傞偺偱丄媮傔傞崌寁悢偼丄
丂丂丂乮侾亄俉亄侾俆亄俀俀亄俀俋乯亄乮侾亄俁亄俁亄俇亄侽乯亖丂俉俉
傛偭偰丄偳偺廡偺偳偺梛擔偺慻傒崌傢偣偱傕崌寁悢偼俉俉擔偲側傞丅
丒丒丒偙傫側傫偱徹柧偟偨偙偲偵側傞偐側丠
傑丄偲偵偐偔丄摎偊偼丂亂丂俉俉擔丂亃丂偱娫堘偄側偝偦偆偱偡偹丅丂丂乮丂埲丂忋丂乯
夝摎丒偦偺6
乮儁儞僱亅儉丗傑偡傑偡僞僐偝傫乯
夝摎丗俉俉
夁掱丗嵟弶偵丄嵟廔廡偼壩梛擔傑偱偟偐偁傝傑偣傫偺偱丄擔梛擔偐寧梛擔偵側傝傑偡丅
偲傝偁偊偢丄揔摉偵僗働僕儏乕儖傪慻傫偱傒傑偟傚偆丅
僞僇僔孨偑旀傟傞偲偄偗側偄偺偱丄擇擔楢懕偵側傜側偄傛偆偵偟傑偡丅
乮偲偔偵怺偄堄枴偼偁傝傑偣傫乯
堦廡栚丂悈梛擔丂丂係擔
擇廡栚丂搚梛擔丂侾係擔
嶰廡栚丂悈梛擔丂侾俉擔
巐廡栚丂寧梛擔丂俀俁擔
屲廡栚丂擔梛擔丂俀俋擔
偲偡傞偲丄係亄侾係亄侾俉亄俀俁亄俀俋偱丄俉俉偵側傝傑偡丅
懠偺慻傒崌傢偣乮擔掱乯偼偳偆側傞偱偟傚偆丅
嶰廡栚偲巐廡栚偺梛擔乮擔偵偪乯傪擖傟懼偊偰傒傑偟傚偆丅
係擔丄侾係擔丄侾俇擔丄俀俆擔丄俀俋擔偲側傝丄
係亄侾係亄侾俇亄俀俆亄俀俋偱丄俉俉偵側傝傑偡丅偍傗丠
偳偆傗傜丄忦審捠傝偵擔掱傪慻傓偲丄崌寁偼偳傟傕乽俉俉乿偵側傝偦偆偱偡丅
梛擔偛偲悢帤傪値傪巊偭偰昞尰偡傞偲丄
寧梛擔偼丄乮俀亄俈値乯擔
悈梛擔偼丄乮係亄俈値乯擔
搚梛擔偼丄乮俈亄俈値乯擔
擔梛擔偼丄乮侾亄俈値乯擔
悈梛擔偵帋崌偑擇夞偁偭偰丄奺廡堦夞偱偡偐傜丄帋崌擔偺悢帤偺崌寁偼丄
丂丂丂乮俀亄俈値乯亄乮係亄俈値乯亄乮係亄俈値乯亄乮俈亄俈値乯亄乮侾亄俈値乯
偵側傝傑偡丅偙偙偱丄値偵偼丄侽乣係偑堦夞偢偮擖傝傑偡丅惍棟偡傞偲丄
丂丂丂俀亄係亄係亄俈亄侾亄乮俈亊乮侽亄侾亄俀亄俁亄係乯乯亖侾俉亄俈侽亖俉俉
偲側傝丄壗廡栚偺壗梛擔偵帋崌傪偟偰傕丄忦審捠傝側傜丄俉俉偵側傝傑偡丅
夝摎丒偦偺7
乮儁儞僱亅儉丗僥儗僗偲傾儕僗乯
亂夝摎亃
戞侾廡偐傜戞俆廡偺偦傟偧傟偺嵟弶偺擔乮擔梛擔乯乮1丄8丄15丄22丄29乯傪儀乕僗偲偟偰丄
戞壗廡偑丂寧丄悈丄搚梛擔偺偳傟偱偁偭偰傕乮戞5廡偼悈梛丄搚梛偼偁傝傑偣傫偑乯丄
寧梛擔丄悈梛擔丄搚梛擔偼偦傟偧傟丄亄1擔丄亄3擔丄亄6擔偲偟偰峫偊傞偙偲偱媮傑傝傑偡丅
丂丂丂乮1 亄 8 亄 15 亄 22 亄 29乯 亄 1 亄 3 亄 3 亄 6丂=丂88
摎偊偼丄丂88擔偱偡丅
夝摎丒偦偺8
乮儁儞僱亅儉丗teki乯
摎偊丂丂俉俉擔
奺廡侾夞偢偮帋崌傪偡傞偺偱偡偐傜丄梛擔偑偒傑傟偽弴斣偵娭學側偔
寛傑傝傑偡偹丅
椺偊偽丄戞侾廡偵擔梛丄戞俀丆俁廡偵悈梛丄戞係廡偵搚梛丄戞俆廡偵寧梛
偵帋崌傪偟偰傕丄戞侾廡偵悈梛丄戞俀廡偵搚梛丄戞俁廡偵悈梛丄戞係廡偵寧梛丄
戞俆廡偵擔梛偲偟偰傕丄俉俉擔偱偡丅
夝摎丒偦偺9
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂俉俉偱偡丅
僒僢僇乕傪偡傞擔偼枅廡侾夞偲側偭偰偄傑偡丅廬偭偰戞俆廡傑偱偺擔梛擔偺丂
擔晅偺悢偺崌寁傪寁嶼偟傑偡丅
擔梛擔丂侾丄俉丆侾俆丆俀俀丆俀俋
丂丂丂俆亊乮侾亄俀俋乯乛俀亖俈俆@@丒丂(1)
偙傟偵擔梛擔偐傜偺奺梛擔傑偱偺擔悢傪壛偊傑偡丅
丂寧梛擔丂侾亊侾夞亖侾
丂悈梛擔丂俁亊俀夞亖俇
丂搚梛擔丂俇亊侾夞亖俇
懄偪丂侾亄俇亄俇亖侾俁@@@(2)
崌寁偼(1)亄(2)亖俈俆亄侾俁亖俉俉偲側傝傑偡丅
忦審偵崌偊偽偳偺傛偆側慻崌偣偱傕崌寁偼俉俉偵側傝傑偡丅
夝摎丒偦偺10
乮儁儞僱亅儉丗僸儍僋儗儞丒儔儔儞僕儍乯
摎丗俉俉
峫偊曽丗
偡傋偰偺廡偑擔梛擔偐傜巒傑偭偰偄傞偺偱丄懠偺梛擔傪師偺傛偆偵峫偊傑偡丅
寧梛擔偺擔晅偼丄擔梛擔偺擔晅亄侾擔
悈梛擔偺擔晅偼丄擔梛擔偺擔晅亄俁擔
搚梛擔偺擔晅偼丄擔梛擔偺擔晅亄俇擔
擔梛擔偺擔晅偺崌寁偼丄侾亄俉亄侾俆亄俀俀亄俀俋亖俈俆
僞僇僔孨偼丄寧梛擔(亄侾擔)偑侾夞丄悈梛擔(亄俁擔)偑俀夞丄搚梛擔(亄俇擔)偑侾夞丄擔梛擔(亄侽擔)偑侾夞丅
傛偭偰丄
俈俆亄侾亄俁亊俀亄俇亖俉俉
夝摎丒偦偺11
乮儁儞僱亅儉丗僆儎僕乯
俙侾丆丒丒丒丆俙俆亖乷侽丆俈丆侾係丆俀侾丆俀俉乸偲偡傞丅
帋崌偺偁傞奺梛擔偼丄偦傟偧傟丆壓婰偺傛偆偵昞偡帠偑偱偒傞丅
偨偩偟俙侾乣俙俆偼慡偰堎側傞傕偺偲偡傞丅
丂擔梛擔丂丗俙侾亄侾丂
丂寧梛擔丂丗俙俀亄俀
丂悈梛擔丂丗俙俁亄係丆俙係亄係丂偨偩偟俙俁丆俙係亗俀俉
丂搚梛擔丂丗俙俆亄俈丂丂丂丂丂丂偨偩偟俙俆亗俀俉
廬偭偰媮傔傞悢偼丆
| 乮俙侾亄侾乯亄乮俙俀亄俀乯亄乮俙俁亄係乯亄乮俙係亄係乯亄乮俙俆亄俈乯 | |
| 亖 | 乮俙侾亄俙俀亄俙俁亄俙係亄俙俆乯亄侾俉 |
| 亖 | 俈侽亄侾俉亖俉俉 |
夝摎丒偦偺12
乮儁儞僱亅儉丗偙傑偭偨僐乯
帋崌傪偡傞5擔偺擔晅傪
擔梛擔偺擔晅偼7a-6丄寧梛擔偺擔晅偼7b-5丄悈梛擔偺擔晅偼7c-3, 7d-3丄搚梛擔偼7e
偱昞偡偙偲偵偡傞丅
a乣e偵擖傞悢帤偼偦傟偧傟壗廡栚偐傪昞偡丅
傛偭偰丄a乣e偵偼1乣5偺偄偢傟偐偺悢帤偑擖傞丅
偨偩偟丄摨偠悢帤偑廳暋偟偰擖傞偙偲偼側偄丅
(1廡娫1帋崌側偺偱丄悢帤偑廳暋偡傞偲1廡娫偵2帋崌偡傞偙偲偵側傞偺偱柕弬偟偰偟傑偆丅)
傑偨悈梛擔偲搚梛擔偼4廡栚傑偱偟偐側偄偺偱丂a,b偺偄偢傟偐偵昁偢5偑擖傞偙偲偵側傞丅
偙偺5擔偺擔晅偺悢偺榓側偺偱
丂丂丂7a-6+7b-5+7c-3+7d-3+7e=7(a+b+c+d+e)-17
a=5偺帪丄b,c,d,e偵偼1偐傜4偺偄偢傟偐偑擖傟偽傛偄丅
b=5偺帪丄b,c,d,e偵偼1偐傜4偺偄偢傟偐偑擖傟偽傛偄丅
偲偄偆偙偲偼偄偢傟偺応崌偱傕丄a+b+c+d+e=1+2+3+4+5=15偵側傞丅
偙傟傪忋偺幃偵戙擖偡傞偲7x15-17=88
傛偭偰帋崌傪偡傞擔晅偺悢偺榓偼88丅
夝摎丒偦偺13
乮儁儞僱亅儉丗儗僀乯
幍寧偼堦擔偑擔梛側偺偱丄 奺梛擔偵偮偄偰師偺傛偆偵抣傪掕傔傞
丂Sun = 1, Mon = 2, Tue = 3, Wed = 4, Thu = 5, Fri = 6, Sat = 7
偡傞偲丄廡偛偲偺梛擔偺擔晅偼
7亊(N 廡栚-1) + 忋婰偵掕傔偨梛擔偺抣丂偱媮傑傞
忦審傛傝丄5廡偁傞拞偱奺廡偵 1夞帋崌傪偡傞偺偱丄媮傔傞幃偼師偺條偵側傞
丂7亊(1-1) + 7亊(2-1) + 7亊 (3-1) + 7亊(4-1) + 7亊(5-1) + Sun + Mon + Wed + Wed + Sat
= 70 + 1 + 2 + 4 + 4 + 7
= 88
廬偭偰丄僒僢僇乕傪偡傞擔晅偺悢偺榓偼 88 偲側傞
夝摎丒偦偺14
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
摎偊丗俉俉擔
崱夞偼娙扨偱偡偹丅擔偵偪偑擖傟懼傢偭偰傕摨偠擔悢偩偗壛尭偝傟傞偺偱揔摉偵
擔偵偪傪慖傫偱懌偟偨偺摎偊偱偡丅
傕偆彮偟悢妛揑偵彂偔側傜
丂侾亄俈俙
丂俀亄俈俛
丂係亄俈俠
丂係亄俈俢
丂俈亄俈俤
慡晹懌偡偲侾俉亄俈乮俙亄俛亄俠亄俢亄俤乯
俙乣俤偼奺侽乣係側偺偱偦偺榓偼侾侽
屘偵俉俉
夝摎丒偦偺15
乮儁儞僱亅儉丗kohji乯
戞1廡偐傜帋崌偺擔傪
丂丂丂a,7+b,14+c,21+d,28+e 1亝a,b,c,d亝7 1亝e亝3
偲偟偰昞偡偲偡傞偲丄{a,b,c,d,e}={1,2,4,4,7} 側偺偱
丂a+7+b+14+c+21+d+28+e
=70+a+b+c+d+e
=70+1+2+4+4+7
=88
夝摎丒偦偺16
乮儁儞僱亅儉丗嶰妏掕婯乯
侾丆俀丆俁丆係丆俆丆俇丆俈 偱丆擔丆寧丆壩丆悈丆栘丆嬥丆搚 傪丆 倂1丆倂2丆倂3丆倂4丆倂5 偱戞侾乣戞俆廃傪昞偡偙偲偵偡傞丅 偡傞偲丆僒僢僇乕傪偡傞俆夞偺擔偺崌寁 俽 偼
丂丂丂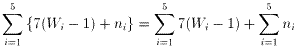 丒丒丒(1)
丒丒丒(1)
偲昞偡偙偲偑偱偒傞偑丆枅廡侾夞偢偮帋崌偡傞偙偲偐傜
丂丂丂丂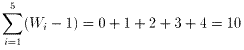 丒丒丒(2)
丒丒丒(2)
傑偨梛擔偺夞悢偺忦審偐傜
丂丂丂丂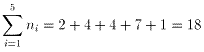 丒丒丒(3)
丒丒丒(3)
(1)(2)(3)傛傝丂俽亖俈亊侾侽亄侾俉亖俉俉丂乧乵摎乶
夝摎丒偦偺17
乮儁儞僱亅儉丗nao乯
傗偭偰傒傟偽偡偖傢偐傞偺偱偡偑丄摎偼俉俉偱偡丅
偳偆偟偰偦偆側傞偺偐丠
擔梛偺悢帤偼侾亄俈亊倎丄寧梛偼俀亄俈亊倐丄悈梛偼係亄俈亊們丄係亄俈亊倓丄搚梛
偼俈亄俈亊倕偲偁傜傢偝傟丄倎丄倐偼侽偐傜係丄們丄倓丄倕偼侽偐傜俁偺偳傟偐偱廳
暋偼偁傝傑偣傫丅
慡晹懌偟偰傑偲傔傞偲丄
丂丂丂侾亄俀亄係亄係亄俈亄俈亊乮倎亄倐亄們亄倓亄倕乯亖侾俉亄俈亊乮侽亄侾亄俀亄俁亄係乯亖侾俉亄俈亊侾侽亖俉俉
偲側傝傑偡丅
偪側傒偵丄壗捠傝峫偊傜傟傞偐偲偄偆偲丄戞俆廡偑擔梛偺応崌侾俀捠傝丄摨偠偔戞俆
廡偑寧梛偺応崌侾俀捠傝偺寁俀係捠傝偁傞偲巚偄傑偡丅
戝曄擄偟偄栤戣偱偟偨丅
夝摎丒偦偺18
乮儁儞僱亅儉丗T_Tatekawa乯
戞5廡偼擔梛擔偐寧梛擔偟偐偁傝傑偣傫偑丄偙偺寁嶼偱偼
偳偺廡偑壗梛擔偐傪峫偊傞昁梫偼偁傝傑偣傫丅
擔梛擔傪婎弨偵峫偊傑偡丅
寧梛擔偼 +1丆悈梛擔偼 +3丆搚梛擔偼 +6丅
擔梛擔偺擔偺崌寁偼
丂丂丂1+8+15+22+29=75
偙偙偵擔梛擔偐傜暯擔丆搚梛擔偵偢傟偨暘偺擔悢傪懌偟傑偡丅
丂丂丂75 + 1 + 3 + 3 + 6 = 88
摎偊偼 88 偱偡丅
夝摎丒偦偺19
乮儁儞僱亅儉丗toshi乯
戞倎廡偺擔梛擔偺擔晅傪幃偱昞偡偲丄
丂丂丂擔丂丗俈倎亅俇
摨條偵丄寧丄悈侾丄悈俀丄搚傪昞偡偲丄
丂丂丂寧丂丗俈倐亅俆
丂丂丂悈侾丗俈們亅俁
丂丂丂悈俀丗俈倓亅俁
丂丂丂搚丂丗俈倕
崌寁偼丄俈乮倎亄倐亄們亄倓亄倕乯亅侾俈
偙偙偱丄枅廡侾夞偢偮帋崌偑偁傞偺偱丄倎丆倐丆們丆倓丆倕偵偼
侾丆俀丆俁丆係丆俆偑奺侾夞偢偮擖傝傑偡丅
偮傑傝丄奺壗廡栚偐偼寛掕偟傑偣傫偑丄乮倎亄倐亄們亄倓亄倕乯偼
昁偢乮侾亄俀亄俁亄係亄俆乯亖侾俆
偲側傝傑偡丅
傛偭偰丄俈亊侾俆亅侾俈亖俉俉
夝摎丒偦偺20
乮儁儞僱亅儉丗than乯
夝摎丗
戞堦廡埲慜偵偼侽擔偺擔悢偑宱偭偰偄偰丄摨條偵戞擇廡埲慜偵偼俈擔丄
戞嶰廡埲慜偵偼侾係擔丄戞巐廡埲慜偵偼俀侾擔丄戞屲廡埲慜偵偼俀俉偺擔悢偑宱偭偰偄傞丅
偦偟偰偙偺寧偼擔梛擔偐傜巒傑偭偰偄傞偺偱丄擔丒寧丒壩丒丒丒偺弴偵侾乣俈傑偱斣崋傪怳傞丅
偙傟偼戞壗廡栚偐偺倃擔栚丄偲偄偆堄枴崌偄偱偁傞丅
偙偙偱丄偨偲偊偽戞堦廡偺壩梛側傜丄
丂丂丂亀侽(戞堦廡埲慜偺擔偵偪)亄俁(壩梛)亖俁擔亁
戞嶰廡偺栘梛側傜丄
丂丂丂亀侾係(戞嶰廡埲慜偺擔偵偪)亄俆(栘梛擔)亖侾俋擔亁
偲偄偆晽偵擔晅偑寁嶼偱偒傞偙偲偑傢偐傞丅
僞僇僔孨偑僒僢僇乕傪偡傞偺偼寧梛擔侾丄悈梛擔俀丄搚梛擔侾丄擔梛擔侾丄
偮傑傝戞壗廡偐偲偼娭學側偟偵丄偁傞廡偺俀擔栚偵侾夞丄偁傞廡偺係擔栚偵俀夞丄
偲偄偭偨嬶崌偵峫偊傞偙偲偑弌棃傞丅
偦偟偰丄偦傟偑廡偵堦夞側偺偩偐傜丄(戞堦廡)丒(戞擇廡)丒丒丒(戞屲廡)偲丄
(寧梛)丒(悈梛俀夞)丒(搚梛)丒(擔梛)傪揔摉偵慻傒崌傢偣傟偽傛偔丄
擔晅偺悢偺榓偼丄偦偺慻傒崌傢偣偵偼埶傜側偄丅
傛偭偰丄
丂丂丂(侽亄俈亄侾係亄俀侾亄俀俉)亄(俀亄係仏俀亄俈亄侾)亖俉俉
傛偭偰丄僞僇僔孨偑偙偺寧偵僒僢僇乕傪偡傞擔晅偺悢偺榓偼俉俉偱偁傞丅
夝摎丒偦偺21
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
寧梛擔偼2亄7亊惍悢丄悈梛擔偼4亄7亊惍悢丄搚梛擔偼7亄7亊惍悢丄擔梛擔偼1亄7亊惍悢偲昞偣傑偡丅
a,b,c,d,e傪惍悢偲偟偰
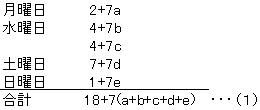
a,b,c,d,e偺屄乆偺抣偼暘偐傝傑偣傫偑丄0,1,2,3,4偺偳傟偐側偺偱
丂丂丂a+b+c+d+e=10 丒丒丒乮俀乯
傛偭偰丄乮侾乯丄乮俀乯傛傝擔晅偺悢偺榓偺崌寁偼丄俉俉擔偱偡丅
夝摎丒偦偺22
乮儁儞僱亅儉丗TORA乯
摎偊丄俉俉擔
亂夁掱(愢柧)亃
壖偵戣堦廡偵慡偰偺楙廗傪峴偆偲偟偰擔悢偺崌寁傪嶼弌丅
丂丂丂侾亄俀亄係亄係亄俈亖侾俉
偳偺梛擔偑戞擇廡乣戞屲廡偵偒偰傕埲壓偺朄懃偼曄傢傜側偄
丂丂丂戞擇廡側傜乧亄俈
丂丂丂戞嶰廡側傜乧亄侾係
丂丂丂戞巐廡側傜乧亄俀侾
丂丂丂戞屲廡側傜乧亄俀俉
廬偭偰偙傟傜傪慡偰偺榓傪媮傔傞偲
丂丂丂侾俉亄俈亄侾係亄俀侾亄俀俉亖俉俉
偵側傞丅
夝摎丒偦偺23
乮儁儞僱亅儉丗岼偺柌乯
捠忢偺楋傪埲壓偺條偵7恑朄偱偁傜傢偡偲丄
| 擔 | 寧 | 壩 | 悈 | 栘 | 嬥 | 搚 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 40 |
| 41 | 42 | 43 | 丂 | 丂 | 丂 |
偙偺楋偐傜擔丄寧丄搚傪奺乆1夞丄偦偟偰悈傪2夞慖傇偺偩偑丄擔媦傃寧埲奜偼4廡偺拞偐傜慖偽偹偽側傜側偄丅
偦偙偱搚梛擔傪悢帤10偲偡傞偲丄懠偼10丄20丄30媦傃40戜偺悢帤偐傜慖傇偟偐側偔丄偙傟傜5悢偺榓偼7恑朄偱140偲側傞丅 堦寘栚偺悢偼4偑2屄丄1偲2偑奺乆1屄偱偁傞偐傜丄7恑朄偱壛偊丄14偲側傞丅 懄偪5悢偺憤榓偼154偱偁傞丅偙傟偼10恑朄偵捈偡偲
丂丂丂1亊72丂+丂5亊7丂+丂4丂亖88
偱偁傞丅 搚梛擔偵20丄30媦傃40傪慖戰偟偰傕忋婰偲慡偔摨條側帠偑惉傝棫偮偺偱丄媮傔傞抣偼88偱偁傞丅
夝摎丒偦偺24
乮儁儞僱亅儉丗Toru乯
夝摎侾
偲傝偁偊偢丄慡晹丄戞侾廡栚偵偟偰寁嶼偡傞偲
丂丂丂1+2+4+4+7=18
俀廡偐傜俆廡栚偺帪偼7,7x2,7x3,7x4 傪偨偡偺偱
偙傟傪偨偟偰丄
丂丂丂18+(7+7x2+7x3+7x4)=18+70=88
夝摎俀
僇儗儞僟乕偺擔晅偗偐傜侾傪堷偄偨傕偺傪俈恑朄偱偁傜傢偡偲
戞侾廡偼0,1,2,--,6丂戞俀廡偼10,11,12,---,16 戞俁廡偼20,21,---,26
戞係廡偼30,31,---,36 戞俆廡偼40,41,42丂偲侾偺埵偺悢偑梛擔傪俈偺埵偺悢偑
戞(n-1)廡栚傪偁傜傢偡
寧侾夞丄悈俀夞丄搚侾夞丄擔侾夞傛傝
丂丂丂侾偺埵偺榓偼1+3+3+6+0=16(7恑朄)
奺廡侾夞偢偮偩偐傜
丂丂丂埵偺榓偼0+10+20+30+40=130(7恑朄)
傛偭偰偙偺榓偼146乮7恑朄乯 侾侽恑朄偵側偍偟偰丄
丂丂丂1x72+4x7+6=83
嵟弶偵堷偄偨侾傪傕偳偟偰俆擔暘偱83+5=88 摎偊
惓夝幰
| 僆儎僕 | teki | 僸儍僋儗儞丒儔儔儞僕儍 |
| 偺偭偙傫 | nao | 僶儖僞儞惎恖 |
| 偙傑偭偨僐 | 僗儌乕僋儅儞 | Toru |
| 忨偺偍偠偝傫 | 揮埵斀墳 | 僥儗僗偲傾儕僗 |
| 岼偺柌 | TORA | than |
| toshi | 傑偡傑偡僞僐偝傫 | 栭傆偐偟偺偮傜偄偍偠偝傫 |
| T_Tatekawa | 儗僀 | 嶰妏掕婯 |
| kohji | 塝搰屲榊 | 俥倎倳倱俿 |
傑偲傔
壗恖偐偺曽偑偟偰偄傞傛偆偵丄忦審偵崌偆傛偆側擔傪慖傫偱寁嶼傪偟偰傒傞偲丄
偳傫側応崌傕昁偢俉俉偵側傞偙偲偑傢偐傝傑偡丅
擔梛擔傪婎弨偵偟偰偄傞曽偑懡偐偭偨傛偆偱偡偑丄
廲偵婎弨傪愝掕偟丄偝傜偵墶偵僗儔僀僪偡傞偲峫偊傟偽偄偄傢偗偱偡偹丅
場傒偵巹帺恎偼恀傫拞偱偁傝丄偐偮俀擔廳側傞悈梛擔傪婎弨偵偟偰丄
丂係亄侾侾亄侾俉亄俀俆亄俁俀亖俋侽
丂偳偙偐偱寧梛擔乮亅俀乯丄偳偙偐偱擔梛擔乮亅俁乯丄偳偙偐偱搚梛擔乮亄俁乯
丂傛偭偰丄俋侽亅俀亅俁亄俁亖俉俉
偲峫偊傑偟偨丅
偙偺峫偊曽傪丄岼偺柌偝傫丄Toru偝傫偑丄
俈恑朄偱惍棟偟偰偔偩偝偄傑偟偨丅俈偺埵偑廡乮僇儗儞僟乕偺廲乯傪昞偟丄侾偺埵偑梛擔乮僇儗儞僟乕偺墶乯
傪昞偟偰偄傞傢偗偱偡丅
傑偨丄TORA偝傫偺夝摎偺儐僯乕僋側偲偙傠偼丄
戞侾廡偵梛擔傪攝抲偟丄偦傟偐傜廡傪妱傝怳傞偲偄偆偙偲偱丄
愭偵墶偺攝抲傪寛傔偰偐傜廲偵妱傝怳傞偲偄偆傕偺偱偡丅
 top
top