Challenge!

問題126　４色カードの問題
Weekend Mathematics／問題／問題126

１２６．４色カードの問題

白、赤、黄、青それぞれ２枚ずつ合計８枚のカードがあります。同じ色には同じ整数が、 違う色には異なる整数が書いてあります。カードに書いてある整数について、次のようなことが わかっています。
　・白２枚と赤１枚に書いてある整数の和は１５です。
　・８枚全部のカードに書いてある整数の和は８０です。
　・赤１枚に書いてある整数の３倍が黄１枚に書いてある整数と等しくなります。
　・白と青のカードのどちらかに整数の１が書いてあります。

(1)　整数の１が書いてあるカードは白、青のどちらですか。

(2)　青１枚、赤２枚、黄１枚のカードに書いてある整数の和を求めなさい。

(3)　何枚かのカードに書いてある整数の和が３５になりました。白、赤、黄、青それぞれの色の枚数を書きなさい。 ただし、使わない色は０枚と書きなさい。

(4)　８枚のうち３枚のカードを取り出すとき、書いてある整数の和は全部でいくつありますか。

問題の出典

センスのよい脳をつくる　大人の算数パズル
河瀬　厚　著
自由国民社
海城中学校　2006年

答えと解説

解答・その1

（ペンネ−ム：やなせ）

ヒント１から赤は奇数でしかも１３以下であることが解る。
　白が１の場合　　　１５−２＝１３
　白が２の場合　　　１５−４＝１１
　　　　・
　　　　・
　　　　・
　白が６の場合　　　１５−１２＝３
　白が７の場合　　　１５−１４＝１
ヒント２から　白＋赤＋黄＋青＝４０
いずれか３種類のカードの合計は最低でも６ですので どの色は別にしても最大数字は ４０−６＝３４以下
ヒント１と２と３から 黄は３．９．１５．２１．２７．３３のいずれか
さらに２と３から 白＋赤＋黄＋青＝黄＋４赤＋青＝４０
４赤は４０−３＝３７以下になるから ３７÷４＝９．２５・・整数だから赤は９以下
これをヒント１に戻すと 白の最小は（１５−９）÷２＝３、 最大は（１５−１）÷２＝７になる
さらにヒント４で白か青、いずれかが１なので 青が１に決定、白は３〜６、赤は３〜９
赤の３倍が黄なので黄は以下のいずれか　９．１５．２１．２７．
これをヒント２に戻し １（青）＋６（白最大）＋９（赤最大）＋？（黄）＝４０になるから 黄は２４以上
黄の候補から２４以上は２７しか無いので黄は２７に決定
さらに黄の１／３が赤なので赤は９に決定
２白＋９（赤）＝１５　　から　白は（１５−９）÷２＝３に決定
青＝１　　白＝３　　赤＝９　　　黄＝２７

問い１の答え　　　　青

問い２の答え　　　　-PASS-

問い３の考え方
青、白、赤をそれぞれ２枚使っても合計は２６　　 これから黄は１枚使用が決定（２枚使うとドボンになる） ３５ー２７＝８　なので赤（９）は使わない これから残りは青と白を２枚づつ使用

問い３の答え　　　　青２枚、白２枚、赤０枚、黄１枚

問い４の答え（ぶっちゃけ虱潰し）
　　５・７・１１・１３・１５・１９・２１・２９・３１・３３・３７・３９・４５・５５・５７・６３の１６種類

解答・その2

（ペンネ−ム：ＦａｕｓＴ）

まず、白（ｗ）赤（ｒ）黄（ｙ）青（ｂ）とし、与えられた条件をこれらの文字に置き換えて整理してみよう。

　　　(1)２ｗ＋ｒ＝１５
　　　(2)ｗ＋ｒ＋ｙ＋ｂ＝４０
　　　(3)３ｒ＝ｙ
　　　(4)ｗかｂのどちらか一方が１

【　解　答　】

１．ｗ＝１と仮定すると、(1)よりｒ＝１３、(3)よりｙ＝３９となるが、これは(2)に矛盾している。 よって、ｂ＝１

２．ｂ＝１と(1)〜(3)から、ｗ＝３、ｒ＝９、ｙ＝２７が求まる。
よって、青（ｂ）１枚、赤（ｒ）２枚、黄（ｙ）１枚の合計は　４６

３．合計が３５になる組み合わせは、２７＋３＋３＋１＋１のみ。
よって、使用するカードの枚数は、白２枚、赤０枚、黄１枚、青２枚

解答・その3

（ペンネ−ム：真夏のサンタ）

答えだけですみません。
（１）　青
（２）４６
（３）青２　白２　赤０　黄１
（４）１６通り

解答・その4

（ペンネ−ム：スモークマン）

(1) 15 =赤+2*白
　　　=1+2*7・・・黄=3・・・青=29
　　　=3+2*6・・・・9・・・・19
　　　=5+2*5・・同じ5になるのでダメ
　　　=7+2*4・・・・21・・・7・・・同じ7になるのでダメ
　　　=9+2*3・・・・27・・・1
　　　=11+2*2・・・33・・・40を超えるのでダメ
　　　=13+2*1・・・39・・・40を超えるのでダメ
上の中で、白か青が1になるのは、5番目のときで、青が1のとき。

(2)上から、（赤、白、黄、青）＝（9，3，27，1）なので、

　　　1*1+9*2+27*1=46

(3)35＝1022 (3進法）から、
白2枚、赤2枚、黄1枚、青0枚

(4)2222 から、3枚取りだすのだから、 3=2+1+0=1+1+1 なので、

　　　4*3+4C3=12+4=16 種類。

解答・その5

（ペンネ−ム：浦島五郎）

白のカード：Ｗ、赤いカード：Ｒ、黄色カード：Ｙ、青いカード：Ｂ　　とする
条件：4種類の色のカードが2枚づつある　同じ色のカードには同じ整数が、 違う色には異なる整数が書かれている

　　　2*W+R=15, 2(W+R+Y+B)=80, 3*R=Y, 1=either(W, B)

(1)W=1のとき　条件式の１番目は、2*1+R=15→R=13　これを条件式の３番目に当てはめると、 3*13=Y→Y=39となって、条件を満たせない　消去法によりB=1とみなす

未知数が３つとなり、式も3式あるので解が得られる

　　　2*W+R=15---(1)
　　　2(W+R+Y+B)=80---(2)
　　　3*R=Y---(3)
　　　B=1---(4)

(3)よりR=1/3*Y

　　　2*W+1/3*Y =15---(1)
　　　W+1/3*Y +Y=39---(2)

　　　2*W+1/3*Y =15---(1)
　　　W+R+4/3*Y=39---(2)

(2)*2-(1)
　　　7/3* Y＝63
Y＝27　∴Ｗ＝3
(3)---3*R＝27
R＝9
Ｗ＝3 、R＝9、Y＝27、B＝1

(2) B+2*R+Y=1+2*9+27=46

(3) 35＝27+6+2＝Ｙ+2*+Ｗ+2*Ｂ
白いカードが2枚、黄色カードが1枚、青いカードが2枚

(4)8枚4種のカードの中から、3枚を選ぶ それは、1種2枚とほかの種類の1枚
　2*W＆R＝6+9＝15
　2*W＆Y＝6+27＝33
　2*W＆B＝6+1＝7
　2*Ｒ＆Ｗ＝18+3＝21
　2*Ｒ＆Y＝18+27＝45
　2*Ｒ＆B＝18+1＝19
　2*Ｙ＆Ｗ＝54+3＝57
　2*Ｙ＆Ｒ＝54+9＝63
　2*Ｙ＆B＝54+1＝55
　2*Ｂ＆Ｗ＝2+3＝5
　2*Ｂ＆Ｒ＝2+9＝11
　2*Ｂ＆Ｙ＝2+27＝29
それは、3枚とも別々の種類
　W＆Ｒ＆Ｙ＝3+9+27＝39
　W＆Ｒ＆B＝3+9+1＝13
　W＆Ｙ＆B＝3+27+1＝31
　Ｒ＆Ｙ＆B＝９+27+1＝37
したがって、16種類

解答・その6

（ペンネ−ム：のっこん）

白の数字をa, 赤の数字をb, 黄の数字をc, 青の数字をd とする

　　　2a+b=15 ・・・(1)
　　　a+b+c+d=40 ・・・(2)
　　　3b=c ・・・(3)

（１）a=1 とすると(1)よりb=13, よって(3)よりc=39 これは(2)に反する
　　従ってd=1 　つまり１は青
（２）2a+b=15, a+b+c=39, 3b=c よりa=3, b=9, c=27
　　従ってd+2b+c=1+18+27=46
（３）黄を使わないと６枚あわせても２６
　　よって黄を１枚使う
　　35-27=8=3*2+1*2 より白２、赤０、黄１、青２
（４）３進法で考える。１、１０，１００，１０００が各２枚あると考えてよい。
　　(1)色がバラバラの時
　　　和は０１１１，１０１１，１１０１，１１１０の４個
　　(2)同じ色がある時
　　　和は２１００，２０１０，２００１，１２００，０２１０，０２０１
　　　　　１０２０，０１２０，００２１，１００２，０１０２，００１２の１２個
　　　合わせて１６個

解答・その7

（ペンネ−ム：まーや）

与えられた条件を式にする。

　　　(ア)２白＋赤＝15
　　　(イ)２白＋２赤＋２黄＋２青＝80
　　　(ウ)３赤＝黄
　　　(エ)白＝１　または　青＝１

(1)白＝１だと仮定する。
(ア)２白＋赤＝15より、２×１＋赤＝15、∴赤＝13
(ウ)３赤＝黄より、黄＝３×13＝39
(イ)に代入
２白＋２赤＋２黄＋２青＝２×１＋２×13＋２×39＋２青＝106＋２青＞80
となり条件に矛盾する。
よって、白＝１だという仮定は誤り。
１が書いてあるカードは青である。・・・（答え）

(2)青＝１を(イ)に代入。
２白＋２赤＋２黄＋２×１＝80
∴２白＋２赤＋２黄＝78・・・(オ)
(ウ)３赤＝黄を(オ)に代入。
２白＋２赤＋２×３赤＝78
∴２白＋８赤＝78・・・(カ)
(カ)２白＋８赤＝78
(ア)２白＋赤＝15
(カ)−(ア)より、７赤＝63、∴赤＝９
(ウ)３赤＝黄に代入。∴黄＝３×９＝27
(ア)２白＋赤＝15より、２白＋９＝15、∴白＝３
青１枚、赤２枚、黄１枚のカードに書いてある整数の和は、
１＋２×９＋27＝46・・・（答え）

(3)黄(27)以外の６枚(白２枚、赤２枚、青２枚)のカードをすべて足しても、
２×３＋２×９＋２×１＝26　にしかならないので、和が35になるには、黄(27)を必ず１枚使う。
黄(27)＋赤(９)＝36＞35となるので、赤は使えない。
35−黄(27)＝８なので、残りのカード(白２枚、青２枚)で８をつくればよい。
白２枚、青２枚使えば８になる。よって、和が35になるには
白２枚、赤０枚、黄１枚、青２枚使う。・・・（答え）

(4)白(３,３)、赤(９,９)、黄(27,27)、青(１,１）

(i)すべて異なる色で３枚取り出すとき
　３＋９＋27＝39
　３＋９＋１＝13
　３＋27＋１＝31
　９＋27＋１＝37　の４個。

(ii)２枚同じ色、１枚異なる色で計３枚取り出すとき
　３＋３＋９＝15　　　27＋27＋３＝57
　３＋３＋27＝33　　　27＋27＋９＝63
　３＋３＋１＝７　　　27＋27＋１＝55
　９＋９＋３＝21　　　１＋１＋３＝５
　９＋９＋27＝45　　　１＋１＋９＝11
　９＋９＋１＝19　　　１＋１＋27＝29　の12個。

(i)、(ii)より
４＋12＝16(個)・・・（答え）

解答・その8

（ペンネ−ム：テレスとアリス）

【解答】
白、赤、黄、青のカードに書かれている整数を それぞれ、W、R、Y、Bとします。 与えられた条件により以下の式が成り立ちます。

　　　2W　+　R　=　15　・・・　（あ）
　　　2（W　+　R　+　Y　+　B）　=　80　・・・　（い）
　　　3R　=　Y　・・・　（う）
　　　W　=　1　または　B　=　1

（い）と（う）から

　　　2W　+　8R　+　2B　=　80

なので、

　　　1　＜　R　＜　10

となります。 （あ）より、Rは奇数となります。 また　Rが5であれば、Wも5となって条件に合いません。 このことより、 Rは　3、7、9　のいずれかです。 Rが3とすれば、（あ）より、Wは6となり、Bが1となりますが、 （い）に代入すると、

　　　2（6　+　3　+　9　+　1）　=　80

となって等式は成り立ちません。 Rが7とすれば、（あ）より、Wは4となり、Bが1となりますが、 （い）に代入すると、

　　　2（4　+　7　+　21　+　1）　=　80

となってやはり等式は成り立ちません。 Rが9の場合、（あ）より、Wは3となり、Bが1となります。 これを（い）に代入すると、

　　　2（3　+　9　+　27　+　1）　=　80

となって、等式が成り立ちます。
以上より、各色のカードの整数は、 白=3、赤=9、黄=27、青=1　になります。

（1）整数の1が書いてあるカードは、青のカードです。

（2）青１枚、赤２枚、黄１枚のカードに書いてある整数の和は、 1　+　（9　×　2）　+　27　で、46　です。

（3）整数の和が３５の時。
白、赤、青すべて６枚の合計は、

　　　2（3　+　9　+　1）　=　26　

で35以下なので、黄のカード（27）が必ず一枚含まれます。 残りの数は8なので、赤のカード（9）は含まれません。 白のカード（3）二枚と青のカード（1）二枚で合計8です。 よって使用するカードは、 白二枚、赤０枚、黄一枚、青二枚　です。

（4）８枚のうち３枚のカードを取り出すときの組み合わせと、 書いてある整数の和は以下の通りです。
　　　（白、白、赤）　=　3　+　3　+　9　=　15
　　　（白、白、黄）　=　3　+　3　+　27　=　33
　　　（白、白、青）　=　3　+　3　+　1　=　7
　　　（赤、赤、白）　=　9　+　9　+　3　=　21
　　　（赤、赤、黄）　=　9　+　9　+　27　=　45
　　　（赤、赤、青）　=　9　+　9　+　1　=　19
　　　（黄、黄、白）　=　27　+　27　+　3　=　57
　　　（黄、黄、赤）　=　27　+　27　+　9　=　63
　　　（黄、黄、青）　=　27　+　27　+　1　=　55
　　　（青、青、白）　=　1　+　1　+　3　=　5
　　　（青、青、赤）　=　1　+　1　+　9　=　11
　　　（青、青、黄）　=　1　+　1　+　27　=　29
　　　（白、赤、黄）　=　3　+　9　+　27　=　39
　　　（白、赤、青）　=　3　+　9　+　1　=　13
　　　（白、黄、青）　=　3　+　27　+　1　=　31
　　　（赤、黄、青）　=　9　+　27　+　1　=　37
以上の16通りです。

解答・その9

（ペンネ−ム：巷の夢）

　白、赤、青及び黄に書かれている数を各々、W,R,B及びYとし、題意に沿って立式すると、

　　　2W+R　＝15　・・・・・(1)
　　　W+R+B+Y　＝40　・・・・(2)
　　　3R　＝Y　・・・・(3)

WないしBには1という数字が含まれる　・・・・(4)
(1)〜(3)式の関係から問題の条件を加味すると以下の表が出来る。

WRBY
39127

（1） 青である
（2） B+2R+Y　＝46
（3） 以下の一通り

W（3）R（9）B（1）Y（27）
2021

（4）16である

W（3）R（9）B（1）Y（27）合計
21　　15
2　1　7
2　　133
12　　21
　21　19
　2　145
1　2　5
　12　11
　　2129
1　　257
　1　263
　　1255
111　12
1　1131
　11137
11　139

解答・その10

（ペンネ−ム：転位反応）

(1) 整数の１が書いてあるカードを白と仮定すると、 与件から、赤のカードは１３、黄のカードは３９。 しかし、与件から導かれる異なる４枚のカードの整数の和は４０であることと、明らかに矛盾。 よって、整数の１が書いてあるカードは青である。
(2)４色カードの整数を求める。（中学入試問題なので負の整数は考えなくて良い）
白２枚と赤１枚の整数の和が１５であることから、赤は奇数。 明らかに与件に反する整数１の場合を除いて検証を行うと、 赤は９と確定できる。

白赤黄青計
639119
5515126
4721133
3927140
21133147

従って、青１枚、赤２枚、黄１枚のカードに書いてある整数の和は、４６

(3)題意を満たすためには、黄１枚を含むことが必須。
３５＝２７＋８
　　＝２７＋１＋１＋３＋３と分解できるので
白２枚、赤０枚、黄１枚、青２枚

(4)８枚のカードから３枚を取り出すとき、カードの色が 全て異なる場合、同じ色のカードを一組含む場合に 分けて考えれば、重複して数えることは無い。
(1)全て異なる場合：４Ｃ３＝４Ｃ１＝４通り
(2)同じ色のカードを一組含む場合：４×３＝１２通り
よって、整数の和は全部で１６

解答・その11

（ペンネ−ム：杖のおじさん）

答え （１）１は青のカードです。
（２）４６です。
（３）白２枚、赤０枚、黄１枚、青２枚
（４）１６通りあります。

条件１．　　２白＋赤＝１５・　・　・　（１）
条件２．　　白＋赤＋青＋黄＝４０･　・　・　（２）
条件３．　　３赤=黄・　・　･　（３）
条件４．　　白叉は青が１･　･　･　（４）

（１） より白＝（１５―赤）／２　･　･　･　（５）
（３） と（５）を（２）に代入する
（１５―赤）／２＋赤＋青＋３赤＝４０・　・　･　（６）
白か青が１ですが白が１であると（１）式の赤が整数で無くなり成立しません。
従って青＝１･　･　・（７）
（７）を（６）に代入して赤を求める。
１５―赤＋２赤＋１×２＋６赤＝８０
７赤＝６３
赤＝９･　･　･　（８）
（８）を（１）に代入する
２白＋９＝１５
白＝６／２＝３･　･　･　（９）
（７）、（８）、（９）を（２）に代入する
３＋９＋１＋黄＝４０
黄＝２７･　･　･　（１０）

問題１．白か青が１ですが白が１であると（１）式の赤が整数で無くなり成立しません。 従って青です。
問題２．整数の和をXとする
　　　X＝青＋２赤＋黄･　･　・　（１１）
青、赤、黄の数字を代入する
　　　X＝１+２×９＋２７＝４６
問題３．大きな数字から決定します。
　　　A+B+C+D=３５
A＝２７×１枚（黄）とすると、残は３５−２７＝８となる。
B＝３×２枚（白）＝６となる。残は８−６＝２となる。
C=１×２枚（青）＝２となる。赤は０枚使用です。
問題４．４＋４×３＝１６通りあります。

解答・その12

（ペンネ−ム：ヒャクレン・ラランジャ）

(1)　青
(2)　１×１＋９×２＋２７×１＝４６
(3)　白２枚、赤０枚、黄１枚、青２枚
(4)　１６個

考え方：
・白２枚と赤１枚に書いてある整数の和は１５です。
　→白２枚は偶数であるので、赤は奇数であることがわかります。
・８枚全部のカードに書いてある整数の和は８０です。
　→各色１枚ずつ、合計４枚のカードに書いてある整数の和は４０になります。
・赤１枚に書いてある整数の３倍が黄１枚に書いてある整数と等しくなります。
　→赤が１０以上になるときは、黄が３０以上となり、４枚の合計が４０をこえてしまうので、 赤は最大９になります。
・白と青のカードのどちらかに整数の１が書いてあります。
　→もし、白が１だとすると、赤は１３になり、条件に合わないので、青のカードが１になります。

以上の条件より、赤は、３,５,７,９のいずれかになります。
赤が３の場合、黄は９、白は６となり、４枚合計４０になりません。
赤が５の場合、白も５となり、条件に合いません。
赤が７の場合、白が１となり、条件に合いません。
赤が９の場合、黄は２７、白は３となり、４枚合計４０、条件に合致します。

よって、４色が決定します。
白３、赤９、黄２７、青１

また、８枚のうち３枚のカードを取り出すとき、取り出し方は、次の１６通りになります。
（１，１，３）（１，１，９）（１，１，２７）（１，３，３）
（１，３，９）（１，３，２７）（１，９，９）（１,９,２７)
（１，２７，２７）（３，３，９）（３，３，２７）（３，９，９）
（３，９，２７）（３，２７，２７）(９，９，２７）（９，２７，２７）
これらすべては、３つの数の和が異なります。

解答・その13

（ペンネ−ム：ますますタコさん）

解答：
（１）青
（２）４６
（３）白２枚、赤０枚、黄１枚、青２枚
（４）１６通り

過程：

（１）白が１だった場合、問題の条件から、「白２枚＋赤＝１５」というのがあり、これから、赤は１３になります。 次に「赤×３＝黄」から黄は３９になります。 そうすると、「白２枚＋赤２枚＋黄２枚＋青２枚＝８０」が「１×２＋１３×２＋３９×２＋･･･」と、 ８０を超えてしまいます。白が１はありえません。
問題に、白と青のどちらかが１とありますから、「青」が１です。

（２）（１）より、青は１です。「白＋赤＋黄＋青」が４０にならないとだめですから、 「白＋赤＋黄」が３９です。「赤×３＝黄」なので、「白＋赤×４」が３９です。 「赤×４」が３７以下にならないといけません（１は青で、同じ数字は使わないので）。 赤は、２〜９の８通りです。（白は「３９−赤−黄」）
　　　「赤＝２、黄＝６、白＝３１」
　　　「赤＝３、黄＝９、白＝２７」
　　　「赤＝４、黄＝１２、白＝２３」
　　　「赤＝５、黄＝１５、白＝１９」
　　　「赤＝６、黄＝１８、白＝１５」
　　　「赤＝７、黄＝２１、白＝１１」
　　　「赤＝８、黄＝２４、白＝７」
　　　「赤＝９、黄＝２７、白＝３」
このなかで、「白２枚＋赤＝１５」を満たすのは、「赤＝９、黄＝２７、白＝３」だけです。 よって、「赤＝９、黄＝２７、白＝３、青＝１」と、カードの色別数字がわかりました。 これより、「青＋赤２枚＋黄」は４６です。

（３）（２）より、これらの数字を２回まで使って和が３５になるのは、 「２７＋２＋２＋１＋１」となります。つまり、「白２枚＋赤０枚＋黄１枚＋青２枚」になります。

（４）４色のカード各２枚、計８枚から、順番に関係なく３枚取り出した時の、 組み合わせは？という問題に置き換えられると思います。
　　　「白、白、赤」「白、白、黄」「白、白、青」（白２枚の時）
　　　「白、赤、赤」「赤、赤、黄」「赤、赤、青」（赤２枚の時）
　　　「白、黄、黄」「赤、黄、黄」「黄、黄、青」（黄２枚の時）
　　　「白、青、青」「赤、青、青」「黄、青、青」（青２枚の時）
　　　「白、赤、黄」「白、赤、青」「白、黄、青」「赤、黄、青」（３枚共違う色の時）
以上、１６通りです。

解答・その14

（ペンネ−ム：T_Tatekawa）

(1) もし白が 1 だとすると，最初の条件から赤が 13 になります．
3番目の条件から黄が 39．
2番目の条件を満たすには，青が -13 でなければなりません．
『整数』だから OK と言えそうですが，(3) が解無しになります．
そこで青が 1 です．

(2) 青が 1 なので，
　　　白＋赤＋黄＝39
です．1番目の条件から，
　　　黄−白＝3×赤−白＝24
となります．また，3番目の条件から，
　　　4×赤＋白＝39
です．両者を組み合わせると，
　　　7×赤＝63 → 赤＝9
です．ここから 黄＝27，白＝3 となります． これらを組み合わせると，
　　　青＋2×赤＋黄＝46
です．

(3) (2) の結果をよく見ると，カードに書かれた数はそれぞれ
　　　1, 3, 3×3, 3×3×3
です．組み合わせて作りたい数があるとき，3 で割って商と余りを 求め，出てきた商をまた 3 で割って商と余りを得るという 操作を繰り返していけば求まります．
　　　35÷3 = 11 あまり 2 → 1 のカードが2枚
　　　11÷3 = 3 あまり 2 → 3 のカードが2枚
　　　3÷3 = 1 あまり 0 → 9 のカードが0枚，27のカードが1枚
よって，
　　　35 = 3×3×3 + 2×3 + 2
です．だから『青2枚，白2枚，赤0枚，黄1枚』です．

(4) 各々のカードは2枚ずつしかないので， 異なるカードの組み合わせで同じ整数の和を作る事は出来ません． 場合分けして考えます．

(a) 同じ色のカードを2枚引く場合．
ある色は2枚引き，別の色のカードは1枚引きます．この場合は

　　　4 × 3 = 12 通り

(b) 3色のカードを1枚ずつ引く場合．
逆に引かないカードの色を選ぶ事になるので，4通り

以上から

　　　12 + 4 = 16 通り．

念のため，出来る値を調べてみると，

　　(a) 5, 7, 11, 15, 19, 21, 29, 33, 45, 55, 57, 63
　　(b) 13, 31, 37, 39

のようです．

解答・その15

（ペンネ−ム：こまったコ）

まず、白のカードをW、赤のカードをR、黄のカードをY、青のカードをBとする。
カードに書いてある整数についてわかっていることをまとめると
　　1) 2W+R=15
　　2) 2(W+R+Y+B)=80　つまり　W+R+Y+B=40
また1)より　15+R+2Y+2B=80 R+2Y+2B=65
　　3) 3R=Y
R+2Y+2B=65　に代入すると 7R+2B=65

(1)の問題では白か青に1が書かれているとあるので
青に1が書かれている場合3)より　7R+2x1=65 R=9
これをR+2Y+2B=65に代入すると　9+2Y+2=65 Y=27
R=9, Y=27　は3)の3R=Y も合致する。

白に1が書かれている場合1)より2x1+R=15, R=13
3)に代入すると　Y=39 になるが、これでは
2)のW+R+Y+B=40が成り立たない。 1+13+39+B=B+53>40
（ただし負の整数まで考えるのであればB=-13で1)〜3)の式が成立する。）

よって、負の整数を考えないと仮定した場合、青(B) に1が書かれているといえる。
また、(1)の問題に「整数の１が書いてある・・・」とあるので
今回の問題では整数＝正の整数を指すと考えられる。

(2)の問題だが、(1)の解答で出したとおり、
B=1より R=9, Y=27 なので　B+2R+Y= 1+2x9+27=46
(また W+9+27+1=40 より　W=3)
(負の整数もありならば -13+2x13+39=52)

(3)の問題は　白、赤、黄、青の各カードの枚数を a,b,c,dとする。
aW+bR+cY+dB=35 つまり3a+9b+27c+d=35。
a,b,c,dは必ず整数であり、またc=2だと式が成り立たないので
3a+9b+27x2+d=35 = 3a+9b+54+d＞35

0≦a≦2、0≦b≦2、0≦c≦1、0≦d≦2の条件付。

まずc=1の場合を考える。
3a+9b+27x1+d=35
3a+9b+d=8　と言うことは　a=2, b=0, d=2 が成り立つ。

次にc=0の場合を考える。
3a+9b+d=35
ここでb=2の場合。
3a+9x2+d=35 つまり　3a+d=17
最高でもa=2, d=2 なので　3x2+2=8 にしかならない。
よってc=0の場合は3a+9b+27c+d=35が成り立たない。

つまり、 白2枚、赤0枚、黄1枚、青2枚。

ここでB=-13の場合も考える。
a+13b+39c-13d=35
0≦a≦2、0≦b≦2、0≦c≦2、0≦d≦2の条件で考える。

まず、d=2の時
a+13b+39c-13x2=35 つまり　a+13b+39c=61　
c=1だとしても　a+13b=22 は上の条件を考えると成り立たないのでこのケースは不成立。
次にd=1の時。
a+13b+39c-13x1=35 つまり　a+13b+39c=48
c=1だとしても　a+13b=9 は上の条件を考えると成り立たないのでこのケースは不成立。

d=0だと必然的にc=0となるがそうなるとa+13b=35上の条件を考えると成り立たない。
ここでやっとB=-13ではないことが判明。
(4) W=3, R=9, Y=27, B=1 なので取り出すカードの組み合わせを考える。
どれかの色を2枚＋他の色1枚の時。

白が2枚＋赤1枚　3x2+9=15
白が2枚＋黄1枚 3x2+27= 33
白が2枚＋青1枚 3x2+1= 7

赤が2枚＋白1枚　9x2+3=21
赤が2枚＋黄1枚　9x2+27=45
赤が2枚＋青1枚　9x2+1=19

黄が2枚＋白1枚　27x2+3=57
黄が2枚＋赤1枚　27x2+9=63
黄が2枚＋青1枚　27x2+1=55

青が2枚+白1枚　1x2+3=5
青が2枚+赤1枚　1x2+9=11
青が2枚+黄1枚　1x2+27=29

3色各1枚ずつの場合

白、赤、黄 3+9+27=39
白、赤、青 3+9+1=13
白、黄、青 3+27+1=31
赤、黄、青 9+27+1=37

5,7,11,13,15,19,21,29,31,33,37,39,46,55,57,63 の16種類。

ということで答えをまとめると。

(1)　青
(2)　46
(3)　白2枚、赤0枚、黄1枚、青2枚
(4)　16通り

解答・その16

（ペンネ−ム：夜ふかしのつらいおじさん）

これは、３進法の問題です。
青の数をｂ、白の数をｗ、赤の数をｒ、黄色の数をｙとします。 分かっていることは、
　　　２ｗ＋ｒ＝１５　・・・　（あ）
　　　２（ｂ＋ｗ＋ｒ＋ｙ）＝８０　つまり　ｂ＋ｗ＋ｒ＋ｙ＝４０　・・・　（い）
　　　３ｒ＝ｙ　・・・　（う）
　　　ｗ＝１　または　ｂ＝１　・・・　（え）

まず、w＝１　としてみます。
すると、（あ）の式より　ｒ＝１３
すると、（う）の式より　ｙ＝３９
すると、（い）の式より　ｂ＝−１３
つまり、青：−１３、白：１、赤：１３、黄：３９です。

次に、ｂ＝１　としてみます。
これと（う）を（い）に代入すると、
ｗ＋４ｒ＝３９　・・・　（お）
（あ）と（お）を連立させると、
ｒ＝９、ｙ＝２７、ｗ＝３
つまり、青：１、白：３、赤：９、黄：２７

(1) この時点では、１が書いてあるカードは、白も青も成立します。

(2) １が白のときは、青１枚、赤２枚、黄１枚の和は、５２
１が青のときは、青１枚、赤２枚、黄１枚の和は、４６

(3) １が白のときは、青２枚、白２枚、赤２枚、黄２枚以内で３５は作れません。
ここの時点で、(1)の問は、青が１となります。

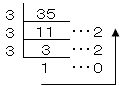１が青のときは、右のように３５を３で次々に割り、商と余りを調べます。
１０進法で３５は、３進法では１０２２と表されます。
だから、青：２、白：２、赤：０、黄：１枚です。

(4)「８枚のうち３枚のカードを取り出すとき、書いてある整数の和は全部でいくつあるか」 という問を、全部で何種類の和ができるかと解釈します。 取り出し方が違えば和の数も異なります。
初めに各色が３枚ずつあったとして、４個の中から３個をとる重複組合わせの場合の数を調べ、 そこから３枚とも同じ場合の数（４）を引いて求めます。
　　　4Ｈ3−４
　　＝6Ｃ3-４
　　＝２０−４
　　＝１６

１＋１＋３＝５　３＋３＋１＝７　９＋９＋１＝１９　２７＋２７＋１＝５５　
１＋１＋９＝１１　３＋３＋９＝１５　９＋９＋３＝２１　２７＋２７＋３＝５７　
１＋１＋２７＝２９　３＋３＋２７＝３３　９＋９＋２７＝４５　２７＋２７＋９＝６３　
１＋３＋９＝１３
１＋３＋２７＝３１
１＋９＋２７＝３７
３＋９＋２７＝３９


解答・その17

（ペンネ−ム：オヤジ）

４色のカードに書かれている整数をそれぞれ
白：Ａ　　赤：Ｂ　　黄：Ｃ　　青：Ｄ　　とする。 条件から
　　　Ａ＋Ｂ＋Ｃ＋Ｄ＝４０　・・（１）　
　　　２Ａ＋Ｂ＝１５ ・・（２）　
　　　３Ｂ＝Ｃ　　・・（３）　
　 　　　Ａ＝１　v　Ｄ＝１ ・・（４）
（４）で　Ａ＝１とするとＢ＝１３，Ｃ＝３９となり　（１）と矛盾する。
従って 　Ａ＝３，Ｂ＝９，Ｃ＝２７，Ｄ＝１　となる

（１）整数１となるカードは，　∴　青
（２）青１枚，赤2枚，黄1枚に書いてある整数の和は？
　　　１×Ｄ＋２×Ｂ＋１×Ｃ＝１＋１８＋２７＝４６
（３）全てのカードを利用すると　１〜８０までの自然数をただ一通りに表すことが出来る
３５を１０進法から３進法に直すと分かりやすい
　　　３５（１０）＝１０２２（３）
∴　白（３）は２枚，赤（９）は０枚，黄（２７）は１枚，青（１）は２枚
（４）カ−ド３枚で出来る数は
　　　１：２色３枚 総数は４Ｃ１×３Ｃ１＝ １２通り
　　　２：３色３枚　総数は４Ｃ３＝　４　通り　　
合わせて　
∴　｛５，７，１１，１３，１５，１９，２１，２９，３１，３３，３７， ３９，４５，５５，５７，６３｝ の　１６通り

解答・その18

（ペンネ−ム：バルタン星人）

(1)各１枚の和は４０、白を１とすると赤は１３、黄は３９、青は−１３、 問題文には「正の整数」とは書かれていないが、単に「正」の書き忘れて と考えると、青が１

(2)青が１なら、白＋赤＋黄（＝赤×３）＝３９
赤＝１５−白×２だから白＋６０−白×８＝３９
白＝３、赤＝９、黄＝２７
青＋赤×２＋黄＝４６

(3)各色の枚数は３進法における１，２，３，４桁目に相当、１対１対応する。
３５は３進法では１０２２（２７＋６＋２）
黄が１枚、白２枚、青２枚

(4)３進法で各桁の和が３になる数字を考える。（）は１０進法での表記 １２（５）、２１（８）、１０２（１１）、１１１（１３）、 １２０（１５）、２０１（１９）、２１０（２１）、 １００２（２９）、１０１１（３１）、１０２０（３３）、 １１０１（３７）、１１１０（３９）、１２００（４５）、 ２００１（５５）、２０１０（５７）、２１００（６３） の１６種類

【別解】
３進法での１対１対応より、３枚の組み合わせの和は全て異なる数となる。 故に組み合わせだけ求めればよい。
３色選ぶ方法（１色残す）・・・４種類
２色選ぶ方法（２色の選び方×１色の選び方）４×３＝１２種類
合計１６種類

３枚に限らず、何枚の合計であってもその和は独立（唯一）となることを ３進法でさらりと言いましたが、こんなものでよろしいでしょうか。

解答・その19

（ペンネ−ム：teki）

１　青
（白＝１とすると、赤は条件１から１３ですが、これだと黄＝３９となり、 ８枚の合計が８０を超えてしまいます。
（但し、負の整数を考えると、青＝−１３で成立してしまいます。この意味では、 問題の条件は不正確ですね。））

２　４６
（青＝１、白＝３、赤＝９、黄＝２７　なので、１＋９×２＋２７＝４６　でいいのですが、 ３進法で１２０１＝４６　でもいいですね。）

３　黄１枚、白２枚、青２枚
（これも３進法の問題ですね。３５を３進法で表すと１０２２なので、 黄＝１．赤＝０、白＝２、青＝２　です。）

４　（１，１，３）（１，１，９）（１，１，２７）（１，３，３）（１，３，９） （１，３，２７）（１，９，９）（１，９，２７）（１，２７，２７） （３，３，９）（３，３，２７）（３，９，９）（３，９，２７）（９，９，２７） （９，２７，２７）（３，２７，２７）の合計１６通り。

解答・その20

（ペンネ−ム：nao）

（１）白が１とすると、赤は１５ー１×２＝１３。また、黄は赤の３倍なので１３× ３＝３９。すると、８枚の合計が８０ということと合わなくなる。そこで、１が書い てあるのは青になる。

（２）８枚の合計８０から青２枚分を引くと７８。これは白２枚、赤２枚、黄２枚の 合計。黄２枚は赤６枚分だから、白２枚と赤８枚が７８になる。白２枚と赤１枚は１ ５だったので、７８ー１５＝６３は赤７枚分になる。赤は６３÷７＝９。白は（１５ー ９）÷２＝３。黄は９×３＝２７とわかる。
青１枚、赤２枚、黄１枚は１＋９×２＋２７＝４６。

（３）黄１枚を使わないと３５にはならない。３５ー２７＝８になるのは青２枚白２ 枚のとき。答え：白２赤０黄１青２

（別解）青白赤黄は１、３、９、２７と３の累乗になっている。そこで３５を３進数 であらわすと１０２２となる。これより黄１赤０白２青２とわかる。

（４）２枚が同じ色の場合が３×４＝１２通り。３枚とも違う色の場合は４通り。 答え：１６

解答・その21

（ペンネ−ム：Toru）

(1) 白が1とすると、赤13、黄39となって、総和80に適さず。よって青が1
(2) 条件１、２より赤１枚、黄２枚、青２枚で65、(1)より赤１枚、黄２枚で63、条 件３より赤７枚で63より赤は9=32、よって黄は27=33、白は3 。これは３進法です ね。青１枚、赤２枚、黄１枚では1201を１０進法になおして、1x33+2x32+1=46
(3) 35は３進法では1022よって青２枚、白２枚、赤０枚、黄１枚
(4) ３進法で
　0012,0021,0102,0111,0120,0201,0210,1002,1011,1020,1101,1110,1200,2001,2010 ,2100
の16通り

解答・その22

（ペンネ−ム：三角定規）

カードに書かれている整数は 「０以上の整数」 とします。

（１） 白，赤，黄，青に書かれている数を Ｗ，Ｒ，Ｙ，Ｂ とすると，題意より

　　　２Ｗ＋Ｒ＝１５　　　　　　　…… (1)
　　　２（Ｗ＋Ｒ＋Ｙ＋Ｂ）＝８０ …… (2)
　　　３Ｒ＝Ｙ　　　　　　　　　　　…… (3)
　　　Ｗ＝１　or　Ｂ＝１　　　　 …… (4)

Ｗ＝１ のとき(1)(3)より Ｒ＝１３，Ｙ＝３９
このとき，(2)より Ｂ＝−１３ となり，題意に適さない。

Ｂ＝１ とすると，(2)より　Ｗ＋Ｒ＋Ｙ＝３９　… (5)
(1)(3)(5)を解いて，Ｗ＝３，Ｒ＝９，Ｙ＝２７ … (6)　となり，題意に適す。
よって，整数 １ が書いてあるのは 青いカード …［答］

（２） (6)より，Ｂ＋２Ｒ＋Ｙ＝１＋１８＋２７＝４６ …［答］

（３） 青，白，赤，黄の枚数を ｂ，ｗ，ｒ，ｙ (0≦ｂ，ｗ，ｒ，ｙ≦２）とすると
　　ｂ＋３ｗ＋９ｒ＋２７ｙ＝３５ … (7)
　　ｂ＋３ｗ＋９ｒ≦２＋６＋１８＝２６　だから，(7)より ｙ＝０ にはなれず，ｙ＝１

このとき，ｂ＋３ｗ＋９ｒ＝８　∴ ｒ＝０，ｂ＋３ｗ＝８　∴ ｂ＝２，ｗ＝２
以上よりカードの枚数は，（青，白，赤，黄）＝（２，２，０，１）枚 …[答]

（４） １＝３0，３＝３1，９＝３2，２７＝３3 および　0≦ｂ，ｗ，ｒ，ｙ≦２　だから， それぞれのカードの枚数が異なるとき，書かれている数の総和は全て異なる。
４色から１枚ずつ３まいのカードを取り出す方法は，４通り。
１色から２枚，もう１色から１枚取り出す方法は，４Ｐ２＝１２通り。
以上より，書いてある整数の和は，全部で　１６　…［答］

解答・その23

（ペンネ−ム：kohji）

白、赤、黄、青に書かれている整数をそれぞれw,r,y,bとする。条件より

　　　2w+r=15 …(i)
　　　2(w+r+y+b)=80 …(ii)
　　　y=3r …(iii)
　　　w=1 or b=1

ここで
　　　(i)⇔r=15-2w
(i),(iii)より
　　　 y=45-6w
(i),(ii),(iii)より
　　　 2(w+15-2w+45-6w+b)=80 ⇔b=7w-20
次に
(イ)b=1のとき
　　　w=(1+20)/7=3
　　　r=15-6=9
　　　y=27
これらは互いに異なるので条件を満たす。 よって
　　　(w,r,y,b)=(3,9,27,1)

また(3)の問題文より何枚かのカードの和が35になる。
このときの白、赤、黄、青の枚数をそれぞれa,b,c,dとおくと、
　　　3a+9b+27c+d=35 ⇔3(a+3b+9c)=35-d
上式で左辺は3の倍数なので、右辺も3の倍数。 また d=0,1,2 より d=2 このとき
　　　3(a+3b+9c)=33⇔3(b+3c)=11-a
同様に考えて a=2、このとき
　　　3(b+3c)=11-2⇔3c=3-b
同様に考えて b=0, c=1　 よって、 (a,b,c,d)=(2,0,1,2)

(ロ)w=1のとき
　　　r=15-2=13
　　　y=45-6=39
　　　b=7-20=-13
これらは互いに異なるので条件を満たす。よって
　　　(w,r,y,b)=(1,13,39,-13)
また(3)の問題文より何枚かのカードの和が35になる。 このときの白、赤、黄、青の枚数をそれぞれa,b,c,dとおくと
　　　a+13b+39c-13d=35⇔13(b+3c-d)=35-a
上式で左辺は13の倍数だが、a=0,1,2 のとき右辺は13の倍数とはならないので不適。

(イ),(ロ)より
　　　(w,r,y,b)=(3,9,27,1)

(1) 整数の1が書いてあるカードは青
(2) b+2r+y=1+18+27=46
(3) 白、赤、黄、青はそれぞれ2枚,0枚,1枚,2枚
(4) (w,r,y,b)=(313,2,33,30) なので 求める和は 3p+3q+3rと示せる。
p,q,r は0以上3以下の整数であり、 p=q=r となるのは4通りであることに注意すると、
　　　4H3-4=20-4=16 (通り)
また a≦b≦c,d≦e≦f、3a+3b+3c=3d+3e+3f のとき、
c＜f とすると、 (上式の左辺)≦3f-2+3f-1+3f-1=7*3f-2＜3f＜(上式の右辺) より不適。
同様に考えて、c＞f のときも不適。
よって c=f　このとき 3a+3b=3d+3e
b＜e とすると、 (上式の左辺)≦2*3e-1＜3e＜(上式の右辺) より不適。
同様に考えて b＞e のときも不適。
よって b=e　 このとき 3a=3d より a=d
以上より
　　　3a+3b+3c=3d+3e+3f⇔a=d, b=e, c=f なので16通りの和は全て異なる。
よって求めるものは16通り。

正解者

のっこん 杖のおじさん ヒャクレン・ラランジャ
バルタン星人 nao オヤジ
転位反応 teki スモークマン
こまったコ Toru T_Tatekawa
ますますタコさん 夜ふかしのつらいおじさん テレスとアリス
真夏のサンタ 巷の夢 三角定規
浦島五郎 やなせ ＦａｕｓＴ
kohji まーや

まとめ

カードに書いてある整数について、混乱を招いてしまい、 申し訳ありませんでした。 小学生がこの問題にチャレンジする時は、整数は正のものしか考えないからいいのでしょうが、 一般的に考えるときは、正の整数(自然数)と明記すべきでした。 負の整数や０も考慮してくださった方、どうもありがとうございました。
さて、この問題は最初、連立方程式のようなものかなと思って解き始めますが、 ４枚のカードの書かれた番号が「１，３，９，２７」とわかると、３進法の問題だ！　 ということになりますね。 そうすると、(3)は、３５の３進法表記ですし。 (4)は重複がないことがわかるので、カードが２枚しかないということに気をつけて 数えればいいということになります。

top