�P�Q�S�D�J�[�h�̑召�W
�\�ɂP�C�Q�C�R�C�S�C�T�C�U�̐����������ꂽ�J�[�h���P�����v�U���A
���ɂ��ď��ɒu����Ă��܂��B�`�C�a�C�b�C�c�̂S�l����������P�����A�����ł�
�����ꂽ������������Ȃ��悤�ɃJ�[�h�����܂����B�����āA�S�l���ꂼ�ꂪ�A
�����ȊO�̂R�l�Ɏ����̃J�[�h�̐����������܂����B
����Ƃ��̎��_�ŁA�����̃J�[�h�̐������S�l�̒��ʼn��Ԗڂɑ傫������������l���P�l�������܂����B
�S�l�̃J�[�h�̑g�ݍ��킹�Ƃ��āA�l������ꍇ�����ׂē����Ȃ����B�͗�̂悤��
�����̑g�ݍ��킹�����������ɕ��ׂē����Ȃ����B
�@�@�@�̏������̗�i�Q�C�R�C�S�C�T�j
���̏o�T
�Z���X�̂悢�]������@��l�̎Z���p�Y��
�͐��@���@��
���R������
�h���w�����w�Z�@2005�N
�����Ɖ��
�E����1
�i�y���l�|���F�X���[�N�}���j
�@1234-6543�A1356-6421�A1235-6542
�̃y�A�ł��ˁB
1256=6521 �ł����A����́A2�C5�������邩��_���ł��ˁB
�E����2
�i�y���l�|���F�V�o�l�����j
�i�P�C�Q�C�R�C�S�j�C�i�P�C�Q�C�R�C�T�j
�i�Q�C�S�C�T�C�U�j�C�i�R�C�S�C�T�C�U�j
�ȊO�Ɂ@
�i�P�C�Q�C�S�C�U�j�C�i�P�C�R�C�T�C�U�j
�̂Q�ʂ肪���荇�v�U�ʂ�ƂȂ�܂��B
�E����3
�i�y���l�|���Fteki�j
����
�i�P�Q�R�S�j�i�P�Q�R�T�j�i�P�Q�S�U�j
�i�P�R�T�U�j�i�Q�S�T�U�j�i�R�S�T�U�j
�̂U�ʂ�B
����@��
�J�[�h�̑g�ݍ��킹���P�T�ʂ肵���Ȃ��̂ŁA�P���l���܂����B
�i�P�Q�R�S�j�F�S�̂ݔ��f�\
�i�P�Q�R�T�j�F�T�̂ݔ��f�\
�i�P�Q�R�U�j�F�R�ƂU�����f�\
�i�P�Q�S�U�j�F�S�̂ݔ��f�\
�i�P�Q�S�T�j�F�N�����f�s�\
�i�P�Q�T�U�j�F�Q�ƂT�����f�\
�i�P�R�S�T�j�F�N�����f�s�\
�i�P�R�S�U�j�F�N�����f�s�\
�i�P�R�T�U�j�F�R�̂ݔ��f�\
�i�P�S�T�U�j�F�P�ƂS�����f�\
�i�Q�R�S�T�j�F�N�����f�s�\
�i�Q�R�S�U�j�F�N�����f�s�\
�i�Q�R�T�U�j�F�N�����f�s�\
�i�Q�S�T�U�j�F�Q�̂ݔ��f�\
�i�R�S�T�U�j�F�R�̂ݔ��f�\
�E����4
�i�y���l�|���F�q���N�����E�������W���j
�����F�U�ʂ�
�l�����F
���ׂĂłP�T��ނ����Ȃ��̂ŁA�����グ�A�������ق��������ƍl���܂����B
�������茩�Ȃ��ƁA�ԈႦ���Ⴂ�܂��B
�@�P�F�i1,2,3,4�j���S�̐l���P�ԖڂƂ킩��B(��ӂɂ���)
�@�Q�F�i1,2,3,5�j���T�̐l���P�ԖڂƂ킩��B(��ӂɂ���)
�@�R�F�i1,2,3,6�j���R�̐l���Q�ԖڂƂ킩��A�U�̐l���P�ԖڂƂ킩��B��ӂɂ���Ȃ��B
�@�S�F�i1,2,4,5�j����ӂɂ���Ȃ��B
�@�T�F�i1,2,4,6�j���S�̐l���Q�ԖڂƂ킩��B(��ӂɂ���)�@
�@�U�F�i1,2,5,6�j���Q�̐l���R�ԖڂƂ킩��A�T�̐l���Q�ԖڂƂ킩��B��ӂɂ���Ȃ��B
�@�V�F�i1,3,4,5�j����ӂɂ���Ȃ��B
�@�W�F�i1,3,4,6�j����ӂɂ���Ȃ��B
�@�X�F�i1,3,5,6�j���R�̐l���R�ԖڂƂ킩��B(��ӂɂ���)
�P�O�F�i1,4,5,6�j���S�̐l���R�ԖڂƂ킩��A�P�̐l���S�ԖڂƂ킩��B��ӂɂ���Ȃ��B
�P�P�F�i2,3,4,5�j����ӂɂ���Ȃ��B
�P�Q�F�i2,3,4,6�j����ӂɂ���Ȃ��B
�P�R�F�i2,3,5,6�j����ӂɂ���Ȃ��B
�P�S�F�i2,4,5,6�j���Q�̐l���S�ԖڂƂ킩��B(��ӂɂ���)
�P�T�F�i3,4,5,6�j���R�̐l���S�ԖڂƂ킩��B(��ӂɂ���)
�E����5
�i�y���l�|���F�܂��܂��^�R����j
�F
�@�@�@�P�Q�R�S�@�E�E�E�S�̐l�����킩��
�@�@�@�P�Q�R�T�@�E�E�E�T�̐l�����킩��
�@�@�@�P�Q�S�U�@�E�E�E�S�̐l�����킩��
�@�@�@�P�R�T�U�@�E�E�E�R�̐l�����킩��
�@�@�@�Q�S�T�U�@�E�E�E�Q�̐l�����킩��
�@�@�@�R�S�T�U�@�E�E�E�R�̐l�����킩��@�@�@�̂U�ʂ�
�ߒ��F
�@����͍l������g�ݍ��킹�������o���āA
�S�Ă̑g�ݍ��킹�ɂ��čl���܂����B�ȊO�̑g�ݍ��킹�ɂ���
���L�Ɏ����܂��B
�@�@�@�P�Q�R�U�@�E�E�E�R�ƂU�̐l���킩��
�@�@�@�P�Q�S�T�@�E�E�E������킩��Ȃ�
�@�@�@�P�Q�T�U�@�E�E�E�Q�ƂT�̐l���킩��
�@�@�@�P�R�S�T�@�E�E�E������킩��Ȃ�
�@�@�@�P�R�S�U�@�E�E�E������킩��Ȃ�
�@�@�@�P�S�T�U�@�E�E�E�P�ƂS�̐l���킩��
�@�@�@�Q�R�S�T�@�E�E�E������킩��Ȃ�
�@�@�@�Q�R�S�U�@�E�E�E������킩��Ȃ�
�@�@�@�Q�R�T�U�@�E�E�E������킩��Ȃ�
�@��L�ŁA������킩��Ȃ��Ƃ����̂́A��������Ԗڂɑ傫���J�[�h��
�����Ă��邩�����ł��Ȃ��Ƃ������Ƃł��B
���������Ԗڂɑ傫���J�[�h�������Ă��邩��m��ɂ́A
���̂R�l�������Ă���J�[�h�ȊO�̎c��̃J�[�h�̐������A�����Ă��邱�Ƃ��A
�����ɂȂ�܂��B
���Ɂu�P�l�����v�킩��E�E�E�Ƃ���̂ŁA�Q�l�킩��ꍇ�͉ɓ���܂���ł����B
�E����6
�i�y���l�|���F�����������j
�����̃J�[�h�����Ԗڂɑ傫������������Ƃ������Ƃ́A
�������猩���Ă��Ȃ��R�̐������Ȃ����Ă���i�Q�R�S���j�Ƃ�������(*)�ł���B
�ȉ��A�S�l�������Ȃ������Q���ɂ��ďq�ׂ�B
���j�Q���̍����R�ȏ�̏ꍇ
���̂Ƃ��A(*)�����҂͂��Ȃ��̂ʼn��͂Ȃ��B
��j�Q���̍����Q�̏ꍇ
���̂Ƃ��A�Q���ɋ��܂ꂽ�J�[�h�����҂݂̂�(*)�����̂ő�ӂɉ����B
�́j�Q���̍����P�̏ꍇ
�Q�����P�Q�A�T�U�̂Ƃ��A(*)�����҂��P�l�Ȃ̂ʼn��ł���A
����ȊO�̂Ƃ��A(*)�����҂��Q�l����̂ʼn��łȂ��B
�ȏ���A��ӂ����Q����
�P�Q�A�P�R�A�Q�S�A�R�T�A�S�U�A�T�U
����āA��
�i�R,�S,�T,�U�j�i�Q,�S,�T,�U�j�i�P,�R,�T,�U�j
�i�P,�Q,�S,�U�j�i�P,�Q,�R,�T�j�i�P,�Q,�R,�S�j
�E����7
�i�y���l�|���F0123210�j
���̓����F(2,4,5,6)(3,4,5,6)(1,3,5,6)(1,2,3,4)(1,2,3,5)(1,2,4,6)
�g�ݍ��킹��15�ʂ肠�邪�A�Œ��l���킩��p�^�[���͓����B
(1,2,4,6)�̂悤��1,2,6���킩���Ă���ꍇ�����l��3,4,5���Ƃ������Ƃ��킩��B
(1,2,3,4)�̂悤��1,2,3���킩���Ă���ꍇ�����l��4,5,6���Ƃ������Ƃ��킩��B
�������A��̓�̃p�^�[���������������Ă�����̂ɒ��ӂ���B
(1,4,5,6)(1,2,5,6)(1,2,3,6)(1,2,5,6)����̐�����������ł���B
����ē����̂悤�Ȍ��ʂƂȂ�B
�E����8
�i�y���l�|���F�o���^�����l�j
���̂R�l���i�P�C�Q�C�R�j�i�S�C�T�C�U�j�i�P�C�T�C�U�j�i�P�C�Q�C�U�j�̎�
���ʂ͂킩��܂��B
�i���ʂ��킩��l�Ԃ��ŕ\���j
�i�P�C�Q�C�R�C4�j�i�P�C�Q�C�R�C5�j�i�P�C�Q�C�R�C6�j
�i�P�C2�C�T�C�U�j�i�P�C3�C�T�C�U�j�i�P�C4�C�T�C�U�j
�i�P�C�Q�C3�C�U�j�i�P�C�Q�C4�C�U�j�i�P�C�Q�C5�C�U�j
�i1�C�S�C�T�C�U�j�i2�C�S�C�T�C�U�j�i3�C�S�C�T�C�U�j
���̒��ł��Ԃ�g�ݍ��킹�́A�S�l���Q�l��
���ʂ��킩��̂ŏ�����
�i�P�C�Q�C�R�C�S�j�i�P�C�Q�C�R�C�T�j�i�P�C�R�C�T�C�U�j�i�P�C�Q�C�S�C�U�j�i�Q�C�S�C�T�C�U�j�i�R�C�S�C�T�C�U�j
�̂U�ʂ�
�E����9
�i�y���l�|���FTo the stars�j
�@��������ԑ傫���ƕ�����P�[�X
�@�ˁi1,2,3�j���������Ƃ��̂�
�A������2�Ԗڂɑ傫���ƕ�����P�[�X
�@�ˁi1,2,6�j���������Ƃ��̂�
�B������3�Ԗڂɑ傫���ƕ�����P�[�X
�@�ˁi1,5,6�j���������Ƃ��̂�
�C��������ԏ������ƕ�����P�[�X
�@�ˁi4,5,6�j���������Ƃ��̂�
���̏�������4�l�̃J�[�h�̑g�ݍ��킹�́A
(1,2,3,4)
(1,2,3,5)
(1,2,3,6)
(1,2,4,6)
(1,2,5,6)
(1,3,5,6)
(1,4,5,6)
(2,4,5,6)
(3,4,5,6)
�����Ȃ��B
���̂����A���Ԗڂɑ傫������������l��1�l�����ɂȂ�P�[�X�́A
(1,2,3,4)
(1,2,3,5)
(1,2,4,6)
(1,3,5,6)
(2,4,5,6)
(3,4,5,6)
�ł���B
�E����10
�i�y���l�|���Fkohji�j
(i)4�Ԗڂɑ傫�����̃J�[�h���������l�������̃J�[�h�̐����킩�鎞
(x,4,5,6)�ƂȂ�K�v������B(x=1,2,3)
�搔���ŏ��̐l�ȊO��3�҂̐���(4,5,6)�ȊO�ł���Ɖ��肷��B�����3�҂̐��̂�����3�ȉ��̐�����
�܂�邱�ƂɂȂ邪�Ax��4,5,6�ł��邱�Ƃ��������A�����ŏ��̐l�͎����̃J�[�h�̐����킩��Ȃ���
�Ŗ�������B
�܂�x=1�̂Ƃ��A4�̃J�[�h���������l��3�Ԗڂɑ傫�����Ƃ�������̂ő�ӂɔ�����B��x��1
�ȏォ��(2,4,5,6),(3,4,5,6)
(ii)3�Ԗڂɑ傫�����̃J�[�h���������l�������̃J�[�h�̐����킩�鎞
(i)�Ɠ��l�ɍl���āA(1,x,5,6)�ƂȂ�K�v������B(x=2,3,4)
�܂�x=2�̂Ƃ��A5�̃J�[�h���������l��2�Ԗڂɑ傫�����Ƃ�������̂ő�ӂɔ�����B��x��2
x=4�̂Ƃ��A1�̃J�[�h���������l��4�Ԗڂɑ傫�����Ƃ�������̂ő�ӂɔ�����B��x��4
�ȏォ��(1,3,5,6)
(iii)2�Ԗڂɑ傫�����̃J�[�h���������l�������̃J�[�h�̐����킩�鎞
(i)�Ɠ��l�ɍl���āA(1,2,x,6)�ƂȂ�K�v������B(x=3,4,5)
�܂�x=3�̂Ƃ��A6�̃J�[�h���������l��1�Ԗڂɑ傫�����Ƃ�������̂ő�ӂɔ�����B��x��3
x=5�̂Ƃ��A2�̃J�[�h���������l��3�Ԗڂɑ傫�����Ƃ�������̂ő�ӂɔ�����B��x��5
�ȏォ��(1,2,4,6)
(iv)1�Ԗڂɑ傫�����̃J�[�h���������l�������̃J�[�h�̐����킩�鎞
(i)�Ɠ��l�ɍl���āA(1,2,3,x)���Ȃ�K�v������B(x=4,5,6)
�܂�x=6�̂Ƃ��A3�̃J�[�h���������l��2�Ԗڂɑ傫�����Ƃ�������̂ő�ӂɔ�����B��x��6
�ȏォ��(1,2,3,4),(1,2,3,5)
(i)�`(iv)���
(1,2,3,4),(1,2,3,5),(1,2,4,6),(1,3,5,6),(2,4,5,6),(3,4,5,6)
�E����11
�i�y���l�|���F�̂�����j
�g�ݍ��킹���S���̐����ŕ\�킷���Ƃɂ���
(1) �P�ԑ傫���Ǝv���Ă����̂͑��̂R�l���P�C�Q�C�R�̎�
�@�@�@���P�Q�R�S�C�P�Q�R�T�C�P�Q�R�U
(2) �Q�Ԃ߂ɑ傫���Ǝv���Ă����̂͑��̂R�l���P�C�Q�C�U�̎�
�@�@�@���P�Q�R�U�C�P�Q�S�U�C�P�Q�T�U
(3) �R�Ԃ߂ɑ傫���Ǝv���Ă����̂͑��̂R�l���P�C�T�C�U�̎�
�@�@�@���P�Q�T�U�C�P�R�T�U�C�P�S�T�U
(4)�P�ԏ������Ǝv���Ă����̂͑��̂R�l���S�C�T�C�U�̎�
�@�@�@���P�S�T�U�C�Q�S�T�U�C�R�S�T�U
�P�Q�R�U�ƂP�Q�T�U�ƂP�S�T�U���d������
�d���͉��Ԃ߂ɑ傫������������l���Q�l���邱�Ƃ�����s�K
����āA�P�Q�R�S�C�P�Q�R�T�C�P�Q�S�U�C�P�R�T�U�C�Q�S�T�U�C�R�S�T�U�̂U�ʂ�
�E����12
�i�y���l�|���F�܁[��j
�����̃J�[�h�����Ԗڂɑ傫����������l������͎̂��̂S�̃p�^�[���B
�p�^�[���i�A�j
�@�i�P�C�Q�C�R�C���j�@�@�����S�C�T�C�U
�p�^�[���i�C�j
�@�i�P�C�Q�C���C�U�j�@�@�����R�C�S�C�T
�p�^�[���i�E�j
�@�i�P�C���C�T�C�U�j�@�@�����Q�C�R�C�S
�p�^�[���i�G�j
�@�i���C�S�C�T�C�U�j�@�@�����P�C�Q�C�R
�������A
�@�i�P�C�Q�C�R�C�U�j���p�^�[���i�A�j�Ɓi�C�j�̏d��
�@�i�P�C�Q�C�T�C�U�j���p�^�[���i�C�j�Ɓi�E�j�̏d��
�@�i�P�C�S�C�T�C�U�j���p�^�[���i�E�j�Ɓi�G�j�̏d��
�̑g�ݍ��킹�́A
�����̃J�[�h�����Ԗڂɑ傫����
������l���Q�l����̂ŁA���̏����ɍ���Ȃ��B
����āA
�����̃J�[�h�����Ԗڂɑ傫����
������l���u�P�l�����v����g�ݍ��킹�́A
�@�i�P�C�Q�C�R�C�S�j�C�i�P�C�Q�C�R�C�T�j
�@�i�P�C�Q�C�S�C�U�j�C�i�P�C�R�C�T�C�U�j
�@�i�Q�C�S�C�T�C�U�j�C�i�R�C�S�C�T�C�U�j�@�̂U�ʂ�B
�E����13
�i�y���l�|���F�I���W�j
�ȉ��@���Ԃ�������l���Ƃ���
�i�P�j�P�ԑ傫���ƕ����� �E�E�J�[�h�o�P�C�Q�C�R�p�������鎖���K�v
�@�@�@�o�P�C�Q�C�R�C4�p�� �o�P�C�Q�C�R�C5�p �E�E�E�Q�ʂ�
�@�@���@�o�P�C�Q�C3�C6�p�͂Q�l���召�W��������
�i�Q�j�Q�Ԗڂɑ傫���ƕ�����@�E�E�J�[�h�o�P�C�Q�C�U�p�������鎖���K�v
�@�@�@�o�P�C�Q�C4�C�U�p�@�E�E�E�P�ʂ�
�@�@���@�o�P�C�Q�C3�C6�p�Ɓo�P�C2�C5�C�U�p�͂Q�l���召�W��������
�i�R�j�R�Ԗڂɑ傫���ƕ�����E�E�J�[�h�o�P�C�T�C�U�p�������鎖���K�v
�@�@�@�o�P�C3�C�T�C�U�p�@�E�E�E�P�ʂ�
�@�@���@�o�P�C2�C5�C�U�p�Ɓo1�C4�C�T�C�U�p�͂Q�l���召�W��������
�i�S�j�P�ԏ������ƕ�����@�E�E �J�[�h�o�S�C�T�C�U�p�������鎖���K�v
�@�@�@�o2�C�S�C�T�C�U�p�Ɓo3�C�S�C�T�C�U�p�@�E�E�E�Q�ʂ�
�@�@���@ �o1�C4�C�T�C�U�p�͂Q�l���召�W��������
�i�P�j�A�i�Q�j�C�i�R�j�A�i�S�j���
���@�o�P�C�Q�C�R�C�S�p�C�o�P�C�Q�C�R�C�T�p�C�o�P�C�Q�C�S�C�U�p�C�o�P�C�R�C�T�C�U�p�C�o�Q�C�S�C�T�C�U�p�C�o�R�C�S�C�T�C�U�p�̂U�ʂ�
�E����14
�i�y���l�|���F�e�������s�j
�U���̃J�[�h����Q����I�ԑg�ݍ��킹�͂P�T�ʂ�B
���̂����A��ӂ����g�ݍ��킹�ɂȂ�̂͂U�ʂ�ŁA���L�̂Ƃ���B
�i�P�C�Q�C�R�C�S�j
�i�P�C�Q�C�R�C�T�j
�i�P�C�Q�C�S�C�U�j
�i�P�C�R�C�T�C�U�j
�i�Q�C�S�C�T�C�U�j
�i�R�C�S�C�T�C�U�j
���Ȃ݂Ɏ��������Ԗڂ��킩��̂͂��ꂼ��ォ��
�S�C�T�C�S�C�R�C�Q�C�R�̃J�[�h���������ҁB
�܂��A�i�P�C�Q�C�S�C�T�j�ȂǂU�ʂ�̑g�ݍ��킹�͒N�����Ԗڂ������炸�A
�c��i�P�C�S�C�T�C�U�j�ȂǂR�ʂ�̑g�ݍ��킹�́u�Q�l�v�����Ԗڂ��������Ă��܂��̂ő�ӂɔ�����B
�E����15
�i�y���l�|���F�ɂ����j
�i�P�j �c��R�l���A�S�C�T�C�U�̏ꍇ �����̃J�[�h���P�C�Q�C�R�̂��Â�ł��A�����͂S�Ԗڂ��Ƃ킩��B --->�i�P�C�S�C�T�C�U�j�A�i�Q�C�S�C�T�C�U�j�A�i�R�C�S�C�T�C�U�j �i�Q�j�c��R�l���A�P�C�Q�C�R�̏ꍇ �����̃J�[�h���S�C�T�C�U�̂��Â�ł��A�����͂P�Ԗڂ��Ƃ킩��B --->�i�P�C�Q�C�R�C�S�j�A�i�P�C�Q�C�R�C�T�j�A�i�P�C�Q�C�R�C�U�j �i�R�j�c��R�l���A�P�C�Q�C�U�̏ꍇ �����̃J�[�h���R�C�S�C�T�̂��Â�ł��A�����͂Q�Ԗڂ��Ƃ킩��B --->�i�P�C�Q�C�R�C�U�j�A�i�P�C�Q�C�S�C�U�j�A�i�P�C�Q�C�T�C�U�j �i�S�j�c��R�l���A�P�C�T�C�U�̏ꍇ �����̃J�[�h���Q�C�R�C�S�̂��Â�ł��A�����͂R�Ԗڂ��Ƃ킩��B --->�i�P�C�Q�C�T�C�U�j�A�i�P�C�R�C�T�C�U�j�A�i�P�C�S�C�T�C�U�j ��L�̂����A�d��������̂́A�P�l�����킩�� �Ƃ�����ӂɔ�����B �]���āA�i�P�C�Q�C�R�C�U�j�A�i�P�C�Q�C�T�C�U�j�͏��O����K�v������B
�i�����j
�i�Q�C�S�C�T�C�U�j�A�i�R�C�S�C�T�C�U�j�A�i�P�C�Q�C�R�C�S�j
�i�P�C�Q�C�R�C�T�j�A�i�P�C�Q�C�S�C�U�j�A�i�P�C�R�C�T�C�U�j�̂U�Ƃ���ł��B
�E����16
�i�y���l�|���F�O�p��K�j
�g�ݍ��킹�̑����́C6�b4��6�b2���P�T �ʂ�B
�i�@�j���̂U�ʂ�̑g�ݍ��킹�̏ꍇ�C�����̐����̏��ʂ��������Ă邱�Ƃ��ł���l�͂��Ȃ��B
�@�@�i�P�C�Q�C�S�C�T�j�C�i�P�C�R�C�S�C�T�j�D�i�P�C�R�C�S�C�U�j�C�i�Q�C�R�C�S�C�T�j
�@�@�i�Q�C�R�C�S�C�U�j�C�i�Q�C�R�C�T�C�U�j
�i�A�j���̂R�ʂ�̏ꍇ�ɂ́C�����̂Q�l���������Ă邱�Ƃ��ł���̂ŕs�K�B
�@�@�i�P�C�Q�C�R�C�U�j�C�i�P�C�S�C�T�C�U�j�C�i�P�C�Q�C�T�C�U�j
�i�B�j���̂U�ʂ�̑g�ݍ��킹�̂Ƃ��C�����̃J�[�h�����l�ЂƂ肾�����C�����̐����̏��ʂ��������Ă邱�Ƃ��ł���B
�@�@�i�P�C�Q�C�R�C�S�j�C�i�P�C�Q�C�R�C�T�j�C�i�P�C�Q�C�S�C�U�j�C�i�P�C�R�C�T�C�U�j
�@�@�i�Q�C�S�C�T�C�U�j�C�i�R�C�S�C�T�C�U�j�@�@�c�m���n
�E����17
�i�y���l�|���F�e���X�ƃA���X�j
�S�l�̃J�[�h�̑g�ݍ��킹�Ƃ��čl������̂́A�P�T�ʂ�ł��B
���ꂼ��ɂ��Č����܂��B
| �i�O�P�j | �i�P�C�Q�C�R�C�S�j | �u�S�v�̃J�[�h�̐l���P�l�����u��������ԑ傫�����v���Ɣ���܂� |
| �i�O�Q�j | �i�P�C�Q�C�R�C�T�j | �u�T�v�̃J�[�h�̐l���P�l�����u��������ԑ傫�����v���Ɣ���܂� |
| �i�O�R�j | �i�P�C�Q�C�R�C�U�j | �u�U�v�̃J�[�h�̐l���u��������ԑ傫�����v���Ɣ���܂����A�u�R�v�̃J�[�h�̐l�́u��������Ԗڂɑ傫�����v���Ɣ���܂� |
| �i�O�S�j | �i�P�C�Q�C�S�C�T�j | �S�l�Ƃ������̐��̈ʒu�����f�ł��܂��� |
| �i�O�T�j | �i�P�C�Q�C�S�C�U�j | �u�S�v�̃J�[�h�̐l���P�l�����u��������Ԗڂɑ傫�����v���Ɣ���܂� |
| �i�O�U�j | �i�P�C�Q�C�T�C�U�j | �u�T�v�̃J�[�h�̐l���u��������Ԗڂɑ傫�����v���Ɣ���܂����A�u�Q�v�̃J�[�h�̐l�́u�������O�Ԗڂɑ傫�����v���Ɣ���܂� |
| �i�O�V�j | �i�P�C�R�C�S�C�T�j | �S�l�Ƃ������̐��̈ʒu�����f�ł��܂��� |
| �i�O�W�j | �i�P�C�R�C�S�C�U�j | �S�l�Ƃ������̐��̈ʒu�����f�ł��܂��� |
| �i�O�X�j | �i�P�C�R�C�T�C�U�j | �u�R�v�̃J�[�h�̐l���P�l�����u�������O�Ԗڂɑ傫�����v���Ɣ���܂� |
| �i�P�O�j | �i�P�C�S�C�T�C�U�j | �u�P�v�̃J�[�h�̐l���u��������ԏ��������v���Ɣ���܂����A�u�S�v�̃J�[�h�̐l�́u�������O�Ԗڂɑ傫�����v���Ɣ���܂� |
| �i�P�P�j | �i�Q�C�R�C�S�C�T�j | �S�l�Ƃ������̐��̈ʒu�����f�ł��܂��� |
| �i�P�Q�j | �i�Q�C�R�C�S�C�U�j | �S�l�Ƃ������̐��̈ʒu�����f�ł��܂��� |
| �i�P�R�j | �i�Q�C�R�C�T�C�U�j | �S�l�Ƃ������̐��̈ʒu�����f�ł��܂��� |
| �i�P�S�j | �i�Q�C�S�C�T�C�U�j | �u�Q�v�̃J�[�h�̐l���P�l�����u��������ԏ��������v���Ɣ���܂� |
| �i�P�T�j | �i�R�C�S�C�T�C�U�j | �u�R�v�̃J�[�h�̐l���P�l�����u��������ԏ��������v���Ɣ���܂� |
�Ƃ������ƂŁA�����̐��̈ʒu���u�P�l�����v���f�ł���̂́A
�@�i�P�C�Q�C�R�C�S�j
�@�i�P�C�Q�C�R�C�T�j
�@�i�P�C�Q�C�S�C�U�j
�@�i�P�C�R�C�T�C�U�j
�@�i�Q�C�S�C�T�C�U�j
�@�i�R�C�S�C�T�C�U�j
�̂U�̑g�ݍ��킹�ł��B
�i�P�C�Q�C�R�C�S�j�Ɓi�R�C�S�C�T�C�U�j�A�i�P�C�Q�C�R�C�T�j�Ɓi�Q�C�S�C�T�C�U�j�A�i�P�C�Q�C�S�C�U�j�Ɓi�P�C�R�C�T�C�U�j�� ���ꂼ�ꗠ�Ԃ��̃p�^�[���ł��B
�E����18
�i�y���l�|���F�J�̖��j
A, B, C, D�̋�ʂȂ�1�`6�̂���4��ނ�I�ԑg�ݍ��킹�� 6C4��15�ł���B
���̂���������ӂ��������l����B
�@�e���p�A1�l������3�l�̐����݂Ď����̐��̑召���������邽�߂ɂ́A
����3�����[�Ɋ���Ă��邱�Ƃ��K�v�ł���B�����A123�Ƃ�456�Ȃ�ǂ��B
���̂Ȃ�A������3�����݂�A������4,5,6�Ȃ���1,2,3�̂ǂꂩ�ł��鎖��������A���Ԃ���������B
���̑��ɂ��邩���l����ƁA126��156�ƕϑ����[3���ł��ǂ����Ƃ�������B
�@�����āA����1���Ă͂߂�ƈȉ��̑g�ݍ��킹���l������B
1234�A1235�A1236�A1456�A2456�A3456�A1246�A1256�A1356�@�Ƃ���ł����̑g�ݍ��킹��
�{����1�l�������������̐��̏��Ԃ�ł��Ȃ����ۂ����l����B
�@����ƁA1456�̏ꍇ�A456���݂�1��������l�͍ŏ����ƕ�����B
�Ɠ�����156���݂�4��������l����Ԗڂɏ������ƕ�����B
����͑�ӂ����Ȃ��B����Ɠ������̂��Ȃ����Ƌᖡ����ƁA1236�A1256���������Ƃ�������B
�@�ȏ��苁�߂�g�ݍ��킹�́i1,2,3,4�j�i1,2,3,5�j�i1,2,4,6�j�i1,3,5,6�j�i2,4,5,6�j�i3,4,5,6�j�̂U�ł���B
�E����19
�i�y���l�|���F�]�ʔ����j
�U���̃J�[�h����S���̃J�[�h��I�ԑg�����́A6�b4=�P�T�ʂ�B
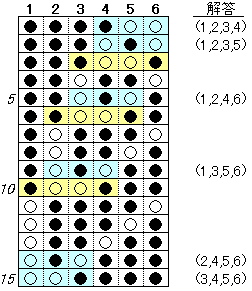
�J�[�h�̕\�����A�������Ƃ��āA�J�[�h�̐������Ƃɐ��������
���\�̒ʂ�B
�����̑g�����̓��A�����̃J�[�h�Ƃ̑召�W���m�肷��
�̂́A�����̃J�[�h�Ɨ��ɂȂ��Ă���Q���̃J�[�h�̎O�̐�
���A������ꍇ�ł���B���\�ɐF�Ŏ������B����āA��ӂ�
�������J�[�h�̑g�����́A���L�̂U�ʂ�ł���B
�Ȃ��A���F�Ŏ������O�̑g�����ł́A�����̏��Ԃ�������
�l����l����B
�E����20
�i�y���l�|���FToru�j
�����̃J�[�h�̐��������Ԗڂɑ傫�����킩�鎞�́A�����ȊO�̂R�l�̐����̑g��
���Ƃ��ẮA (1,2,3) (1,2,6) (1,5,6) (4,5,6)
(1,2,3)�̎��A�����̃J�[�h��4 or 5�Ȃ�OK, 6����3�̐l�ɂ��������Ă��܂��̂ł�
�߁@�����(1,2,3,4) (1,2,3,5)
���l�ɍl���ā@(1,2,6) �̎���4�̂�OK��(1,2,4,6)
(1,5,6)�̎���3�̂�OK��(1,3,5,6)
(4,5,6)�̎���2or 3��OK��(2,4,5,6) (3,4,5,6)
����(1,2,3,4) (1,2,3,5) (1,2,4,6) (1,3,5,6) (2,4,5,6) (3,4,5,6)
�E����21
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
�i�@�P�C�Q�C�R�C�S�@�j�i�@�P�C�Q�C�R�C�T�@�j
�P�C�Q�C�R���������_�Ŏ�������ԑ傫���ƕ�����܂��B
�i�@�Q�C�S�C�T�C�U�@�j�i�@�R�C�S�C�T�C�U�@�j
�S�C�T�C�U���������_�Ŏ�������ԏ������ƕ�����܂��B
�i�@�P�C�Q�C�S�C�U�@�j
�P�C�Q�C�U���������_�Ŏ����͏ォ��Q�Ԗڂł���ƕ�����܂��B
�i�@�P�C�R�C�T�C�U�@�j
�P�C�T�C�U���������_�Ŏ������ォ��R�Ԗڂł���ƕ�����܂��B
�@�@
���������ɓ��莟�̑g�ݍ��킹�������ɊY��������̂�T���܂����B
�@�@�P�C�Q�C�R�C�S�@�@�@�@�P�C�Q�C�R�C�T�@�@�@�P�C�Q�C�R�C�U
�A�@�P�C�S�C�T�C�U�@�@�@�@�Q�C�S�C�T�C�U�@�@�@�R�C�S�C�T�C�U
�B�@�P�C�Q�C�S�C�T�@�@�@�@�P�C�Q�C�S�C�U�@�@�@�P�C�Q�C�T�C�U
�C�@�P�C�R�C�S�C�T�@�@�@�@�P�C�R�C�S�C�U�@�@�@�P�C�R�C�T�C�U
�D�@�Q�C�R�C�S�C�U�@�@�@�@�Q�C�R�C�T�C�U�@�@�@�Q�C�R�C�S�C�T
��L�̑g�ݍ��킹�������Ė��ɂ���u��l���������̏��ʂ�������l������v
�ɊY������g�ݍ��킹��I�т܂����B���̌��ʁA�����Ƃ��ĂU�ʂ�̑g�ݍ��킹��������܂����B
����ȊO�͑��̐l�����������Ԗڂ�����������A�S�������Ԗڂ�������Ȃ��l�����܂��̂ŏ��O���܂����B
�E����22
�i�y���l�|���F��ӂ����̂炢��������j
����������̃J�[�h�����Ĕ��f�ł���ꍇ�������o���܂��B
���ʂ̔ԍ��������������Ă���Ƃ��܂��B
(1)�����̃J�[�h����ԏ������Ɣ��f�ł���ꍇ
(1),4,5,6�@�E�E�E�@�`
(2),4,5,6
(3),4,5,6
(2)�����̃J�[�h����Ԃɏ������Ɣ��f�ł���ꍇ
1,(2),5,6�@�E�E�E�@�a
1,(3),5,6
1,(4),5,6�@�E�E�E�@�`
(3)�����̃J�[�h���O�Ԃɏ������Ɣ��f�ł���ꍇ
1,2,(3),6�@�E�E�E�@�b
1,2,(4),6
1,2,(5),6�@�E�E�E�@�a
(4)�����̃J�[�h����ԑ傫���Ɣ��f�ł���ꍇ
1,2,3,(4)
1,2,3,(5)
1,2,3,(6)�@�E�E�E�@�b
���̂P�Q���݂āA�E�ɃA���t�@�x�b�g���������̂��������̑g�����ɂȂ��Ă��܂��B
�Ⴆ�A�o1,4,5,6�p�̏ꍇ�A
(1)�̐l�͎�������ԏ������ƕ�����A
(4)�̐l�͎�������Ԗڂɏ������ƕ�����܂��B
����ƁA��l�������邱�ƂɂȂ�܂��B
������A�A���t�@�x�b�g�̂��Ă��Ȃ����̂U��ނ����ł��B
(2),4,5,6
(3),4,5,6
1,(3),5,6
1,2,(4),6
1,2,3,(4)
1,2,3,(5)
�E����23
�i�y���l�|���F���܂����R�j
4�l�̍̂�J�[�h4���̑g�ݍ��킹�i�N���ǂ���Ƃ邩�͂��̏ꍇ�W�Ȃ��j��
6C4 = 6C2 = 6x5��2 = 15
(1,2,3,4)�A(1,2,3,5)�A(1,2,3,6)�A(1,2,4,5)�A(1,2,4,6)
(1,2,5,6)�A(1,3,4,5)�A(1,3,4,6)�A(1,3,5,6)�A(1,4,5,6)
(2,3,4,5)�A(2,3,4,6)�A(2,3,5,6)�A(2,4,5,6)�A(3,4,5,6)
��15�ʂ�ł���B
�Ƃ���ŁA�����̎����Ă���J�[�h�̐������킩��Ȃ��Ă�
����3�l�̃J�[�h������Ύ����̃J�[�h�����Ԗڂɑ傫�����������鎞��
����3�l�̃J�[�h�̑g�ݍ��킹���l���Ă݂��B
���̂P
����3�l�̃J�[�h��(1,2,3)�̎��B
�c��̃J�[�h��4,5,6�Ȃ̂łǂ̃J�[�h�������Ă����Ƃ��Ă�
4�l�̒��ň�ԑ傫�������Ƃ������ƂɂȂ�B
����2
����3�l�̃J�[�h��(4,5,6)�̎��B
�c��̃J�[�h��1,2,3�Ȃ̂łǂ̃J�[�h�������Ă����Ƃ��Ă�
4�l�̒��ň�ԏ����������Ƃ������ƂɂȂ�B
����3
����3�l�̃J�[�h��(1,2,6)�̎��A
�c��̃J�[�h��3,4,5�Ȃ̂ŁA�ǂ̃J�[�h�������Ă����Ƃ��Ă�
4�l�̒���2�Ԗڂɑ傫�Ȑ����Ƃ������ƂɂȂ�B
����4
����3�l�̃J�[�h��(1,5,6)�̎��A
�c��̃J�[�h��2,3,4�Ȃ̂ŁA�ǂ̃J�[�h�������Ă����Ƃ��Ă�
4�l�̒���3�Ԗڂɑ傫�Ȑ����Ƃ������ƂɂȂ�B
�Ƃ������Ƃ́A�S15�ʂ�̒���
(1,2,3)�@�{�@�c��̐����̓��P��
(4,5,6)�@�{�@�c��̐����̓��P��
(1,2,6)�@�{�@�c��̐����̓��P��
(1,5,6)�@�{�@�c��̐����̓��P��
�̑g�ݍ��킹�ɂȂ��Ă�����̂������A�Ƃ������ƂɂȂ�B
����1�ɓ��Ă͂܂�̂́A
(1,2,3,4)�A(1,2,3,5)�A(1,2,3,6)��3�ʂ�
���̂Q�ɂ��Ă͂܂�̂́A
(1,4,5,6)�A(2,4,5,6)�A(3,4,5,6)��3�ʂ�
����3�ɓ��Ă͂܂�̂́A
(1,2,3,6)�A(1,2,4,6)�A(1,2,5,6)��3�ʂ�
����4�ɓ��Ă͂܂�̂́A
(1,4,5,6)�A(1,3,5,6)�A(1,2,5,6)��3�ʂ�
���̂����A
(1,2,3,6)�@�i����1�Ƃ���3�ɓ��Ă͂܂�j
(1,4,5,6)�i����2�Ƃ���4�ɓ��Ă͂܂�j
(1,2,5,6)�@�i����3�Ƃ���4�ɓ��Ă͂܂�j
���Ă͂܂�������Q����Ǝ��������Ԗڂɑ傫�������킩��ЂƂ��Q�l���邱�ƂɂȂ�̂ŏ��O����B
3�ʂ�x4�|3�ʂ�~�Q���@6�ʂ�B
(1,2,3,4)�A(1,2,3,5)�A(1,2,4,6)�A(1,3,5,6)�A(2,4,5,6)�A(3,4,5,6)�̂U�ʂ�B
������
�܂Ƃ�
�S�l�̃J�[�h�̑g�ݍ��킹�́A6�b4���P�T �ʂ�ł����A
���̒���������ɍ������̂�T���܂��B���́A�����ȊO�Ɏ����̃J�[�h�̐����������A
���̎��_�Ő����̏��ʂ��킩��Ƃ������̂ł��B
���҂̔��f���܂߂Ĕ��f����Ƃ������Ƃł͂���܂���B
�����ɍ������̂́A�U�ʂ�ɂȂ�܂��B�X�ʂ�Ƃ��������������������܂������A
�i�P�C�Q�C�R�C�U�j�A�i�P�C�Q�C�T�C�U�j�A�i�P�C�S�C�T�C�U�j�͎����̐����̏��ʂ��킩��l���Q�l
����Ƃ������ƂŁA�����ɂ͓K�����܂���B�����̑Ώ̐��ɗ��ӂ���Ɛ����Y�ꂪ����܂���ˁB
 top
top