侾俀俁丏俆偗偨偺惍悢
懢榊偝傫偲壴巕偝傫偺俀恖偑偦傟偧傟丄侾丄俀丄俁丄係丄俆偺俆枃偺僇乕僪傪
暲傋偰俆偗偨偺惍悢傪嶌傝傑偡丅師偺栤偄偵摎偊側偝偄丅
(1) 俀恖偑嶌傞偙偲偺偱偒傞悢偺拞偱丄俆斣栚偵戝偒側悢偼偄偔偮偱偡偐丅
(2) 俀恖偑嶌偭偨悢偺榓傪媮傔偨偲偙傠丄 79482 偲側傝傑偟偨丅
丂丂乮偁乯偙偺寁嶼寢壥偐傜丄俀恖偑嶌偭偨悢偑暘偐傜側偔偰傕丄俀恖偺悢偺榓傪昅嶼偱媮傔傞偲丄
丂丂丂偳偺偗偨傕寁嶼偱傕偔傝忋偑傝偼側偐偭偨偲峫偊傜傟傑偡丅
丂丂丂偦偺棟桼傪娙扨偵愢柧偟側偝偄丅
丂丂乮偄乯俀恖偑嶌偭偨悢傪媮傔側偝偄丅
(3) 俀恖偑嶌偭偨悢偺榓偼 37506 偱偟偨丅俀恖偑嶌偭偨悢傪媮傔側偝偄丅
(4) 俀恖偑嶌偭偨悢偺嵎偼 35820 偱偟偨丅俀恖偑嶌偭偨悢傪媮傔側偝偄丅
栤戣偺弌揟
僙儞僗偺傛偄擼傪偮偔傞丂戝恖偺嶼悢僷僘儖
壨悾丂岤丂挊
帺桼崙柉幮
墶昹櫾梩拞妛崅摍妛峑丂2006擭
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗恀壞偺僒儞僞乯
崱寧偺栤戣偺夝摎傪憲傝傑偡丅摎偊偩偗偱偡偄傑偣傫丅
乮侾乯丂俆係侾俁俀
乮俀乯丂俁係俀俆侾偲係俆俀俁侾
乮俁乯丂侾係俁俆俀偲俀俁侾俆係
乮係乯丂俆侾俀係俁偲侾俆係俀俁
夝摎丒偦偺2
乮儁儞僱亅儉丗僆儎僕乯
乮侾乯俆係侾俁俀
乮俀乯
乮偁乯孞傝忋偑傝偵偼丄忦審偺壓丂俆亄俆丂偑愨懳昁梫偩偑丄昐偺埵偼丄係偱丄
俋偺愮偺埵偺強偱俀悢偼丂俆亄係丂偲側傝丄俆偲係偑堦屄偢偮巊梡偝傟傞丒丒乮A乯
乮俙乯傛傝丄孞傝忋偑傝偼丄婲偙傜側偄丅
傑偨丄8偺廫埵偺強偱傕堦偺埵偼俀偱丄乮A乯偵傛傝乮係亄係乯偼斲掕偝傟傞偺偱丂
俆亄俁丂偲側傞丅丒丒乮B乯
乮A乯丄乮B乯偵傛傝俆偑擇屄暿乆偵巊梡偝傟傞偺偱丂忦審傛傝巆傝係埲壓偺俀屄偺惍悢偺榓偼丄
侾侽枹枮偲側傝孞傝忋偑傝偼丄婲偙傜側偄丅
乮偄乯係俆俀俁侾丂偲丂俁係俀俆侾
丂丂丂丂丂丂丂係俆俀俁侾 丂丂丂丂丂亄丂俁係俀俆侾 丂丂丂丂丂丂丂俈俋係俉俀仸丂孞傝忋偑傝側偟丂偲丂侾乣俆偺悢偑丄俆寘偺悢偵侾夞偢偮尰傟傞帠偱峫偊傞丅
乮俁乯俀俁侾俆係丂偲丂侾係俁俆俀
丂 丂丂丂丂丂俀俁侾俆係 丂丂丂丂亄丂侾係俁俆俀丂 丂丂丂丂丂 丂俁俈俆侽俇仸丂廫偺埵丂俆亄俆丂昐偺埵偺俀悢偺榓偼丄孞傝忋偑傝偺堊丄幚幙丂係
孞傝忋偑傝偼丄廫偺埵偺傒偱丄廫偲昐偺埵埲奜偺懠偺埵偼丄俀悢偺榓丅
屻偼丄侾乣俆偺悢偑丄俆寘偺悢偵侾夞偢偮尰傟傞帠偱峫偊傞丅
乮係乯 俆侾俀係俁丂偲丂侾俆係俀俁
丂丂丂丂丂丂丂俆侾俀係俁
丂丂 丂丂亅丂侾俆係俀俁丂
丂丂 俁俆俉俀侽
仸丂X亜Y偲偟丄X丂亖丂俁俆俉俀侽丂亄丂Y丂丂偱丄
X丂偲Y丂偵侾乣俆偺悢偑丄俆寘偺悢偵侾夞偢偮尰傟傞帠偱峫偊傞丅
夝摎丒偦偺3
乮儁儞僱亅儉丗俥倎倳倱俿乯
乮侾乯丂俆係侾俁俀丂丒丒丒亂夝亃
侾俀侽屄偁傞偆偪偺俆斣栚偲偄偆偙偲偱丄偦偺傑傑悢偊偰偄偒傑偟偨丅
側傫偐堷偭妡偗偱傕偁傞偺偐偲巚偄傑偟偨偑丒丒丒側偄偱偡傛偹乣(^^乁
乮俀乯乮偁乯
亙棟桼亜乽侽乿偑側偄偐傜両
丒丒丒偭偰丄偙偺棟桼偼娙扨偡偓傑偡偹丄偄偔傜側傫偱傕丅
偱偼傕偆彮偟徻偟偔彂偒傑偡丒丒丒俀恖偑巊梡偡傞悢帤偼侾乣俆偺俆偮丅俀恖偺悢帤偺榓偺寁嶼偺嵺偵丄偗偨偑孞傝忋偑傞偺偼偙偺俆偮偺偆偪乽俆亄俆乿偺慻傒崌傢偣丄偡側傢偪俀偮偺悢偺摨偠偗偨偵俆偑偁傞応崌偺傒偱丄偙偺帪丄榓偺悢偵偼乽侽乿偑側偗傟偽側傜側偄丅傑偨丄偙偺乽侽乿偵側傞偗偨偺侾偮塃偺偗偨偼丄巆傞侾乣係偺悢帤偺慻傒崌傢偣偱偼愨懳偵孞傝忋偑傞偙偲偑側偄偨傔丄乽俆亄俆乿偺偗偨偑乽侽乿偱偼側偔乽侾乿傗乽俀乿偵側傞偙偲傕側偄丅
傛偭偰丄乽榓偺悢偵乽侽乿偑側偗傟偽孞傝忋偑傝偼側偄乿偲偄偆偙偲偑尵偊傞偺偩偑丄栤戣偺悢俈俋係俉俀偵偼乽侽乿偑側偄偺偱孞傝忋偑傝偼側偄丄偲尵偊傞丅
乮偄乯丂丂丂俁係俀俆侾
丂丂丂丂亄乯係俆俀俁侾
丂丂丂丂丂丂俈俋係俉俀
傑偢丄榓偺悢偺堦偺埵偺俀偵拲栚丅俀偼侾亄侾偺慻傒崌傢偣偺傒丅
師偵昐偺埵偺係偵拲栚丅係偼侾亄俁偐俀亄俀偩偑丄侾偼婛偵堦偺埵偱俀恖偲傕巊梡偟偰傞偺偱亊丅傛偭偰俀亄俀丅
師偼愮偺埵偺俋丅偙傟傕係亄俆偺慻傒崌傢偣偺傒丅
師偵廫偺埵偺俉丅俉偼俆亄俁偐係亄係偩偑丄愮偺埵偱係傪侾偮巊梡偟偰傞偺偱係亄係偼亊丅傛偭偰俆亄俁丅愮偺埵偱俆傪巊梡偟偰傞傎偆偵偼傕偆俆偑巊梡偱偒側偄偺偱俁傪廩偰丄傕偆堦曽偵俆傪廩偰傞丅
巆傞枩偺埵偵偼巆偭偨俁偲係傪廳暋巊梡偟側偄傛偆偵廩偰傟偽俷俲丅
傛偭偰丄丂丂俁係俀俆侾丂偲丂係俆俀俁侾丂丒丒丒亂夝亃
乮俁乯丂丂丂侾係俁俆俀
丂丂丂丂亄乯俀俁侾俆係
丂丂丂丂丂丂俁俈俆侽俇
傑偢偼枩偺埵偺俁丅僐儗偼侾亄俀偱寛掕丅
師偵丄廫偺埵偺侽偵拲栚偱偡偹丅愭弎乮侾乯乮偁乯偺夝摎偺偲偍傝俆亄俆偺慻傒崌傢偣偟偐偁傝傑偣傫丅
師偵昐偺埵偺俆偵拲栚丅僐僐偱拲堄偡傋偒偼廫偺埵偱偗偨偑孞傝忋偑偭偰偄傞偺傪朰傟側偄偙偲丅
傛偭偰丄懌偟偰俆偱偼側偔丄係偵側傞慻傒崌傢偣傪扵偡丅侾亄俁偐俀亄俀偩偑丄枩偺埵偱俀傪侾偮巊梡偟偰傞偺偱丄俀亄俀偼亊丅傛偭偰侾亄俁丅枩偺埵偱侾傪巊梡偟偰傞傎偆偵偼傕偆侾偑巊梡偱偒側偄偺偱俁傪廩偰丄傕偆堦曽偵侾傪廩偰傞丅
師偼堦偺埵偱傕愮偺埵偱傕丄偳偭偪偐傜傗偭偰傕偄偄偱偡丅巆偭偨悢帤傪廳暋巊梡偟側偄傛偆偵偆傑偔廩偰傟偽俷俲偱偡丅
傛偭偰丄丂丂侾係俁俆俀丂偲丂俀俁侾俆係丂丒丒丒亂夝亃
乮係乯丂丂丂俆侾俀係俁丂丒丒丒懢榊
丂丂丂丂亅乯侾俆係俀俁丂丒丒丒壴巕
丂丂丂丂丂丂俁俆俉俀侽丂丒丒丒嵎
嵟廔栤戣偱堷偒嶼丄偟偐傕孞傝忋偑傝乮孞傝壓偑傝丠乯偑偁偭偰僫僇僫僇庤嫮偄栤戣偱偡偹侓愢柧偟傗偡偄傛偆偵彑庤側偑傜乽懢榊偺悢偐傜壴巕偺悢傪堷偔乿倧倰乽栤戣偺嵎偺悢偵壴巕偺悢傪懌偡偲懢榊偺悢偵側傞乿偲偄偆愝掕偵偟傑偡丅
傑偢偼丄嵎偺悢偺愮偲昐偺埵丄俆偲俉偵拲栚偱偡偐偹丅俀恖偺悢偼侾乣俆偟偐側偄偺偱丄俆偵壴巕偺悢傪懌偡嵺偵侾乣係偱偼懢榊偺悢偑侾乣俆偵側傜側偄偺偱丄壴巕偺愮偺埵偼俆偱寛掕丅俆亄俆亖侽乮侾侽乯偱偡偑丄嵎偺悢偺昐偺埵偑俉偱丄昐偺埵傕孞傝忋偑傝乮丠乯偑惗偠傞偙偲偑柧傜偐偱偡偺偱丄懢榊偺愮偺埵偼侾偵寛掕丅
偙傟傪摜傑偊丄昐偺埵丄嵎亄壴巕亖懢榊丂仺丂俉亄仜亖仮丂傪峫偊傑偡丅仮偼侾侾乣侾俆偵側傜側偗傟偽偄偗側偄偱偡偑丄偙偺偨傔偵偼壴巕偺仜偼俁丒係丒俆偺偄偢傟偐丅偙偙偱丄嵎偺悢偺廫偺埵偲壴巕偺悢偺廫偺埵偺榓偑侾侽埲忋側傜丄仜亖俀傕峫椂偟側偗傟偽側傜側偄偱偡偑丄嵎偺悢偺廫偺埵偑俀偱偁傝丄榓偑侾侽埲忋偵側傞壜擻惈偼側偄偺偱仜亖俀偼峫椂偟側偔偰傛偄偙偲偑妋擣偱偒傑偡丅
偝偰丄仜亖俁丒係丒俆偵娭偟偰偱偡偑丄壴巕偼愮偺埵偱俆傪巊梡偟偰傞偺偱俆偼亊丅俁偩偲俉亄俁亖侾侾偱偡偑丄懢榊偼愮偺埵偱侾傪巊梡偟偰傞偺偱亊丅傛偭偰丄仜亖係偲寛掕丅傑偨丄偝偒傎偳廫偺埵偱偺孞傝忋偑傝偑側偄偙偲傕偁傢偣丄仮亖俀偲寛掕偱偒傑偡丅
師偵堦偺埵偺侽偵拲栚丅嵎偑侽偲偄偆偙偲偼丄懢榊亖壴巕偑柧敀丅偙偙傑偱偱俀恖偑嫟捠偟偰巊梡偟偰側偄偺偼俁偺傒側偺偱俀恖偲傕堦偺埵偼俁偱寛掕丅
師偵廫偺埵丅嵎偑俀偲側傞偺偼俆亅俁丄係亅俀丄俁亅侾偱偡偑丄俁偼堦偺埵偱俀恖偲傕巊偭偰偄傞偺偱懢榊亖係丄壴巕亖俀偑寛掕丅
枩偺埵偼丄偦傟偧傟偺巆傝偺悢帤丄懢榊亖俆丄壴巕亖侾偱丄偙傟偼寁嶼幃傕枮偨偡偺偱俷俲丅
栤戣偱偼懢榊偲壴巕偺戝彫娭學偵偮偄偰偼擟堄偺傛偆側偺偱丄忋婰夝愢偺恖暔愝掕偑媡揮偟偰傕俷俲偱偡偹丅
傛偭偰丄丂丂俆侾俀係俁丂偲丂侾俆係俀俁丂丒丒丒亂夝亃
夝摎丒偦偺4
乮儁儞僱亅儉丗偺偭偙傫乯
乮侾乯丂俆係仜仜仜偲偡傞偲丄仜仜仜偺暲傋曽偼俁両亖俇捠傝
傛偭偰侾丆俀丆俁偺暲傋懼偊偱偱偒傞俁寘偺惍悢偺偆偪
俀斣栚偵彫偝偄悢傪峫偊傟偽傛偄
侾俁俀偑偦傟偵偁偨傞偐傜丄摎偼俆係侾俁俀
乮俀乯偁丏偔傝忋偑傝偼俆亄俆亖侾侽偺帪偺傒婲偙傞
榓偺偳偺寘偵傕侽偼側偄偺偱丄偔傝忋偑傝偼側偐偭偨偙偲偵側傞
偄丏俀悢傪ABCDE丄PQRST偲偡傞丂丂E=T=1丂廬偭偰C=R=2
B=5偲偡傞偲Q=4丂丂偙偺帪D=3丄S=5
A=4丄P=3偲側傞丂丂丂乮摎乯係俆俀俁侾偲俁係俀俆侾
乮俁乯俀悢傪ABCDE丄PQRST偲偡傞丂丂D=S=俆
A=俀偲偡傞偲P=侾丂廬偭偰C=侾丄R=俁
B=俁丄Q=係丂丂E=係丄T=俀偲側傞丂丂丂乮摎乯俀俁侾俆係偲侾係俁俆俀
乮係乯丂戝偒偄曽傪ABCDE丄彫偝偄曽傪PQRST偲偡傞
C亙R丄B亙Q偩偐傜A=俆丄P=侾丂傑偨B=侾丄Q=俆
廬偭偰C=俀丄R=係
D=係丄S=俀丂丂E=T=俁偲側傞丂丂丂乮摎乯俆侾俀係俁偲侾俆係俀俁
夝摎丒偦偺5
乮儁儞僱亅儉丗傑乕傗乯
(1)侾斣戝偒偄悢偼丂54321
俀斣栚偵戝偒側悢偼丂54312
俁斣栚偵戝偒側悢偼丂54231
係斣栚偵戝偒側悢偼丂54213
俆斣栚偵戝偒側悢偼丂54132丂丒丒丒乮摎偊乯
(2)乮偁乯
偔傝忋偑傝偑偁傞偺偼乮俆亄俆乯偺慻傒崌傢偣偺傒丅
俆亄俆亖10側偺偱丄俀恖偑嶌偭偨悢偺榓偵乽侽乿偑娷傑傟傞偲偒偺傒
偔傝忋偑傝偑偁傞丅
栤戣偺乽79482乿偵偼乽侽乿偑娷傑傟側偄偺偱丄偔傝忋偑傝偼側偄丅
乮偄乯
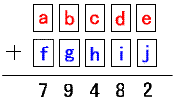
堦偺埵偺榓丄e亄j亖俀偲側傞偺偼丄乮e, j乯亖乮1丆1乯偺傒丅
堦偺埵偱乽侾乿偑偡偱偵巊傢傟偰偄傞偺偱丄昐偺埵乮c, h乯亖乮2丆2乯偱妋掕丅
愮偺埵乮b, g乯亖乮4丆5乯丆乮5丆4乯偺俀捠傝偁傝丄崱偺抜奒偱偼偳偪傜傪慖傫偱傕椙偄偺偱丄
偲傝偁偊偢乮b, g乯亖乮4丆5乯偱妋掕丅
巆偭偨悢帤偐傜峫偊偰
枩偺埵乮a, f乯亖乮3丆4乯丆丂廫偺埵乮d, i乯亖乮5丆3乯偲側傞丅
傛偭偰丄丂34251偲45231丒丒丒乮摎偊乯
(3)
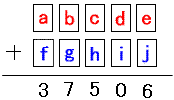
廫偺埵乮d, i乯亖乮5丆5乯偱妋掕丅
枩偺埵乮a, f乯亖乮1丆2乯丆乮2丆1乯偺俀捠傝偁傝丄崱偺抜奒偱偼偳偪傜傪慖傫偱傕椙偄偺偱丄
偲傝偁偊偢乮a, f乯亖乮1丆2乯偱妋掕丅
昐偺埵偵侾偔傝忋偑傞偙偲傪峫偊偰丄乮c, h乯亖乮3丆1乯偱妋掕丅
巆偭偨悢帤偐傜峫偊偰丄
愮偺埵乮b, g乯亖乮4丆3乯丆丂堦偺埵乮e, j乯亖乮2丆4乯偲側傞丅
傛偭偰丄丂14352偲23154丒丒丒乮摎偊乯
(4)
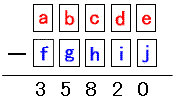
昐偺埵乮c, h乯亖乮1丆3乯丆乮2丆4乯丆乮3丆5乯偺俁捠傝偺偆偪偺偳傟偐偱偁傞丅丒丒丒乮傾乯
愮偺埵偑侾偔傝壓偑傞偙偲傪峫偊偰丄
乮b, g乯亖乮1丆5乯偱妋掕丅丒丒丒乮僀乯
枩偺埵偑侾偔傝壓偑傞偙偲傪峫偊偰丄
乮a, f乯亖乮5丆1乯偱妋掕丅丒丒丒乮僂乯
乮傾乯丄乮僀乯丄乮僂乯偐傜丄
乮c, h乯亖乮2丆4乯偱妋掕丅
巆偭偨悢帤偐傜峫偊偰
廫偺埵乮d, i乯亖乮4丆2乯丆丂堦偺埵乮e, j乯亖乮3丆3乯偲側傞丅
傛偭偰丄丂51243偲15423丒丒丒乮摎偊乯
夝摎丒偦偺6
乮儁儞僱亅儉丗僥儗僗偲傾儕僗乯
亂夝摎亃
乮侾乯侾斣戝偒側悢偼丄乽俆係俁俀侾乿偱偡丅
俀斣栚偼丄乽俆係俁侾俀乿
俁斣栚偼丄乽俆係俀俁侾乿
係斣栚偼丄乽俆係俀侾俁乿
偦偟偰丄丂丂俆斣栚偼丄乽俆係侾俁俀乿丂偱偡丅
乮俀乯乮偁乯
偔傝忋偑傝偑偁傞偺偼乽俆亄俆乿偺帪偩偗偱偁傝丄寁嶼屻偦偺埵偼乽侽乿偲側傝傑偡丅
乽俈俋係俉俀乿偵偼乽侽乿偑娷傑傟偰偄側偄偺偱丄偔傝忋偑傝偼側偐偭偨偲峫偊傜傟傑偡丅
傑偨丄侾亄俀亄俁亄係亄俆亖侾俆丂側偺偱丄
俈亄俋亄係亄俉亄俀亖俁侽丂偲偄偆偙偲偼丄偔傝忋偑傝偼側偐偭偨偙偲偵側傝傑偡丅
傂偲偮偺偔傝忋偑傝偱崌寁偼俋彮側偔側傝傑偡丅
乮偄乯
俀恖偑嶌偭偨悢傪丄ABCDE丂倎倐們倓倕丂偲偟傑偡丅
丂丂丂丂丂丂俙俛俠俢俤 丂丂丂丂亄乯倎倐們倓倕 丂丂丂丂----------------- 丂丂丂丂丂丂俈俋係俉俀俤亖侾丂倕亖侾丂偱偡丅
俠亄們亖係
偔傝忋偑傝偼側偔丄侾亄俁丂偺慻傒崌傢偣偼側偄偺偱丄 俠亖俀丂們亖俀丂偱偡丅
巆傝偺悢偱慻傒崌傢偣傪峫偊傑偡丅
丂丂俙亄倎亖俁亄係亖俈
丂丂俛亄倐亖係亄俆亖俋
丂丂俢亄倓亖俆亄俁亖俉
偲側傝傑偡丅
埲忋偺偙偲偐傜丄俀恖偑嶌偭偨悢偼丄乽俁係俀俆侾乿偲乽係俆俀俁侾乿偲側傝傑偡丅
乮俁乯俀恖偑嶌偭偨悢傪丄ABCDE丂倎倐們倓倕丂偲偟傑偡丅
丂丂丂丂丂丂俙俛俠俢俤 丂丂丂丂亄乯倎倐們倓倕 丂丂丂丂----------------- 丂丂丂丂丂丂俁俈俆侽俇俢亖俆丂倓亖俆丂偱偡丅
俛亄倐亖俈丂偱偡丅
俀亄俆丂偐丂俁亄係丂偑峫偊傜傟傑偡偑丄俆偼巊偊側偄偺偱丄 俁亄係丂偲側傝傑偡丅
E亄倕亖俇丂偱偡丅
俁亄俁丂偐丂係亄俀丂偑峫偊傜傟傑偡偑丄俁偼傂偲偮偟偐巊偊側偄偺偱丄 係亄俀丂偲側傝傑偡丅
俙亄倎亖俁丂偱偡丅
俀亄侾丂偲側傝傑偡丅
俠亄們亖係丂偱偡丂乮偔傝忋偑傝偑偁偭偰俆偵側偭偨乯 侾亄俁丂偲側傝傑偡丅
埲忋偺偙偲偐傜丄俀恖偑嶌偭偨悢偼丄乽侾係俁俆俀乿偲乽俀俁侾俆係乿偲側傝傑偡丅 乮係乯俀恖偑嶌偭偨悢傪丄ABCDE丂倎倐們倓倕丂偲偟傑偡丅
丂丂丂丂丂丂俙俛俠俢俤 丂丂丂丂亅乯倎倐們倓倕 丂丂丂丂----------------- 丂丂丂丂丂丂俁俆俉俀侽愮偺埵偲昐偺埵偑俆埲忋側偺偱丄偦傟偧傟偔傝壓偑傝偑偁偭偨 乮傂偲偮忋偺埵偐傜侾傪庁傝偨乯偲峫偊傜傟傑偡丅
傛偭偰丄俙亖俆丂倎亖侾丂偱偡丅
俢亅倓亖俀丂偱偡丅
俆亅俁丂偐丂係亅俀丂偐丂俁亅侾丂偑峫偊傜傟傑偡偑丄 俢偵俆偼巊偊側偔丄倓偵侾偼巊偊側偄偺偱丄 俢亖係丂倓亖俀丂偱偡丅
俤亅倕亖侽丂偱偡丅
俤亖倕丂側偺偱丄忋婰偱枹巊梡偺悢俁偺傒巊偊傑偡丅
俤亖俁丂倕亖俁丂偱偡丅
巆傝偺悢丂侾丄俀丄係丄俆丂偱丄俛丄倐丄俠丄們丂傪峫偊傑偡丅
俛偲俠偵偼侾偲俀偑丄倐偲們偵偼係偲俆偑丄峫偊傜傟傑偡丅
丂丂丂丂丂丂侾俛俠 丂丂丂丂亅乯丂倐們 丂丂丂丂------------ 丂丂丂丂丂丂丂俆俉偙偺幃偑惉棫偡傞偺偼丄
俛亖侾丂俠亖俀丂倐亖俆丂們亖係丂偺帪偱偡丅
埲忋偺偙偲偐傜丄俀恖偑嶌偭偨悢偼丄乽俆侾俀係俁乿偲乽侾俆係俀俁乿偲側傝傑偡丅
夝摎丒偦偺7
乮儁儞僱亅儉丗偵偟傗傫乯
乮侾乯 戝偒偄弴斣偵暲傋偰偄偔偲
俆亅係亅俁亅俀亅侾
俆亅係亅俁亅侾亅俀
俆亅係亅俀亅俁亅侾
俆亅係亅俀亅侾亅俁
俆亅係亅侾亅俁亅俀
俆亅係亅侾亅俀亅俁
丒
丒
乮摎偊乯 俆係侾俁俀
乮俀乯乮偁乯
偔傝忋偑傝偑偁傞偺偼丄摨偠寘偵俆偑偁傞応崌偩偗偱偁傞丅
偦偺応崌丄偦偺寘偺榓偼僛儘偵側傞丅
俀恖偺榓偺偳偺寘偵傕僛儘偑側偄偨傔丄偔傝忋偑傝偼側偐偭偨偙偲偵側傞丅
乮偄乯
堦偺寘偺榓偑俀側偺偱丄俀恖偺堦偺寘偼丄偦傟偧傟 侾 偱偁傞丅
昐偺寘偺榓偑係側偺偱丄俀恖偺昐偺寘偺慻傒崌傢偣偼丄乮俁丆侾乯傑偨偼乮俀丆俀乯偑峫偊傜傟傞偑丄
偡偱偵 侾 偼巊偭偰偄傞偺偱丄乮俀丆俀乯偱偁傞丅
愮偺寘偺榓偑俋側偺偱丄俀恖偺愮偺寘偺慻傒崌傢偣偼丄乮俆丆係乯偱偁傞丅
枩偺寘偺榓偑俈側偺偱丄俀恖偺枩偺寘偺慻傒崌傢偣偼丄
乮俆丆俀乯傑偨偼乮係丆俁乯偑峫偊傜傟傞偑丄偡偱偵 俀 偼巊偭偰偄傞偺偱丄
乮係丆俁乯偱偁傞丅
廫偺寘偺榓偑俉側偺偱丄俀恖偺廫偺寘偺慻傒崌傢偣偼丄
乮俆丆俁乯傑偨偼乮係丆係乯偑峫偊傜傟傞偑丄
偡偱偵 係偼巊偭偰偄傞偺偱丄乮俆丆俁乯偱偁傞丅
乮摎偊乯 俁係俀俆侾 偲 係俆俀俁侾
乮俁乯
廫偺寘偺榓偑侽側偺偱丄俀恖偺廫偺寘偼丄偦傟偧傟 俆 偱偁傞丅
枩偺寘偺榓偑俁側偺偱丄俀恖偺枩偺寘偺慻傒崌傢偣偼丄乮俀丆侾乯偱偁傞丅
愮偺寘偺榓偑俈側偺偱丄俀恖偺愮偺寘偺慻傒崌傢偣偼丄
乮俆丆俀乯傑偨偼乮係丆俁乯偑峫偊傜傟傞偑丄偡偱偵 俆 偼巊偭偰偄傞偺偱丄
乮係丆俁乯偱偁傞丅
堦偺寘偺榓偑俇側偺偱丄俀恖偺堦偺寘偺慻傒崌傢偣偼丄
乮俆丆侾乯傑偨偼乮係丆俀乯傑偨偼乮俁丆俁乯偑峫偊傜傟傞偑丄
偡偱偵 俆偲俁 偼巊偭偰偄傞偺偱丄乮係丆俀乯偱偁傞丅
昐偺寘偺榓偑俆偱丄侾偔傝忋偑傞偺偱丄俀恖偺昐偺寘偺慻傒崌傢偣偼丄
乮俀丆俀乯傑偨偼乮俁丆侾乯偑峫偊傜傟傞偑丄
偡偱偵 俀 偼巊偭偰偄傞偺偱丄乮俁丆侾乯偱偁傞丅
乮摎偊乯 侾係俁俆俀 偲 俀俁侾俆係
乮係乯
昐偺寘偺嵎偑俉側偺偱丄俀恖偺昐偺寘偼丄乮俀丆係乯傑偨偼乮俁丆俆乯偑峫偊傜傟傞丅
愮偺寘偺嵎偑俆偱丄昐偺寘偵 侾 傪戄偡偺偱丄俀恖偺愮偺寘偼丄乮侾丆俆乯偱偁傞丅
愮偺寘偱 俆 傪巊偭偨偺偱丄俀恖偺昐偺寘偼丄乮俀丆係乯偱偁傞丅
枩偺寘偺嵎偑俁偱丄愮偺寘偵 侾 傪戄偡偺偱丄俀恖偺愮偺寘偼丄乮俆丆侾乯偱偁傞丅
廫偺寘偺嵎偑俀側偺偱丄俀恖偺廫偺寘偼丄乮俆丆俁乯丄乮係丆俀乯丄乮俁丆侾乯偑峫偊傜傟傞偑丄
枩偺寘偱乮俆丆侾乯傪巊偭偰偄傞偺偱丄乮係丆俀乯偱偁傞丅
堦偺寘偺嵎偑侽側偺偱丄俀恖偺堦偺寘偼丄摨偠悢偲側傞偑丄
偡偱偵 侾丆俀丆係丆俆 偼巊偭偰偄傞偺偱丄乮俁丆俁乯偱偁傞丅
乮摎偊乯 俆侾俀係俁 偲 侾俆係俀俁
夝摎丒偦偺8
乮儁儞僱亅儉丗nao乯
乮侾乯戝偒偄弴偵暲傋傞偲丄俆係俁俀侾丄俆係俁侾俀丄俆係俀俁侾丄俆係俀侾俁丄俆
係侾俁俀偲側傞偺偱丄俆斣栚偵戝偒偄偺偼俆係侾俁俀丅
乮俀乯乮偁乯孞傝忋偑傝偑偁傞偺偼丄偦傟偧傟偺摨偠埵偺悢偑俆偲俆偺偲偒偩偗偱丄
偦偺埵偼侽偵側傞丅俈俋係俉俀偵偼侽偑側偄偺偱丄孞傝忋偑傝偼側偐偭偨丅
丂乮偄乯傑偢寛傑傞偺偼侾寘栚偺侾偲侾丅偦偙偱俁寘栚偼俀偲俀偟偐側偔側傞丅師偵丄
係寘栚偼俆偲係偟偐側偄丅偦偙偱丄俀寘栚偼係偲係偑偮偐偊側偄偺偱丄俆偲俁偵側傞丅
嵟屻偵俆寘栚偼俆偑偮偐偊側偄偺偱係偲俁丅
摨偠悢偑偙側偄傛偆偵怳傝暘偗傞偲丄偦傟偧傟丄係俆俀俁侾丄俁係俀俆侾偲側傞丅
乮俁乯俀寘栚偵侽偑偁傞偺偱丄俀寘栚偼偦傟偧傟俆偲俆丅係寘栚偼丄俆偑巊偊側偄偺
偱俁偲係丅侾寘栚偼丄俀偲係丅俁寘栚偼丄侾孞傝忋偑偭偰俆側偺偱懌偟偰係偵側傞侾
偲俁丅嵟屻偺俆寘栚偼丄侾偲俀丅
摨偠悢偑偙側偄傛偆偵怳傝暘偗傞偲丄偦傟偧傟丄侾係俁俆俀丄俀俁侾俆係偵側傞丅
乮係乯侾寘栚偼摨偠悢丅俁寘栚偲係寘栚偵拲栚偡傞偲丄忋偺悢偐傜壓偺悢傪堷偄偰偦
傟偧傟俆偲俉偵側傞偺偼丄偮偓偺埵偐傜庁傝偰偒偨偲偒偩偗偱偁傝丄係寘栚偱俆偵側偭
偰偄傞偺偼侾偲俆偺偲偒偩偲傢偐傞丅乮忋偺侾偼俁寘栚偱堷偔偲偒偵巊偭偰偄傞偺偱
侽偵側傞偐傜乯偡傞偲丄俆寘栚偼俆偲侾偟偐側偄丅俁寘栚偼丄俁乕俆丄俀乕係丄侾乕
俁偺応崌偑峫偊傜傟傞偑丄係寘栚偲俆寘栚偱侾偲俆偑弌暐偭偰偄傞偺偱丄俀偲係偺応
崌偲寛傑傞丅俀寘栚傪係乕俀丄侾寘栚傪俁偲俁偵偡傞偲弌棃忋偑傞丅
丂丂丂俆侾俀係俁乕侾俆係俀俁亖俁俆俉俀侽
摎偊丂俆侾俀係俁偲侾俆係俀俁
夝摎丒偦偺9
乮儁儞僱亅儉丗岼偺柌乯
乮1乯戝偒側弴傪峫偊偨応崌丄忋擇寘偼54偱偁傞偙偲偼帺柧丄偦偙偱壓嶰寘傪峫偊傟偽椙偄丅
1,2媦傃3偱弌棃傞壜擻側悢偼6庬椶偱偁傞丅場偭偰丄5斣栚偵戝偒側悢偲偡傟偽椙偄丅
懄偪丄嵟忋埵偼1偱偁傝師偼2偐3偺偆偪戝偒偄曽偱偁傞偐傜丄3偲側傞丅嵟廔寘偼巆傝偺2偲側傞丅
埲忋傛傝媮傔傞傕偺偼54132偱偁傞丅
乮2乯
乮偁乯悢1乣5偐傜2悢傪慖傃壛偊偨応崌丄寘偑忋偑傞偺偼5+5亖10偟偐側偄丅
偲偙傠偑79482偲偄偆悢偵偼0偑側偄偺偱寘偑孞傝忋偑傞偙偲偼側偄丅
乮偄乯壓堦寘偐傜峫偊偰偄偔偲丄
丂2亖1+1
丂8亖5+3丄4+4丄
丂4亖3+1丄2+2
丂9亖5+4
丂7亖5+2丄4+3
偲側傞丅偙偙偱2偲9偼寛傑傝偱偁傞偐傜丄1,1,4,5埲奜偺悢偺慻傒崌傢偣傪峫偊偰丄8亖5+3偲側傞丅
偡傞偲1偲5偼2夞巊梡偟偰偟傑偭偨偺偱丄7亖4+3偲側傞丅
偙傟傛傝3傕2夞巊梡偟偰偟傑偭偨偺偱丄4亖2+2偲側傞丅
場偭偰丄媮傔傞悢偼34251偲45231偲側傞丅
乮3乯忋婰偲慡偔摨條側峫偊偱峫嶡傪壛偊傞偲丄14352偲23154偲側傞丅
乮4乯堷偒嶼偱偁傝丄寘忋偑傝傗壓偑傝傪峫偊傞昁梫偑偁傞丅
嶰寘栚媦傃巐寘栚偺8偲5偵拲堄偟偰峫嶡傪壛偊丄51243偲15423傪摼傞丅
夝摎丒偦偺10
乮儁儞僱亅儉丗To the stars乯
(1)
1斣傔偵戝偒側悢佀54321
2斣傔偵戝偒側悢佀54312
3斣傔偵戝偒側悢佀54231
4斣傔偵戝偒側悢佀54213
5斣傔偵戝偒側悢佀54132丒丒丒乮摎乯
(2)
(偁)
5埲壓偺悢帤偟偐側偄偺偱丄嵟戝悢偺5偲5偺榓偺働乕僗偱偟偐丄孞傝忋偑傝偼桳傝摼側
偄丅
5+5=10傛傝丄孞傝忋偑傝偑惗偠傞働乕僗偺1偺埵偼0偱偁傞丅
79482偺1偺埵偼0偱偼側偄偐傜丄孞傝忋偑傝偼惗偠偰偄側偄丅
弴偵10偺埵丄100偺埵丄1000偺埵丄10000偺埵傕0偱側偄偙偲偐傜孞傝忋偑傝偼惗偠偰偄
側偄偙偲偑傢偐傞丅
(偄)
1偺埵偑2偲側傞偺偼乮1,1)偺傒丅
10偺埵偑8偲側傞偺偼乮5,3)丒丒丒嘥丄(4,4)丒丒丒嘦偺傒丅
100偺埵偑4偲側傝丄忋婰偵廳暋偟側偄悢帤傪巊偊傞偺偼乮2,2乯偺傒丅
1000偺埵偑9偲側傝丄忋婰偵廳暋偟側偄悢帤傪巊偊傞偺偼(嘥)偺偲偒乮4,5)偺傒丅
10000偺埵偼梋偭偨悢帤傪峫偊傟偽傛偄偐傜丄偙傟傜傪枮偨偡5寘偺悢帤偼丄
45231偲34251丒丒丒乮摎乯
(3)
10偺埵偑0偲側傞偺偼乮5,5乯偺傒丅
10000偺埵偑3偲側傞偺偼乮1,2乯偺傒丅
1000偺埵偑7偲側傝丄忋婰偵廳暋偟側偄悢帤傪巊偊傞偺偼乮3,4乯偺傒丅
100偺埵偑5偵側傞偺偼丄10偺埵偺孞傝忋偑傝傕峫椂偟丄忋婰偵廳暋偟側偄悢帤傪巊偊傞
偺偼乮3,1乯偺傒丅
1偺埵偼梋偭偨悢帤傪峫偊傟偽傛偄偐傜丄偙傟傜傪枮偨偡5寘偺悢帤偼丄
23154偲14352丒丒丒乮摎乯
(4)
1000偺埵偑5偵側傞偺偼乮1,5乯偺傒丅
10000偺埵偑3偵側傞偺偼丄忋婰傛傝乮5,1乯偺傒丅
1偺埵偑0偵側傝丄忋婰偵廳暋偟側偄悢帤傪巊偊傞偺偼乮2,2乯乮3,3乯乮4,4乯偺傒丅
100偺埵偑8偵側傞偺偼丄忋婰偲弴晄摨偱乮3,4乯乮2,4乯乮2,3乯偱偁傞丅
10偺埵梋偭偨悢帤傪峫偊傟偽傛偄偐傜丄偙傟傜傪枮偨偡5寘偺悢帤偼丄
51243偲15423丒丒丒乮摎乯
夝摎丒偦偺11
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
亙夝摎亜
乮侾乯俆係侾俁俀
乮俀乯乮偁乯孞傝忋偑傞偺偼俆亄俆偺帪偺傒丄偙偺帪丄懠偼係亄係埲壓偲孞傝忋偑傞偙偲偼側偄偺偱丄孞傝忋偑傞偲偒偼昁偢侽傪娷傑側偗傟偽
側傜側偄丅侽偼娷傑傟偰偄側偄偺偱孞傝忋偑傝偼柍偟丅
丂乮偄乯俁係俀俆侾偲係俆俀俁侾
乮俁乯侾係俁俆俀丄俀俁侾俆係
乮係乯俆侾俀係俁丄侾俆係俀俁
亙徻嵶側愢柧亜
(1)弴偵俆係俁俀侾丄俆係俁侾俀丄俆係俀俁侾丄俆係俀侾俁丄俆係侾俁俀
(2)俀亖侾亄侾側偺偱係亖俀亄俀丄俈亖俁亄係丄俉亖俁亄俆丄
俋亖係亄俆乮侾丆俀丆係偑巊梡偝傟傞偺偱偙偺慻傒崌傢偣偺傒乯
俈偱俁傪慖傇偲俉偼俆丄俋偼係偲側傝俁係俀俆侾丄憡庤偼係俆俀俁侾
(3)侽亖俆亄俆丄俈亖俁亄係丄俇亖俀亄係丄俆偼孞傝忋偑傝傪庴偗傞偺偱丄
俆乮係乯亖侾亄俁丄俁亖侾亄俀
俁偱侾傪慖傇偲俆偼俁丄俈偼係丄俇偼俀側偺偱侾係俁俆俀丄憡庤偼俀俁侾俆係
(4)俆媦傃俉偼孞傝壓偑傝傪庴偗傞丅俆偲側傞偺偼侾侾亅俆偺傒丅 俁偼孞傝壓偑傞偺偱幚嵺偼係偺嵎偱俆亅侾丄 侾偲俆偑巊傢傟偨偺偱俉偼侾俀亅係丄俀亖係亅俀丄侽亖俁亅俁丄 懄偪俆侾俀係俁亅侾俆係俀俁
夝摎丒偦偺12
乮儁儞僱亅儉丗揮埵斀墳乯
(1)戣堄偺俆寘偺惍悢偺偆偪丄嵟戝偺惍悢偼俆係俁俀侾
壓俀寘偺暲傃懼偊曽偼俀捠傝丄壓俁寘偺暲傃懼偊曽偼俇捠傝側偺偱丄
俆斣栚偵戝偒側惍悢傪媮傔傞偵偼壓俁寘偺暲傃懼偊偑昁梫偲側傞丅
幚嵺偵暲傃懼偊傪峴偆偲丄俆斣栚偺戝偒側悢偼俆係侾俁俀
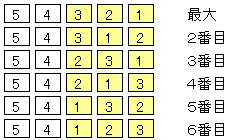
(2)(偁)孞傝忋偑傝偑婲偙傞偺偼丄俆亄俆亖侾侽偺応崌偺傒丅
偙偺俆寘偺惍悢偵丄侽偼娷傑傟偰偄側偄偺偱丄孞傝忋偑傝偼柍偄丅
(偄)俈俋係俉俀偺奺埵偺悢帤傪梌偊傞擇偮偺悢帤偺慡偰偺慻崌偣傪彂偒弌偡丅
慻崌偣偑堦捠傝偩偗偺傕偺偼悢帤偺慻崌偣傪妋掕偱偒傞偺偱丄偦傟傜偺忣曬傪尦偵丄
徚嫀朄偵傛傝惓偟偄慻崌偣傪慖傃丄擇偮偺悢帤傪媮傔傞丅
擇偮偺悢偼俁係俀俆侾偲 係俆俀俁侾
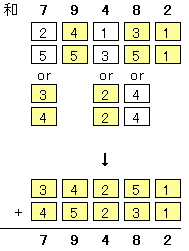
(3)廫埵偼侽側偺偱丄俆亄俆亖侾侽偺悢帤偺慻崌偣偱偁傞丅
傛偭偰丄昐埵傊偺孞傝忋偑傝側偺偱丄
擇偮偺悢帤偺榓偑係偲側傞悢帤偺慻崌偣傪峫偊傟偽椙偄丅
忋婰(偄)偲摨條偵峫偊偰丄媮傔傞悢偼侾係俁俆俀丂偲丂俀俁侾俆係
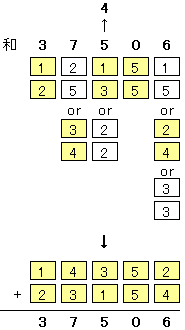
(4)
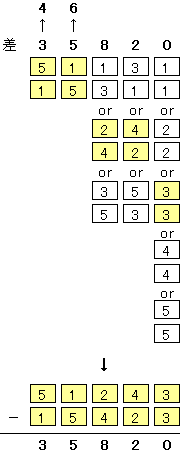
崱搙偼擇偮偺悢偺嵎側偺偱丄奺埵偺悢帤偑俆埲忋偺応崌偵偼孞傝壓偑傝偑婲偙偭偰偄傞丅
廬偭偰丄愮埵偼嵎偑俇丄枩埵偼嵎偑係偺悢帤偺慻崌偣傪峫偊傟偽椙偄丅
摨條偵偟偰丄媮傔傞悢偼俆侾俀係俁丂偲丂侾俆係俀俁
夝摎丒偦偺13
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
(1)54321,54312,54231,54213,54132 側偺偱丄54132 側傫偱偡偹丅(^^;
(2)乮偁乯1,2,3,4,5 偱偔傝偁偑傞偨傔偵偼丄5+5 偟偐側偔丄偦偺帪偼丄0偑偱偒傞偑丄79482
偼丄0傪娷傑側偄偺偱偔傝偁偑偭偰偄傞偼偢偑側偄丅
乮偄乯
7=3+4
9=4+5
4=2+2
8=3+5
2=1+1
偐傜丄34251,45231
(3)
6=2+4
4=1+3
7=3+4
3=1+2
偐傜丄14352,23154
(4)35820 偵懌偟偰54321傛傝彫偝偄堎側傞悢帤偵側傞傕偺傪扵偡偲丄丄丄
15423,51243丂偑枮偨偡偙偲偑暘偐傞丅(^^v
夝摎丒偦偺14
乮儁儞僱亅儉丗kohji乯
(1)
戝偒偄曽偐傜弴偵丄54321,54312,54231,54213,54132
(2)(偁)
孞忋傞偺偼乽俆+俆乿偲寁嶼偡傞帪偺傒偱偁傝丄偦傟偼崅乆1夞偱偁傞丅側偺偱孞傝忋偑傝偑偁偭偨偲偡
傞偲丄嵟崅埵傪彍偔偄偢傟偐偺埵偑0偲側傞堊丅
(偄)
| 1 2 3 4 5 --+---------- 1| 2 3 4 5 6 2| 3 4 5 6 7 3| 4 5 6 7 8 4| 5 6 7 8 9 5| 6 7 8 910(尒偯傜偄偱偡偑2悢偺榓偺昞偱偡丅(^^;)
懢榊丄壴巕偺悢帤偺値寘栚偺惍悢傪偦傟偧傟Tn,Hn偲偡傞丅
孞傝忋偑傜側偄偺偱忋偺昞偐傜
T1=H1=1, T3=H3=2, {T5,H5}={3,4}, {T4,H4}={4,5}, {T2,H2}={3,5}
偟偨偑偭偰師偺傛偆偵側傞丅
丂丂丂{懢榊,壴巕}={34251,45231}
(3)
廫偺埵偱孞傝忋偑傞偙偲偵拲堄偟丄忋偺昞偐傜
T2=H2=5, {T4,H4}={3,4}, {T1,H1}={2,4}, {T5,H5}={1,2}, {T3,H3}={1,3}
偟偨偑偭偰師偺傛偆偵側傞丅
丂丂丂{懢榊,壴巕}={14352,23154}
(4)
{懢榊,壴巕}={10000a+1000b+100c+10d+e,10000A+1000B+100C+10D+E}
({10000a+1000b+100c+10d+e亙10000A+1000B+100C+10D+E})偲偡傞丅 戣堄傛傝丄
丂丂丂10000(a+3)+1000(b+5)+100(c+8)+10(d+2)+(e+0)=10000A+1000B+100C+10D+E
c+8偺堦偺埵偼1乣5側偺偱10
a+3+1偺堦偺埵偼2,3,4,5偱丄4
d+2偺堦偺埵偼3,4偱丄d偼2,3側偺偱 d=2,D=2+2=4
埲忋傛傝e=E=3
偟偨偑偭偰
丂丂丂{懢榊,壴巕}={15423,51243}
夝摎丒偦偺15
乮儁儞僱亅儉丗whale乯
(侾)嶌傞偙偲偺偱偒傞悢帤傪戝偒偄弴偵側傜傋傞偲埲壓偺傛偆偵側傞丅
俆係俁俀侾丄俆係俁侾俀丄俆係俀俁侾丄俆係俀侾俁丄俆係侾俁俀丒丒丒摎偊
(俀)
(偁)孞忋偘偑敪惗偡傞昁梫廫暘忦審偼擇恖偑摨偠寘偵乭俆乭傪抲偔偙偲偱偁傞丅
佁榓偺堦偮偺寘偑乭侽乭偲側傞偙偲偲摨抣偱偁傞丅丒丒丒摎偊
仸傑偨孞傝忋偘偼崅乆堦搙偟偐婲偙傜側偄偙偲偑暘偐傞丅
(偄)堦偺埵偼偍屳偄偵乭侾乭傪慖傫偩偙偲偑暘偐傞丅
忋偲(偁)偺忦審傛傝昐偺埵偼偍屳偄偵乭俀乭偱偁傞丅
偙傟傜偵傛傝枩偺埵偼乷係丆俁乸偺慻傒崌傢偣埲奜偼偁傝偊側偄丅
傑偨愮偺埵傕乷俆丆係乸偺慻傒崌傢偣偟偐側偄丅
廬偭偰廫偺埵偼乷俁丆俆乸偱偁傞丅
屘偵媮傔傞悢偼乷係俆俀俁侾丆俁係俀俆侾乸偺儁傾偱偁傞丅丒丒丒摎偊
(俁)
(偁)傛傝廫偺埵偺寁嶼偵偰孞忋偘偑敪惗偟偨偙偲偑傢偐傞丅
傛偭偰廫偺埵偼乷俆丆俆乸偱偁傞丅
偙傟傜偵傛傝枩偺埵偼乷俀丆侾乸偺慻傒崌傢偣偱偁傞丅(佹懌偟偰乭俁乭偲側傞儁傾傛傝)
昐偺埵偼廫偺埵偱孞忋偘偑敪惗偟偨偨傔懌偟偰乭係乭偲側傞儁傾峫偊傟偽傛偄丅
忋偱偮偐偭偨悢帤傪彍偔偲乷侾丆俁乸偺儁傾偟偐偁傝偊側偄丅
埲忋傛傝愮偺埵丄堦偺埵偺儁傾偼偦傟偧傟乷俁丆係乸乷係丆俀乸偱偁傞丅
屘偵媮傔傞悢偼乷俀俁侾俆係丆侾係俁俆俀乸偺儁傾偱偁傞丅丒丒丒摎偊
(係)
孞傝壓偘寁嶼偑敪惗偡傞昁梫廫暘忦審偼嵎偺寘偑乭俆埲忋乭偱偁傞丅
(佹孞傝壓偘偱堦斣彫偝偄悢帤傪峫偊傞偲侾侾亅俆亖俇丄
俇偺壓偺埵偱孞傝壓偘偑敪惗偟偨偲峫偊傞偲俇亅侾亖俆丄
偲偙傠偱俆偼孞傝壓偘寁嶼柍偟偱偼尰傟側偄)
廬偭偰愮偺埵偲昐偺埵偱偼孞傝壓偘寁嶼偑敪惗偟偰偄傞偙偲偑暘偐傞丅
傛偭偰枩偺埵偼乷俆丆侾乸偺慻傒崌傢偣偟偐側偄丅
愮偺埵偺寛掕偱偁傞偑丄昐偺埵偱孞傝壓偘寁嶼偑婲偒偰偄傞堊丄
嵎偑乭俇乭偲側傞慻傒崌傢偣傪峫偊傟偽傛偄丅傛偭偰乷侾丆俆乸偱偁傞丅
昐偺埵偺慻傒崌傢偣偼嵎偑乭俉乭偲側傞儁傾丅傛偭偰乷俀丆係乸偱偁傞丅
埲忋傛傝廫偺埵丄堦偺埵偺儁傾偼偦傟偧傟乷係丆俀乸乷俁丆俁乸偱偁傞丅
屘偵媮傔傞悢偼乷俆侾俀係俁丆侾俆係俀俁乸偺儁傾偱偁傞丅丒丒丒摎偊
夝摎丒偦偺16
乮儁儞僱亅儉丗嶰妏掕婯乯
乮侾乯 俆係俁俀侾亜俆係俁侾俀亜俆係俀俁侾亜俆係俀侾俁亜俆係侾俁俀 乧乵摎乶
乮俀乯乮偁乯亙棟桼亜孞傝忋偑傝偑偁傞偲偡傟偽丆乽俆亄俆乿丆乽係俆亄俆係亄侾乿 偟偐側偄偑丆
屻幰偼偝傜偵壓偐傜偺孞傝忋偑傝 亄侾 偑側偄偨傔婲偒側偄丅
慜幰偺応崌偵偼孞傝忋偑傝偺偁傞寘偺榓偑 侽 偱側偗傟偽側側偄偑丆
榓偺奺寘偵 侽 偑側偄偨傔孞傝忋偑傝偑側偄丅
丂丂乮偄乯 俁係俀俆侾 亄 係俆俀俁侾 乧乵摎乶
乮俁乯 侾係俁俆俀 亄 俀俁侾俆係 乧乵摎乶
乮係乯 俆侾俀係俁 亅侾俆係俀俁 乧乵摎乶
夝摎丒偦偺17
乮儁儞僱亅儉丗Toru乯
1) 戝偒偄弴偵 54321 54312 54231 54213 54132 偱丂54132
2) (偁) 孞傝忋偑傞偨傔偵偼5+5偑昁梫偱丄偙偺帪偼榓偵侽偑弌偰偔傞偼偢丅
丂丂(偄) 2=1+1, 4=2+2, 7=4+3,8=3+5,9=5+4 偺弴偵侾捠傝偵寛傑偭偰
丂丂丂45231偲34251
3) 10=5+5, 7=3+4, 6=4+2,3=2+1 5=1+3+1 側偳偺弴偵侾捠傝偵寛傔傜傟偰
丂丂丂23154 偲14352
4) 5偺忋偼1-5 丄3偺忋偼5-1丄8偺忋偼2-4 丄0偺忋偼3-3丄丂2偺忋偼4-2丄偺弴偵堦
捠傝偵寛傑傞丅
丂丂丂51243偲15423
夝摎丒偦偺18
乮儁儞僱亅儉丗偙傑偭偨僐乯
(1)偙傟偼慻傒崌傢偣傪侾偮侾偮挷傋偨曽偑憗偄丅
5枃偺僇乕僪偺拞偱傛傝戝偒偄悢傪傛傝忋偺埵偵偟偨曽偑
戝偒側悢偑偱偒傞偙偲傪峫偊傞偲丄5斣栚偵戝偒偄悢偼
丂丂1斣戝偒偄丂5-4-3-2-1丂54321
丂丂2斣戝偒偄丂5-4-3-1-2 54312
丂丂3斣戝偒偄丂5-4-2-3-1 54231
丂丂4斣戝偒偄丂5-4-2-1-3 54213
丂丂5斣戝偒偄丂5-4-1-3-2 54132
傛偭偰 54132丅
(2)(偁)
偙偺庤偺栤戣偑嬯庤側偺偱帺怣偼側偄偑
擇恖偺帩偮僇乕僪偱埵偺悢偺榓偵孞傝忋偑傝偑弌棃偆傞慻傒崌傢偣偼
5+5=10偺傒丅偙偺偲偒丄偦偺埵偵巆傞悢偼0丅
79482偵偼埵偺悢偑0偺埵偑側偄偺偱丄偳偺埵偺寁嶼偱傕
孞傝忋偑傝偼側偐偭偨偲尵偊傞丅
(偄)
懢榊偺嶌偭偨5寘偺悢傪丂ABCDE
壴巕偺嶌偭偨5寘偺悢傪丂VWXYZ 偲偡傞丅
堦偺埵偺悢偺榓偑2偱偁傞偲尵偆偙偲偼丂E+Z=2
偙傟傪枮偨偡E偲Z偺慻傒崌傢偣偼(E,Z) 偲偟偰 (1,1)丅
廫偺埵偺悢偺榓偑8偲偄偆偙偲偼 D+Y=8
堦偺埵偵擇恖偲傕1傪巊偭偨偺偱巆傝偼偦傟偧傟2,3,4,5偱偁傞
偙傟傪枮偨偡D偲Y偺慻傒崌傢偣偼
(D,Y)偲偟偰丂 (3,5), (4,4), (5,3)
昐偺埵偺悢偺榓偑4偲偄偆偙偲偼 C+X=4
堦偺埵偵擇恖偲傕1傪巊偭偨偙偲傪峫偊傞偲
(C,X)偲偟偰丂(2,2)偺傒丅
(1+3=4偺慻傒崌傢偣偑弌棃側偄偺偱)
愮偺埵偺悢偺榓偑9偲偄偆偙偲偼丂B+W=9
偙傟傪枮偨偡B偲W偺慻傒崌傢偣偼
(B,W)偲偟偰丂(4,5), (5,4)丅
偲偄偆偙偲偼廫偺埵偑(4,4)偺慻傒崌傢偣偩偲
愮偺埵偺悢偵4傪巊偊側偄偙偲偵側偭偰偟傑偆丅
傛偭偰廫偺埵偺悢偼(D,Y)偲偟偰(3,5), (5,3)偺偳偪傜偐偱
丂丂(D,Y)=(3,5)偺応崌偼(B,W)=(5,4)
丂丂(D,Y)=(5,3)偺応崌偼(B,W)=(4,5)
堦枩偺埵偺榓偑7偲偄偆偙偲偼丂A+V=7
偙傟傪枮偨偡A偲V偺慻傒崌傢偣偼
(A,V)偲偟偰丂(2,5), (3,4), (4,3), (5,2)
昐偺埵偺悢偵擇恖偲傕2傪巊偭偰偄傞偺偱
(2,5) (5,2)偺慻傒崌傢偣偼柍棟丅
傛偭偰堦枩偺埵偺悢偼(A,V)偲偟偰(3,4), (4,3)偺偳偪傜偐偱
丂丂(D,Y)=(3,5)妿偮(B,W)=(5,4)偺応崌偼(A,V)=(4,3)
丂丂(D,Y)=(5,3)妿偮(B,W)=(4,5)偺応崌偼(A,V)=(3,4)
埲忋偐傜
丂丂(A,B,C,D,E) = (3,4,2,5,1) 偺帪(V,W,X,Y,Z)= (4,5,2,3,1)
丂丂(A,B,C,D,E) = (4,5,2,3,1) 偺帪(V,W,X,Y,Z)= (3,4,2,5,1)
傛偭偰擇恖偑嶌偭偨悢偼丄45231丄34251
(3)
懢榊偺嶌偭偨5寘偺悢傪丂ABCDE
壴巕偺嶌偭偨5寘偺悢傪丂VWXYZ 偲偡傞丅
(2)偺(偁)偱愢柧偟偨偲偍傝丄
擇恖偑嶌偭偨悢偺榓偵0偑偁傟偽
偦偺埵偺悢偵梡偄偨偺偼擇恖偲傕5偱偁傞丅
崱夞偼廫偺埵偺悢偺榓偵0偑偁傞偺偱
丂丂(D,Y) = (5,5)
偙傟傪摜傑偊偰懠偺埵偵梡偄偨悢傪峫偊傞丅
堦偺埵偺悢偺榓偑6偱偁傞偲尵偆偙偲偼丂E+Z=6丂
偙傟傪枮偨偡E偲Z偺慻傒崌傢偣偼
(E,Z) 偲偟偰 (2,4), (3,3), (4,2)
昐偺埵偺悢偺榓偑5偲偄偆偙偲偼 C+X+1=5
(廫偺埵偺孞忋傝偑偁傞偺偱)
偙傟傪枮偨偡C偲X偺慻傒崌傢偣偼
(C,X)偲偟偰丂(1,3), (2,2), (3,1)
(E,Z)=(2,4)偺応崌偼(C,X)= (1,3), (3,1)
(E,Z)=(3,3)偺応崌偼(C,X)= (2,2)
(E,Z)=(4,2)偺応崌偼(C,X)= (1,3), (3,1)
愮偺埵偺悢偺榓偑偲偄偆偙偲偼丂B+W=7
偙傟傪枮偨偡B偲W偺慻傒崌傢偣偼
(B,W)偲偟偰丂(3,4), (4,3)丅
偲偄偆偙偲偼堦偺埵偑(3,3)偺慻傒崌傢偣偩偲
愮偺埵偺悢偵3傪巊偊側偄偙偲偵側偭偰偟傑偆丅
傛偭偰堦偺埵偺悢偼(E,Z)偲偟偰(2,4), (4,2)偺偳偪傜偐偱偁傞丅
(E,Z)=(2,4)妿偮(C,X)=(1,3)丒丒丒W偵3傕4傕巊偊側偄偺偱偙偺慻傒崌傢偣偼柍棟丅
(E,Z)=(2,4)妿偮(C,X)=(3,1)偺応崌偼(B,W)=(4,3)
(E,Z)=(4,2)妿偮(C,X)=(1,3)偺応崌偼(B,W)=(3,4)
(E,Z)=(4,2)妿偮(C,X)=(3,1)丒丒丒B偵3傕4傕巊偊側偄偺偱偙偺慻傒崌傢偣偼柍棟丅
堦枩偺埵偺榓偑3偲偄偆偙偲偼丂A+V=3
偙傟傪枮偨偡A偲V偺慻傒崌傢偣偼
(A,V)偲偟偰丂(1,2) (2,1)丅
(E,Z)=(2,4)妿偮(C,X)=(3,1)妿偮(B,W)=(4,3)偺応崌偼(A,V)=(1,2)
(E,Z)=(4,2)妿偮(C,X)=(1,3)妿偮(B,W)=(3,4)偺応崌偼(A,V)=(2,1)
丂丂(A,B,C,D,E) = 14352 偺帪(V,W,X,Y,Z)= 23154
丂丂(A,B,C,D,E) = 23154 偺帪(V,W,X,Y,Z)= 14352
傛偭偰擇恖偑嶌偭偨悢偼丄14352丄23154
(4)
擇恖偺嶌偭偨悢偺嵎偑惓悢側偺偱
擇恖偺嶌偭偨悢偺偆偪丄戝偒偄曽偐傜彫偝偄曽傪堷偄偨偙偲偵側傞丅
崱夞偼
擇恖偺嶌偭偨悢偺偆偪戝偒偄曽傪丂ABCDE
擇恖偺嶌偭偨悢偺偆偪彫偝偄曽傪丂VWXYZ 偲偡傞丅
堦偺埵偺悢偺嵎偑0偱偁傞偲尵偆偙偲偼丂E-Z=0丂
偙傟傪枮偨偡E偲Z偺慻傒崌傢偣偼
(E,Z) 偲偟偰 (1,1), (2,2), (3,3), (4,4), (5,5)
廫偺埵偺悢偺嵎偑2偲偄偆偙偲偼 D-Y=2
偙傟傪枮偨偡D偲Y偺慻傒崌傢偣偼
(D,Y)偲偟偰丂(3,1), (4,2), (5,3)
昐偺埵偺悢偺嵎偑8偲偄偆偙偲偼
孞傝壓偘偺偁傞寁嶼傪偡傞偙偲偵側傞丅
(孞傝壓偘側偟偩偲嵟彫偱傕9-1=8側偺偱)
偲側傞偲
(C,X)偲偟偰(1,3), (2,4), (3,5)偺偳傟偐偲偄偆偙偲偵側傞丅
愮偺埵偺悢偺嵎偑5偲偄偆偙偲偼
偙傟傕孞傝壓偘側偟偱偼弌棃側偄丅
(孞傝壓偘側偟偩偲嵟彫偱傕6-1=5側偺偱)
昐偺埵偺偲偙傠偱孞傝壓偘偑偁傞偙偲傕摜傑偊傞偲
(B,W) 偲偟偰丂(1,5)偺傒丅
偲側傞偲丄(C,X)=(1,3), (3,5)偼摉偰偼傑傜側偄偙偲偵側傞偺偱 (C,X) = (2,4)
偙偺偙偲偐傜(E,Z)=(1,1), (2,2), (4,4), (5,5)偼摉偰偼傑傜側偄偙偲偵側傞丅
傛偭偰(E,Z) = (3,3)
偝傜偵偙偺偙偲偐傜(D,Y)= (3,1), (5,3)傕摉偰偼傑傜側偄偙偲偵側傞丅
傛偭偰(D,Y)=(4,2)
偙偙傑偱傪傑偲傔傞偲
丂丂(E,Z) = (3,3)
丂丂(D,Y) = (4,2)
丂丂(C,X) = (2,4)
丂丂(B,W) = (1,5)
偟偐偁傝偊側偄偙偲偵側傞偺偱昁慠揑偵
丂丂(A,V) = (5,1)
傛偭偰
丂丂(A,B,C,D,E) = (5,1,2,4,3)
丂丂(V,W,X,Y,Z) = (1,5,4,2,3)
擇恖偺嶌偭偨悢偼丄51243丄
15423
夝摎丒偦偺19
乮儁儞僱亅儉丗teki乯
侾丂俆係侾俁俀丂乮俆係俁俀侾丄俆係俁侾俀丄俆係俀俁侾丄俆係俀侾俁丄俆係侾俁俀偺弴偱偡丅乯
俀丂偁丂侾偐傜俆傑偱偟偐悢帤偑側偄偺偱丄寘偑孞傝忋偑傞偺偼俆亄俆偺帪偩偗偱偡丅
偙偺帪丄昁偢榓偺拞偺悢偵偼侽偑尰傟傑偡丅
榓偺俈俋係俉俀偵偼丄侽偑側偄偺偱丄寘偺孞傝忋偑傝偼惗偠偰偄傑偣傫丅
丂丂偄丂係俆俀俁侾丄俁係俀俆侾乮寘忋偑傝偑側偄偺偱丄侾偺埵偼侾亄侾丄昐偺埵偼俀亄俀丄
愮偺埵偼俆亄係偱偡丅屻偼揔摉偵摉偰偼傔傟偽偱偒傑偡偹丅乯
俁丂俀俁侾俆係丄侾係俁俆俀
係丂俆侾俀係俁丄侾俆係俀俁
夝摎丒偦偺20
乮儁儞僱亅儉丗怴攐恖悷挬乯
(1)戝偒偄曽偐傜丄54321,54312,54231,54213,54132ゥ艂爞閭﹤鐏A
戝偒偄傎偆偐傜俆斣栚偺悢偼丄54132
(2)(偁)奺寘偺榓偼丄俀乣侾侽偺抣偲側傞偑丄79482偵偼侽偑側偄偺偱偔傝忋偑傝偼側偄丅
(偄)
| 巵柤 | 枩 | 愮 | 昐 | 廫 | 堦 |
|---|---|---|---|---|---|
| 懢榊 | A | B | C | D | E |
| 壴巕 | F | G | H | I | J |
| 榓 | 7 | 9 | 4 | 8 | 2 |
丂丂堦偺埵丂榓偑2傛傝丄(E,J)=(1,1)
丂丂廫偺埵丂榓偑8傛傝丄(D,I)=(3,5)丄(4,4)丄(5,3)
丂丂昐偺埵丂榓偑4傛傝丄(C,H)=(1,3)丄(2,2)丄(3,1)
丂丂愮偺埵丂榓偑9傛傝丄(B,G)=(4,5)丄(5,4)
丂丂枩偺埵丂榓偑7傛傝丄(A,F)=(2,5)丄(3,4)丄(4,3)丄(5,2)
偙傟傛傝丂堦偺埵偑寛掕偟丄師偵昐偺埵偑寛掕
丂丂堦偺埵丂榓偑2傛傝丄(E,J)=(1,1)
丂丂廫偺埵丂榓偑8傛傝丄(D,I)=(3,5)丄(4,4)丄(5,3)
丂丂昐偺埵丂榓偑4傛傝丄(C,H)=(2,2)
丂丂愮偺埵丂榓偑9傛傝丄(B,G)=(4,5)丄(5,4)
丂丂枩偺埵丂榓偑7傛傝丄(A,F)=(2,5)丄(3,4)丄(4,3)丄(5,2)
昐偺埵偺悢偵傛傝丄枩偺埵偺悢偑丄(A,F)=(3,4)丄(4,3)偵峣傜傟傞丅 偙傟偵傛傝廫偺埵偺悢丄(D,I)=(3,5)丄(5,3)偺偄偢傟偐偲側傞丅
丂丂堦偺埵丂榓偑2傛傝丄(E,J)=(1,1)
丂丂廫偺埵丂榓偑8傛傝丄(D,I)=(3,5)丄(5,3)
丂丂昐偺埵丂榓偑4傛傝丄(C,H)=(2,2)
丂丂愮偺埵丂榓偑9傛傝丄(B,G)=(4,5)丄(5,4)
丂丂枩偺埵丂榓偑7傛傝丄(A,F)=(3,4)丄(4,3)
偙偙偱丄(D,I)=(3,5)偲偡傞偲丄(B,G)=(5,4)丄(A,F)=(4,3)偲側傞丅
傑偨丄(D,I)=(5,3)偲偡傞偲丄(B,G)=(4,5)丄(A,F)=(3,4)偲側傞丅
偟偨偑偭偰丄俀偮偺悢偼丄45231偲34251偱偁傞丅
(3)
| 巵柤 | 枩 | 愮 | 昐 | 廫 | 堦 |
|---|---|---|---|---|---|
| 懢榊 | A | B | C | D | E |
| 壴巕 | F | G | H | I | J |
| 榓 | 3 | 7 | 5 | 0 | 6 |
廫偺埵偑0傛傝丄乮D,I)=(5,5)偲側傞丅偔傝忋偑傝偑1偁傞偺偱丄C+H=4
偙傟埲奜偵孞傝忋偑傝偼側偄丅5埲奜偺悢帤傪梡偄偰丄
丂丂堦偺埵丂榓偑6傛傝丄(E,J)=(2,4)丄(3,3)丄(4,2)
丂丂昐偺埵丂榓偑4傛傝丄(C,H)=(1,3)丄(2,2)丄(3,1)
丂丂愮偺埵丂榓偑7傛傝丄(B,G)=(3,4)丄(4,3)
丂丂枩偺埵丂榓偑3傛傝丄(A,F)=(1,2)丄(2,1)
偙偙偱丄(A,F)=(1,2)偲偡傞偲丄(C,H)=(3,1)丄(B,G)=(4,3)丄 (E,J)=(2,4)偲側傞丅
傑偨丄(A,F)=(2,1)偲偡傞偲丄(C,H)=(1,3)丄(A,F)=(2,1)丄 (E,J)=(4,2)偲側傞丅
偟偨偑偭偰丄俀偮偺悢偼丄14352偲23154偱偁傞丅
(4)
| 巵柤 | 枩 | 愮 | 昐 | 廫 | 堦 |
|---|---|---|---|---|---|
| 懢榊 | A | B | C | D | E |
| 壴巕 | F | G | H | I | J |
| 嵎 | 3 | 5 | 8 | 2 | 0 |
(懢榊偺俆寘偺惍悢)亜(壴巕偺俆寘偺惍悢)偲偡傞丅
奺埵孞傝壓偑傝偑側偄偲偡傟偽丄偦偺悢偼4,3,2,1,0偲側傞偺偱丄 愮偺埵偺5偲昐偺埵偺8偼孞傝壓偑傝偑昁梫側悢帤偱偁傞丅
偟偨偑偭偰丄A-F=4,乮B+10)-G=6,(C+10)-H=8偑昁梫偱偁傞丅
傛偭偰丄乮A,F)=(5,1)丄乮B,G)=(1,5)丄乮C,H)=(2,4)偲側傞丅
堦偺埵偼巆傝偺悢帤傛傝丄(E,J)=(3,3)偲側傝丄 廫偺埵偼丄(D,I)=(4,2)偲寛掕偱偒傞丅
偟偨偑偭偰丄 俀偮偺悢偼51243偲15423偱偁傞丅
夝摎丒偦偺21
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮侾乯俆斣栚偵戝偒側悢帪偼俆係侾俁俀偱偡丅
乮俀乯乮偁乯偦偺侾丄
丂丂丂俈俋係俉俀偺悢帤傪墶偵壛嶼偟傑偡丅俈亄俋亄係亄俉亄俀亖俁侽偱偡丅
丂丂丂僇乕僪偺悢帤偼乮侾亄俀亄俁亄係亄俆乯亊俀亖俁侽偲側傝傑偡丅
丂丂丂廬偭偰悢帤偑堦抳偟偰偄傞偺偱孞傝忋偑傝偑側偐偭偨偲敾抐偟傑偡丅
丂丂丂偦偺俀丄
丂丂丂2恖偺悢帤偱孞傝忋偑傞悢帤偼俆偲俆傪壛嶼偟侾侽偵側偭偨帪偱偡偑悢帤偺拞偵侽偑偁傝傑偣傫丄廬偭偰孞傝忋偑傝偑側偐偭偨偲敾抐偟傑偡丅
丂丂乮偄乯懢榊偝傫偼俁係俀俆侾偱壴巕偝傫偼係俆俀俁侾偱偡丅
乮俁乯懢榊偝傫偼侾係俁俆俀偱壴巕偝傫偼俀俁侾俆係偱偡丅
乮係乯懢榊偝傫偼俆侾俀係俁偱壴巕偝傫偼侾俆係俀俁偱偡丅
夝摎丒偦偺22
乮儁儞僱亅儉丗僸儍僋儗儞丒儔儔儞僕儍乯
(1)
摎丗俆係侾俁俀
夝朄丗戝偒偄傎偆偐傜弴偵丄師偺傛偆偵側傞偨傔丅
俆係俁俀侾丄俆係俁侾俀丄俆係俀俁侾丄俆係俀侾俁丄俆係侾俁俀
(2)乮偁乯
偔傝忋偑傝偑側偐偭偨棟桼偼丄奺埵偺悢帤偺榓偑俁侽偵側偭偰偄傞偨傔丅
懢榊偝傫偺嶌偭偨俆偗偨偺悢帤偺奺埵偺悢帤偺榓偼侾俆偱丄壴巕偝傫傕摨條偵侾俆偵側傞丅
偔傝忋偑傝偑偁偭偨傜丄俁侽偵側傜側偄偱丄傕偭偲彮側偔側傞丅
乮偄乯
摎丗俁係俀俆侾偲係俆俀俁侾
夝朄丗
丂丂俙俛俠俢俤
丂亄俥俧俫俬俰
劒劒劒劒劒劒
丂丂俈俋係俉俀
偙偺偲偒丄俤亖俰亖侾丄俠亖俫亖俀 偼柧傜偐丅
俛偲俧偼丄係偲俆側偺偱丄俢偲俬偼丄俆偲俁偵側傝丄俙偲俥偼丄俁偲係偵寛傑傞丅
(3)
摎丗俀俁侾俆係偲侾係俁俆俀
夝朄丗
丂丂俙俛俠俢俤
丂亄俥俧俫俬俰
劒劒劒劒劒劒
丂丂俁俈俆侽俇
偙偙偱丄俢亖俬亖俆偵側傞偺偱丄俛偲俧偼丄俁偲係偵側傝丄
俤偲俰偼丄係偲俀偵側傞丅巆傝偺悢帤傪峫偊傞偲丄
俙亖俀丆俥亖侾偑寛傑傝丄俠亖侾丆俫亖俁偲側傞丅
(4)
摎丗俆侾俀係俁偲侾俆係俀俁
夝朄丗
丂丂俙俛俠俢俤
丂亅俥俧俫俬俰
劒劒劒劒劒劒
丂丂俁俆俉俀侽
俆偲俉偺摎偵側傞偲偙傠偵丄偔傝壓偑傝偑峫偊傜傟傞丅
偟偨偑偭偰丄俛亖侾丆俧亖俆偑寛傑傞丅偡傞偲丄俙亖俆丆俥亖侾偵側傝丄
俠亖俀丆俫亖係偲側傞丅俤亖俰側偺偱丄俤亖俰亖俁偵側傝丄
俢亖係丆俬亖俀偑寛傑傞丅
夝摎丒偦偺23
乮儁儞僱亅儉丗傑偡傑偡僞僐偝傫乯
夝摎丗丂乮侾乯丂俆係侾俁俀
乮俀乯丂乮偁乯丂俆偮偺悢帤偺榓偑俁侽偩偐傜丂乮丠乯
乮俀乯丂乮偄乯丂俁係俀俆侾丂偲丂係俆俀俁侾
乮俁乯丂侾係俁俆俀丂偲丂俀俁侾俆係
乮係乯丂俆侾俀係俁丂偲丂侾俆係俀俁
夁掱丗
乮侾乯丂偙傟偼丄堦斣戝偒側悢帤偐傜偐偧偊偰偄偒傑偟偨丅
堦斣戝偒側悢帤偼嵍偐傜戝偒偄悢帤偐傜暲傋偨丄乽俆係俁俀侾乿偱偡丅
弴偵丄俆係俁侾俀丄俆係俀俁侾丄俆係俀侾俁丄俆係侾俁俀丄丒丒丒偱丄
俆斣栚偵戝偒側悢帤偼乽俆係侾俁俀乿偱偡丅
乮俀乯乮偁乯丂侾乣俆偺俆枃偺僇乕僪傪巊偆傢偗偱偡偐傜丄
乽俆寘偺悢帤乿偺俆偮偺悢帤偺崌寁偼丄乽侾俆乿偱偡丅
傆偨傝偑乽俆寘偺悢帤乿傪偮偔傞栿偱偡偐傜丄
侾俆亄侾俆丂偱丄乽俁侽乿偱偡丅
偮傑傝丄孞傝忋偑傝偑側偗傟偽丄俀偮偺乽俆寘偺悢帤乿偺榓傪峔惉偡傞悢帤偺榓偼乽俁侽乿
偵側傞偼偢偱偡丅
傕偟丄孞傝忋偑傝偑偁傞偲偡傟偽丄擇恖偑摨偠寘偵乽俆乿傪擖傟偨帪偩偗偱偡丅
俀偮偺乽俆寘偺悢帤乿偺榓傪峔惉偡傞悢帤偺榓偼乽俀侾乿偵側傝傑偡丅
乮俀乯乮偄乯丂傑偢丄堦偺埵丅榓偑丂俀丂偱偡偐傜丄侾亄侾偟偐偁傝傑偣傫丅
丂丂丂仺丂XXXX1丂亄丂XXXX1
愮偺埵丅榓偑俋偱偡偐傜丄俆亄係偟偐偁傝傑偣傫丅
丂丂丂仺丂X俆XX侾丂亄丂X係XX1
昐偺埵丅榓偑係偱丄侾亄俁丂偼丄堦偺埵偱丂侾丂巊偭偰偄傞偺偱丄
俀亄俀丂偟偐偁傝傑偣傫丅
丂丂丂仺丂X俆俀X侾丂亄丂X係俀X侾
枩偺埵丅榓偑俈偱丄丂俀亄俆丂偼丄昐偺埵偱丂俀傪巊偭偰偄傞偺偱丄俁亄係偟偐偁傝傑偣傫丅
係丂偼偙偙偱尵偆乽亄乿偺偁偲丄屻崁偵巊偭偰偄傞偺偱丄慜崁偵擖傟傑偡丅
丂丂丂仺丂係俆俀X侾丂亄丂俁係俀X侾
巆偭偨悢帤傪廫偺埵偵偄傟傑偡丅
丂丂丂仺丂係俆俀俁侾丂亄丂俁係俀俆侾丂乮亖俈俋係俉俀乯
乮俁乯廫偺埵丅榓偑侽偱偡偐傜丄俆亄俆偟偐偁傝傑偣傫丅
乮堦偺埵偺孞傝忋偑傝偼桳傝摼傑偣傫丅侾乣俆偺俀悢偺榓偑侾俇偵偼側傝摼側偄偐傜偱偡丅乯
丂丂丂仺丂XXX俆X丂亄丂XXX俆X
枩偺埵丅榓偑俁丂偡偐傜丄侾亄俀偟偐偁傝傑偣傫丅
丂丂丂仺丂侾XX俆X丂亄丂俀XX俆X
昐偺埵丅廫偺埵偺孞傝忋偑傝傪峫椂偟偰丄榓偑係偵側傜側偗傟偽偄偗傑偣傫丅
枩偺埵偱堦曽偑丂俀丂傪巊偭偰偄傞偺偱丄俀亄俀偼巊偊傑偣傫丅丂
侾亄俁丂偵側傝傑偡偑丄慜崁偑枩偺埵偱侾傪巊偭偰偄傑偡丅
丂丂丂仺丂侾X俁俆X丂亄丂俀X侾俆X
愮偺埵丅榓偑丂俈丂偱丄俆偼廫偺埵偱巊偭偰偄傞偺偱丄俁亄係偟偐偁傝傑偣傫丅丂
俁丂偼慜崁偵擖偭偰偄傞偺偱丄屻崁偵擖傟傑偡丅
丂丂丂仺丂侾係俁俆X丂亄丂俀俁侾俆X
巆偭偨悢帤傪堦偺埵偵擖傟傑偡丅
丂丂丂仺丂侾係俁俆俀丂亄丂俀俁侾俆係丂乮亖俁俈俆侽俇乯
乮係乯丂傑偢丄愮偺埵丄昐偺埵偱丄孞傝壓偑傝偑偁傝傑偡丅
乮孞傝壓偘側偄偲丄丂俉丂偲丂俆丂偵偼側傝摼傑偣傫丅乯
愮偺埵丅嵎偑丂俆丂偵側傞偺偼丄昐偺埵偺孞傝壓偘傕峫椂偟偰丄侾侾亅俆偟偐偁傝傑偣傫丅
丂丂丂仺丂X侾XXX丂亅丂X俆XXX
昐偺埵丅嵎偑丂俉丂偵側傞偺偼丄丂侾侾亅俁丄侾俀亅係丄侾俁亅俆偱偡丅
愮偺埵偱慜崁偵丂侾丂丄屻崁偵丂俆丂傪巊偭偰偄傞偺偱丄侾俀亅係偟偐偁傝傑偣傫丅
丂丂丂仺丂X侾俀XX丂亅丂X俆係XX
枩偺埵丅嵎偑丂俁丂偵側傞偺偼丄愮偺埵偺孞傝壓偘傕峫椂偟偰丄俆亅侾偟偐偁傝傑偣傫丅
丂丂丂仺丂俆侾俀XX丂亅丂侾俆係XX
堦偺埵丅嵎偑丂侽丂偵側傞偺偼丄巆偭偰偄傞悢帤偱丄俁亅俁偩偗偱偡丅
丂丂丂仺丂俆侾俀X俁丂亅丂侾俆係X俁
巆偭偨悢帤傪廫偺埵偵擖傟傑偡丅
丂丂丂仺丂俆侾俀係俁丂亅丂侾俆係俀俁丂乮亖俁俆俉俀侽乯
夝摎丒偦偺24
乮儁儞僱亅儉丗T_Tatekawa乯
(1)
枩偺埵偵 5 傪抲偒傑偡丏1-4 偺暲傋曽偼 4!=24 捠傝偁傞偺偱丆5斣栚偵
戝偒側悢偺枩偺埵偼 5 偱偡丏
師偵愮偺埵偵 4 傪抲偒傑偡丏1-3 偺暲傋曽偼 3!=6 捠傝偁傞偺偱丆5斣栚偵
戝偒側悢偺愮偺埵偼 4 偱偡丏
屻偼 1-3 偺暲傋懼偊偱偡丏
戝偒偄弴偵 321, 312, 231, 213, 132, 123 偲側傞偺偱丆5斣栚偵戝偒側悢偼
54132 偱偡丏
(2) 乮偁乯
1 偐傜 5 傑偱傪懌偟忋偘傞偲 15 偱偡丏
擇恖偑偦傟偧傟巊偆僇乕僪偺悢偺榓偼 30 偵側傝傑偡丏
堦曽丆
丂丂丂7+9+4+8+2 = 30
偱偡丏孞傝忋偑傝偑偁傟偽丆孞傝忋偑傝堦夞偛偲偵奺寘偺悢偺榓偑
10 - 1 = 9 偢偮彮側偔側傝傑偡丏
偙偺偨傔丆擇恖偑嶌偭偨悢偺榓偑 30 側傜偽丆孞傝忋偑傝偑側偐偭偨
帠偺側傝傑偡丏
乮偄乯
2=1+1, 9=4+5 偱偡丏
懢榊偝傫偑嶌偭偨悢偵傑偢 1 偲 5 偑娷傑傟丆
壴巕偝傫偑嶌偭偨悢偵 1 偲 4 偑娷傑傟傞偲偟傑偡丏
廫偺埵偺 8 傪嶌傞偵偼 8=5+3 偱偡丏
5 偼懢榊偝傫偑婛偵巊偭偰偄傞偺偱丆壴巕偝傫偑巊偄傑偡丏
3 偼懢榊偝傫偑巊偄傑偡丏
枩偺埵偺 7 傪嶌傞偵偼丆7=4+3 偱偡丏
4 偼壴巕偝傫偑婛偵巊偭偰偄傞偺偱懢榊偝傫偑丆
3 偼懢榊偝傫偑婛偵巊偭偰偄傞偺偱壴巕偝傫偑巊偄傑偡丏
昐偺埵偺 4 傪嶌傞偵偼丆4=2+2 偱偡偺偱丆擇恖偑巊偄傑偡丏
埲忋偐傜擇恖偑嶌偭偨悢偼 45231 偲 34251 偱偡丏
(3) 3+7+5+0+6=21 側偺偱丆孞傝忋偑傝偑1夞偁傝傑偡丏
1 偐傜 5 傑偱偺擇偮偺悢傪巊偭偨榓偺嵟戝偼 10 側偺偱丆
廫偺埵偱孞傝忋偑傝偑婲偒偨帠偑暘偐傝傑偡丏10=5+5 傛傝丆
擇恖偑嶌偭偨悢偺廫偺埵偼丆偳偪傜傕 5 偱偡丏
枩偺埵偺 3 傪嶌傞偵偼丆3=2+1 偱偡偺偱丆懢榊偝傫偑 2 傪丆
壴巕偝傫偑 1 傪巊偆帠偵偟傑偡丏
愮偺埵偺 7 傪嶌傞偵偼丆7=4+3 偱偡丏偙偙偼屻偱峫偊傑偡丏
堦偺埵偺 6 傪嶌傞偵偼丆6=4+2 偱偡丏懢榊偝傫偼婛偵 2 傪
巊偭偰偄傞偺偱 4 傪巊偄傑偡丏壴巕偝傫偼 2 傪巊偄傑偡丏
愮偺埵傪傕偆堦搙峫偊傞偲丆懢榊偝傫偑巊偊傞偺偼 3 偱偡丏
壴巕偝傫偼 4 傪巊偄傑偡丏
昐偺埵偼孞傝忋偑傝傪彍偔偲 4=3+1 偲側傝傑偡丏懢榊偝傫偑
1 傪丆壴巕偝傫偑 3 傪巊偄傑偡丏
埲忋偐傜擇恖偑嶌偭偨悢偼 23154 偲 14352 偱偡丏
(4) 傑偢昐偺埵偵拲栚偟傑偡丏1 偐傜 5 偺悢傪巊偭偨堷偒嶼偱丆
戝偒側悢偐傜彫偝偄悢傪堷偄偨偲偒丆嵟戝偲側傞偺偼
5-1 = 4 偱偡丏
偙偺偨傔丆昐偺埵偱偼乽彫偝偄悢偐傜戝偒側悢傪堷偔乿帠偑
婲偒偰偄偰丆愮偺埵偐傜1傪帩偭偰偒偰偄傑偡丏
摨條偵愮偺埵傕丆枩偺埵偐傜 1 傪帩偭偰偒偰偄傑偡丏
枩偺埵偺 2 偮偺悢偺嵎偼 4 偵側傞偺偱丆堷偐傟傞悢偺枩偺
埵偑 5丆堷偔悢偺枩偺埵偑 1 偲側傞偙偲偑傢偐傝傑偡丏
師偵愮偺埵傪峫偊傑偡偲丆杮棃偼 6 偵側傞偲偙傠偑丆昐偺
埵偵帩偭偰偄偐傟偰 5 偵側偭偰偄傞傢偗偱偡丏嵎偑 6 偵
側傞慻傒崌傢偣偼
10+1-5 = 6 偟偐側偄偺偱丆堷偐傟傞悢偺愮偺埵偑 1丆堷偔悢偺
愮偺埵偑 5 偲側傞偙偲偑傢偐傝傑偡丏
偙偺帪揰偱巊偭偰偄側偄僇乕僪偼偳偪傜偺悢傕 2, 3, 4 偱偡丏
廫偺埵偵偮偄偰 4-2=2 側偺偱丆堷偐傟傞悢偺廫偺埵偑 4丆堷偔
悢偺廫偺埵偑 2 偲側傞偙偲偑傢偐傝傑偡丏
堦偺埵偼嵎偑 0 側偺偱丆擇偮偺悢偺堦偺埵偑摨偠帠偵側傝傑偡丏
傛偭偰 3 偱偡丏
巆偭偨昐偺埵偼丆堷偐傟傞悢偺昐偺埵偑 2丆堷偔悢偺昐偺埵偑
4 偱偡丏
埲忋偐傜擇恖偑嶌偭偨悢偼 51243 偲 15423 偱偡丏
夝摎丒偦偺25
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
(1)乽54***乿 偲偄偆僷僞乕儞偺悢偼丄3両亖6 捠傝偁傝傑偡丅
嬶懱揑偵彂偒弌偡偲丄戝偒偄弴偵
丂丂丂54321丄54312丄54231丄54213丄54132丄54123
偩偐傜5斣栚偵戝偒側悢偼丄54132偱偡丅
(2)
(偁)榓偺悢偵偮偄偰奺埵偺悢帤傪崌寁偡傞偲丄偔傝忋偑傝偑側偄応崌偼 30 偵側傝傑偡丅
丂丂丂2亊(1+2+3+4+5)亖30
偔傝忋偑傝偑堦夞偁傞偲丄10恑朄偱悢傪昞偟偰偄傞偺偱丄
偦偺寘偼 10 尭傝丄1偮忋偺寘偼1憹偊傞偺偱 21 偵側傝傑偡丅
丂丂丂30-10+1亖21
乽79482乿偺奺埵偺悢偺榓偼丄30 側偺偱偔傝忋偑傝偼側偐偭偨偲峫偊傜傟傑偡丅
(偄)丂榓偺昞(乽1乿偺埵偺昞乯
| 丂 | 侾 | 俀 | 俁 | 係 | 俆 |
|---|---|---|---|---|---|
| 侾 | 俀 | 俁 | 係 | 俆 | 俇 |
| 俀 | 俁 | 係 | 俆 | 俇 | 俈 |
| 俁 | 係 | 俆 | 俇 | 俈 | 俉 |
| 係 | 俆 | 俇 | 俈 | 俉 | 俋 |
| 俆 | 俇 | 俈 | 俉 | 俋 | 侽 |
乽79482乿偵偮偄偰丄
(1)堦偺埵偼丄乽1乿偲乽1乿偱偡丅
(2)愮偺埵偼丄乽4乿偲乽5乿偱偡丅
(3)廫偺埵偼丄(2)偱乽4乿傪侾偮巊偭偰偟傑偭偨偺偱丄乽5乿偲乽3乿偱偡丅
(4)枩偺埵偼丄(2)偲(3)偱乽5乿傪俀偮偲傕巊偭偰偟傑偭偨偺偱丄乽3乿偲乽4乿偱偡丅
(5)昐偺埵偼丄巆傝偺乽2乿偲乽2乿偱偡丅
傑偲傔傞偲丄乽34251乿偲乽45231乿偱偡丅
(3)乽37506乿偼丄奺埵偺悢帤偺榓偑 21 側偺偱偔傝忋偑傝偑丄堦夞偁傝傑偡丅
(1)廫偺埵偼丄乽5乿偲乽5乿偱偡丅
(2)愮偺埵偼丄乽3乿偲乽4乿偱偡丅
(3)堦偺埵偼丄乽4乿偲乽2乿偱偡丅
(4)枩偺埵偼丄乽2乿偲乽1乿偱偡丅
(5)昐偺埵偼丄廫偺埵偐傜(1)偔傝忋偑傝偑偁傞偺偱丄乽1乿偲乽3乿偱偡丅
傑偲傔傞偲丄乽23154乿偲乽14352乿偱偡丅
(4)嵎偺悢偵偮偄偰奺埵偺悢帤偺榓偼丄堦夞偔傝壓偑傝偑偁傞偲丄
偦偺寘偼 10 憹偊丄1偮忋偺寘偼1尭傞偺偱 9 偵側傝傑偡丅
丂丂丂(1+2+3+4+5)-(1+2+3+4+5)+10-1亖9
擇夞偔傝壓偑傝偑偁傞偲丄18 偵側傝傑偡丅
丂丂丂丂嵎偺昞(嵍偺悢偲忋偺悢偲偺嵎偺乽1乿偺埵偺昞)
| 丂 | 侾 | 俀 | 俁 | 係 | 俆 |
|---|---|---|---|---|---|
| 侾 | 侽 | 俋 | 俉 | 俈 | 俇 |
| 俀 | 侾 | 侽 | 俋 | 俉 | 俈 |
| 俁 | 俀 | 侾 | 侽 | 俋 | 俉 |
| 係 | 俁 | 俀 | 侾 | 侽 | 俋 |
| 俆 | 係 | 俁 | 俀 | 侾 | 侽 |
乽35820乿偼丄奺埵偺悢帤偺榓偑 18 側偺偱丄偔傝壓偑傝偑擇夞偁傝傑偡丅
(1)昞偺拞偵(5)偼弌偰偙側偄偺偱丄愮偺埵偼昐偺埵偵偔傝壓偑傞偙偲傪忦審偵丄乽1乿偲乽5乿偱偡丅
(2)昐偺埵偼丄(1)偱乽1乿偲乽5乿偑弌偰偒偨偺偱丄乽2乿偲乽4乿偱偡丅
(3)堦偺埵偼丄摨偠悢帤偱側偄偲偄偗側偄偺偱丄乽3乿偲乽3乿偱偡丅
(4)廫偺埵偼丄(3)偑傕偆側偄偺偱丄乽4乿偲乽2乿偱偡丅
(5)枩偺埵偼丄愮偺埵偵偔傝壓偑偭偰偄傞偺偱丄乽5乿偲乽1乿偱偡丅
傑偲傔傞偲丄乽51243乿偲乽15423乿偱偡丅
惓夝幰
| 僶儖僞儞惎恖 | nao | To the stars |
| 怴攐恖悷挬 | 忨偺偍偠偝傫 | 僆儎僕 |
| teki | 岼偺柌 | Toru |
| 傑偡傑偡僞僐偝傫 | T_Tatekawa | 偵偟傗傫 |
| 偺偭偙傫 | 僗儌乕僋儅儞 | 僥儗僗偲傾儕僗 |
| 揮埵斀墳 | 僸儍僋儗儞丒儔儔儞僕儍 | 俥倎倳倱俿 |
| 偙傑偭偨僐 | 傑乕傗 | 栭傆偐偟偺偮傜偄偍偠偝傫 |
| kohji | whale | 恀壞偺僒儞僞 |
| 嶰妏掕婯 |
傑偲傔
(2)(偁)偱孞傝忋偑傝偺敾掕偑偁傝傑偡偑丄
偙傟偑億僀儞僩偐側偲巚偄傑偡丅
偄偨偩偄偨夝摎偱偼丄乽5+5=10乿偺乽0乿偑側偄偐傜偲偄偆傕偺傕丄
懡偐偭偨偱偡偹丅偙偺応崌丄巊偭偰偄傞僇乕僪偑1乣5偱偡偐傜丄
偦偆側傝傑偡偹丅
暿側傾僾儘乕僠偲偟偰偼丄
1乣5偺僇乕僪偺崌寁偑15偱偙傟傪俀偮暘懌偡偙偲偵側傝傑偡偑丄
暲傋偰偱偒偨悢79482偺奺寘偺悢偺榓偑30偵側偭偰偄傑偡偐傜丄
孞傝忋偑傝偼側偄偲偄偆偙偲偵側傝傑偡丅
傕偟偔傝忋偑傝偑偁傟偽丄榓偑21偵側傞偼偢偱偡偐傜偹丅
(孞傝忋偑偭偨10偑丄尒偨栚偼侾偲側傞偨傔乯
偙偺峫偊曽偩偲丄1乣5偲偄偆僇乕僪偺悢偵尷掕偝傟傑偣傫丅
(4)偼丄堷偒嶼偺栤戣偱偡偑丄巹偼
丂丂丂倃亄35820亖倄
偲偟偰丄懌偟嶼偱峫偊傑偟偨丅
偙偺応崌偼丄倃,倄偺奺寘偺榓偑偲傕偵15偱丄
35820偺奺寘偺榓偑18偱偁傞偙偲偐傜丄
偙偺懌偟嶼偵偍偄偰丄偔傝忋偑傝偑俀夞偁傞偲偄偆偙偲偑傢偐傝傑偡丅
嵟屻偼僷僘儖偱偡偑丄偙偆偄偆忣曬偑偁傟偽丄
夝摎偵帄傞帪娫抁弅偵側傝傑偡偹丅
傑偨丄尩枾偵偼丄夝摎偺堦堄惈乮偙傟埲奜偵忦審傪枮偨偡慻傒崌傢偣偼側偄乯傪
帵偡昁梫傕偁傝傑偑丄夝摎傪扵偡拞偱丄帵偝傟偰偄傟偽傛偄偲巚偄傑偡丅
 top
top